Magnetotelluric Signal-Noise Identification and Separation Based on ApEn-MSE and StOMP
Abstract
:1. Introduction
2. Methods
2.1. Approximate Entropy (ApEn)
2.2. Sample Entropy (SampEn)
2.3. Multiscale Entropy (MSE)
2.4. Stagewise Orthogonal Matching Pursuit (StOMP)
3. Simulation Analysis
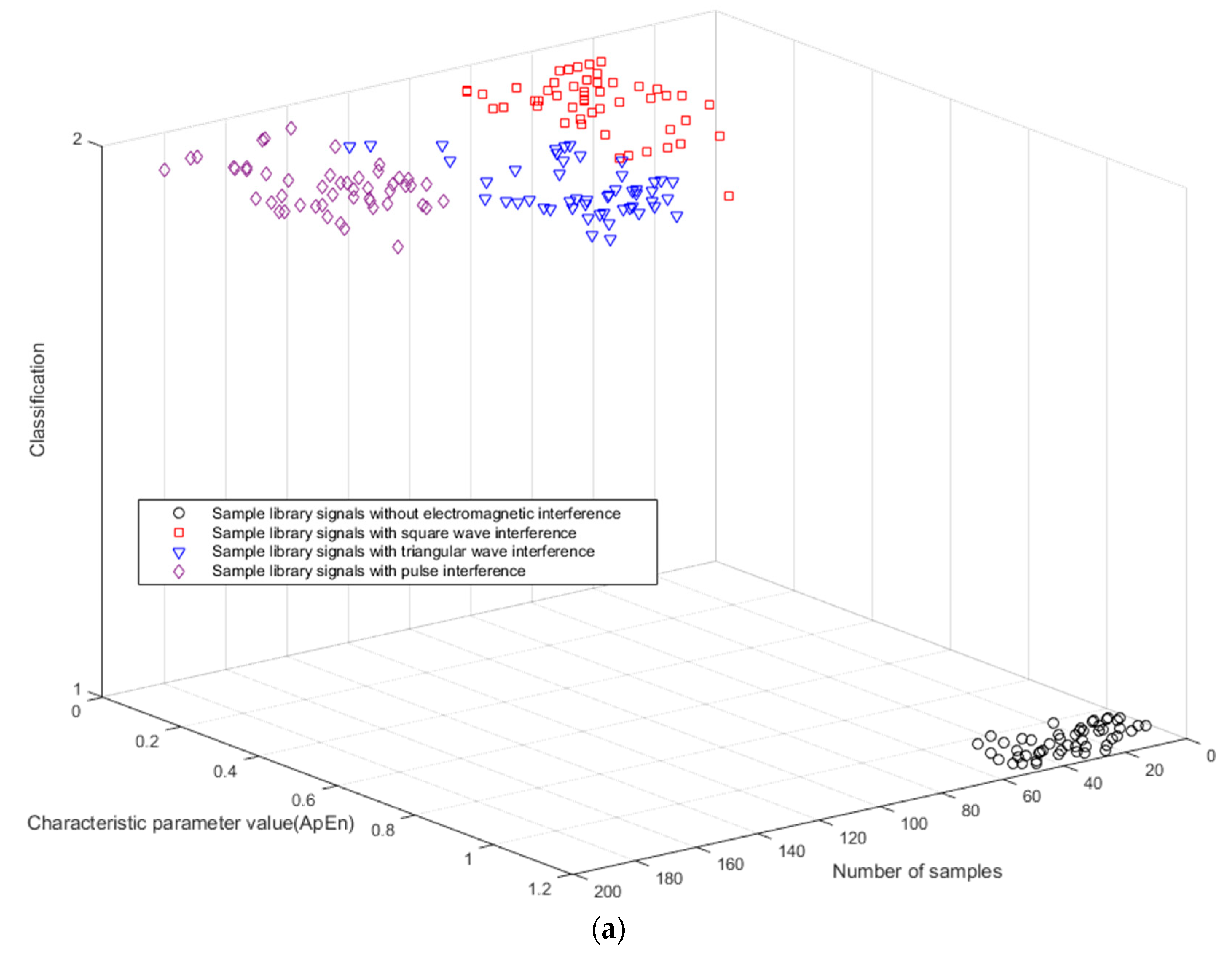
3.1. Sample Library Signals Classification
3.2. Add Artificial Interference to the Test Site Signal
4. Measured Data Analysis
4.1. Time Domain Analysis
4.2. Apparent Resistivity-Phase Curve Analysis
4.3. Polarization Direction Analysis
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cagniard, L. Basic theory of the magnetotelluric method of geophysical prospecting. Geophysics 1953, 18, 605–635. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On determining electrical characteristics of the deep layers of the Earth’s crust. Dokl. Akad. Nauk SSSR 1950, 73, 295–297. [Google Scholar]
- He, L.F.; Chen, L.; Dorji; He, Z.X.; Wang, X.B.; Xiao, B.Y.; Xu, L.G.; Zhao, X.F.; Xi, X.L.; Yao, H.C.; et al. Mapping chromite deposits with audio magnetotellurics in the Luobusa ophiolite of southern Tibet. Geophysics 2018, 83, B47–B57. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Kalscheuer, T.; Greenhalgh, S.; Maurer, H. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modeling. Geophys. J. Int. 2013, 194, 700–718. [Google Scholar] [CrossRef]
- Hennessy, L.; Macnae, J. Source-dependent bias of sferics in magnetotelluric responses. Geophysics 2018, 83, E161–E171. [Google Scholar] [CrossRef]
- Kappler, K.N. A data variance technique for automated despiking of magnetotelluric data with a remote reference. Geophys. Prospect. 2012, 60, 179–191. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Gong, J.Z.; Tang, J.T.; Ren, Z.Y.; Li, G.; Deng, Y.L.; Cai, J. Signal-noise identification of magnetotelluric signals using fractal-entropy and clustering algorithm for targeted de-noising. Fractals 2018, 26, 1840011. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Tang, J.T.; Cai, J.; Liu, X.Q. Audio magnetotelluric signal-noise identification and separation based on multifractal spectrum and matching pursuit. Fractals 2019, 27, 1940007. [Google Scholar] [CrossRef]
- Huang, Z.X. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Karimov, J.; Ozbayoglu, M. Clustering quality improvement of k-means using a hybrid evolutionary model. Procedia Comput. Sci. 2015, 61, 38–45. [Google Scholar] [CrossRef]
- Rahkar Farshi, T.; Demirci, R.; Feiziderakhshi, M.R. Image clustering with optimization algorithms and color space. Entropy 2018, 20, 296. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R.; Amari, S. On clustering histograms with k-Means by Using Mixed α-divergences. Entropy 2014, 16, 3273–3301. [Google Scholar] [CrossRef]
- Wei, M.; Chow, T.W.S.; Chan, R.H.M. Clustering heterogeneous data with k-Means by mutual information-based unsupervised feature transformation. Entropy 2015, 17, 1535–1548. [Google Scholar] [CrossRef]
- Shi, Z.L.; Song, W.Q.; Taheri, S. Improved LMD, permutation entropy and optimized K-Means to fault diagnosis for roller bearings. Entropy 2016, 18, 70. [Google Scholar] [CrossRef]
- Gattone, S.A.; Sanctis, A.D.; Puechmorel, S.; Nicol, F. On the geodesic distance in shapes K-means clustering. Entropy 2018, 20, 647. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Phys. A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Kaplanis, P.A.; Pattichis, C.S.; Zazula, D. Multiscale entropy-based approach to automated surface EMG classification of neuromuscular disorders. Med. Biol. Eng. Comput. 2010, 48, 773–781. [Google Scholar]
- Wu, S.D.; Wu, C.W.; Wu, T.Y.; Wang, C.C. Multi-scale analysis based ball bearing defect diagnostics using Mahalanobis distance and support vector machine. Entropy 2013, 15, 416–433. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Mayer, C.; Bachler, M.; Hörtenhuber, M.; Stocker, C.; Holzinger, A.; Wassertheurer, S. Selection of entropy-measure parameters for knowledge discovery in heart rate variability data. BMC Bioinform. 2014, 15, S2. [Google Scholar] [CrossRef] [Green Version]
- Manis, G.; Aktaruzzaman, M.; Sassi, R. Bubble entropy: An entropy almost free of parameters. IEEE Trans. Biomed. Eng. 2017, 64, 2711–2718. [Google Scholar]
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Donoho, D.L.; Maleki, A.; Motanari, A. Message passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tanner, J. Precise undersampling theorems. Proc. IEEE 2010, 98, 913–924. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.; Montanari, A. Accurate prediction of phase transitions in compressed sensing via a connection to minimax denoising. IEEE Trans. Inf. Theory 2013, 59, 3396–3433. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yan, H.; Tang, J.T.; Zhang, X.; Li, G.; Zhu, H.J. Magnetotelluric noise suppression based on matching pursuit and genetic algorithm. Chin. J. Geophys. 2018, 61, 3086–3101. [Google Scholar]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit. IEEE J. Sel. Top. Signal Process. 2010, 4, 310–316. [Google Scholar] [CrossRef]
- Burioka, N.; Cornelisson, G.; Halberg, F.; Kaplan, D.T.; Suyama, H.; Sako, T.; Shimizu, E.I. Approximate entropy of human respiratory movement during eye-closed waking and different sleep stages. Chest 2003, 123, 80–86. [Google Scholar] [CrossRef]
- Pincus, S. Approximate entropy as an irregularity measure for financial data. Econom. Rev. 2008, 27, 329–362. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Zhou, Y.; Du, S.; Zhang, Y.; Mei, T.; Tian, X. Construction of rules for seizure prediction based on approximate entropy. Clin. Neurophysiol. 2014, 125, 1959–1966. [Google Scholar] [CrossRef]
- Mei, T.; Qiao, J.D.; Zhou, Y.; Gu, H.Y.; Chen, Z.Y.; Tian, X.H.; Gu, K.Y. Analysis of neural oscillations on Drosophila’s subesophageal ganglion based on approximate entropy. Entropy 2015, 17, 6854–6871. [Google Scholar] [CrossRef]
- Manis, G.; Aktaruzzaman, M.; Sassi, R. Low computational cost for sample entropy. Entropy 2018, 20, 61. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J.A.K. Transductive Feature selection using clustering-based sample entropy for temperature prediction in weather forecasting. Entropy 2018, 20, 264. [Google Scholar] [CrossRef]
- Bakhchina, A.V.; Arutyunova, K.R.; Sozinov, A.A.; Demidovsky, A.V.; Alexandrov, Y.I. Sample Entropy of the heart rate reflects properties of the system organization of behaviour. Entropy 2018, 20, 449. [Google Scholar] [CrossRef]
- Ahmadi, S.; Sepehri, N.; Wu, C.; Szturm, T. Sample entropy of human gait center of pressure displacement: A Systematic Methodological Analysis. Entropy 2018, 20, 579. [Google Scholar] [CrossRef]
- McCamley, J.D.; Denton, W.; Arnold, A.; Raffalt, P.C.; Yentes, J.M. On the calculation of sample entropy using continuous and discrete human gaitdata. Entropy 2018, 20, 764. [Google Scholar] [CrossRef]
- Trybek, P.; Nowakowsuki, M.; Salowka, J.; Spiechowicz, J.; Machura, L. Sample entropy of sEMG signals at different stages of rectal cancer treatment. Entropy 2018, 20, 863. [Google Scholar] [CrossRef]
- Chou, C.M. Wavelet-based multi-scale entropy analysis of complex rainfall time series. Entropy 2011, 13, 241–253. [Google Scholar] [CrossRef]
- Hong, T.; Zhang, X.; Ma, H.J.; Chen, Y.; Chen, X. Fatiguing effects on the multi-scale entropy of surface electromyography in children with cerebral palsy. Entropy 2016, 18, 177. [Google Scholar] [CrossRef]
- Wu, T.Y.; Yu, C.L.; Liu, D.C. On Multi-scale entropy analysis of order-tracking measurement for bearing fault diagnosis under variable speed. Entropy 2016, 18, 292. [Google Scholar] [CrossRef]
- Pham, T.D. Time-shift multiscale entropy analysis of physiological signals. Entropy 2017, 19, 257. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inform. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Li, J.; Tang, J.T.; Xu, Z.M.; Yan, H. Magnetotelluric noise suppression base on signal-to-noise identification in ore concentration area. Chin. J. Geophys. 2017, 60, 722–737. [Google Scholar]
- Amaralsilva, H.; Wichertana, L.; Murta, L.O.; Romualdosuzuki, L.; Itikawa, W.; Bussato, G.F.; Azevedomarques, P. The superiority of tsallis entropy over traditional cost functions for brain MRI and SPECT registration. Entropy 2014, 16, 1632–1651. [Google Scholar] [CrossRef]
- Li, G.; Xiao, X.; Tang, J.T.; Li, J.; Zhu, H.J.; Zhou, C.; Yan, F.B. Near-source noise suppression of AMT by compressive sensing and mathematical morphology filtering. Appl. Geophys. 2017, 14, 581–589. [Google Scholar] [CrossRef]
- Weckmann, U.; Magunia, A.; Ritter, O. Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme. Geophys. J. Int. 2005, 161, 635–652. [Google Scholar] [CrossRef] [Green Version]









| Type of Interference | NCC | SNR |
|---|---|---|
| Square wave interference | 0.9775 | 13.5165 |
| Triangular wave interference | 0.9610 | 11.5246 |
| Pulse interference | 0.9852 | 15.3308 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Cai, J.; Peng, Y.; Zhang, X.; Zhou, C.; Li, G.; Tang, J. Magnetotelluric Signal-Noise Identification and Separation Based on ApEn-MSE and StOMP. Entropy 2019, 21, 197. https://doi.org/10.3390/e21020197
Li J, Cai J, Peng Y, Zhang X, Zhou C, Li G, Tang J. Magnetotelluric Signal-Noise Identification and Separation Based on ApEn-MSE and StOMP. Entropy. 2019; 21(2):197. https://doi.org/10.3390/e21020197
Chicago/Turabian StyleLi, Jin, Jin Cai, Yiqun Peng, Xian Zhang, Cong Zhou, Guang Li, and Jingtian Tang. 2019. "Magnetotelluric Signal-Noise Identification and Separation Based on ApEn-MSE and StOMP" Entropy 21, no. 2: 197. https://doi.org/10.3390/e21020197
APA StyleLi, J., Cai, J., Peng, Y., Zhang, X., Zhou, C., Li, G., & Tang, J. (2019). Magnetotelluric Signal-Noise Identification and Separation Based on ApEn-MSE and StOMP. Entropy, 21(2), 197. https://doi.org/10.3390/e21020197







