An Overview on Denial-of-Service Attacks in Control Systems: Attack Models and Security Analyses
Abstract
1. Introduction
2. An Overview of Literature on Denial-of-Service in Control Systems
2.1. Networked Control Problem
2.1.1. Discrete-Time Setting
2.1.2. Continuous-Time Setting
2.2. Networked State Estimation Problem
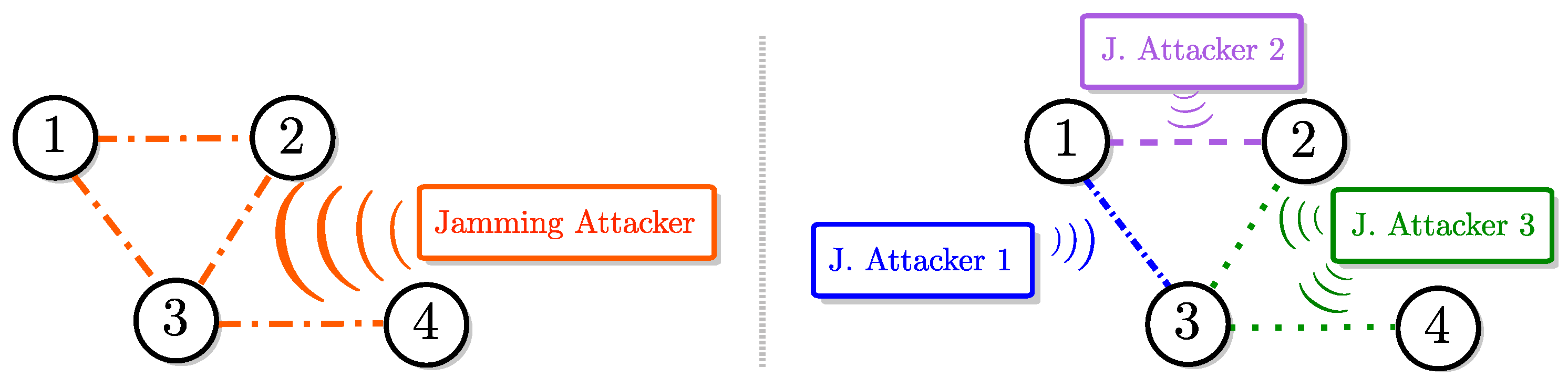
2.3. Multi-Agent Consensus Problem
3. Deterministic and Game-Theoretical Approaches to Denial-of-Service Attack Modeling
3.1. Deterministic Attack Models with Average Duration and Frequency Constraints
3.2. Game-Theoretic and Optimization-Based Approaches for Attack Modeling
3.2.1. Constraint-Based Models with Binary Actions
3.2.2. SINR-Based Models
4. Probabilistic Approaches to Models of DoS Attacks and Non-Malicious Transmission Failures
4.1. SINR-Based Probabilistic Jamming Models
4.2. Multi-Hop Network Models
5. An Overview of Attack-Resilient Control and Communication Techniques
5.1. Resilient Control Approaches
5.1.1. Event-Triggered Control
5.1.2. Control Frameworks with Predictors and Buffers
5.2. Resilient Communication Techniques
5.2.1. Self-Triggered and Randomized Communication Techniques in Multi-Agent Consensus
5.2.2. Fake Acknowledgement Messages in State Estimation
5.2.3. Design of Routing Protocols to Ensure Security Against DoS
6. Conclusions
Funding
Conflicts of Interest
References
- Cárdenas, A.A.; Amin, S.; Sastry, S. Research challenges for the security of control systems. In Proceedings of the 3rd Conference on Hot Topics in Security, San Jose, CA, USA, 28 July–1 August 2008. [Google Scholar]
- Sandberg, H.; Amin, S.; Johansson, K.H. Special issue on cyberphysical security in networked control systems. IEEE Control Syst. Mag. 2015, 35. [Google Scholar]
- Teixeira, A.; Shames, I.; Sandberg, H.; Johannson, K.H. A secure control framework for resource-limited adversaries. Automatica 2015, 51, 135–148. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H. A survey on security and privacy in emerging sensor networks: From viewpoint of close-loop. Sensors 2016, 16, 443. [Google Scholar] [CrossRef]
- Lun, Y.Z.; D’Innocenzo, A.; Smarra, F.; Malavolta, I.; Di Benedetto, M.D. State of the art of cyber-physical systems security: An automatic control perspective. J. Syst. Softw. 2019, 149, 174–216. [Google Scholar]
- Mo, Y.; Garone, W.; Casavola, A.; Sinopoli, B. False data injection attacks against state estimation in wireless sensor networks. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5967–5972. [Google Scholar]
- Teixeira, A.; Pérez, D.; Sandberg, H.; Johansson, K.H. Attack models and scenarios for networked control systems. In Proceedings of the 1st International Conference on High Confidence Networked Systems, Beijing, China, 17–18 April 2012; pp. 55–64. [Google Scholar]
- Fawzi, H.; Tabuada, P.; Diggavi, S. Secure estimation and control for cyber-physical systems under adversarial attacks. IEEE Trans. Autom. Control 2014, 59, 1454–1467. [Google Scholar] [CrossRef]
- Jhaveri, R.H.; Patel, S.J.; Jinwala, D.C. DoS attacks in mobile ad hoc networks: A survey. In Proceedings of the 2012 Second International Conference on Advanced Computing & Communication Technologies, Rohta, India, 7–8 January 2012; pp. 535–541. [Google Scholar]
- Mahmoud, M.M.E.A.; Shen, X.S. Security for Multi-hop Wireless Networks; Springer: New York, NY, USA, 2014. [Google Scholar]
- Marti, S.; Giuli, T.J.; Lai, K.; Baker, M. Mitigating routing misbehavior in mobile ad hoc networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 255–265. [Google Scholar]
- Awerbuch, B.; Holmer, D.; Nita-Rotaru, C.; Rubens, H. An on-demand secure routing protocol resilient to Byzantine failures. In Proceedings of the 1st ACM Workshop on Wireless Security, Atlanta, GA, USA, 28 September 2002; pp. 21–30. [Google Scholar]
- Just, M.; Kranakis, E.; Wan, T. Resisting malicious packet dropping in wireless ad hoc networks. In Proceedings of the International Conference on Ad-Hoc Networks and Wireless, Montreal, QC, Canada, 8–10 October 2003; pp. 151–163. [Google Scholar]
- Xu, W.; Ma, K.; Trappe, W.; Zhang, Y. Jamming sensor networks: Attack and defense strategies. IEEE Netw. 2006, 20, 41–47. [Google Scholar]
- Pelechrinis, K.; Iliofotou, M.; Krishnamurty, S.V. Denial of Service attacks in wireless networks: The case of jammers. IEEE Commun. Surv. Tut. 2011, 13, 245–257. [Google Scholar] [CrossRef]
- Fragkiadakis, A.; Askoxylakis, I.; Chatziadam, P. Denial-of-Service attacks in wireless networks using off-the-shelf hardware. In Proceedings of the nternational Conference on Distributed, Ambient, and Pervasive Interactions, Heraklion, Greece, 22–27 June 2014; pp. 427–438. [Google Scholar]
- Mizrak, A.T.; Savage, S.; Marzullo, K. Detecting malicious packet losses. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 191–206. [Google Scholar] [CrossRef]
- Shu, T.; Krunz, M. Privacy-preserving and truthful detection of packet dropping attacks in wireless ad hoc networks. IEEE Trans. Mob. Comput. 2015, 14, 813–828. [Google Scholar] [CrossRef]
- Wood, A.D.; Stankovic, J.A. Denial of service in sensor networks. Computer 2002, 35, 54–62. [Google Scholar] [CrossRef]
- Loukas, G.; Öke, G. Protection against denial of service attacks: A survey. Comput. J. 2010, 53, 1020–1037. [Google Scholar] [CrossRef]
- Mahjabin, T.; Xiao, Y.; Sun, G.; Jiang, W. A survey of distributed denial-of-service attack, prevention, and mitigation techniques. Int. J. Distrib. Sens. Netw. 2017, 13, 1–32. [Google Scholar] [CrossRef]
- Zargar, S.T.; Joshi, J.; Tipper, D. A survey of defense mechanisms against distributed Denial of Service (DDoS) flooding attacks. IEEE Commun. Surv. Tut. 2013, 15, 2046–2069. [Google Scholar] [CrossRef]
- Dong, Y.; Zhou, P. Jamming attacks against control systems: A survey. In Intelligent Computing, Networked Control, and Their Engineering Applications, Proceedings of the International Conference on Life System Modeling and Simulation (LSMS 2017) and International Conference on Intelligent Computing for Sustainable Energy and Environment (ICSEE 2017), Nanjing, China, 22–24 September 2017; Springer: Singapore, 2017; pp. 566–574. [Google Scholar]
- Peng, C.; Sun, H.; Yang, M.; Wang, Y.L. A survey on security communication and control for smart grids under malicious cyber attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. Networked control under candom and malicious packet losses. IEEE Trans. Autom. Control 2017, 62, 2434–2449. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. The effect of time-varying jamming interference on networked stabilization. SIAM J. Control Optim. 2018, 56, 2398–2435. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. A probabilistic characterization of random and malicious failures communication failures in multi-Hop networked control. SIAM J. Control Optim. 2018, 56, 2398–2435. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. Analysis of stochastic switched systems with application to networked control under jamming attacks. IEEE Trans. Autom. Control 2019. [Google Scholar] [CrossRef]
- Kellett, C.M.; Mareels, I.M.Y.; Nešic, D. Stability results for networked control systems subject to packet dropouts. IFAC Proc. Vol. 2005, 38, 73–78. [Google Scholar] [CrossRef]
- Hespanha, J.P.; Naghshtabrizi, P.; Xu, Y. A survey of recent results in networked control systems. Proc. IEEE 2007, 95, 138–172. [Google Scholar] [CrossRef]
- Gupta, V.; Martins, N.C.; Baras, J.S. Optimal output feedback control using two remote sensors over erasure channels. IEEE Trans. Autom. Control 2009, 54, 1463–1476. [Google Scholar] [CrossRef]
- Okano, K.; Ishii, H. Stabilization of uncertain systems with finite data rates and Markovian packet losses. IEEE Trans. Control Netw. Syst. 2014, 1, 298–307. [Google Scholar] [CrossRef]
- Schenato, L.; Sinopoli, B.; Franceschetti, M.; Poolla, K.; Sastry, S.S. Foundations of control and estimation over lossy networks. Proc. IEEE 2007, 95, 163–187. [Google Scholar] [CrossRef]
- Amin, S.; Cárdenas, A.A.; Sastry, S.S. Safe and secure networked control systems under denial-of-service attacks. In Proceedings of the 12th International Conference on Hybrid Systems: Computation and Control (HSCC), San Francisco, CA, USA, 13–15 April 2009; pp. 31–45. [Google Scholar]
- Lai, S.; Chen, B.; Li, T.; Yu, L. Packet-based state feedback control under DoS attacks in cyber-physical systems. IEEE Trans. Circuits Syst. II 2019. [Google Scholar] [CrossRef]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. State-dependent jamming interference in networked stabilization. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 7249–7254. [Google Scholar]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. Wireless networked control facing combined effects of disturbance and jamming interference. In Proceedings of the 23rd International Symposium on Mathematical Theory of Networks and SystemsHong Kong University of Science and Technology, Hong Kong, China, 16–20 July 2018; pp. 387–392. [Google Scholar]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. Event-Triggered output feedback control resilient against jamming attacks and random packet losses. IFAC-PapersOnLine 2015, 22, 270–275. [Google Scholar] [CrossRef]
- Wakaiki, M.; Cetinkaya, A.; Ishii, H. Quantized output feedback stabilization under DoS attacks. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 6487–6492. [Google Scholar]
- Liu, S.; Li, S.; Xu, B. Event-triggered resilient control for cyber-physical system under denial-of-service attacks. Int. J. Control 2018, 1–13. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, P.; Shi, L.; Chen, J. Optimal denial-of-service attack scheduling against linear quadratic Gaussian control. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3996–4001. [Google Scholar]
- Befekadu, G.K.; Gupta, V.; Antsaklis, P.J. Risk-sensitive control under Markov modulated Denial-of-Service (DoS) attack strategies. IEEE Trans. Autom. Control 2015, 60, 3299–3304. [Google Scholar] [CrossRef]
- Li, H.; Lai, L.; Qiu, R.C. A denial-of-service jamming game for remote state monitoring in smart grid. In Proceedings of the 45th Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 23–25 March 2011; pp. 1–6. [Google Scholar]
- Smarra, F.; Benedetto, M.D.D.; D’Innocenzo, A. A sub-optimal method for routing redundancy design over lossy networks. IFAC-PapersOnLine 2017, 50, 2604–2609. [Google Scholar] [CrossRef]
- D’Innocenzo, A.; Di Benedetto, M.D.; Serra, E. Fault tolerant control of multi-hop control networks. IEEE Trans. Autom. Control 2013, 58, 1377–1389. [Google Scholar] [CrossRef]
- D’Innocenzo, A.; Smarra, F.; Di Benedetto, M.D. Resilient stabilization of multi-hop control networks subject to malicious attacks. Automatica 2016, 71, 1–9. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Resilient control under Denial-of-Service. IFAC Proc. Vol. 2014, 47, 134–139. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Input-to-state stabilizing control under denial-of-service. IEEE Trans. Autom. Control 2015, 60, 2930–2944. [Google Scholar] [CrossRef]
- Shisheh Foroush, H.; Martínez, S. On triggering control of single-input linear systems under pulse-width modulated DoS signals. SIAM J. Control Optim. 2016, 54, 3084–3105. [Google Scholar] [CrossRef]
- Feng, S.; Tesi, P. Networked control systems under denial-of-service: Co-located vs. remote architectures. Syst. Control Lett. 2017, 108, 40–47. [Google Scholar] [CrossRef]
- Feng, S.; Tesi, P. Resilient control under denial-of-service: Robust design. Automatica 2017, 79, 42–51. [Google Scholar] [CrossRef]
- Lu, A.Y.; Yang, G.H. Input-to-state stabilizing control for cyber-physical systems with multiple transmission channels under denial of service. IEEE Trans. Autom. Control 2018, 63, 1813–1820. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Networked control of nonlinear systems under denial-of-service. Syst. Control Lett. 2016, 96, 124–131. [Google Scholar] [CrossRef]
- Dolk, V.S.; Tesi, P.; De Persis, C.; Heemels, W.P.M.H. Event-triggered control systems under denial-of-service attacks. IEEE Trans. Control Netw. Syst. 2017, 4, 93–105. [Google Scholar] [CrossRef]
- Kato, R.; Cetinkaya, A.; Ishii, H. Stabilization of nonlinear networked control systems under denial-of-service attacks: A linearization approach. Proc. Amer. Control Conf. 2019. (to appear). [Google Scholar]
- An, L.; Yang, G.H. Decentralized adaptive fuzzy secure control for nonlinear uncertain interconnected systems against intermittent DoS attacks. IEEE Trans. Cybern. 2018, 49, 827–838. [Google Scholar] [CrossRef]
- Feng, S.; Tesi, P.; De Persis, C. Towards stabilization of distributed systems under denial-of-service. In Proceedings of the IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5360–5365. [Google Scholar]
- Tomic, I.; Breza, M.J.; Jackson, G.; Bhatia, L.; McCann, J.A. Design and evaluation of jamming resilient cyber-physical systems. In Proceedings of the IEEE International Conference on Cyber, Physical and Social Computing (CPSCom), Halifax, NS, Canada, 30 July–3 August 2018. [Google Scholar]
- Weitenberg, E.; De Persis, C.; Monshizadeh, N. Exponential convergence under distributed averaging integral frequency control. Automatica 2018, 98, 103–113. [Google Scholar] [CrossRef]
- Peng, C.; Li, J.; Fei, M. Resilient event-triggering H∞ load frequency control for multi-area power systems with energy-limited DoS attacks. IEEE Trans. Power Syst. 2017, 32, 4110–4118. [Google Scholar] [CrossRef]
- Feng, S.; Cetinkaya, A.; Ishii, H.; Tesi, P.; De Persis, C. Data rates for stabilizing control under denial-of-service attacks. Proc. Amer. Control Conf. 2019, (to appear). arXiv:1809.04892. [Google Scholar]
- Li, Y.; Shi, L.; Cheng, P.; Chen, J.; Quevedo, D.E. Jamming attacks on remote state estimation in cyber-physical systems: A game-theoretic approach. IEEE Trans. Autom. Control 2015, 60, 2831–2836. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, P.; Shi, L.; Chen, J. Optimal denial-of-service attack scheduling with energy constraint. IEEE Trans. Autom. Control 2015, 60, 3023–3028. [Google Scholar] [CrossRef]
- Qin, J.; Li, M.; Shi, L.; Yu, X. Optimal denial-of-service attack scheduling with energy constraint over packet-dropping networks. IEEE Trans. Autom. Control 2018, 63, 1648–1663. [Google Scholar] [CrossRef]
- Ding, K.; Ren, X.; Shi, L. Deception-based sensor scheduling for remote estimation under DoS attacks. IFAC-PapersOnLine 2016, 49, 169–174. [Google Scholar] [CrossRef]
- Li, Y.; Quevedo, D.E.; Dey, S.; Shi, L. SINR-based DoS attack on remote state estimation: A game-theoretic approach. IEEE Trans. Control Netw. Syst. 2017, 4, 632–642. [Google Scholar] [CrossRef]
- Ding, K.; Li, Y.; Quevedo, D.E.; Dey, S.; Shi, L. A multi-channel transmission schedule for remote state estimation under DoS attacks. Automatica 2017, 78, 194–201. [Google Scholar] [CrossRef]
- Yang, C.; Yang, W.; Shi, H. DoS attack in centralised sensor network against state estimation. IET Control Theory Appl. 2018, 12, 1244–1253. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, D.; Johansson, K.H.; Shi, L. Optimal linear cyber-attack on remote state estimation. IEEE Trans. Control Netw. Syst. 2017, 4, 4–13. [Google Scholar] [CrossRef]
- Guan, Y.; Ge, X. Distributed attack detection and secure estimation of networked cyber-physical systems against false data injection attacks and jamming attacks. IEEE Trans. Signal Inf. Process Netw. 2018, 4, 48–59. [Google Scholar] [CrossRef]
- Senejohnny, D.; Tesi, P.; De Persis, C. Self-triggered coordination over a shared network under denial-of-service. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 3469–3474. [Google Scholar]
- Kikuchi, K.; Cetinkaya, A.; Hayakawa, T.; Ishii, H. Stochastic communication protocols for multi-agent consensus under jamming attacks. In Proceedings of the IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 1657–1662. [Google Scholar]
- Senejohnny, D.; Tesi, P.; De Persis, C. A jamming-resilient algorithm for self-triggered network coordination. IEEE Trans. Control Netw. Syst. 2017, 5, 981–990. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, G. Distributed secure average consensus for linear multi-agent systems under DoS attacks. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 March 2017; pp. 2261–2266. [Google Scholar]
- Nugraha, Y.; Cetinkaya, A.; Hayakawa, T.; Ishii, H.; Zhu, Q. Subgame perfect equilibrium analysis for jamming attacks on resilient graphs. Proc. Amer. Control Conf. 2019. (to appear). [Google Scholar]
- Alpcan, T.; Başar, T. Network Security: A Decision and Game-Theoretic Approach; Cambridge University Press: Cambrifge, UK, 2010. [Google Scholar]
- Gupta, A.; Nayyar, A.; Langbort, C.; Başar, T. A dynamic transmitter-jammer game with asymmetric information. In Proceedings of the IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 6477–6482. [Google Scholar]
- Bhattacharya, S.; Gupta, A.; Başar, T. Jamming in mobile networks: A game-theoretic approach. J. Num. Algeb. Control Optim. 2013, 3, 1–30. [Google Scholar]
- Zhu, Q.; Saad, W.; Han, Z.; Poor, H.V.; Başar, T. Eavesdropping and jamming in next-generation wireless networks: A game-theoretic approach. In Proceedings of the IEEE MILCOM 2011 Military Communications Conference, Baltimore, MD, USA, 7–10 November 2011; pp. 119–124. [Google Scholar]
- Zhang, H.; Qi, Y.; Wu, J.; Fu, L.; He, L. DoS attack energy management against remote state estimation. IEEE Trans. Control Netw. Syst. 2018, 5, 383–394. [Google Scholar] [CrossRef]
- Yang, H.; Shi, M.; Xia, Y.; Zhang, P. Security research on wireless networked control systems subject to jamming attacks. IEEE Trans. Cybern. 2018, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Liu, H. SINR-based multi-channel power schedule under DoS attacks: A Stackelberg game approach with incomplete information. Automatica 2019, 100, 274–280. [Google Scholar] [CrossRef]
- Chen, J.; Touati, C.; Zhu, Q. A dynamic game analysis and design of infrastructure network protection and recovery. ACM SIGMETRICS Perf. Eval. Rev. 2017, 45, 125–128. [Google Scholar] [CrossRef]
- Ishii, H. Limitations in remote stabilization over unreliable channels without acknowledgements. Automatica 2009, 45, 2278–2285. [Google Scholar] [CrossRef]
- Klenke, A. Probability Theory: A Comprehensive Course; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Anantharamu, L.; Chlebus, B.S.; Kowalski, D.R.; Rokicki, M.A. Medium access control for adversarial channels with jamming. In Proceedings of the 18th International Colloquium SIROCCO, Gdańsk, Poland, 26–29 June 2011; pp. 89–100. [Google Scholar]
- Proano, A.; Lazos, L. Packet-hiding methods for preventing selective jamming attacks. IEEE Trans. Depend. Secure Comput. 2012, 9, 101–114. [Google Scholar] [CrossRef]
- Xiao, B.; Yu, B.; Gao, C. CHEMAS: Identify suspect nodes in selective forwarding attacks. J. Parallel Distr. Com. 2007, 67, 1218–1230. [Google Scholar] [CrossRef]
- Billingsley, P. Probability and Measure; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kallenberg, O. Foundations of Modern Probability; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- McDiarmid, C. Concentration. In Probabilistic Methods for Algorithmic Discrete Mathematics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 195–248. [Google Scholar]
- Fang, Y.; Loparo, K.; Feng, X. Stability of discrete time jump linear systems. J. Math. Syst. Estim. Control 1995, 5, 275–321. [Google Scholar]
- Bolzern, P.; Colaneri, P.; De Nicolao, G. On almost sure stability of discrete-time Markov jump linear systems. In Proceedings of the IEEE 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No.04CH37601), Nassau, Bahamas, 14–17 December 2004; pp. 3204–3208. [Google Scholar]
- Karlof, C.; Wagner, D. Secure routing in wireless sensor networks: Attacks and countermeasures. In Proceedings of the First IEEE International Workshop on Sensor Network Protocols and Applications, Anchorage, AK, USA, 11 May 2003; pp. 113–127. [Google Scholar]
- Singh, A.; Kalita, K.P.; Medhi, S.P. Blackhole attack on MANET and its effects. In Proceedings of the 5th International Conference on Computing for Sustainable Global Development, New Delhi, India, 14–16 March 2018; pp. 1–5. [Google Scholar]
- Sanzgiri, K.; Dahill, B.; Levine, B.N.; Shields, C.; Belding-Royer, E.M. A secure routing protocol for ad hoc networks. In Proceedings of the 10th IEEE International Conference on Network Protocols, Paris, France, 12–15 November 2002; pp. 78–87. [Google Scholar]
- Bianchi, A.; Pizzutilo, S.; Vessio, G. Intercepting blackhole attacks in MANETs: An ASM-based model. In Proceedings of the International Conference on Software Engineering and Formal Methods, Trento, Italy, 4–5 September 2017; pp. 137–152. [Google Scholar]
- Zhang, H.; Qi, Y.; Zhou, H.; Zhang, J.; Sun, J. Testing and defending methods against DoS attack in state estimation. Asian J. Control 2017, 19, 1295–1305. [Google Scholar] [CrossRef]
- Ali, Y.; Xia, Y.; Ma, L.; Hammad, A. Secure design for cloud control system against distributed denial of service attack. Control Theory Tech. 2018, 16, 14–24. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cetinkaya, A.; Ishii, H.; Hayakawa, T. An Overview on Denial-of-Service Attacks in Control Systems: Attack Models and Security Analyses. Entropy 2019, 21, 210. https://doi.org/10.3390/e21020210
Cetinkaya A, Ishii H, Hayakawa T. An Overview on Denial-of-Service Attacks in Control Systems: Attack Models and Security Analyses. Entropy. 2019; 21(2):210. https://doi.org/10.3390/e21020210
Chicago/Turabian StyleCetinkaya, Ahmet, Hideaki Ishii, and Tomohisa Hayakawa. 2019. "An Overview on Denial-of-Service Attacks in Control Systems: Attack Models and Security Analyses" Entropy 21, no. 2: 210. https://doi.org/10.3390/e21020210
APA StyleCetinkaya, A., Ishii, H., & Hayakawa, T. (2019). An Overview on Denial-of-Service Attacks in Control Systems: Attack Models and Security Analyses. Entropy, 21(2), 210. https://doi.org/10.3390/e21020210




