Bayesian Compressive Sensing of Sparse Signals with Unknown Clustering Patterns
Abstract
:1. Background and Introduction
1.1. Literature Review on SMV and MMVs
1.2. Idea Behind the Proposed Algorithm
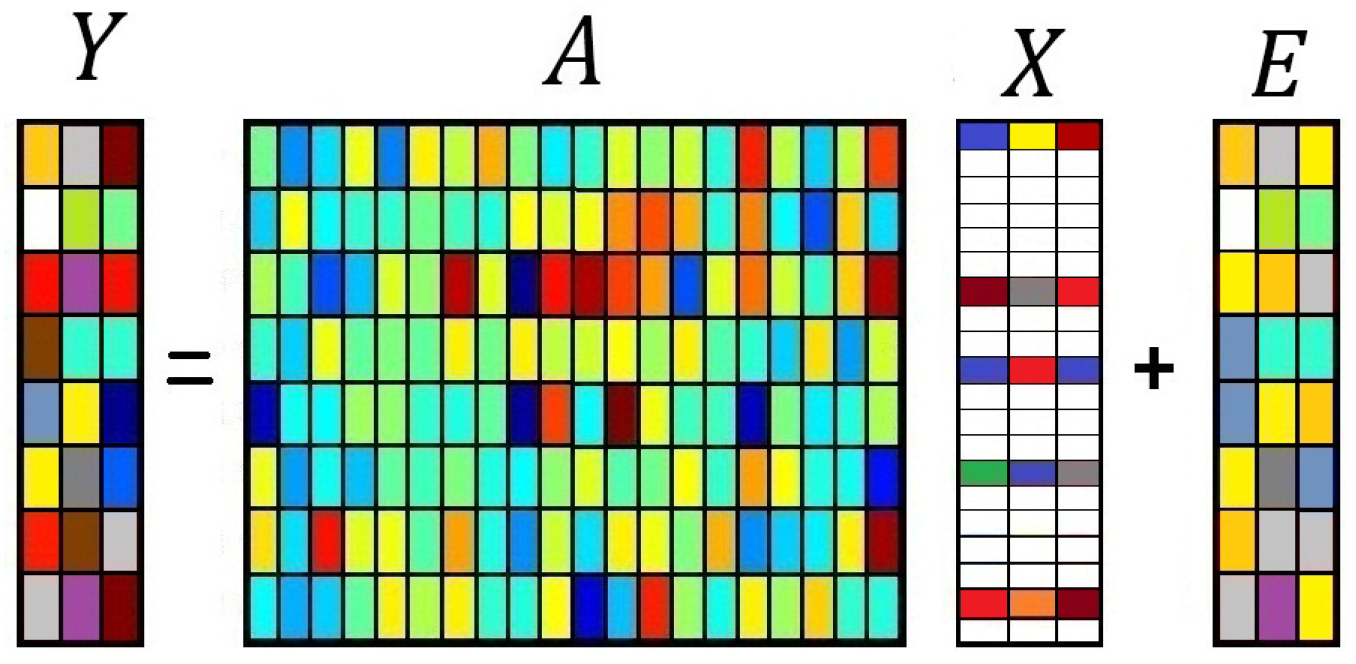
2. Initial Model: Sparse Bayesian Learning for MMVs
- where and .Here, , and the term is defined as:The Appendix provides more details.
- Therefore, .
- , where and .
- .Therefore, , where denotes the Frobenius norm. Finally,
- .Thus, .
| O-SBL Algorithm: |
| For |
| % Support-learning vector component |
| For |
| , |
| % Solution-value matrix component |
| For |
| End For{l} |
| End For{p} |
| , |
| End For{Iter} |
3. Clustered Sparse Bayesian Learning
- The posterior for is given by:where was defined in (7). Using the fact that is a binary random variable, the posterior inference on can be simplified to , where ,and:
- The posterior for is given by . Thus, where:
- The update rule for is determined as follows. Using the joint probability distribution of the complete model (12) and discarding the terms that are unrelated to , we have:Due to the complicated nature of (16), we estimate based on the current value of all the other variables and parameters of the model in the implemented MCMC approach. In other words, we compute:where is obtained by taking the logarithm of (16) and is defined as:and may be further simplified into:Taking the derivative of with respect to and equating the resulting equation to zero, we obtain:The maximum a posteriori point estimate of conditioned on the measurements and the current estimate of hidden variables and the parameters of the model can be obtained by iteratively solving:This update is computed at each iteration of the MCMC approach.
| C-SBL Algorithm: |
| For |
| % Support-learning vector component |
| For |
| , |
| , |
| % Solution-value matrix component |
| For |
| End For{l} |
| End For{p} |
| obtained from solving (20) for |
| , |
| End For{Iter} |
4. Simulation Results
4.1. Simulations on Synthetic Data
4.1.1. Performance for the SMV Problem
4.1.2. Performance for the MMV Problem with
4.1.3. Performance for the MMV Problem with
4.1.4. Interpretation of the results for the correlated case
4.2. Experiments on Real Data
Performance for the SMV Case (Experiments on MNIST Data)
4.3. Performance for the MMV Case (Experiments on Blind Multi-Narrowband Signal Sampling and Reconstruction
5. Convergence Diagnostics of the MCMC Implementation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Candes, E.J.; Romberg, J.; Tao, T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Li, K.; Gan, L.; Ling, C. Convolutional compressed sensing using deterministic sequences. IEEE Trans. Signal Process. 2013, 61, 740–752. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Elad, M. Sparse and Redundant Representation: From Theory to Applications in Signal and Image Processing; Springer: New York, NY, USA, 2010. [Google Scholar]
- Baraniuk, R.G. Compressive Sensing. IEEE Signal Process. Mag. 2007, 24, 118–124. [Google Scholar] [CrossRef]
- Mishali, M.; Eldar, Y.C. Reduce and Boost: Recovering Arbitrary Sets of Jointly Sparse Vectors. IEEE Trans. Signal Process. 2008, 56, 4692–4702. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Donoho, D. Basis Pursuit. In Proceedings of the 28th Asilomar Conference of Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–2 November 1994; pp. 41–44. [Google Scholar]
- Gill, P.R.; Wang, A.; Molnar, A. The in-Crowd Algorithm for Fast Basis Pursuit Denoising. IEEE Trans. Signal Process. 2011, 59, 4595–4605. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Becker, S.; Bobin, J.; Candes, E.J. NESTA: A Fast and Accurate First Order Method for Sparse Recovery. SIAM J. Imaging Sci. 2009, 4, 1–39. [Google Scholar] [CrossRef]
- Zhang, J.; Ghanem, B. ISTA-NET: Iterative Shrinkage-Thresholding Algorithm Inspired Deep Network for Image Compressive Sensing. arXiv, 2017; arXiv:1706.07929. [Google Scholar]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis pursuit Selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Rao, B.D. Recovery of Block Sparse Signals Using the Framework of Block Sparse Bayesian Learning. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3345–3348. [Google Scholar]
- Fang, J.; Shen, Y.; Li, F.; Li, H.; Chen, Z. Support Knowledge-Aided Sparse Bayesian Learning for Compressed Sensing. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 3786–3790. [Google Scholar]
- Cotter, S.F.; Rao, B.D.; Engan, K.; Delgado, K.K. Sparse Solutions to Linear Inverse Problem with Multiple Measurement Vectors. IEEE Trans. Signal Process. 2005, 53, 2477–2488. [Google Scholar] [CrossRef]
- Chen, J.; Huo, X. Theoretical Results on Sparse Representaions of Multiple-Measurement Vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar] [CrossRef]
- Ding, J.; Chen, L.; Gu, Y. Robustness of Orthogonal Matching Pursuit for Multiple Measurement Vectors in Noisy Scenario. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3813–3816. [Google Scholar]
- Hyder, M.M.; Mahata, K. A Robust Algorithm for Joint-Sparse Recovery. IEEE Signal Process. Lett. 2009, 16, 1091–1094. [Google Scholar] [CrossRef]
- Baron, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian Compressive Sensing via Belief Propagation. IEEE Trans. Signal Process. 2010, 58, 269–280. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An Empirical Bayesian Strategy for Solving the Simultaneous Sparse Approximation Problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Rao, B.D. Extension of SBL Algorithm for the Recovery of Block Sparse Signals With Intra-Block Correlation. IEEE Trans. Signal Process. 2013, 61, 2009–2015. [Google Scholar] [CrossRef]
- Mishali, M.; Eldar, Y.C. Xampling: Signal Acquisition and Processing in Union of Subspaces. IEEE Trans. Signal Process. 2011, 59, 4719–4734. [Google Scholar] [CrossRef] [Green Version]
- Kwon, H.; Rao, B.D. On the Benefits Of The block-Sparsity Structure In Sparse Signal Recovery. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3685–3688. [Google Scholar]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and Smoothness via the Fused Lasso. J. R. Stat. Soc. Ser. B 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Hernandez-Lobato, D.; Hernandez-Lobato, J.M.; Dupont, P. Generalized Spike-and-Slab Priors for Bayesian Group Feature Selection Using Expectation Propagation. J. Mach. Learn. Res. 2013, 14, 1891–1945. [Google Scholar]
- Fang, J.; Shen, Y.; Li, H.; Wang, P. Pattern-Coupled Sparse Bayesian Learning for Recovery of Block-Sparse Signals. IEEE Trans. Signal Process. 2015, 63, 360–372. [Google Scholar] [CrossRef]
- Luo, J.A.; Zhang, X.P.; Wang, Z. Direction-of-Arrival Estimation Using Sparse Variable Projection Optimization. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012; pp. 3106–3109. [Google Scholar]
- Eldar, Y.C.; Kuppinger, P.; Bolcskei, H. Block-Sparse Signals: Uncertainty Relations and Efficient Recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhang, T.; Metaxas, D. Learning with Structured Sparsity. J. Mach. Learn. Res. 2011, 12, 3371–3412. [Google Scholar]
- Yuan, M.; Lin, Y. Model Selection and Estimation in Regression with Grouped Variables. J. Mach. Learn. Soc. Ser. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, D.; Carin, L.; Dunson, D. Multi-Task Compressive Sensing with Dirichlet Process Priors. In Proceedings of the 25th international conference on Machine learning (ICML ’08), Helsinki, Finland, 5–9 July 2008; pp. 768–775. [Google Scholar]
- Ji, S.; Dunson, D.; Carin, L. Multitask Compressive Sensing. IEEE Trans. Signal Process. 2009, 57, 92–106. [Google Scholar] [CrossRef] [Green Version]
- Al-Shoukairi, M.; Rao, B.D. Sparse Bayesian Learning Using Approximate Message Passing. In Proceedings of the 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 1957–1961. [Google Scholar]
- Shekaramiz, M.; Moon, T.K.; Gunther, J.H. On the Block-Sparse Solution of Single Measurement Vectors. In Proceedings of the 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 508–512. [Google Scholar]
- Yu, L.; Sun, H.; Barbot, J.P.; Zheng, G. Bayesian Compressive Sensing for Cluster Structured Sparse Signals. Signal Process. 2012, 92, 259–269. [Google Scholar] [CrossRef]
- Anderson, M.R.; Winther, O.; Hansen, L.K. Bayesian Inference for Structured Spike and Slab Priors. Adv. Neural Inf. Process. Syst. 2014, 1745–1753. [Google Scholar]
- Meng, X.; Wu, S.; Kuang, L.; Huang, D.; Lu, J. AMP-NNSPL. arXiv, 2016; arXiv:1601.00543. [Google Scholar]
- Yu, L.; Wei, C.; Jia, J.; Sun, H. Compressive Sensing for Cluster Structured Sparse Signals: Variational Bayes Approach. IET Signal Process. 2016, 10, 770–779. [Google Scholar] [CrossRef]
- Ding, X.; He, L.; Carin, L. Bayesian Robust Principal Component Analysis. IEEE Trans. Image Proc. 2011, 20, 3419–3430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziniel, J.; Schniter, P. Efficient High-Dimensional Inference in the Multiple Measurement Vector Problem. IEEE Signal Process. Mag. 2013, 61, 340–354. [Google Scholar] [CrossRef] [Green Version]
- Cohen, D.; Mishra, K.V.; Eldar, Y.C. Spectrum Sharing Radar: Coexistence via Xampling. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1279–1296. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Zhang, L.; Li, H. Two-Dimensional Pattern-Coupled Sparse Bayesian Learning via Generalized Approximate Message Passing. IEEE Trans. Image Proc. 2016, 25, 2920–2930. [Google Scholar] [CrossRef] [PubMed]
- Vila, J.P.; Schniter, P. Expectation-Maximization Gaussian-Mixture Approximate Message Passing. IEEE Trans. Signal Proc. 2013, 61, 4658–4672. [Google Scholar] [CrossRef] [Green Version]
- Shekaramiz, M.; Moon, T.K.; Gunther, J.H. Hierarchical Bayesian Approach for Jointly-Sparse Solution of Multiple-Measurement Vectors. In Proceedings of the 48th Asilomar Conference of Signals, Systems, and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 1962–1966. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Grant, C.S.; Moon, T.K.; Gunther, J.H.; Stites, M.R.; Williams, G.P. Detection of Amorphously Shaped Objects Using Spatial Information Detection Enhancement (SIDE). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 478–487. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaifar, R.; Krishnaprasad, P.S. Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Friedlander, M.P.; Vanderberg, E. SPGL1 (version 1.9): A Solver for Large-Scale Sparse Reconstruction. Available online: https://www.cs.ubc.ca/~mpf/spgl1/ (accessed on 15 September 2018).
- Ji, S. MT-CS. Available online: http://people.ee.duke.edu/~lcarin/BCS.html (accessed on 21 August 2018).
- Fang, J.; Shen, Y. PC-SBL. Available online: http://junfang-uestc.net/swf/publication.html (accessed on 21 August 2018).
- Zhang, Z. Materials: Matlab-Codes. Available online: https://sites.google.com/site/researchbyzhang/software (accessed on 20 August 2018).
- Yu, L. Materials: Matlab-Codes. Available online: https://sites.google.com/site/link2yulei/publications/materials (accessed on 20 August 2018).
- Zhang, Z.; Rao, B.D. Sparse Signal Recovery with Temporally Correlated Source Vectors Using Sparse Bayesian Learning. IEEE J. Sel. Top. Signal Proc. 2011, 5, 912–926. [Google Scholar] [CrossRef]
- Zhang, Z.; Rao, B.D. Clarify Some Issues on the Sparse Bayesian Learning for Sparse Signal Recovery. Available online: http://dsp.ucsd.edu/~zhilin/papers/clarify.pdf (accessed on 20 September 2018).
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Documnet Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Bora, A.; Jalal, A.; Price, E.; Dimakis, A.G. Compressed Sensing Using Generative Models. arXiv, 2017; arXiv:1703.03208. [Google Scholar]
- Tramel, E.W.; Dremeau, A.; Krzakala, F. Approximate Message Passing with Restricted Boltzmann Machine Priors. J. Stat. Mech: Theory Exp. 2016, 2016, 073401. [Google Scholar] [CrossRef]
- Mousavi, H.S.; Monga, V.; Tran, T.D. Iterative Convex Refinement for Sparse Recovery. IEEE Signal Process. Lett. 2015, 22, 1903–1907. [Google Scholar] [CrossRef]
- Shekaramiz, M.; Moon, T.K.; Gunther, J.H. AMP-B-SBL: An Algorithm for Clustered Sparse Signals Using Approximate Message Passing. In Proceedings of the 2016 IEEE 7th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 20–22 October 2016; pp. 1–5. [Google Scholar]
- Palangi, H.; Ward, R.; Deng, L. Distributed Compressive Sensing: A Deep Learning Approach. IEEE Trans. Signal Process. 2016, 64, 4504–4518. [Google Scholar] [CrossRef]
- Chang, J.H.; Li, C.L.; Poczos, B.; Kumar, B.V.V.; Sankaranarayanan, A.C. One Network to Solve Them ALL- Solving Linear Inverse Problems Using Deep Projection Models. arXiv, 2017; arXiv:1703.09912. [Google Scholar]
- Vu, T.H.; Mousavi, H.S.; Monga, V. Adaptive Matching Pursuit for Sparse Signal Recovery. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 4331–4335. [Google Scholar]
- Mishali, M.; Eldar, Y.C. From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals. IEEE J. Sel. Top. Signal Process. 2010, 4, 375–391. [Google Scholar] [CrossRef] [Green Version]
- Mishali, M.; Eldar, Y.C. Blind Multiband Signal Reconstruction : Compressed Sensing for Analog Signals. IEEE Trans. Signal Process. 2009, 57, 993–1009. [Google Scholar] [CrossRef]
- Mishali, M.; Eldar, Y.C.; Tropp, J.A. Efficient Sampling of Sparse Wideband Sparse Analog Signals. In Proceedings of the 2008 IEEE 25th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 3–5 December 2008; pp. 290–294. [Google Scholar]
- Eldar, Y.C. MWC Matlab Package. Available online: http://webee.technion.ac.il/Sites/People/YoninaEldar/software_det2.php (accessed on 25 August 2018).
- Siguoyi. MWC matlab package. Available online: https://github.com/siguoyi/MWC/find/master (accessed on 25 August 2018).
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–511. [Google Scholar] [CrossRef]
- Brooks, S.P.; Gelman, A. General methods for Monitoring Convergence of Iterative Simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar]
- Kass, R.E.; Carlin, B.P.; Gelman, A.; Neal, R.M. Markov Chain Monte Carlo in Practice: A Roundtable Discussion. Am. Stat. Assoc. 1998, 52, 93–100. [Google Scholar]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference; University of London: London, UK, 2003. [Google Scholar]















| Algorithm | Digit 0 | Digit 1 | Digit 2 | Digit 3 | Digit 4 | Digit 5 | Digit 6 | Digit 7 | Digit 8 | Digit 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| C-SBL | 0.9530 | 0.9954 | 0.9592 | 0.9643 | 0.9834 | 0.9690 | 0.9847 | 0.9890 | 0.9250 | 0.9794 |
| BSBL [15,23,53] | 0.9204 | 0.9819 | 0.9341 | 0.8301 | 0.9617 | 0.9479 | 0.9116 | 0.9568 | 0.7469 | 0.9263 |
| PCSBL [28,52] | 0.7622 | 0.9544 | 0.8717 | 0.7281 | 0.8961 | 0.8270 | 0.8468 | 0.7787 | 0.5746 | 0.7046 |
| CLUSS [37,54] | 0.4265 | 0.6689 | 0.4803 | 0.4981 | 0.6421 | 0.5878 | 0.7179 | 0.6098 | 0.3123 | 0.4233 |
| MTCS [34,51] | 0.3030 | 0.4828 | 0.3380 | 0.4102 | 0.4779 | 0.4074 | 0.5989 | 0.5042 | 0.2740 | 0.3620 |
| MFOCUSS [17,53] | 0.3652 | 0.6510 | 0.4012 | 0.4378 | 0.5197 | 0.4961 | 0.5734 | 0.5054 | 0.2997 | 0.4324 |
| BPDN [50] | 0.3701 | 0.6360 | 0.4502 | 0.4161 | 0.5212 | 0.4967 | 0.5859 | 0.5370 | 0.3251 | 0.4052 |
| Algorithm | Digit 0 | Digit 1 | Digit 2 | Digit 3 | Digit 4 | Digit 5 | Digit 6 | Digit 7 | Digit 8 | Digit 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| True value | 208 | 80 | 290 | 306 | 166 | 316 | 220 | 240 | 358 | 168 |
| C-SBL | 244 | 78 | 266 | 284 | 176 | 324 | 196 | 241 | 340 | 172 |
| BSBL [15,23,53] | 320 | 84 | 402 | 458 | 200 | 344 | 262 | 276 | 750 | 228 |
| PCSBL [28,52] | 634 | 126 | 528 | 636 | 346 | 632 | 344 | 532 | 1080 | 560 |
| CLUSS [37,54] | 1018 | 370 | 960 | 758 | 570 | 804 | 446 | 664 | 1152 | 708 |
| MTCS [34,51] | 1774 | 1022 | 1742 | 1200 | 1194 | 1496 | 760 | 1178 | 1646 | 1298 |
| MFOCUSS [17,53] | 1532 | 878 | 1508 | 1082 | 936 | 1220 | 684 | 1124 | 1346 | 1186 |
| BPDN [50] | 1478 | 818 | 1440 | 1054 | 908 | 1192 | 646 | 1014 | 1352 | 1172 |
| Algorithm | Digit 0 | Digit 1 | Digit 2 | Digit 3 | Digit 4 | Digit 5 | Digit 6 | Digit 7 | Digit 8 | Digit 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| C-SBL | −8.0264 | −17.0256 | −9.2213 | −7.3822 | −13.9387 | −10.1113 | −13.9837 | −9.6984 | −3.7184 | −8.3104 |
| BSBL [15,23,53] | −11.6553 | −16.4167 | −12.0378 | −7.2124 | −13.5679 | −12.7994 | −11.3422 | −13.3647 | −5.4846 | −11.3947 |
| PCSBL [28,52] | −5.3168 | −13.1082 | −8.2997 | −4.9542 | −8.8138 | −6.8723 | −8.3111 | −5.3168 | −2.9960 | −4.1409 |
| CLUSS [37,54] | −1.5934 | −4.1480 | −2.1561 | −2.6419 | −4.1116 | −3.3908 | −6.1695 | −3.1560 | −0.9962 | −1.3608 |
| MTCS [34,51] | 0.4987 | −0.3990 | 0.1748 | −0.4367 | −0.9529 | −0.1357 | −2.6530 | −0.8175 | 0.6790 | 0.4506 |
| MFOCUSS [17,53] | −1.1638 | −3.1979 | −1.3832 | −1.7897 | −2.4664 | −2.2302 | −3.4462 | −2.2340 | −0.7605 | −1.4593 |
| BPDN [50] | −1.2096 | −3.0473 | −1.7805 | −1.6362 | −2.5115 | −2.2342 | −3.6447 | −2.5400 | −1.0469 | −1.3351 |
| Algorithm | OMP [5,49] | C-SBL | MTCS [34,51] | MFOCUSS [17,53] | MSBL [22,53] |
|---|---|---|---|---|---|
| NMSE (dB) | −17.5898 | −14.2124 | −3.3095 | −3.2028 | −1.7223 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shekaramiz, M.; Moon, T.K.; Gunther, J.H. Bayesian Compressive Sensing of Sparse Signals with Unknown Clustering Patterns. Entropy 2019, 21, 247. https://doi.org/10.3390/e21030247
Shekaramiz M, Moon TK, Gunther JH. Bayesian Compressive Sensing of Sparse Signals with Unknown Clustering Patterns. Entropy. 2019; 21(3):247. https://doi.org/10.3390/e21030247
Chicago/Turabian StyleShekaramiz, Mohammad, Todd K. Moon, and Jacob H. Gunther. 2019. "Bayesian Compressive Sensing of Sparse Signals with Unknown Clustering Patterns" Entropy 21, no. 3: 247. https://doi.org/10.3390/e21030247
APA StyleShekaramiz, M., Moon, T. K., & Gunther, J. H. (2019). Bayesian Compressive Sensing of Sparse Signals with Unknown Clustering Patterns. Entropy, 21(3), 247. https://doi.org/10.3390/e21030247







