A Study on the Hall–Petch Relationship and Grain Growth Kinetics in FCC-Structured High/Medium Entropy Alloys
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Grain Size Effect on Microhardness
3.2. Solid-Solution Effect on Microhardness
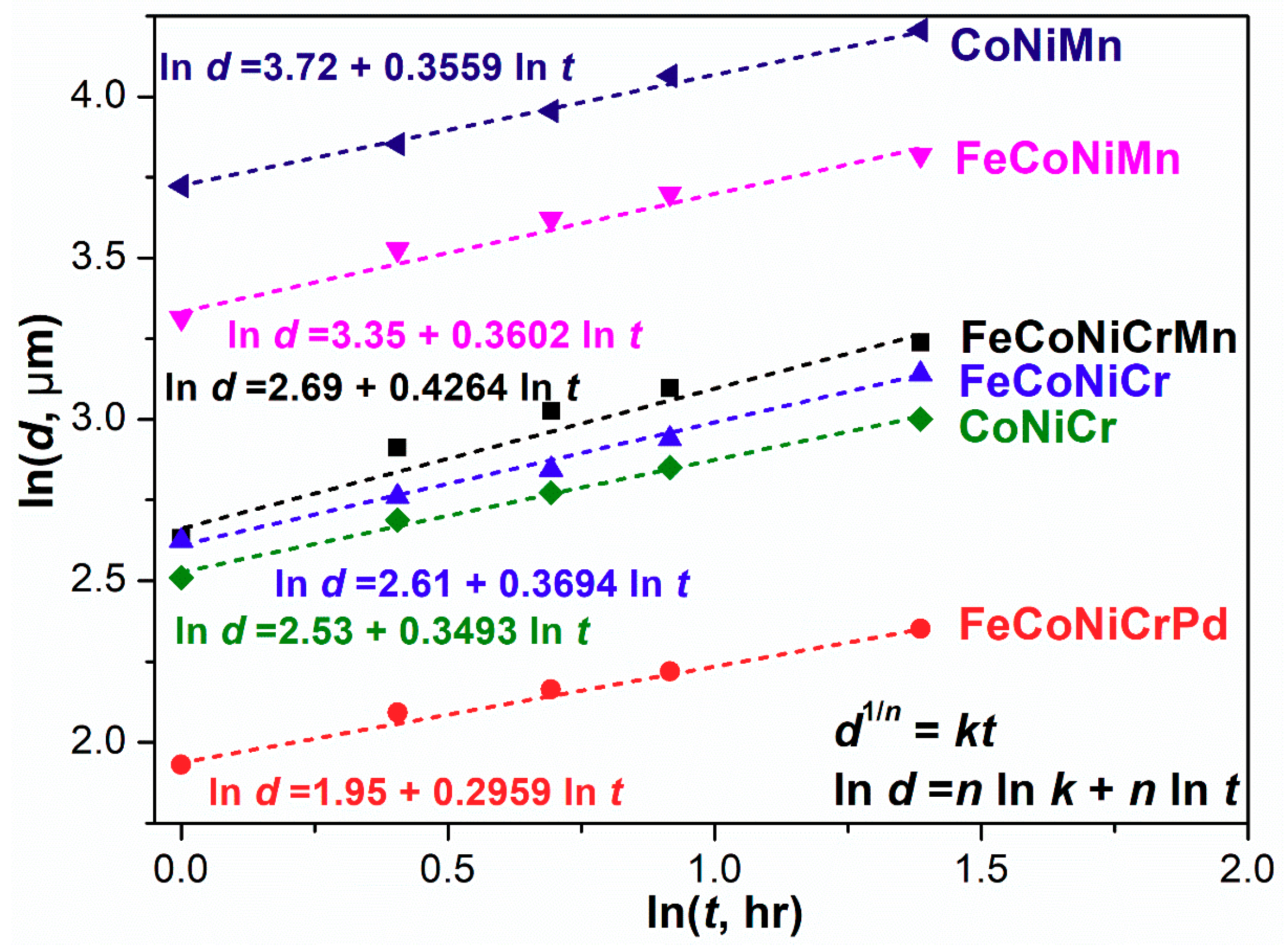
3.3. Grain Growth Kinetics Analysis
3.3.1. Grain Growth Exponent
3.3.2. Activation Energy QG for Grain Growth
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Miracle, D.B.; Miller, J.D.; Senkov, O.N.; Woodward, C.; Uchic, M.D.; Tiley, J. Exploration and development of high entropy alloys for structural applications. Entropy 2014, 16, 494–525. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef] [Green Version]
- Tsai, M.H.; Yeh, J.W. High-entropy alloys: A critical review. Mater. Res. Lett. 2014, 2, 107–123. [Google Scholar] [CrossRef]
- Yeh, J.W. Recent progress in high-entropy alloys. Ann. Chim.-Sci. Mater. 2006, 31, 633–648. [Google Scholar] [CrossRef]
- Yeh, J.W. Physical metallurgy of high-entropy alloys. JOM 2015, 67, 2254–2261. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Gali, A.; George, E.P. Tensile properties of high- and medium-entropy alloys. Intermetallics 2013, 39, 74–78. [Google Scholar] [CrossRef] [Green Version]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [Green Version]
- Laplanche, G.; Horst, O.; Otto, F.; Eggeler, G.; George, E.P. Microstructural evolution of a CoCrFeMnNi high-entropy alloy after swaging and annealing. J. Alloys Compd. 2015, 647, 548–557. [Google Scholar] [CrossRef]
- Liu, W.H.; Wu, Y.; He, J.Y.; Nieh, T.G.; Lu, Z.P. Grain growth and the Hall–Petch relationship in a high-entropy FeCrNiCoMn alloy. Scr. Mater. 2013, 68, 526–529. [Google Scholar] [CrossRef]
- Otto, F.; Dlouhy, A.; Somsen, C.; Bei, H.; Eggeler, G.; George, E.P. The influences of temperature and microstructure on the tensile properties of a CoCrFeMnNi high-entropy alloy. Acta Mater. 2013, 61, 5743–5755. [Google Scholar] [CrossRef] [Green Version]
- Otto, F.; Hanold, N.L.; George, E.P. Microstructural evolution after thermomechanical processing in an equiatomic, single-phase CoCrFeMnNi high-entropy alloy with special focus on twin boundaries. Intermetallics 2014, 54, 39–48. [Google Scholar] [CrossRef]
- Sathiaraj, G.D.; Bhattacharjee, P.P.; Tsai, C.W.; Yeh, J.W. Effect of heavy cryo-rolling on the evolution of microstructure and texture during annealing of equiatomic CoCrFeMnNi high entropy alloy. Intermetallics 2016, 69, 1–9. [Google Scholar] [CrossRef]
- Stepanov, N.; Tikhonovsky, M.; Yurchenko, N.; Zyabkin, D.; Klimova, M.; Zherebtsov, S.; Efimov, A.; Salishchev, G. Effect of cryo-deformation on structure and properties of CoCrFeNiMn high-entropy alloy. Intermetallics 2015, 59, 8–17. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Shaysultanov, D.G.; Yurchenko, N.Y.; Zherebtsov, S.V.; Ladygin, A.N.; Salishchev, G.A.; Tikhonovsky, M.A. High temperature deformation behavior and dynamic recrystallization in CoCrFeNiMn high entropy alloy. Mater. Sci. Eng. A 2015, 636, 188–195. [Google Scholar] [CrossRef]
- Wu, Z.; Bei, H.; Pharr, G.M.; George, E.P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
- He, J.Y.; Zhu, C.; Zhou, D.Q.; Liu, W.H.; Nieh, T.G.; Lu, Z.P. Steady state flow of the FeCoNiCrMn high entropy alloy at elevated temperatures. Intermetallics 2014, 55, 9–14. [Google Scholar] [CrossRef]
- Pickering, E.J.; Munoz-Moreno, R.; Stone, H.J.; Jones, N.G. Precipitation in the equiatomic high-entropy alloy CrMnFeCoNi. Scr. Mater. 2016, 113, 106–109. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Fu, L.M.; Liu, P.; Xu, X.D.; Chen, B.; Zhu, G.Z.; Wang, X.D.; Shan, A.D.; Chen, M.W. Deformation stimulated precipitation of a single-phase CoCrFeMnNi high entropy alloy. Intermetallics 2017, 85, 90–97. [Google Scholar] [CrossRef]
- Wu, Z.; Bei, H.; Otto, F.; Pharr, G.M.; George, E.P. Recovery, recrystallization, grain growth and phase stability of a family of FCC-structured multi-component equiatomic solid solution alloys. Intermetallics 2014, 46, 131–140. [Google Scholar] [CrossRef]
- Gwalani, B.; Soni, V.; Lee, M.; Mantri, S.A.; Ren, Y.; Banerjee, R. Optimizing the coupled effects of Hall–Petch and precipitation strengthening in a Al0.3CoCrFeNi high entropy alloy. Mater. Des. 2017, 121, 254–260. [Google Scholar] [CrossRef]
- Dąbrowa, J.; Zajusz, M.; Kucza, W.; Cieślak, G.; Berent, K.; Czeppe, T.; Kulik, T.; Danielewski, M. Demystifying the sluggish diffusion effect in high entropy alloys. J. Alloys Compd. 2019, 783, 193–207. [Google Scholar] [CrossRef]
- Jin, K.; Zhang, C.; Zhang, F.; Bei, H.B. Influence of compositional complexity on interdiffusion in ni-containing concentrated solid-solution alloys. Mater. Res. Lett. 2018, 6, 293–299. [Google Scholar] [CrossRef]
- Dahlborg, U.; Cornide, J.; Calvo-Dahlborg, M.; Hansen, T.C.; Fitch, A.; Leong, Z.; Chambreland, S.; Goodall, R. Structure of some CoCrFeNi and CoCrFeNiPd multicomponent HEA alloys by diffraction techniques. J. Alloys Compd. 2016, 681, 330–341. [Google Scholar] [CrossRef] [Green Version]
- ASTM Standard E112-12. Standard Test Methods for Determining Average Grain Size; ASTM International: West Conshohocken, PA, USA, 2014; pp. 1–27. [Google Scholar]
- Su, C.H. A Study on Hall–Petch Relationship and Grain Growth of Ternary to Quinary FCC-Structured Medium/High Entropy Alloys. Master’s Thesis, National Taiwan University, Taipei City, Taiwan, 2018; p. 52. [Google Scholar]
- Hall, E.O. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, J.Y.; Huang, J.C.; Bei, H.; Nieh, T.G. Grain-boundary strengthening in nanocrystalline chromium and the Hall–Petch coefficient of body-centered cubic metals. Scr. Mater. 2013, 68, 118–121. [Google Scholar] [CrossRef]
- Guo, S.; Hu, Q.; Ng, C.; Liu, C.T. More than entropy in high-entropy alloys: Forming solid solutions or amorphous phase. Intermetallics 2013, 41, 96–103. [Google Scholar] [CrossRef]
- Fischmeister, H.; Karlsson, B. Plasticity of 2-phase materials with a coarse microstructure. Z. Met. 1977, 68, 311–327. [Google Scholar]
- Wang, S.L.; Murr, L.E. Effect of prestrain and stacking-fault energy on the application of the Hall–Petch relation in FCC metals and alloys. Metallography 1980, 13, 203–224. [Google Scholar] [CrossRef]
- Gallagher, P.C.J. The influence of alloying, temperature, and related effects on the stacking fault energy. Metall. Trans. 1970, 1, 2429–2461. [Google Scholar]
- Kotval, P.S.; Nestor, O.H. The effects of solute additions on the stacking fault energy of a nickel-base superalloy. Trans. Metall. Soc. AIME 1969, 245, 1275–1278. [Google Scholar]
- Liu, S.F.; Wu, Y.; Wang, H.T.; He, J.Y.; Liu, J.B.; Chen, C.X.; Liu, X.J.; Wang, H.; Lu, Z.P. Stacking fault energy of face-centered-cubic high entropy alloys. Intermetallics 2018, 93, 269–273. [Google Scholar] [CrossRef]
- Shang, S.L.; Zacherl, C.L.; Fang, H.Z.; Wang, Y.; Du, Y.; Liu, Z.K. Effects of alloying element and temperature on the stacking fault energies of dilute Ni-base superalloys. J. Phys.-Condens. Matter 2012, 24, 505403. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Fujimoto, S.; Kambara, Y.; Kawamura, M.; Chen, Z.M.T.; Matsunoshita, H.; Tanaka, K.; Inui, H.; George, E.P. Size effect, critical resolved shear stress, stacking fault energy, and solid solution strengthening in the CrMnFeCoNi high-entropy alloy. Sci. Rep. 2016, 6, 35863. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhao, S.; Diao, H.; Liaw, P.K.; Meyers, M.A. High-velocity deformation of al0.3cocrfeni high-entropy alloy: Remarkable resistance to shear failure. Sci. Rep. 2017, 7, 42742. [Google Scholar] [CrossRef]
- Mishra, R.S.; Kumar, N.; Komarasamy, M. Lattice strain framework for plastic deformation in complex concentrated alloys including high entropy alloys. Mater. Sci. Technol. 2015, 31, 1259–1263. [Google Scholar] [CrossRef]
- Laplanche, G.; Kostka, A.; Reinhart, C.; Hunfeld, J.; Eggeler, G.; George, E.P. Reasons for the superior mechanical properties of medium-entropy CrCoNi compared to high-entropy CrMnFeCoNi. Acta Mater. 2017, 128, 292–303. [Google Scholar] [CrossRef]
- Kato, M. Hall-Petch relationship and dislocation model for deformation of ultrafine-grained and nanocrystalline metals. Mater. Trans. 2014, 55, 19–24. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Miracle, D.B.; Woodward, C.F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd. 2011, 509, 6043–6048. [Google Scholar] [CrossRef]
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Kaye, G.W.; Laby, T.H. Tables of Physical and Chemical Constants, 15th ed.; Longman: London, UK, 1993. [Google Scholar]
- James, A.M.; Lord, M.P. Macmillan’s Chemical and Physical Data; Macmillan: London, UK, 1992. [Google Scholar]
- Coury, F.G.; Clarke, K.D.; Kiminami, C.S.; Kaufman, M.J.; Clarke, A.J. High throughput discovery and design of strong multicomponent metallic solid solutions. Sci. Rep. 2018, 8, 8600. [Google Scholar] [CrossRef] [PubMed]
- Burke, J.E. Some factors affecting the rate of grain growth in metals. Trans. Am. Inst. Min. Metall. Eng. 1949, 180, 73–91. [Google Scholar]
- Beck, P.A.; Kremer, J.C.; Demer, L.J.; Holzworth, M.L. Grain growth in high-purity aluminum and in an aluminummagnesium alloy. Trans. Am. Inst. Min. Metall. Eng. 1948, 175, 372–400. [Google Scholar]
- Beck, P.A.; Towers, J.; Manly, W.D. Grain growth in 70-30 brass. Trans. Am. Inst. Min. Metall. Eng. 1948, 175, 162–177. [Google Scholar]
- Burke, J.E.; Turnbull, D. Recrystallization and grain growth. Prog. Met. Phys. 1952, 3, 220–292. [Google Scholar] [CrossRef]
- Drolet, J.P.; Galibois, A. The impurity-drag effect on grain growth. Acta Metall. Mater. 1968, 16, 1387–1399. [Google Scholar] [CrossRef]
- Fan, D.; Chen, S.P.; Chen, L.Q. Computer simulation of grain growth kinetics with solute drag. J. Mater. Res. 1999, 14, 1113–1123. [Google Scholar] [CrossRef] [Green Version]
- Hersent, E.; Marthinsen, K.; Nes, E. On the effect of atoms in solid solution on grain growth kinetics. Metall. Mater. Trans. A 2014, 45, 4882–4890. [Google Scholar] [CrossRef]
- Dillon, S.J.; Behera, S.K.; Harmer, M.P. An experimentally quantifiable solute drag factor. Acta Mater. 2008, 56, 1374–1379. [Google Scholar] [CrossRef]
- Gil, F.J.; Planell, J.A. Behaviour of normal grain growth kinetics in single phase titanium and titanium alloys. Mater. Sci. Eng. A 2000, 283, 17–24. [Google Scholar] [CrossRef]
- Singh, R.; Das, G.; Singh, P.K.; Chattoraj, I. Low-temperature sensitization behavior of base, heat-affected zone, and weld pool in AISI 304LN. Metall. Mater. Trans. A 2009, 40, 1219–1234. [Google Scholar] [CrossRef]
- Wang, X.; Hu, L.; Liu, K.; Zhang, Y. Grain growth kinetics of bulk AZ31 magnesium alloy by hot pressing. J. Alloys Compd. 2012, 527, 193–196. [Google Scholar] [CrossRef]
- Kucza, W.; Dabrowa, J.; Cieslak, G.; Berent, K.; Kulik, T.; Danielewski, M. Studies of “sluggish diffusion” effect in Co-Cr-Fe-Mn-Ni, Co-Cr-Fe-Ni and Co-Fe-Mn-Ni high entropy alloys; determination of tracer diffusivities by combinatorial approach. J. Alloys Compd. 2018, 731, 920–928. [Google Scholar] [CrossRef]
- Tsai, K.Y.; Tsai, M.H.; Yeh, J.W. Sluggish diffusion in Co-Cr-Fe-Mn-Ni high-entropy alloys. Acta Mater. 2013, 61, 4887–4897. [Google Scholar] [CrossRef]
- Higgins, G.T. Grain-boundary migration and grain growth. Met. Sci. 1974, 8, 143–150. [Google Scholar] [CrossRef]
- Gill, E.K.; Morrison, J.A. Kinetics of solids. Annu. Rev. Phys. Chem. 1963, 14, 205. [Google Scholar] [CrossRef]
- Cao, P.; Lu, L.; Lai, M.O. Grain growth and kinetics for nanocrystalline magnesium alloy produced by mechanical alloying. Mater. Res. Bull. 2001, 36, 981–988. [Google Scholar] [CrossRef]




| Alloy | Annealing Temperature T (°C) for 1 h | Grain Size d (μm) | Hardness H (Hv) | Alloy | Annealing Temperature T (°C) for 1 h | Grain Size d (μm) | Hardness H (Hv) |
|---|---|---|---|---|---|---|---|
| FeCoNiCrMn | 800 | 3.7 ± 0.9 | 176.6 ± 2.6 | FeCoNiMn | 800 | 9.8 ± 2.3 | 144.5 ± 1.2 |
| 900 | 13.9 ± 3.6 | 147.9 ± 2.2 | 900 | 27.5 ± 3.1 | 134.4 ± 1.9 | ||
| 1000 | 63.3 ± 9.6 | 136.1 ± 4.2 | 950 | 55.9 ± 10.5 | 127.6 ± 1.8 | ||
| 1100 | 120.2 ± 22.0 | 132.8 ± 2.8 | 1000 | 87.0 ± 8.4 | 121.9 ± 2.4 | ||
| 1200 | 209.6 ± 41.2 | 128.7 ± 2.4 | 1100 | 208.3 ± 27.2 | 118.9 ± 2.0 | ||
| FeCoNiCrPd | 900 | 6.9 ± 1.0 | 225.5 ± 0.9 | CoNiCr | 800 | 4.0 ± 0.5 | 255.1 ± 4.3 |
| 950 | 29.2 ± 5.2 | 208.4 ± 3.4 | 900 | 12.3 ± 3.3 | 195.5 ± 3.3 | ||
| 1000 | 47.1 ± 9.4 | 205.6 ± 2.1 | 1000 | 69.3 ± 6.0 | 158.0 ± 4.9 | ||
| 1100 | 108.9 ± 12.8 | 201.6 ± 1.0 | 1100 | 101.7 ± 17.4 | 153.3 ± 3.0 | ||
| 1200 | 292.7 ± 31.3 | 197.7 ± 3.5 | 1200 | 152.6 ± 19.2 | 151.5 ± 5.0 | ||
| FeCoNiCr | 800 | 4.2 ± 0.8 | 185.6 ± 4.0 | CoNiMn | 800 | 17.2 ± 2.4 | 157.8 ± 2.6 |
| 900 | 13.1 ± 3.3 | 154.9 ± 3.3 | 850 | 23.8 ± 2.6 | 150.9 ± 1.9 | ||
| 1000 | 64.2 ± 8.6 | 133.6 ± 2.5 | 900 | 41.4 ± 7.3 | 145.1 ± 1.5 | ||
| 1100 | 108.1 ± 14.8 | 129.1 ± 7.1 | 950 | 83.9 ± 13.7 | 139.8 ± 2.1 | ||
| 1200 | 153.9 ± 16.8 | 125.4 ± 3.7 | 1000 | 166.4 ± 18.6 | 136.5 ± 1.6 |
| Alloy | H0 (Hv) | KH (Hv·μm0.5) | δ × 100 | Shear Modulus (GPa) [18] |
|---|---|---|---|---|
| FeCoNiCrMn | 122.3 | 103.1 | 1.12 | 80 |
| FeCoNiCrPd | 193.0 | 85.2 | 3.66 | - |
| FeCoNiCr | 114.7 | 145.5 | 1.18 | 84 |
| FeCoNiMn | 112.4 | 104.1 | 0.89 | 77 |
| CoNiCr | 128.7 | 248.7 | 1.35 | 87 |
| CoNiMn | 126.0 | 126.8 | 0.99 | 77 |
| FeCoNiCrAl0.3 [23] | 111 | 227 | 3.64 | - |
| FeCoNiCrMn [12] | 125 | 69 | 1.12 | - |
| Element | Effective Radius (pm) [47] | Metallic Radius (pm) [44] | Young’s Modulus (GPa) [45,46] |
|---|---|---|---|
| Fe | 126.81 | 126 | 211 |
| Co | 124.46 | 125 | 209 |
| Ni | 123.28 | 124 | 200 |
| Cr | 129.25 | 128 | 279 |
| Mn | 127.52 | 127 | 198 |
| Pd | - | 137 | 121 |
| Al | - | 143 | 70 |
| Alloy | n | k |
|---|---|---|
| FeCoNiCrMn | 0.4264 | 549.3 |
| FeCoNiCrPd | 0.2959 | 727.8 |
| FeCoNiCr | 0.3694 | 1170.9 |
| FeCoNiMn | 0.3602 | 10942.3 |
| CoNiCr | 0.3493 | 1398.4 |
| CoNiMn | 0.3559 | 34626.5 |
| Alloy | QG (kJ/mol) | D0 [25] (10−4 m2/s) | QD [25] (kJ/mol) | Tm [25] (K) | D (10−4 m2/s) | δ× 100 |
|---|---|---|---|---|---|---|
| FeCoNiCrMn | 420.9 | 9.5 | 308 | 1553 | 9.3 | 1.12 |
| FeCoNiCrPd | 831.9 | 0.5 | 258 | 1560 | 0.5 | 3.66 |
| FeCoNiCr | 434.3 | 4.9 | 309 | 1695 | 4.8 | 1.18 |
| FeCoNiMn | 332.5 | DMn > DCr ~ DFe > DNi ~ DCo [59,60] | >9.3 | 0.89 | ||
| CoNiCr | 478.8 | 3.5 | 330 | 1690 | 3.4 | 1.35 |
| CoNiMn | 325.1 | DMn > DCr ~ DFe > DNi ~ DCo [59,60] | >9.3 | 0.99 | ||
| 304LN stainless steel [57] | 150 | - | - | - | ||
| AZ31 Mg alloy [58] | 110 | - | - | - | ||
| α-Ti-0.2Pd Ti alloy [56] | 133 | - | - | - | ||
| β-Ti-0.2Pd Ti alloy [56] | 56 | - | - | - | ||
| FeCoNiCrMn [12] | 321.7 | - | - | - | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.-C.; Su, C.-H.; Wu, S.-K.; Lin, C. A Study on the Hall–Petch Relationship and Grain Growth Kinetics in FCC-Structured High/Medium Entropy Alloys. Entropy 2019, 21, 297. https://doi.org/10.3390/e21030297
Huang Y-C, Su C-H, Wu S-K, Lin C. A Study on the Hall–Petch Relationship and Grain Growth Kinetics in FCC-Structured High/Medium Entropy Alloys. Entropy. 2019; 21(3):297. https://doi.org/10.3390/e21030297
Chicago/Turabian StyleHuang, Yung-Chien, Che-Hsuan Su, Shyi-Kaan Wu, and Chieh Lin. 2019. "A Study on the Hall–Petch Relationship and Grain Growth Kinetics in FCC-Structured High/Medium Entropy Alloys" Entropy 21, no. 3: 297. https://doi.org/10.3390/e21030297
APA StyleHuang, Y.-C., Su, C.-H., Wu, S.-K., & Lin, C. (2019). A Study on the Hall–Petch Relationship and Grain Growth Kinetics in FCC-Structured High/Medium Entropy Alloys. Entropy, 21(3), 297. https://doi.org/10.3390/e21030297




