Numerical Investigation on the Thermal Performance of Nanofluid-Based Cooling System for Synchronous Generators
Abstract
:1. Introduction
2. Idea of Nanofluid-Based Cooling System and Mathematic Models
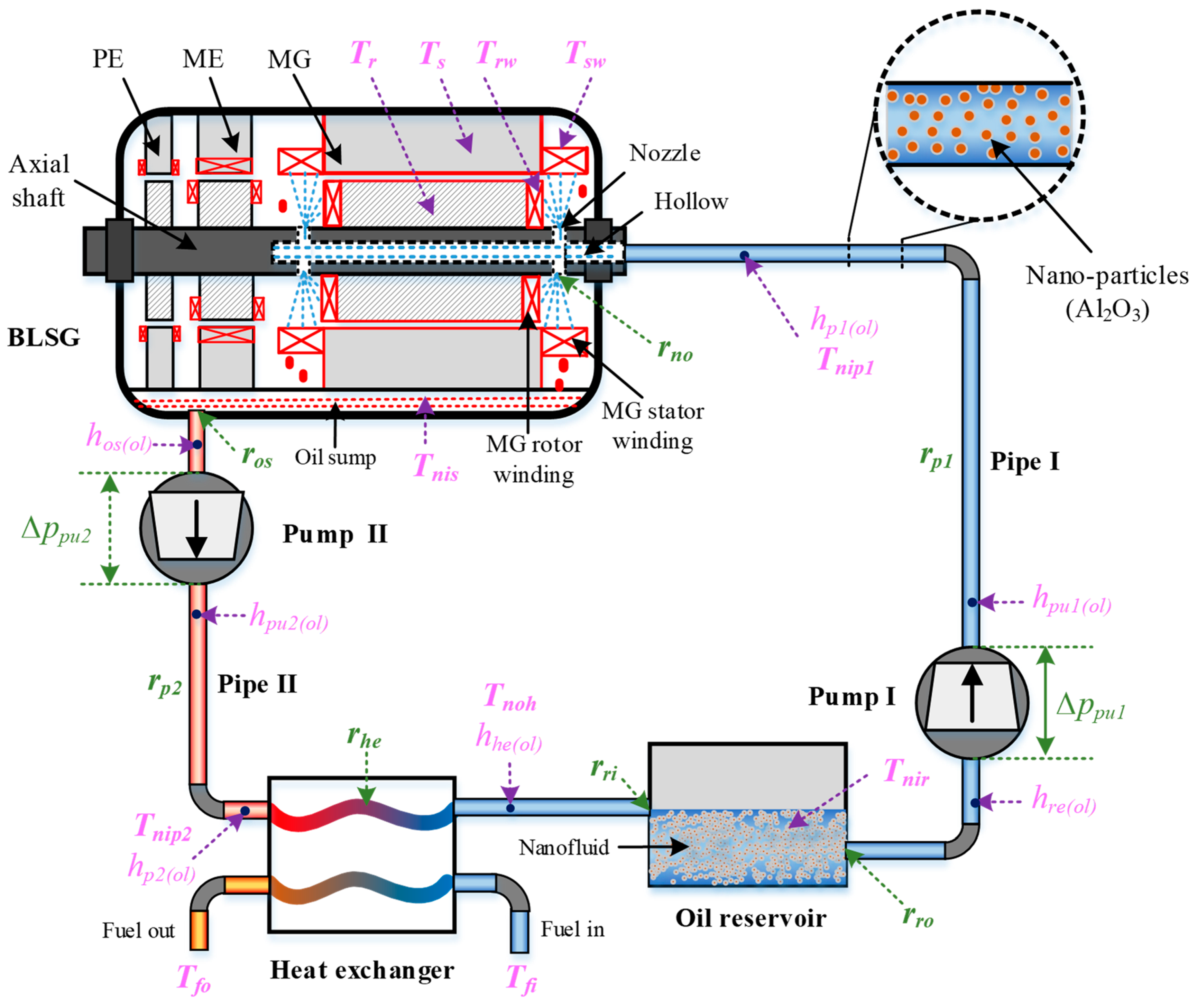
2.1. Idea of Nanofluid-Based Cooling System
2.1.1. Description of Nanofluid-Based Cooling System
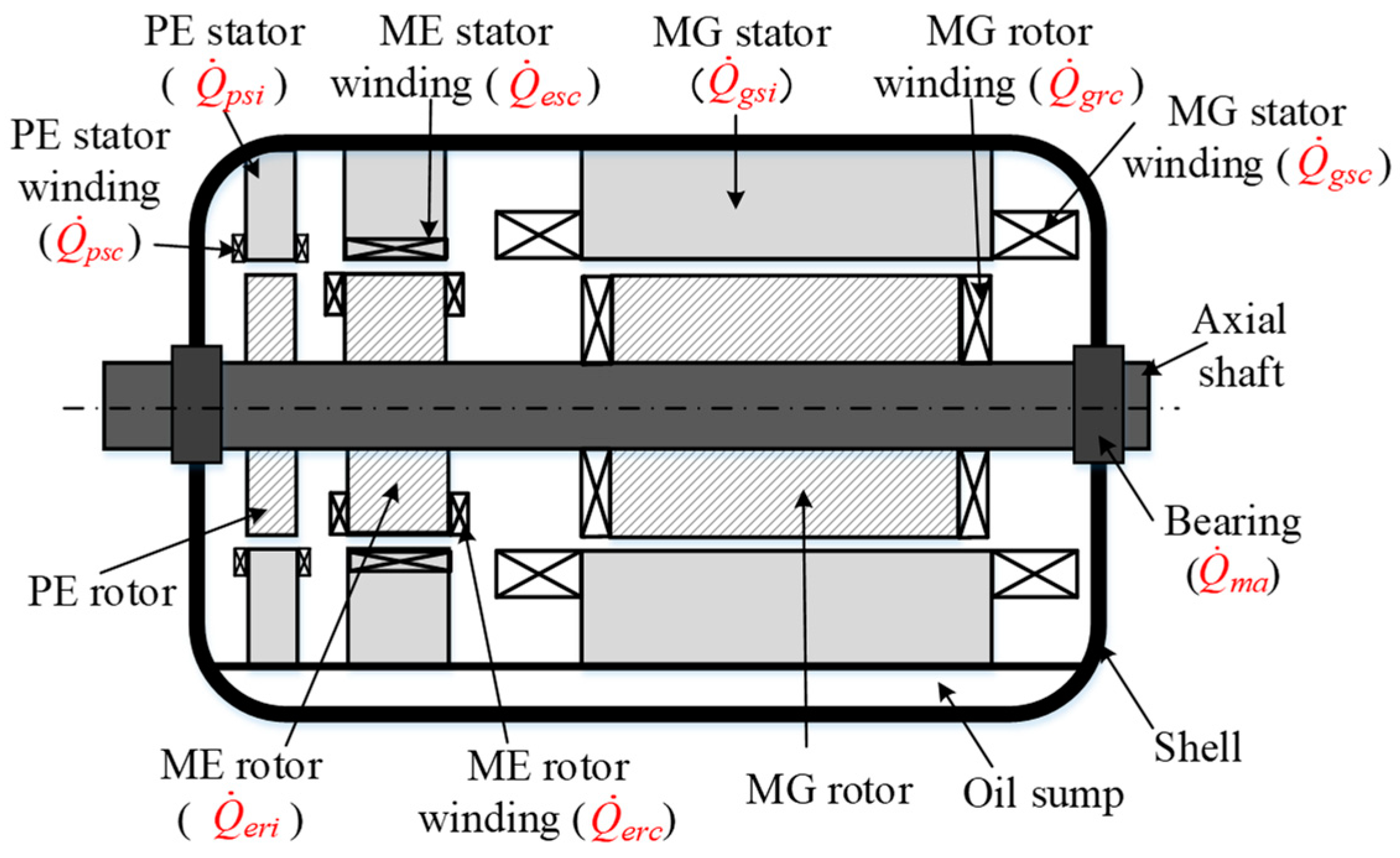
2.1.2. Cooling Object and Its Thermal Generation Performance
2.2. Mathematic Model of Nanofluid-Based Cooling Fluid
2.2.1. Models of Thermal State of Nanofluid-Based Cooling System
2.2.2. Models of Flow State of Nanofluid-Based Cooling System
2.2.3. Models of Key Parameters Impact on Thermal Transfer
2.3. The Calculation Processes
- (1)
- In the beginning, the calculation program is initialized where basic simulation parameters, including the NBCS physical parameters and initial work condition, are inputs. Additionally, the simulation step size and calculation time are set.
- (2)
- The NVF is set to calculate the nanofluid thermophysical properties using Equations (18)–(21).
- (3)
- According to the initial work condition, the convective heat transfer coefficients and can be obtained based on Equations (22)–(34).
- (4)
- In order to obtain the heat generation in Equation (2), the copper losses of the MG stator and rotor windings are calculated using Equation (3). After all power losses in BLSG are obtained, the efficiency of BLSG is calculated by using Equation (1).
- (5)
- All flow resistances in the NBCS and pump pressure heads and are calculated using Equations (10)–(14).
- (6)
- The pump input powers and can be calculated using Equations (15) and (16), respectively. Based on the power losses of BLSG and input power of the pumps obtained above, the efficiency of the NBCS is calculated by Equation (17).
- (7)
- The parameters obtained above are all submitted into the thermal state model of NBCS to conduct the thermal performance analysis based on Equations (2) and (4)–(9).
- (8)
- Lastly, some judgments need to be made. The first judgment is whether the thermal performance analysis is a steady-state analysis. If yes, it means that the simulation is used for steady-state thermal performance analysis. Then, the second judgment is whether the simulation reaches the steady-state. If the second judgment is no, the calculation will jump to step (4). If the second judgment is yes, the calculation step continues to the third judgment, which is whether the calculation will continue. If the third judgment is no, the simulation ends or it will jump to step (2). If the first judgment is no, the simulation is transient for thermal performance analysis. In the following, the fourth judgment, which is whether the calculation is finished need to be made, if yes, the simulation will jump to the third judgment, if not, the simulation jump to step (3).
3. Parameter Determinations and Simulation Cases
3.1. Physical Parameters and Initial Operation Condition
3.2. Simulation Cases Arrangement
3.2.1. Simulation Cases Arrangement for Steady-State Thermal Performance Analysis
3.2.2. Simulation Cases Arrangement for Transient Thermal Performance Analysis
3.2.3. Simulation Cases Arrangement for Power Loss and Efficiency Analysis
4. Results and Discussions
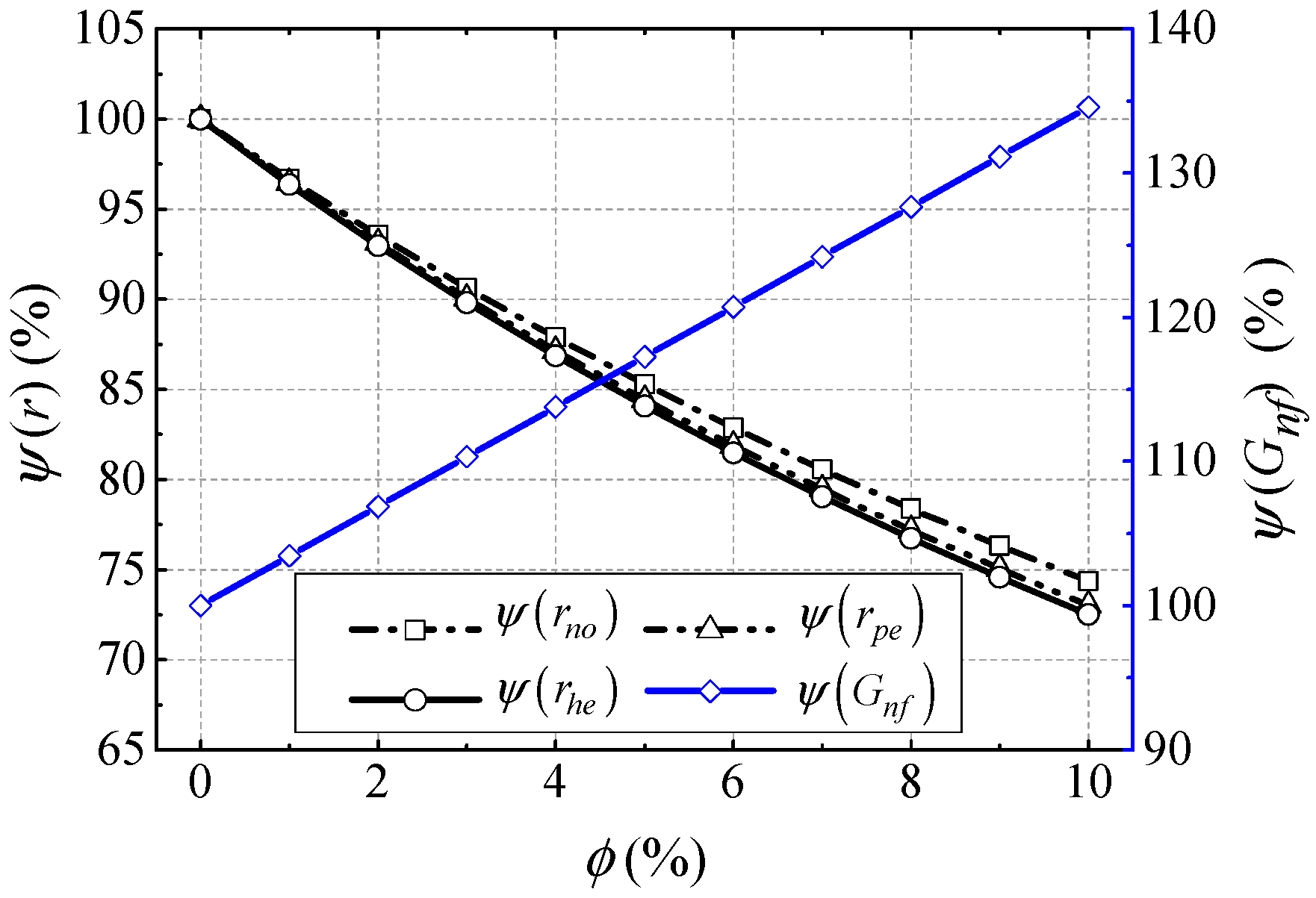
4.1. Effect of Thermal Properties of Nanofluid
4.2. Effect of Nanofluid on Steady-State Thermal Performance
4.3. Effect of Nanofluid on Transient Thermal Performance
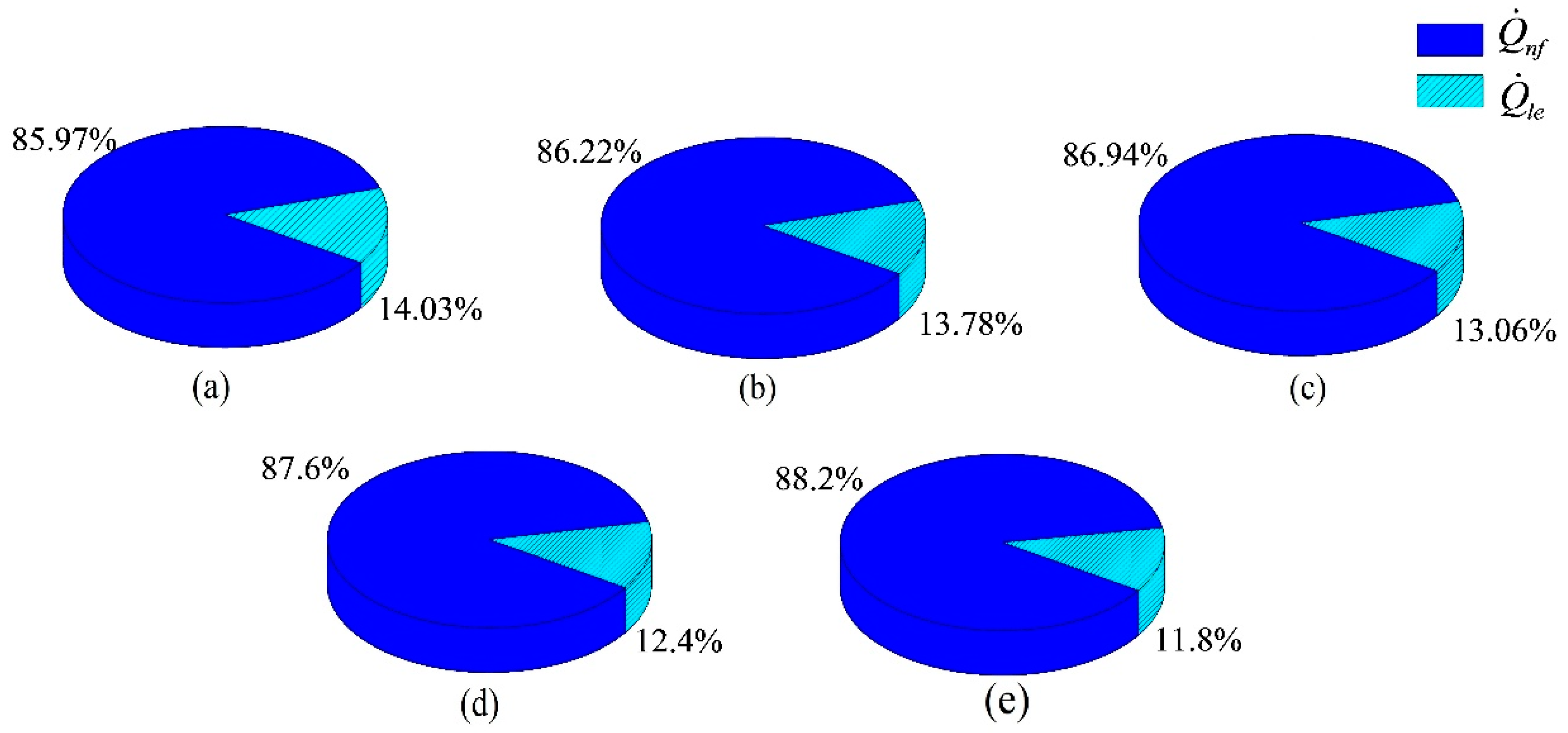
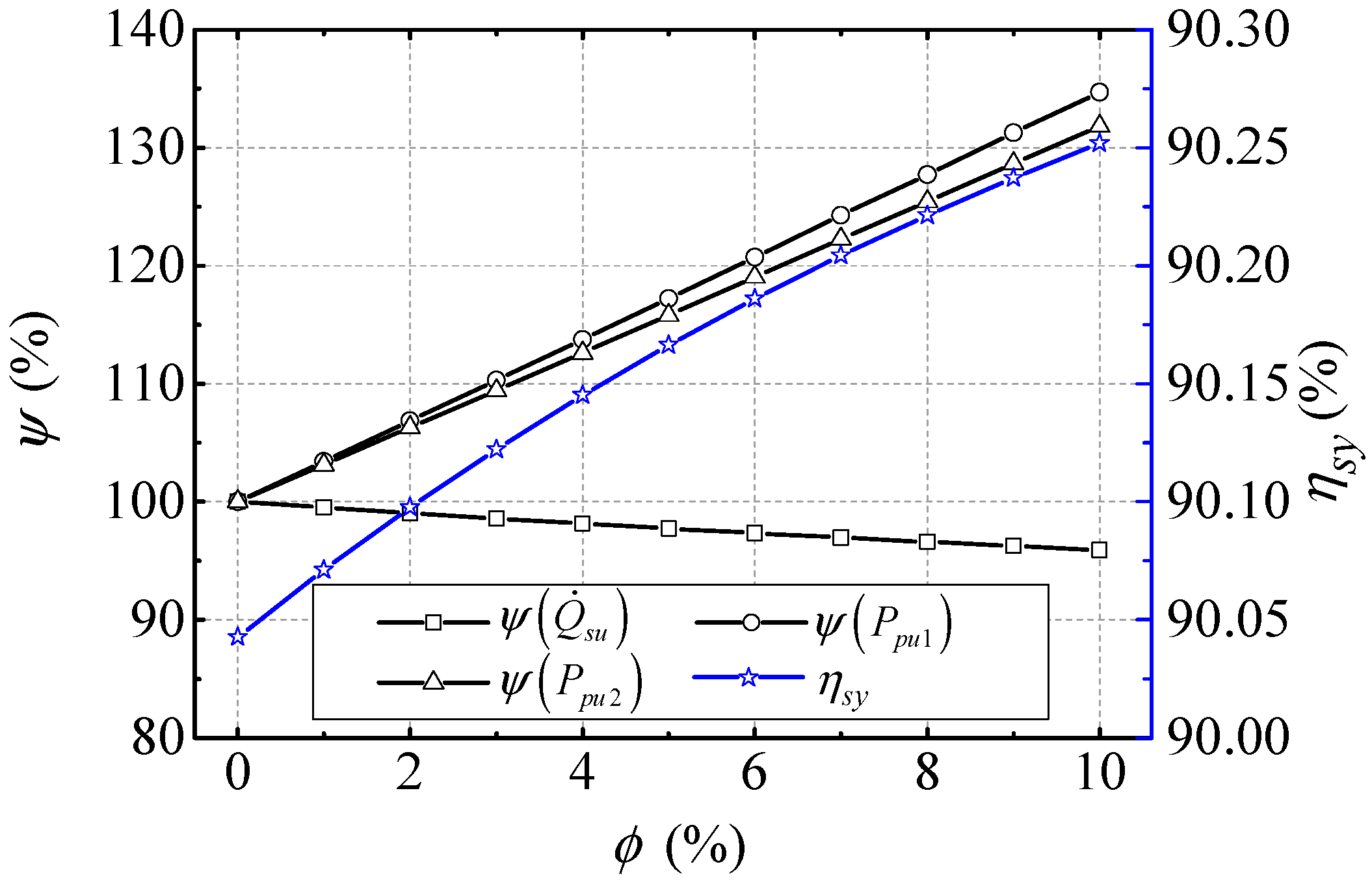
4.4. Effect of Nanofluid on BLSG System Power Losses and Efficiency
5. Conclusions
- (1)
- The heat transfer coefficient between the sprayed nanofluid and windings and that between the nanofluid and pipes are increased with the increase of nanoparticle volume fraction (NVF), their increments are 63% and 58%, respectively, when the NVF is 10%. The increasing heat transfer coefficients contribute to the heat dissipation of NBCS.
- (2)
- The steady-state thermal performance of NBCS is improved as the NVF increases. Specifically, when the NVF changes from 0% (base fluid) to 10%, the steady-state temperatures of MG stator and rotor winding are decreased by 33.2 °C and 36.9 °C, respectively, and the MG stator and rotor copper losses are decreased by 7.4% and 8.3%, respectively. The efficiency of BLSG is promoted by ~0.35%.
- (3)
- Since the settling time together with the dynamic changing ratios of the temperature of MG stator and rotor are decreased with the increase of NVF, the transient thermal performance of the NBCS is improved as the increase NVF.
- (4)
- As the NVF increased from 0% to 10%, the input power of the cycling pumps in the NBCS increased more than 30%, while the total power loss in BLSG has a ~4.1% decrease. However, since the power loss reduction in the BLSG is larger than the total increment of the input power of pumps, the efficiency of NBCD still has a slight promotion.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| sectional Area of duct (m2) | fuel out heat exchanger cold end | ||
| Nanofluid spray impact area (m2) | MG stator copper loss | ||
| specific heat (J/K) | MG stator iron loss | ||
| inner diameter (m) | MG rotor copper loss | ||
| Sauter mean diameter | BLSG | ||
| frequency (HZ) | heat exchanger hot end | ||
| bearing load (N) | Heat exchanger | ||
| mass flow rate (kg/s) | inlet | ||
| nanofluid entropy (J/kg) | Local fraction | ||
| armature current (A) | Leakage heat | ||
| friction flow resistance coefficient | machine loss | ||
| Local flow resistance coefficient | nanofluid | ||
| electrical resistance temperature coefficient | nozzle | ||
| length (m) | Total nozzles | ||
| mass (kg) | nanofluid in reservoir | ||
| Nusselt number | nanofluid in oil sump | ||
| pressure (Pa/m2) | nanofluid flow out of heat exchanger heat end | ||
| BLSG output power (W) | Lubrication oil | ||
| input power of pump I (W) | oil in sump | ||
| input power of pump II (W) | outlet | ||
| Peclet number | oil sump | ||
| Prandtl number, | oil in axle shaft | ||
| volumetric flow rate (L/s) | Nano-particles | ||
| power loss (W) | pipe I | ||
| flow resistance (Pa*s/m) | pipe II | ||
| thermal resistance (K/W) | PE stator copper loss | ||
| electrical resistance (Ω) | PE stator iron loss | ||
| Reynolds number | pump I | ||
| temperature (°C). | pump II | ||
| temperature gradient (°C/s) | MG rotor | ||
| volumetric flux (L/(m2*s)) | reservoir inlet | ||
| Greek symbols | reservoir outlet | ||
| convective heat transfer coefficient (W/(m2*°C/)) | MG rotor winding | ||
| thermal conductively (W/(m*k)) | Mg stator | ||
| angular velocity (rad/s) | spray | ||
| efficiency | BLSG shell | ||
| Density (kg/m3) | BLSG installation structure | ||
| viscosity (kg/(m*s)) | sum | ||
| phase number | MG stator winding | ||
| Nano-particle volume fraction | NBCS system | ||
| thermal diffusivity (m2/s) | total | ||
| subscript | winding | ||
| ambient | axle shaft | ||
| air in BLSDCG | |||
| Heat exchanger cold end | Between I and II, where I and II include , , , , , , , , , , , and | ||
| ME rotor copper loss | |||
| ME rotor iron loss | |||
| ME stator copper loss | The IV of III, III include , , , and , IV include il and ol. | ||
| fuel in heat exchanger cold end | |||
Appendix A

References
- Rosero, J.A.; Ortega, J.A.; Aldabas, E.; Romeral, L. Moving towards a more electric aircraft. IEEE Aerosp. Electron. Syst. Mag. 2007, 22, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.X.; Li, Y.Z.; Li, J.X.; Li, C.; Zhang, Y.; Ning, X.W. A gas-atomized spray cooling system integrated with an ejector loop: Ejector modeling and thermal performance analysis. Energy Convers. Manag. 2019, 180, 106–118. [Google Scholar] [CrossRef]
- Madonna, V.; Giangrande, P.; Galea, M. Electrical Power Generator in Aircraft: Review, Challenges, and Opportunities. IEEE Trans. Power Electrif. 2018, 4, 646–659. [Google Scholar]
- Zhang, X.; Bowman, C.L.; O’Connell, T.C.; Haran, K.S. Large electric machines for aircraft electric propulsion. IET Electr. Power Appl. 2018, 12, 767–779. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, W.; Zhao, D.; Mao, S.; Meng, T.; Jiao, N. Steady-state performance evaluations of three-phase brushless asynchronous excitation system for aircraft starter/generator. IET Electr. Power Appl. 2016, 10, 788–798. [Google Scholar] [CrossRef]
- Arumugam, D.; Logamani, P.; Karuppiah, S. Electromagnetic & Thermal analysis of synchronous generator with different rotor structures for aircraft application. Alex. Eng. J. 2018, 57, 1447–1457. [Google Scholar]
- Nakahama, T.; Suzuki, K.; Hashidume, S.; Ishibashi, F.; Hirata, M. Cooling Airflow in Unidirectional Ventilated Open-type Motor for Electric Vehicles. IEEE Trans. Energy Convers. 2006, 21, 645–651. [Google Scholar] [CrossRef]
- Grobler, A.J.; Holm, S.; Schoor, G.V. A Two-Dimensional Analytic Thermal Model for a High-Speed PMSM Magnet. IEEE Trans. Ind. Appl. 2015, 62, 6756–6764. [Google Scholar] [CrossRef]
- Kim, C.; Lee, K.S. Thermal nexus model for the thermal characteristic analysis of an open-type air-cooled induction motor. Appl. Therm. Eng. 2017, 112, 1108–1116. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Li, Y.Z.; Wang, J.; Xiao, X.; Guo, W. Transient cooling effect analysis for a permanent-magnet synchronous motor with phase-change material packing. Appl. Therm. Eng. 2016, 109, 251–260. [Google Scholar] [CrossRef]
- Wang, J.X.; Li, Y.Z.; Wang, S.N.; Zhang, H.S.; Ning, X.; Guo, W. Experimental investigation of the thermal control effects of phase change material based packaging strategy for on-board permanent magnet synchronous motors. Energy Convers. Manag. 2016, 23, 232–242. [Google Scholar] [CrossRef]
- Gharbi, S.; Harmand, S.; Jabrallah, S.B. Experimental comparison between different configurations of PCM based heat sinks for cooling electronic components. Appl. Therm. Eng. 2015, 87, 454–462. [Google Scholar] [CrossRef]
- Lim, D.H.; Kim, S.C. Thermal performance of oil spray cooling system for in-wheel motor in electric vehicles. Appl. Therm. Eng. 2014, 63, 577–587. [Google Scholar] [CrossRef]
- Wang, J.X.; Li, Y.Z.; Yu, X.K.; Li, G.C.; Ji, X.Y. Investigation of heat transfer mechanism of low environmental pressure large-space spray cooling for near-space flight systems. Int. J. Heat Mass Transf. 2018, 119, 496–507. [Google Scholar] [CrossRef]
- Davin, T.; Pelle, J.; Harmand, S.; Yu, R. Experimental study of oil cooling systems for electric motors. Appl. Therm. Eng. 2015, 75, 1–13. [Google Scholar] [CrossRef]
- Wang, J.X.; Li, Y.Z.; Li, G.C.; Ji, X.Y. Ground-based near-space-oriented spray cooling: Temperature uniformity analysis and performance prediction. Aiaa J. Thermophys. Heat Transf. 2019. [Google Scholar] [CrossRef]
- Sikora, M.; Vlach, R.; Navratil, P. The unusual water cooling applied on small asynchronous motor. Eng. Mech. 2011, 18, 143–153. [Google Scholar]
- Ravikumar, S.V.; Haldar, K.; Jha, J.M.; Chakraborty, S.; Sarkar, I.; Pal, S.K.; Chakraborty, S. Heat transfer enhancement using air-atomized spray cooling with water-Al2O3 nanofluid. Int. J. Therm. Sci. 2015, 96, 85–93. [Google Scholar] [CrossRef]
- Peyghambarzadeh, S.M.; Hashemabadi, S.H.; Hoseini, S.M.; Jamnani, M.S. Experimental study of heat transfer enhancement using water/ethylene glycol based nanofluids as a new coolant for car radiators. Int. Commun. Heat Mass. Transf. 2011, 38, 1283–1290. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K.; Namburu, P.K. Numerical study of fluid dynamic and heat transfer performance of Al2O3 and CuO nanofluids in the flat tubes of a radiator. Int. J. Heat Fluid Flow 2010, 31, 613–621. [Google Scholar] [CrossRef]
- Chinchole, A.S.; Dasgupta, A.; Kulkarni, P.P.; Chandraker, D.K.; Nayak, A.K. Exploring the use of alumina nanofluid as emergency coolant for nuclear fuel bundle. J. Therm. Sci. Eng. Appl. 2019, 11. [Google Scholar] [CrossRef]
- Ho, C.J.; Chiou, Y.H.; Yan, W.M.; Ghalambza, M. transient cooling characteristic of Al2O3-water nanofluid flow in the micro channel subject to sudden-pulsed heat flux. Int. J. Mech. Sci. 2019, 151, 95–105. [Google Scholar] [CrossRef]
- Kasaeian, A.; Eshghi, A.T.; Sameti, M. A review on the application on nanofluid on solar energy systems. Renew. Sustain. Energy Rev. 2015, 43, 584–598. [Google Scholar] [CrossRef]
- Pourfayaz, F.; Sanjarian, N.; Kasaeian, A.; Astaraei, F.R.; Sameti, M.; Nasirivatan, S. An experimental comparison of SiO2/water nanofluid heat transfer in square and circular cross-sectional channels. J. Therm. Anal. Calorim. 2018, 131, 1577–1586. [Google Scholar] [CrossRef]
- Sameti, M.; Haghighat, F. Hybrid solar and heat-driven district cooling system: Optimal integration and control strategy. Sol. Energy 2019, 183, 260–275. [Google Scholar] [CrossRef]
- Firouzfar, E.; Soltanieh, M.; Noie, S.H.; Saidi, S.H. Energy saving in HVAC systems using nanofluid. Appl. Therm. Eng. 2011, 31, 1543–1545. [Google Scholar] [CrossRef]
- Liu, W.; Feng, Y.; Yang, T.; Du, F.; Sun, J. Analysis of the induction heating efficiency and thermal energy conversion ability under different electromagnetic stick structures in the RPECT. Appl. Therm. Eng. 2018, 145, 277–286. [Google Scholar] [CrossRef]
- Hsieh, S.S.; Leu, H.Y.; Liu, H.H. Spray cooling characteristics of nanofluid for electronic power devices. Nano Scale Res. Lett. 2015, 10, 139. [Google Scholar] [CrossRef]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, T.V. Design of Rotating Electrical Machines; Wiley: Chichester, UK, 2013; pp. 457–463. [Google Scholar]
- Nan, X.; Sullivan, C.R. An improved calculation of proximity effect loss in high-frequency windings of round conductors. In Proceedings of the 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003; pp. 853–860. [Google Scholar]
- Murgatroyd, P.N. Calculation of proximity losses in multistranded conductor bunches. IEE Proc. Part A Phys. Sci. Meas. Instrum. Manag. Educ. 1989, 136, 115–120. [Google Scholar] [CrossRef]
- Bilgen, E.; Boulos, R. Functional dependence of torque coefficient of coaxial cylinders on gap width and Reynolds numbers. Trans. ASME J. Fluids Eng. 1973, 95, 122–126. [Google Scholar] [CrossRef]
- Xiong, K.; Li, Y.; Li, Y.Z.; Wang, J.X. Excitation current calculation of a brushless synchronous generator under different speed and load. In Proceedings of the 2018 15th ICARCV, Singapore, 18–21 November 2018; p. 733. [Google Scholar]
- Li, Y.Z.; Lee, K.M. Thermohydraulic dynamic and fuzzy coordination control of a microchannel cooling network for space electronics. IEEE Trans. Ind. Electron. 2011, 58, 700–708. [Google Scholar] [CrossRef]
- Guo, W.; Li, Y.; Li, Y.Z.; Zhong, M.L.; Wang, S.N.; Wang, J.X.; Li, E.H. An integrated hardware-in-loop verification approach for dual heat sink systems of aerospace single phase mechanically pumped fluid loop. Appl. Therm. Eng. 2016, 106, 1403–1414. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, C.; Liu, S.; Tang, Y.; Yin, Y. Effects of nanoparticle clustering and alignment on thermal conductivities of Fe3O4 aqueous nanofluid. Appl. Phys. Lett. 2006, 89, 023123. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 2nd ed.; Oxford University Press: Cambridge, UK, 1904. [Google Scholar]
- Drew, D.A.; Passman, S.L. Theory of Multicomponent Fluids; Springer: Berlin, Germany, 1999. [Google Scholar]
- Rybicki, J.R.; Mudawar, I. Single-phase and two-phase cooling characteristics of upward-facing and downward-facing sprays. Int. J. Heat Mass Trans. 2006, 49, 5–16. [Google Scholar] [CrossRef]
- Kim, J. Spray cooling heat transfer: The state of the art. Int. J. Heat Fluid Fl. 2007, 28, 753–767. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Investigation convective heat transfer and flow features of nanofluids. J. Heat Transf. 2002, 125, 151–155. [Google Scholar] [CrossRef]
- LMS imagine Lab. HYD advanced fluid properties, technical bulletin No. 117; BEL: LMS imagine Lab: Leuven, Belgium, 2007. [Google Scholar]
- Kaka, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Tran. 2009, 52, 3187–3196. [Google Scholar]
- Yu, W.; Choi, S.U.S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model. J. Nanoparticle Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. A Simplified Thermal Model for Variable Speed Self Cooled Industrial Induction Motor. IEEE Trans. Ind. Appl. 2003, 39, 945–952. [Google Scholar] [CrossRef]
- Hao, X.H.; Peng, B.; Chen, Y.; Xie, G.N. Transient thermal model of a permanent magnet synchronous planar motor considering spreading thermal resistance. Appl. Therm. Eng. 2015, 81, 1–9. [Google Scholar] [CrossRef]
- Roshen, W.A.; Practical, A. Accurate and Very General Core Loss Model for Nonsinusoidal Waveforms. IEEE Trans. Power Electron. 2007, 22, 30–40. [Google Scholar] [CrossRef]
- Nerg, J.; Rilla, M.; Pyrhonen, J. Thermal analysis of radial-flux electrical Machines with a high power density. IEEE Trans. Ind. Electron. 2008, 55, 3543–3554. [Google Scholar] [CrossRef]
- Xiong, K.; Li, Y.H.; Dong, S.J. Temperature distribution of a test specimen with high-speed heat airflow passing through. Therm. Sci. 2018, 22, 2527–2538. [Google Scholar] [CrossRef]
- Visaria, M.; Mudawar, I. Theoretical and experimental study of the effects of spray inclination on two-phase spray cooling and critical heat flux. Int. J. Heat Mass Transf. 2008, 51, 2398–2410. [Google Scholar] [CrossRef]






| Physical Parameter | Value | Initial Operating Condition | Value |
|---|---|---|---|
| voltage | 270 V | Rotate speed | 15000 r/min |
| Rated current | 240 A | Output power | 65 kW |
| Pole pairs | 6 | Coolant volume flow | 0.6143 L/s |
| BLSG Mass | 8.81 kg | Fuel inlet temperature | 65 °C |
| Winding temperature coefficient | 3.9 × 10−3 | Fuel mass flow | 0.8437 kg/s |
| Density (kg/m3) | Specific Heat (J/(kg*K)) | Thermal Conductively (W/(m*K)) | Viscosity (kg/(m*s)) | |
|---|---|---|---|---|
| Al2O3 particles | 3970 | 750 | 30 | - |
| Lubricating oil | 893 | 1909 | 0.14 | 0.028 |
| NVF | Operating Condition |
|---|---|
| 0%, 1%,2%, 3%, 4%, 5%, 6%, 7%,8%, 9%,10% | See in Table 1 |
| Case | Parameters | Initial Value | Final Value | Description | Particle Volume Fraction |
|---|---|---|---|---|---|
| Case I | BLSG output power | 65 (kW) | 52 (kW) | 20% step reduction | 0%, 1%, 4%, 7%,10% |
| Case II | Nanofluid volume flow rate | 0.6143 (L/s) | 0.4914 (L/s) | 20% step reduction | 0%, 1%, 4%, 7%,10% |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Stator copper loss | 1585.7 W | Pipe flow resistance | 1.163 × 106 Pa·s/m |
| Rotor copper loss | 1816.8 W | Pump I input power | 238.9 W |
| BLSG efficiency | 90.46% | Pump II input power | 93.8 W |
| BLSG system efficiency | 90.04% | Heat convection coefficient in pipe | 288.1 W/m2·K |
| MG stator winding temperature | 217.3 °C | Heat convection coefficient of spray | 817.6 W/m2·K |
| MG rotor winding temperature | 213.4 °C | Mass flow | 0.549 (kg/s) |
| reservoir oil temperature | 69.96 °C |
| NVF(%) | 0% | 1% | 4% | 7% | 10% |
|---|---|---|---|---|---|
| (W) | 5396.35 | 5383.2 | 5347.48 | 5316.39 | 5289.22 |
| (W) | 880.96 | 860.1 | 803.08 | 752.66 | 707.96 |
| (W) | 6277.31 | 6143.3 | 6150.56 | 6069.05 | 5997.18 |
| Cases | Temperature | 0% | 1% | 4% | 7% | 10% | |
|---|---|---|---|---|---|---|---|
| (s) | Case I | 140 | 136 | 126 | 117 | 109 | |
| 148 | 143 | 132 | 123 | 114 | |||
| Case II | 176 | 164 | 154 | 141 | 130 | ||
| 186 | 179 | 163 | 152 | 137 | |||
| (%) | Case I | −16.67 | −16.46 | −15.90 | −15.39 | −14.93 | |
| −15.32 | −15.08 | −14.43 | −13.83 | −13.29 | |||
| Case II | 14.25 | 14.09 | 13.57 | 13.17 | 12.78 | ||
| 16.60 | 16.41 | 15.75 | 15.27 | 14.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, K.; Li, Y.; Li, Y.-Z.; Wang, J.-X.; Mao, Y. Numerical Investigation on the Thermal Performance of Nanofluid-Based Cooling System for Synchronous Generators. Entropy 2019, 21, 420. https://doi.org/10.3390/e21040420
Xiong K, Li Y, Li Y-Z, Wang J-X, Mao Y. Numerical Investigation on the Thermal Performance of Nanofluid-Based Cooling System for Synchronous Generators. Entropy. 2019; 21(4):420. https://doi.org/10.3390/e21040420
Chicago/Turabian StyleXiong, Kai, Yunhua Li, Yun-Ze Li, Ji-Xiang Wang, and Yufeng Mao. 2019. "Numerical Investigation on the Thermal Performance of Nanofluid-Based Cooling System for Synchronous Generators" Entropy 21, no. 4: 420. https://doi.org/10.3390/e21040420
APA StyleXiong, K., Li, Y., Li, Y.-Z., Wang, J.-X., & Mao, Y. (2019). Numerical Investigation on the Thermal Performance of Nanofluid-Based Cooling System for Synchronous Generators. Entropy, 21(4), 420. https://doi.org/10.3390/e21040420






