Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux
Abstract
:1. Introduction
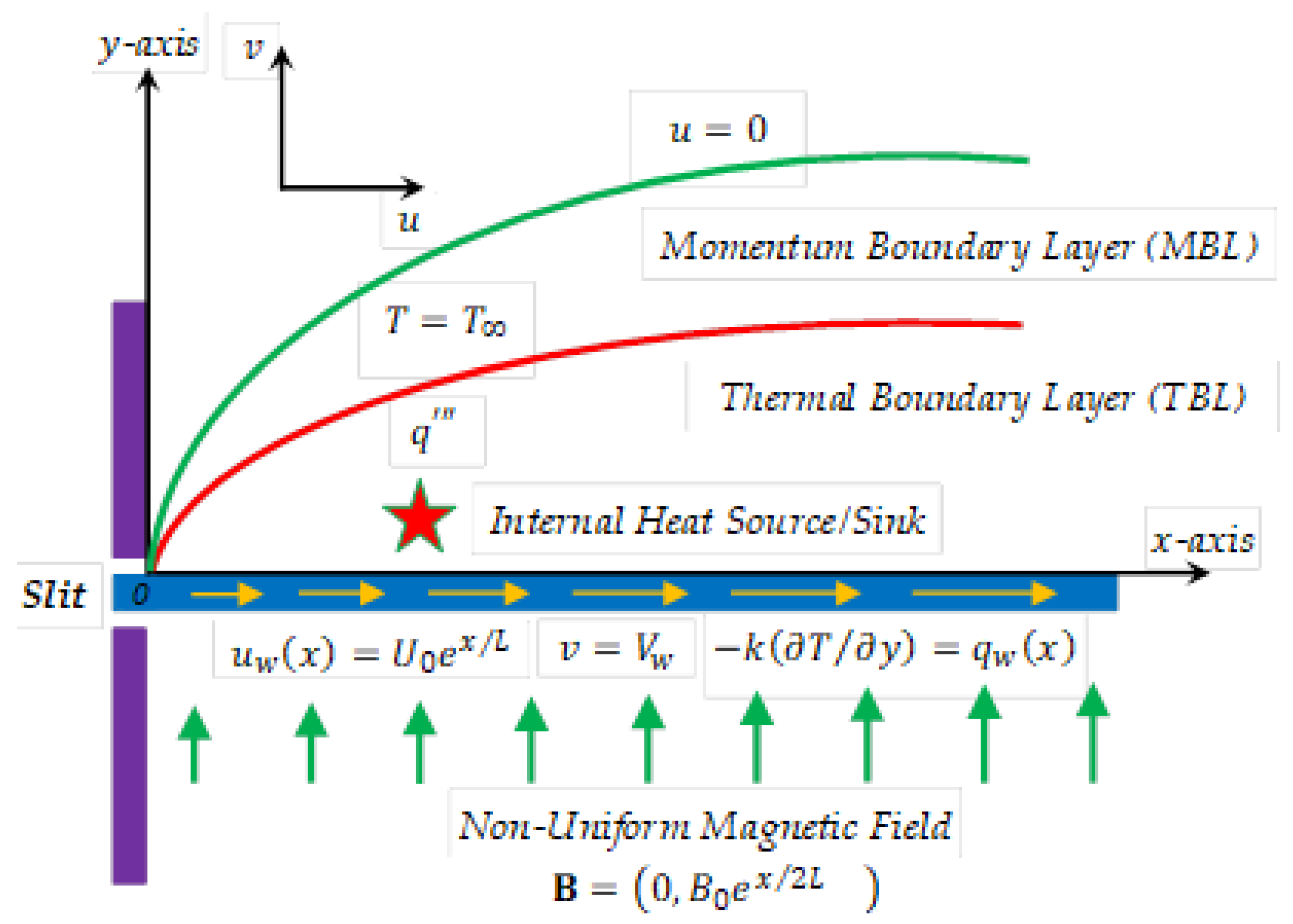
2. Definition of the Problem
3. Relevant Physical Measures
4. Entropy Generation and Bejan Number
5. Solution Methodology and Validation of Results
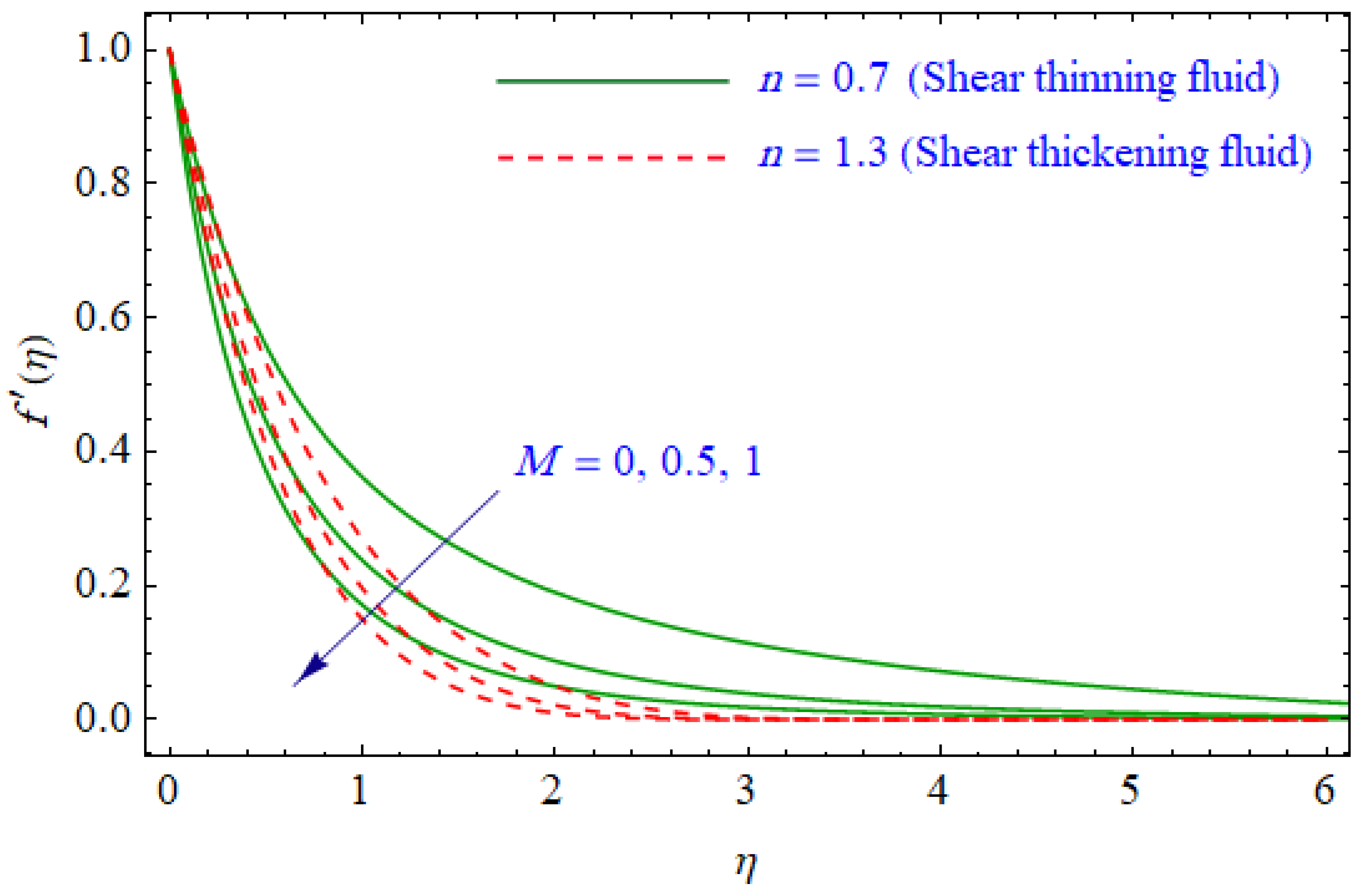
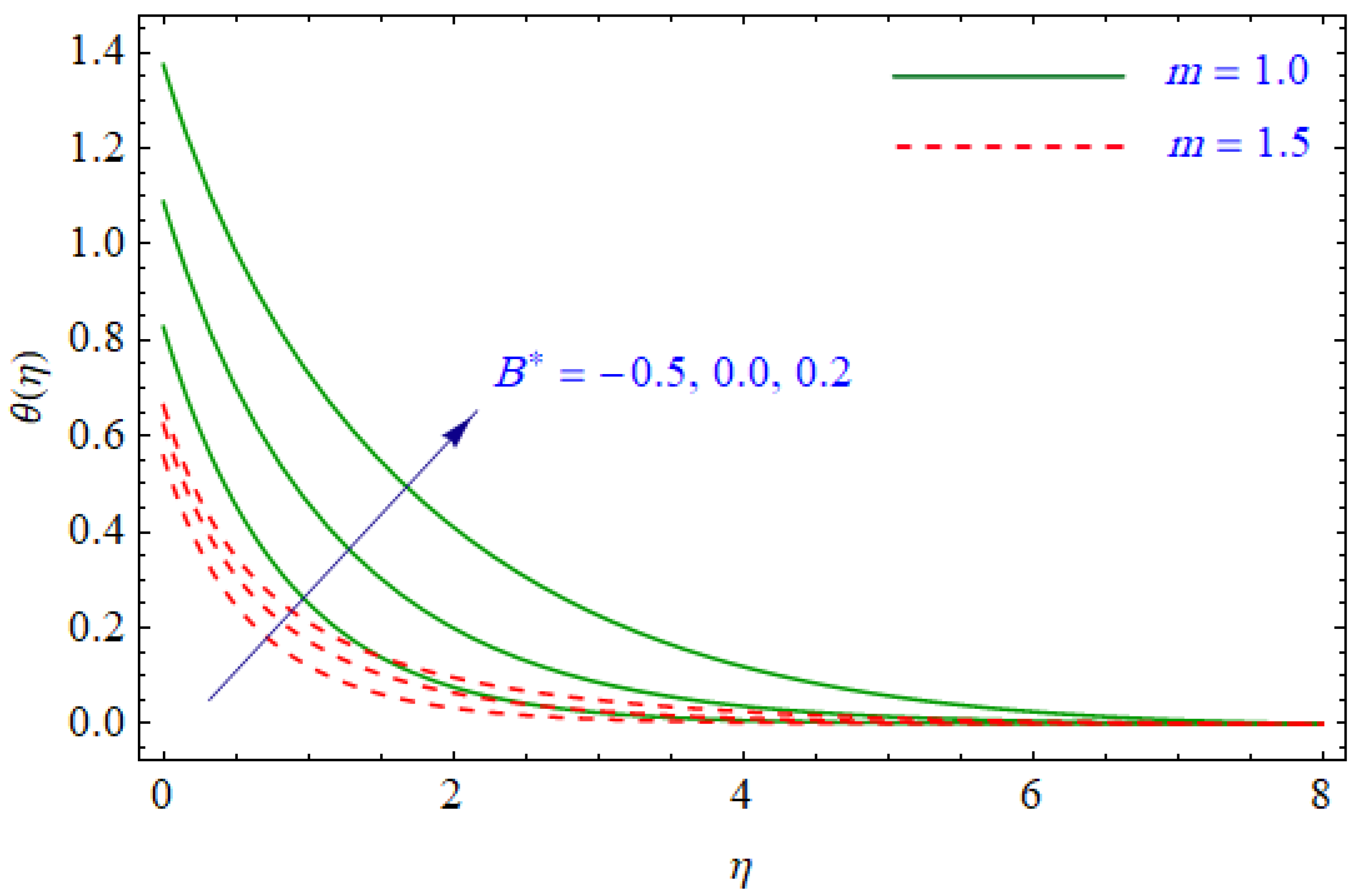
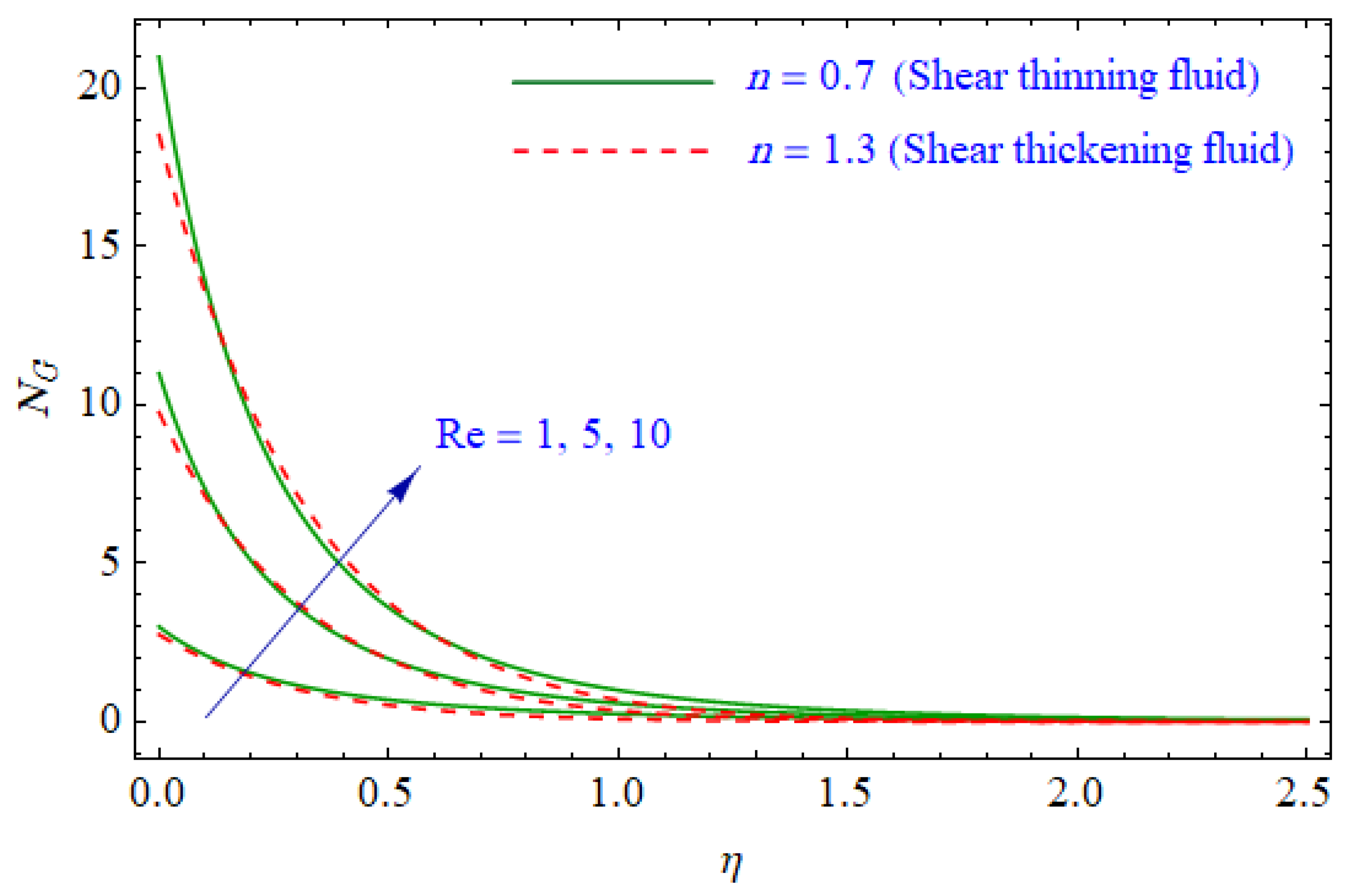
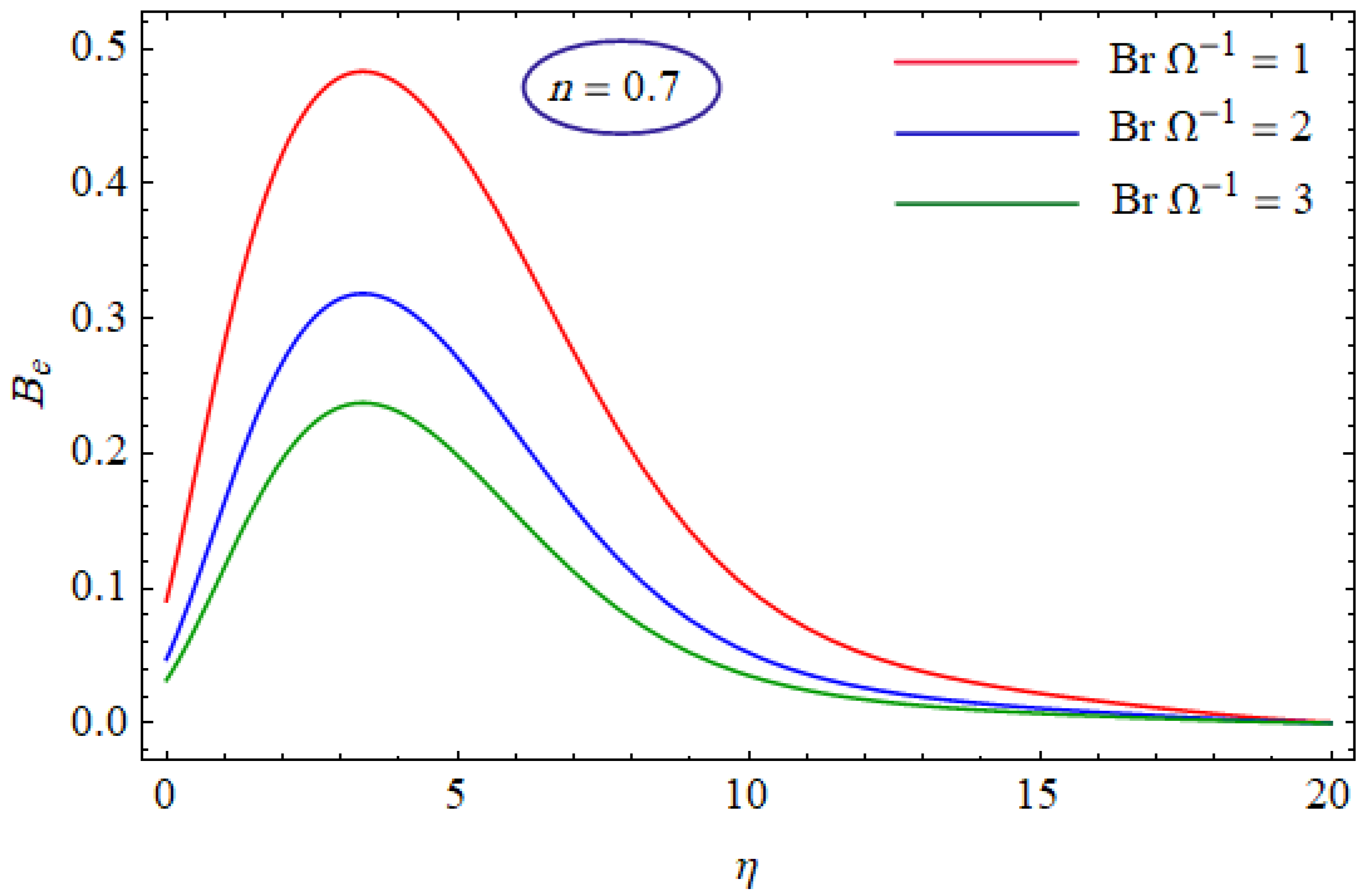
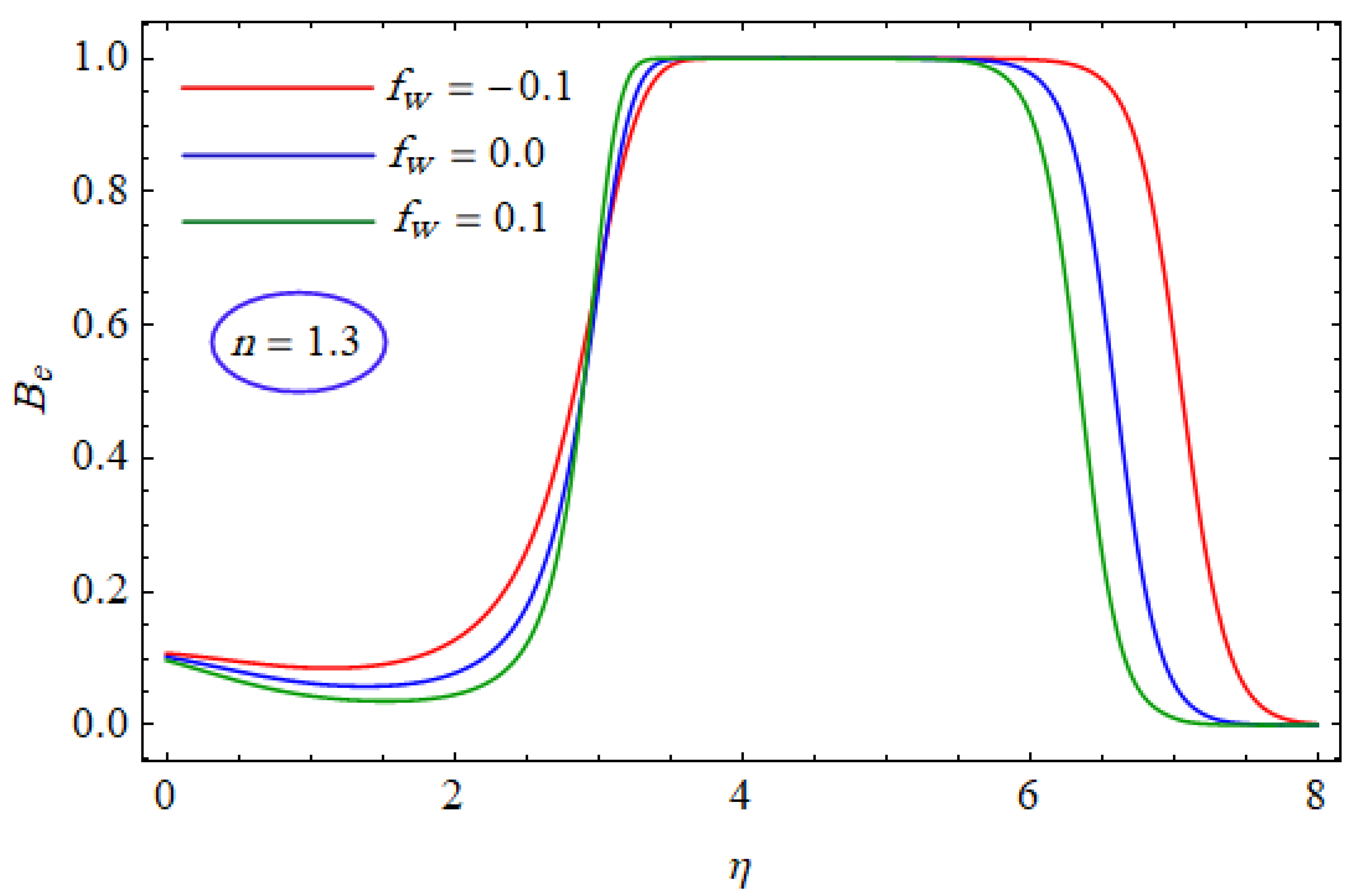
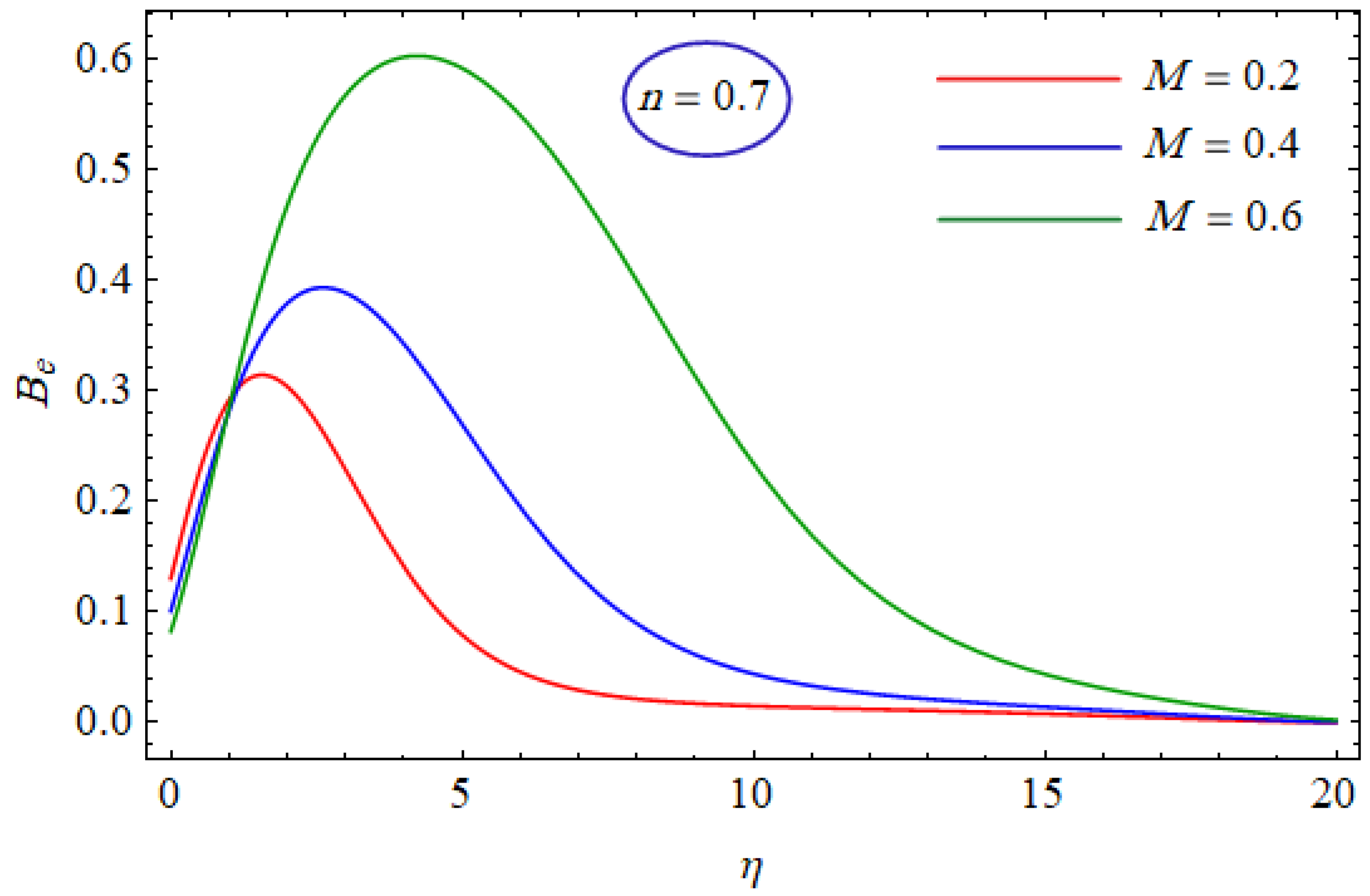
6. Results and Discussion
7. Conclusions
- The Bejan number expressively decreased and the total entropy generation was augmented with the growing Reynolds number.
- The quality of energy reduces, i.e., entropy generation is enhanced, with large magnetic and group parameters.
- The velocity of the power-law fluid varies indirectly with the suction/injection parameter.
- The heat transfer rate decay under the presence of an internal heat source and magnetic field was established.
- Thermal boundary layer decreases with an increasing heat flux index during the phenomenon.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Willey: New York, NY, USA, 1982. [Google Scholar]
- Kaushik, P.; Mondal, K.P.; Pati, S.; Chakraborty, S. Heat transfer and entropy generation characteristics of a non-Newtonian fluid squeezed and extruded between two parallel plates. J. Heat Transf. 2017, 139, 022004. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Darzi, M.; Li, Z. Experimental investigation for entropy generation and exergy loss of nano-refrigerant condensation process. Int. J. Heat Mass Transf. 2018, 125, 1087–1095. [Google Scholar] [CrossRef]
- Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Second law analysis of dissipative nanofluid flow over a curved surface in the presence of Lorentz force: Utilization of the Chebyshev-Gauss-Lobatto spectral method. Nanomaterials 2019, 9, 195. [Google Scholar] [CrossRef] [PubMed]
- Nouri, D.; Pasandideh-Fard, M.; Oboodi, M.J.; Mahian, O.; Sahin, A.Z. Entropy generation analysis of nanofluid flow over a spherical heat source inside a channel with sudden expansion and contraction. Int. J. Heat Mass Transf. 2018, 116, 1036–1043. [Google Scholar] [CrossRef]
- Dormohammadi, R.; Farzaneh-Gord, M.; Ebrahimi-Moghadam, A.; Ahmadi, M.H. Heat transfer and entropy generation of the nanofluid flow inside sinusoidal wavy channels. J. Mol. Liq. 2018, 269, 229–240. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ Model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy 2013, 55, 497–510. [Google Scholar] [CrossRef]
- Liu, Y.; Jian, Y.; Tan, W. Entropy generation of electromagnetohydrodynamic (EMHD) flow in a curved rectangular microchannel. Int. J. Heat Mass Transf. 2018, 127, 901–913. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat. Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Rehman, A.U.; Mehmood, R.; Nadeem, S. Entropy analysis of radioactive rotating nanofluid with thermal slip. Appl. Therm. Eng. 2017, 112, 832–840. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Rashidi, S.; Karimi, N.; Ellahi, R. Convection of heat and thermodynamic irreversibilities in two-phase, turbulent nanofluid flows in solar heaters by corrugated absorber plates. Adv. Powder Technol. 2018, 29, 2243–2254. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I.; Wakif, A.; Thoi, T.N.; Hussanan, A. Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method. Entropy 2019, 21, 240. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Saleem, S. Second law analysis of three dimension dissipative flow of Hybrid nanofluid. J. Nanofluids 2018, 7, 1272–1280. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sustain. Energy Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Makinde, O.D.; Osalusi, E. ESecond law analysis of laminar flow in a channel filled with saturated porous media. Entropy 2005, 7, 148–160. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Khan, I.; Al-Mdallal, Q.M. Analysis of entropy generation in flow of methanol-based nanofluid in a sinusoidal wavy channel. Entropy 2017, 19, 490. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Scott, S.H.; Abt, S.R. Hydraulic transport of fine and coarse sediment mixtures in pipelines. J. Transp. Eng. 2002, 128, 1–8. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Khan, A.U.; Saleem, S.; Nadeem, S. Numerical simulation of oscillatory oblique stagnation point flow of a magneto micropolar nanofluid. RSC Adv. 2019, 9, 4751–4764. [Google Scholar] [CrossRef]
- Saleem, S.; Firdous, H.; Nadeem, S.; Khan, A.U. Convective heat and mass transfer in magneto Walter’s B nanofluid flow induced by a rotating cone. Arab. J. Sci. Eng. 2019, 44, 1515–1523. [Google Scholar] [CrossRef]
- Malik, M.Y.; Salahuddin, T.; Hussain, A.; Bilal, S. MHD flow of tangent hyperbolic fluid over a stretching cylinder: Using Keller box method. J. Magn. Magn. Mater. 2015, 395, 271–276. [Google Scholar] [CrossRef]
- Sadaf, H.; Akbar, M.U.; Nadeem, S. Induced magnetic field analysis for the peristaltic transport of non-Newtonian nanofluid in an annulus. Math. Comput. Simul. 2018, 148, 16–36. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Saleem, S.; Al-Qarni, M.M.; Mamatha Upadhya, S. Unsteady nonlinear convection on Eyring-Powell radiated flow with suspended graphene and dust particles. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
- Haque, A.; Nayak, A.K.; Soni, B.; Majhi, M. Thermosolutal hydromagnetic convection of power-law fluids in an enclosure with periodic active zones. Int. J. Heat Mass Transf. 2018, 127C, 622–642. [Google Scholar] [CrossRef]
- El-Aziz, M.A.; Afify, A.A. Lie group analysis of hydromagnetic flow and heat transfer of a power-law fluid over stretching surface with temperature-dependent viscosity and thermal conductivity. Int. J. Mod. Phys. C 2016, 27, 1650150. [Google Scholar] [CrossRef]
- Sasmal, C.; Gupta, A.K.; Chhabra, R.P. Natural convection heat transfer in a power-law fluid from a heated rotating cylinder in a square duct. Int. J. Heat Mass Transf. 2019, 129, 975–996. [Google Scholar] [CrossRef]
- Salem, A.M.; El-Aziz, M.A.; Abo-Eldahab, E.M.; Abd-Elfatah, I. Effect of variable density on hydromagnetic mixed convection flow of a non-Newtonian fluid past a moving vertical plate. Commun. Nonlinear Sci. Numer. Simul. 2009, 15, 1485–1493. [Google Scholar] [CrossRef]
- Mohebbi, R.; Nazari, M.; Kayhani, M. Comparative study of forced convection of a power-law fluid in a channel with a built-in square cylinder. J. Appl. Mech. Technol. Phys. 2016, 57, 55–68. [Google Scholar] [CrossRef]
- El-Aziz, M.A.; Yahya, A.S. Heat and Mass Transfer of Unsteady Hydromagnetic Free Convection Flow Through Porous Medium Past a Vertical Plate with Uniform Surface Heat Flux. J. Theor. Appl. Mech. 2017, 47, 25–58. [Google Scholar] [CrossRef]
- Metri, P.G.; Metri, P.G.; Abel, S.; Silvestrov, S. Heat transfer in MHD mixed convection viscoelastic fluid flow over a stretching sheet embedded in a porous medium with viscous dissipation and non-uniform heat source/sink. Procedia Eng. 2016, 157, 309–316. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Rashidi, S. Modelling Study on Internal Energy Loss Due to Entropy Generation for Non-Darcy Poiseuille Flow of Silver-Water Nanofluid: An Application of Purification. Entropy 2018, 20, 851. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Flow of 3D Eyring-Powell fluid by utilizing Cattaneo-Christov heat flux model and chemical processes over an exponentially stretching surface. Results Phys. 2018, 8, 397–403. [Google Scholar] [CrossRef]
- Patil, P.M.; Latha, D.N.; Roy, S. Ebrahim Momoniat, Double diffusive mixed convection flow from a vertical exponentially stretching surface in presence of the viscous dissipation. Int. J. Heat Mass Transf. 2017, 112, 758–766. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz Khan, M.; Farooq, M.; Alsaedi, A.; Waqas, M. Tabassam Yasmeen, Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Nadeem, S.; Lee, C. Boundary layer flow of nanofluid over an exponentially stretching surface. Nanoscale Res. Lett. 2012, 7, 94. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M.; Khan, W.A. Impact of non-uniform heat sink/source and convective condition in radiative heat transfer to Oldroyd-B nanofluid: A revised proposed relation. Phys. Lett. A 2019, 383, 376–382. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Mahanthesh, B.; Jagun, A.O.; Bankole, T.D.; Sivaraj, R.; Shah, N.A.; Saleem, S. Significance of Lorentz Force and Thermoelectric on the Flow of 29 nm CuO–Water Nanofluid on an Upper Horizontal Surface of a Paraboloid of Revolution. J. Heat Transf. 2019, 141, 022402. [Google Scholar] [CrossRef]
- Saleem, S.; AlQarni, M.M.; Nadeem, S.; Sandeep, N. Convective heat and mass transfer in magneto Jeffrey fluid flow on a rotating cone with heat source and chemical reaction. Commun. Theor. Phys. 2018, 70, 534–540. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz Khan, M.; Farooq, M.; Yasmeen, T.; Alsaedi, A. Stagnation point flow with Cattaneo-Christov heat flux and homogeneous-heterogeneous reactions. J. Mol. Liq. 2016, 220, 49–55. [Google Scholar] [CrossRef]
- Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy 2018, 20, 943. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 1–27. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of Radiative Electro-Magnetohydrodynamics Diminishing Internal Energy of Pressure-Driven Flow of Titanium Dioxide-Water Nanofluid due to Entropy Generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Saleem, S.; Wakif, A.; AlQarni, M.M. MHD Prandtl fluid flow past an isothermal permeable sphere with slip effects. Case Stud. Therm. Eng. 2019, 14, 100447. [Google Scholar] [CrossRef]
- Makinde, O.D.; Omojola, M.T.; Mahanthesh, B.; Alao, F.I.; Adegbie, K.S.; Animasaun, I.L.; Wakif, A.; Sivaraj, R.; Tshehla, M.S. Significance of Buoyancy, Velocity Index and Thickness of an Upper Horizontal Surface of a Paraboloid of Revolution: The Case of Non-Newtonian Carreau Fluid. Defect. Diffus. Forum 2018, 387, 550–561. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I.; Wakif, A.; Saleem, S. Influence of Variable Transport Properties on Nonlinear Radioactive Jeffrey Fluid Flow Over a Disk: Utilization of Generalized Differential Quadrature Method. Arab. J. Sci. Eng. 2019, 1–10. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Mishra, S.R.; Mehdi Rashidi, M.; Sehaqui, R. Influence of a uniform transverse magnetic field on the thermo-hydrodynamic stability in water-based nanofluids with metallic nanoparticles using the generalized Buongiorno’s mathematical model. Eur. Phys. J. Plus. 2018, 133, 181. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. A Semi-Analytical Analysis of Electro-Thermo-Hydrodynamic Stability in Dielectric Nanofluids Using Buongiorno’s Mathematical Model Together with More Realistic Boundary Conditions. Results Phys. 2018, 9, 1438–1454. [Google Scholar] [CrossRef]
- Saleem, S.; Nadeem, S.; Rashidi, M.M.; Raju, C.S.K. An optimal analysis of radiated nanomaterial flow with viscous dissipation and heat source. Microsyst. Technol. 2019, 25, 683–689. [Google Scholar] [CrossRef]
- Saleem, S.; El-Aziz, M.A. Entropy generation and convective heat transfer of radiated non-Newtonian power-law fluid past an exponentially moving surface under slip effects. Eur. Phys. J. Plus. 2019, 134, 184. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Wakif, A.; Boulahia, Z.; Fazuruddin, S.; Mohammed, S.N. A Study on Non-Newtonian Transport Phenomena in MHD Fluid Flow from a Vertical Cone with Navier Slip and Convective Heating. Nonlinear Eng. 2019, 8, 534–545. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Amine, A.; Animasaun, I.L.; Afridi, M.I.; Qasim, M.; Sehaqui, R. Magneto-Convection of Alumina—Water Nanofluid Within Thin Horizontal Layers Using the Revised Generalized Buongiorno’s Model. Front. Heat Mass Transf. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Amanulla, C.H.; Wakif, A.; Boulahia, Z.; Suryanarayana Reddy, M.; Nagendra, N. Numerical investigations on magnetic field modeling for Carreau non-Newtonian fluid flow past an isothermal sphere. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 462. [Google Scholar] [CrossRef]
- Cimpean, D.; Lungu, N.; Pop, I. A problem of entropy generation in a channel filled with a porous medium. Creative Math. Inform. 2008, 17, 357–362. [Google Scholar]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577–585. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over an exponentially stretching continuous surface with suction. Arc. Mech. 2001, 53, 643–651. [Google Scholar]
- Sahoo, B.; Poncet, S. Flow and heat transfer of a third grade fluid past an exponentially stretching sheet with partial slip boundary condition. Int. J. Heat Mass Transf. 2011, 54, 5010–5019. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Moindal, I.C.; Hayat, T. MHD boundary layer flow of Casson fluid passing through an exponentially stretching permeable surface with thermal radiation. Chin. Phys. B 2014, 23, 104701. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]















| Existing Results for | Present Result for | ||||
|---|---|---|---|---|---|
| [56] | [57] | [58] | [59] | [60] | SRKFM |
| −1.28180 | −1.28181 | −1.281811 | −1.281812 | −1.28181 | −1.2818098 |
| M | ||||||
|---|---|---|---|---|---|---|
| 0.0 | −1.264728 | 0.957247 | ||||
| 0.5 | 0.0 | 1.0 | 0.1 | 0.1 | −1.570997 | 0.836066 |
| 1.0 | −1.808090 | 0.731285 | ||||
| −0.3 | −1.513345 | 0.625733 | ||||
| 0.5 | 0.1 | 1.0 | 0.1 | 0.1 | −1.590886 | 0.913095 |
| 0.3 | −1.631743 | 1.075468 | ||||
| 0.8 | −1.570988 | 0.441335 | ||||
| 0.5 | 0.0 | 1.5 | 0.1 | 0.1 | −1.571019 | 1.556417 |
| 3.0 | −1.571019 | 2.930572 | ||||
| −0.5 | −1.570997 | 1.171080 | ||||
| 0.5 | 0.0 | 0.1 | 0.0 | 0.1 | −1.570997 | 0.891902 |
| 0.5 | −1.570997 | 0.441335 | ||||
| −0.5 | −1.570997 | 1.208040 | ||||
| 0.5 | 0.0 | 0.1 | 0.1 | 0.0 | −1.570997 | 0.918485 |
| 0.2 | −1.570997 | 0.727479 |
| M | ||||||
|---|---|---|---|---|---|---|
| 0.0 | −1.313498 | 1.956119 | ||||
| 0.5 | 0.0 | 1.0 | 0.1 | 0.1 | −1.679224 | 1.883365 |
| 1.0 | −1.992612 | 1.822293 | ||||
| −0.3 | −1.470333 | 1.354459 | ||||
| 0.5 | 0.1 | 1.0 | 0.1 | 0.1 | −1.754932 | 2.089481 |
| 0.3 | −1.915439 | 2.546558 | ||||
| 0.8 | −1.679185 | 1.668265 | ||||
| 0.5 | 0.0 | 1.5 | 0.1 | 0.1 | −1.679185 | 2.355932 |
| 3.0 | −1.679185 | 3.474166 | ||||
| −0.5 | −1.679185 | 2.099785 | ||||
| 0.5 | 0.0 | 0.1 | 0.0 | 0.1 | −1.679185 | 1.917798 |
| 0.5 | −1.679185 | 1.735811 | ||||
| −0.5 | −1.679185 | 2.060122 | ||||
| 0.5 | 0.0 | 0.1 | 0.1 | 0.0 | −1.679185 | 1.913069 |
| 0.2 | −1.679185 | 1.848783 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd El-Aziz, M.; Saleem, S. Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux. Entropy 2019, 21, 484. https://doi.org/10.3390/e21050484
Abd El-Aziz M, Saleem S. Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux. Entropy. 2019; 21(5):484. https://doi.org/10.3390/e21050484
Chicago/Turabian StyleAbd El-Aziz, Mohamed, and Salman Saleem. 2019. "Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux" Entropy 21, no. 5: 484. https://doi.org/10.3390/e21050484
APA StyleAbd El-Aziz, M., & Saleem, S. (2019). Numerical Simulation of Entropy Generation for Power-Law Liquid Flow over a Permeable Exponential Stretched Surface with Variable Heat Source and Heat Flux. Entropy, 21(5), 484. https://doi.org/10.3390/e21050484





