Abstract
In the present article, fractional-order diffusion equations are solved using the Natural transform decomposition method. The series form solutions are obtained for fractional-order diffusion equations using the proposed method. Some numerical examples are presented to understand the procedure of the Natural transform decomposition method. The Natural transform decomposition method has shown the least volume of calculations and a high rate of convergence compared to other analytical techniques, the proposed method can also be easily applied to other non-linear problems. Therefore, the Natural transform decomposition method is considered to be one of the best analytical technique, to solve fractional-order linear and non-linear partial deferential equations, particularly fractional-order diffusion equation.
1. Introduction
The idea of fractional calculus and entropy are attractive and more prevalent for investigating the dynamics of complex systems. In modern years, fractional calculus (FC) has been progressively applied in various fields of science. Natural development identified with viscoelasticity, models of porous electrodes, thermal stresses, electromagnetism, propagation of energy in dissipative systems, relaxation vibrations, and thermoelasticity are effectively portrayed by fractional differential equations (FDE’s) [1]. The knowledge of entropy was presented in the field of thermodynamics by Clausius (1862) and Boltzmann (1896) and was further applied by Shannon (1948) and Jaynes (1957) in information theory. Newly, more universal entropy measures have being suggested for applications in numerous varieties of complex systems, outstanding to the relaxation of the additive axiom [2]. The idea of entropy for calculating the dynamics of multi-particle systems with integer- and fractional-order behavior was suggested in [3]. The entropy production rate for the fractional diffusion procedure was considered in [4]. In [5], it has been shown that the total spectral entropy can be used as a measure of the data, comfortable in a fractional-order model of anomalous diffusion. Entropies based on fractional calculus [6]. Feng’s first integral method was applied successfully to obtain nonlinear space-time fractional modified Korteweg–de Vries equations [7], nonlinear partial differential equations, third-order dispersion [8,9] in entropy and convexity, fractional derivative advection-diffusion in two-dimensional semi-conductor systems, and the dynamics of a national soccer league [10]. The exact solution to differential equations (DEs) of fractional-order with mixed partial derivatives [11] and space-fractional diffusion equation and Tsallis relative entropy [12]. Diffusion forms contrast from regular diffusion in that the scattering of particles continues quicker (super diffusion) or slower (sub diffusion) than for the ordinary case.
Adolf Fick described Fick’s laws of diffusion in 1885. After that, Fick’s second law became known as the diffusion equation. Diffusion is the mesh movement of atoms or molecules from an area of higher concentration or great chemical potential to an area of inferior concentration or small chemical potential. In [13], the researchers generalized the classical diffusion and wave equations—different physical process such as classical diffusion, slow diffusion, the classical wave equation, and diffusion-wave hybrid. Many applications of diffusion equation, such as electrochemistry, phase transition, filtration, electromagnetism, acoustics, biochemistry, cosmology, and dynamics of biological groups [14]. Diffusion is determined by a gradient in chemical potential of the diffusing types. A gradient is the variation in the value of a number, e.g., concentration, pressure, or temperature with the variation in one or more variables being frequently distinct. A variation in temperature ended with a distance is called a temperature gradient, a variation in concentration over a distance is called a concentration gradient, and a variation in pressure ended with a distance is called a pressure gradient. Scientists have been attempting to comprehend and diminish the challenges of industrial procedures to accomplish higher effectiveness [15]. In engineering systems, there are different causes for entropy generation. In thermal systems, the primary source of entropy generation is mass transfer, heat transfer, viscous dissipation, coupling among heat, electrical conduction, and chemical reaction, as examined in a pioneering series of publications by Bejan and co-workers [16,17]. Researchers have used various techniques for the solution of diffusion equations such as the Collocation method (CM) [18], Diffusion and Tsallis entropy [19], Entropy production, Symmetric fractional diffusion [20], Finite differences method in space-fractional diffusion equations [21,22,23], Homotopy analysis method (HAM) [24], Homotopy perturbation transform method (HPTM) [25] and Modified homotopy perturbation method (MHPM) [26], Mehshless method (MM) [27], One-Dimensional alpha fractional diffusion [28], Radial basis function method (RBFM) [29], and the Variational iteration method (VIM) [30].
In the present work, we are applying the Natural transform decomposition method (NTDM) to solve the following types of diffusion equations.
- (1)
- Two-dimensional fractional-order diffusion equation of the form:subject to the initial condition
- (2)
- Three-dimensional fractional-order diffusion equation is given bysubject to the initial condition
Natural transform and the Adomain decomposition method are two powerful methods that have been used to develop the Natural transform decomposition method. Many physical phenomena that are modeled by PDEs and FPDEs are solved using NTDM, such as the analytical solution of a coupled system of non-linear PDEs, are suggested in [31], the solution non-linear ODEs are successfully presented in [32], non-linear PDEs in [33], fractional unsteady flow of a polytropic gas model in [34], fractional telegraph equations in [35], and the fractional Fokker–Plank equation and Schrödinger equation in [36]. The accuracy of the proposed method is compared with the solutions obtained by HPM and MHPM. The comparisons have shown that the proposed method has a higher rate of convergence than HPM and MHPM. The rest of the article is structured as follows: In Section 2, we recall several basic properties and define Natural transform and fractional calculus. In Section 3, the idea of Natural transform decomposition method is discussed. In Section 4, we explain many problems to maintaining the accuracy and efficiency of the proposed method, and Section 5 is devoted to the conclusion.
2. Preliminaries
Definition 1.
The natural transform of is defined as [37,38]
where s and u are the transform variables.
Definition 2.
The inverse natural transform of a function is defined by
where s and u are the Natural transform variables, p is a real constant, and the integral is taken along in the complex plane .
Definition 3.
Natural Transform of n-th Derivative
If is the n-th derivative of function , it is given by
Theorem 1.
If and are the transform functions and , respectively, they are given by,
where is the convolution of two functions h and l.
Definition 4.
R–L fractional integral
where Γ denotes the gamma function, defined by
In their study, Caputo et al. suggested a revised fractional derivative operator in order to overcome inconsistencies measured in the Riemann–Liouville derivative. The above mathematical statement described a Caputo fractional derivative operator of initial and boundary condition for fractional—as well as integer-order derivatives [39,40].
Definition 5.
The Caputo operator of order γ for a fractional derivative is given by the following mathematical expression for , , , [41]:
Definition 6.
TheMittag–Leffler function for is defined by the following subsequent series
Theorem 2.
Here, we will study the convergence analysis, in the same manner as in [42], of the NTDM applied to the fractional dispersive PDE of order three. Let us consider the Hilbert space H, which may defined by the set of applications:
Now we consider the fractional-order of diffusion equations of order three in the above assumptions which lets us denote
then the fractional-order of diffusion equations becomes, in an operator form,
The NTDM reaches convergence if the following two hypotheses are satisfied:
whatever may be , there exist a constant such that for with , we have for every .
3. Idea of Fractional Natural Transform Decomposition Method
In this section, we use the Natural transform decomposition method to find the general solution fractional-order diffusion equations.
where is the Caputo Operator , L and N are respectively linear and non-linear functions, and q is the source function.
The initial condition is
Applying the Natural transform to Equation (1), we have
and using the differentiation property of Natural transform, we get
Now ,
The NTDM solution is represented by the following infinite series:
and the non-linear terms (if any) in the problem are defined by the infinite series of Adomian polynomials
substituting Equations (5) and (6) into Equation (4), we get
Applying the linearity of the Natural transform,
Generally, we can write
Applying the inverse Natural transform, Equations (9) and (10)
4. Results
4.1. Example
Consider the two-dimensional fractional diffusion equation [26]:
with the initial condition
Taking the Natural transform of Equation (12),
Applying inverse Natural transform, we get
Using the ADM procedure, we get
for :
The subsequent terms are
The NTDM solution for Example 4.1 is:
When , the NTDM solution is
This result is calculated to the exact solution in a closed form:
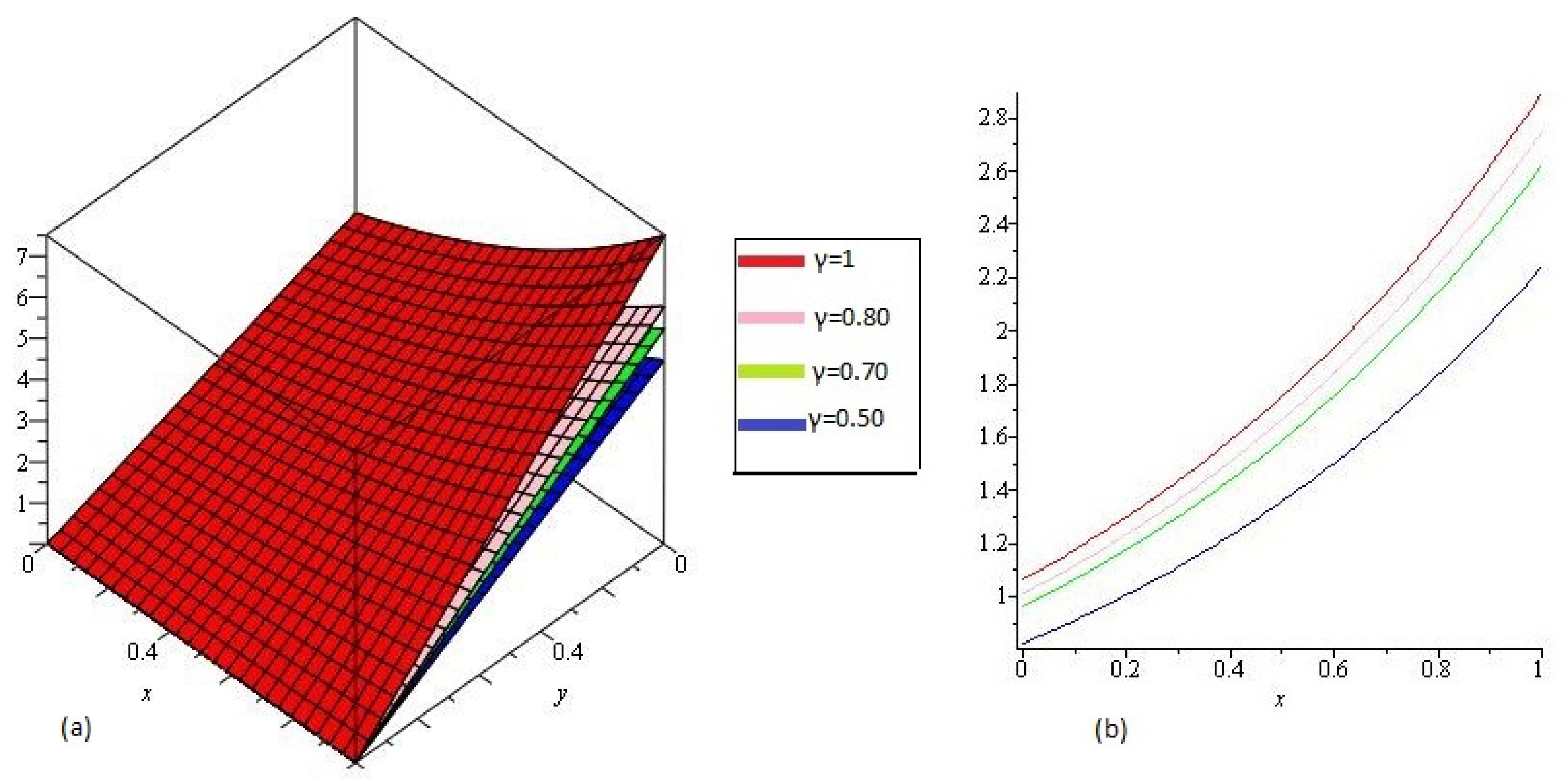
In Figure 1 NTDM solution of Example 4.1 of different value of , , and and are represented by Figure 1a and Figure 1b respectively at y, and . From the given graphs it can be observed that both exact and NTMD solutions are in strong agrement with each other.
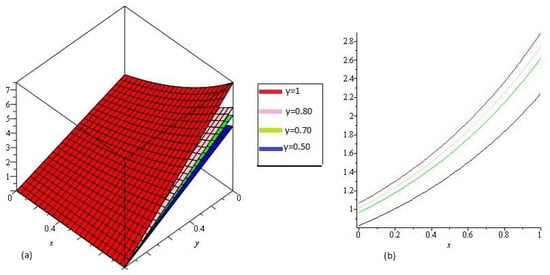
Figure 1.
The (a) NTDM of of Example 4.1, for different value of and (b) .
4.2. Example
Consider the two-dimensional fractional diffusion equation [26]:
with the initial condition
Taking the Natural transform of Equation (18):
Applying inverse Natural transform, we get
Using ADM procedure, we get
for :
The NTDM solution for Example 4.2 is
When , then the NTDM solution is
This result is calculated to the exact solution in a closed form:
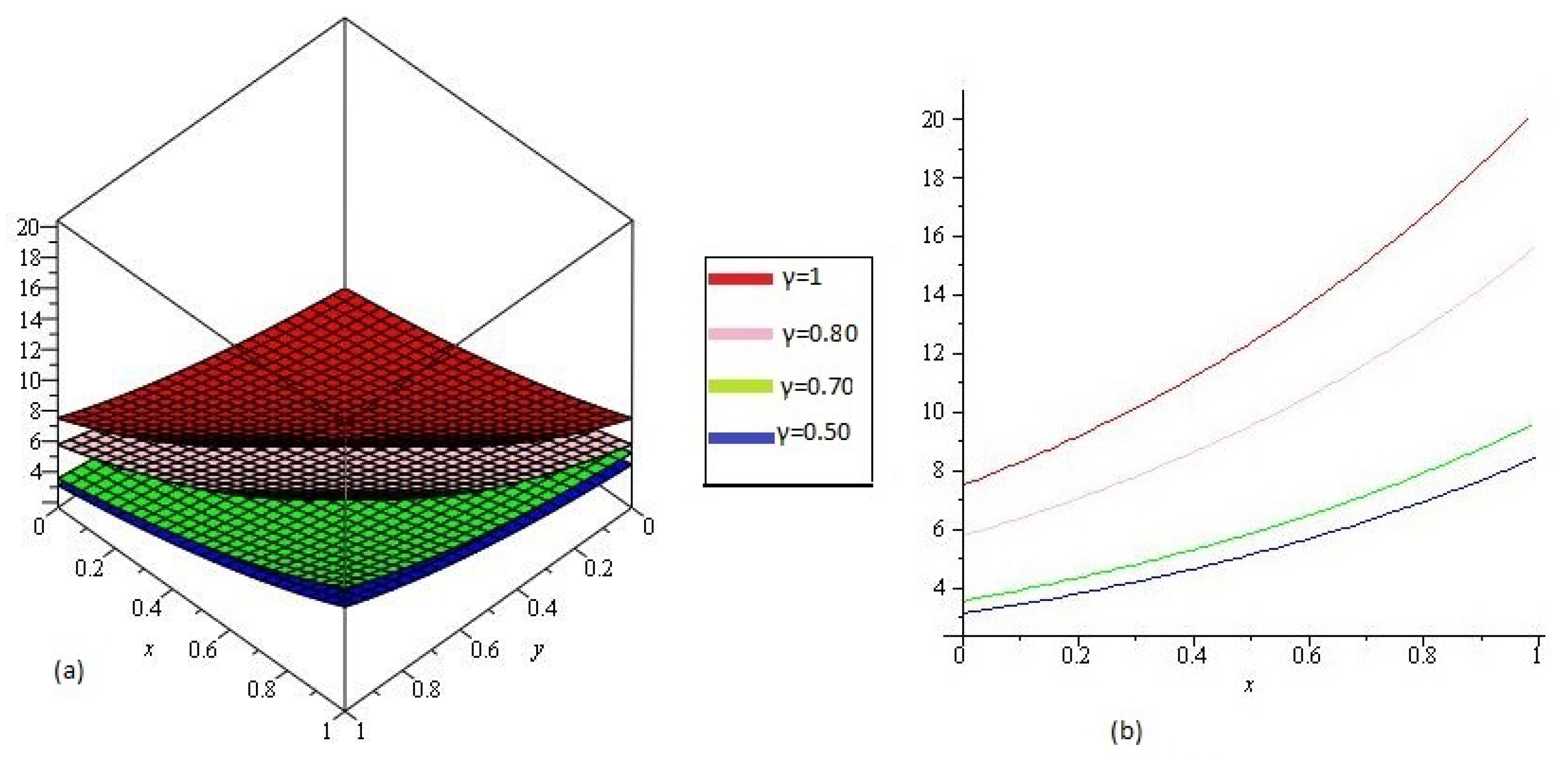
In Figure 2 NTDM solution of Example 4.2 of different value of , , and and are represented by Figure 2a and Figure 2b respectively at y, and . From the given graphs it can be observed that both exact and NTDM solutions are in strong agrement with each other.
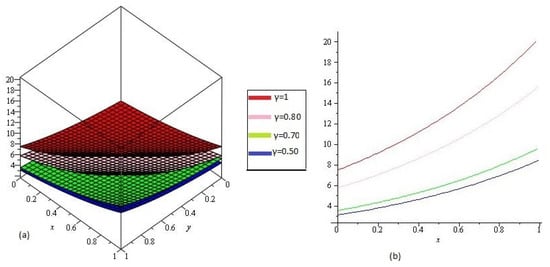
Figure 2.
The (a) NTDM solutions of of Example 4.2, for different values of and (b) .
4.3. Example
Consider the three-dimensional fractional diffusion equation [25]:
with the initial condition
Taking the Natural transform of Equation (24),
Applying inverse Natural transform, we get
Using ADM procedure, we get
for :
The subsequent terms are:
The NTDM solution for Example 4.3 is
When , then the NTDM solution is
This result is calculated to the exact solution in a closed form:
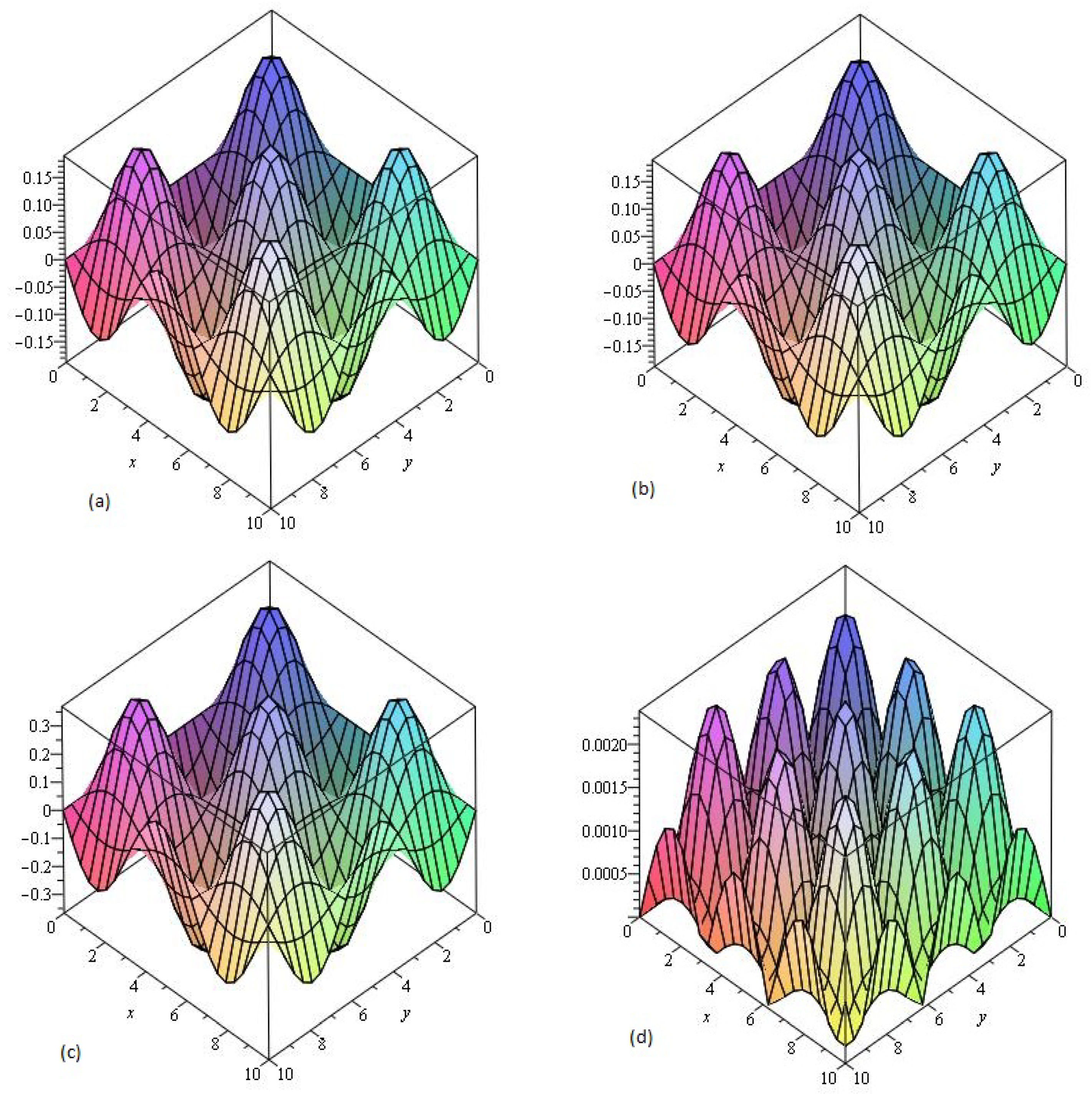
Similarly, in Figure 3 the numerical values of the Example 4.3 show the accuracy and efficiency of the NTDM at different values of . In Figure 3a,b we consider fixed order for piecewise approximation values of in the domain . Figure 3c represents the graphs of NTDM solution at , and error Figure 3d at respectively of Example 4.3. It is cleared from the Figure 3a,b that NTDM solution are in good agreement with the exact solution of the problems. The small difference from the solutions graph of the problem, because the solution of the fractional-order problems creates a little deviation from the solution at integer order problem.
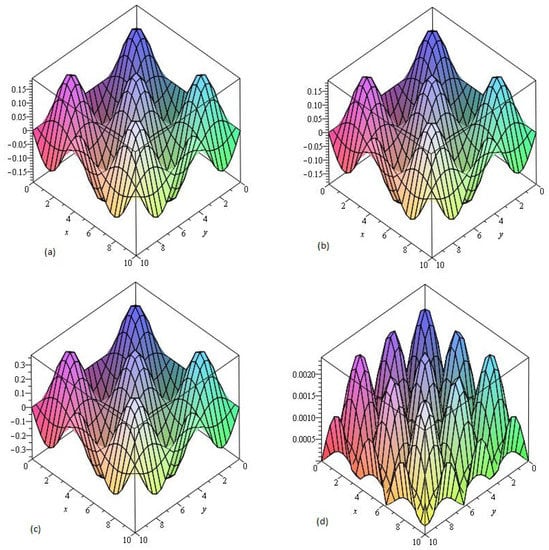
Figure 3.
The (a) Exact and (b) NTDM solutions of of Example 4.3, at , (c) at and (d) Error plot at .
5. Conclusions
In this paper, the analytical solutions of fractional-order diffusion equations are determined, using NTDM. The NTDM solutions are obtained at fractional and integer orders for all problems. The results revealed the highest agreement with the exact solutions for the problems. The NTDM solutions for some numerical examples have shown the validity of the proposed method. It is also investigated that the fractional-order solutions are convergent to the exact solution for the problems as fractional-order approaches integer-order. The implementation of NTDM to illustrative examples have also confirmed that the fractional-order mathematical model can be the best representation of any experimental data compared to the integer-order model. Moreover, by taking different fractional orders, we can find a way to set a suitable mathematical model for any experimental data, and thus find reasonable consequences. Hence, it is concluded that NTDM is the best tool for the solution of FPDEs compared to ADM, VIM, and DTM discussed in literature. NTDM provides the highest rate of convergence to the exact solution for the problems. In the future, NTDM can be used to find the analytical solution of other non-linear FPDEs, which are frequently used in science and engineering. NTDM solutions for fractional-order problems will prove the best understanding of the real world problems represented by FPDEs.
Author Contributions
Conceptualization, R.S. and H.K.; Methodology, M.A.; Software, R.S.; Validation, S.M. and M.A.; Formal Analysis, R.S.; Investigation, R.S. and P.K.; Resources, H.K. and P.K.; Data Curation, R.S.; Writing—Original Draft Preparation, R.S.; Writing—Review and Editing, H.K., M.A. and P.K.; Visualization, M.A.; Supervision, M.A., P.K.; Project Administration, P.K.; Funding Acquisition, P.K.
Funding
The project was supported by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT).
Acknowledgments
This project was supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
Conflicts of Interest
The authors have no conflict of interest.
References
- Gómez-Aguilar, J.F.; Atangana, A. Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann-Liouville and Liouville-Caputo sense. Eur. Phys. J. Plus 2017, 132, 100. [Google Scholar] [CrossRef]
- Arshad, S.; Baleanu, D.; Huang, J.; Al Qurashi, M.; Tang, Y.; Zhao, Y. Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative. Entropy 2018, 20, 321. [Google Scholar] [CrossRef]
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilib. Thermodyn. 1998, 23, 166–175. [Google Scholar] [CrossRef]
- Magin, R.L.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. IFAC Proc. 2012, 45, 428–433. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Gómez-Aguilar, F.; Sosa, I.O.; Reyes, J.M.; Torres-Jiménez, J. The Feng’s first integral method applied to the nonlinear mKdV space-time fractional partial differential equation. Rev. Mex. Fís. 2016, 62, 310–316. [Google Scholar]
- Ball, J.M.; Chen, G.Q.G. Entropy and convexity for nonlinear partial differential equations. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Arif, M.; Kumam, P. Application of Laplace-Adomian Decomposition Method for the Analytical Solution of Third-Order Dispersive Fractional Partial Differential Equations. Entropy 2019, 21, 335. [Google Scholar] [CrossRef]
- Sibatov, R.; Shulezhko, V.; Svetukhin, V. Fractional Derivative Phenomenology of Percolative Phonon-Assisted Hopping in Two-Dimensional Disordered Systems. Entropy 2017, 19, 463. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, Y.; Li, S. Exact Solutions to the Fractional Differential Equations with Mixed Partial Derivatives. Axioms 2018, 7, 10. [Google Scholar] [CrossRef]
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entropy 2012, 14, 701–716. [Google Scholar] [CrossRef]
- Cuahutenango-Barro, B.; Taneco-Hernández, M.A.; Gómez-Aguilar, J.F. On the solutions of fractional-time wave equation with memory effect involving operators with regular kernel. Chaos Solitons Fractals 2018, 115, 283–299. [Google Scholar] [CrossRef]
- Gómez-Gardeñes, J.; Latora, V. Entropy rate of diffusion processes on complex networks. Phys. Rev. 2008, 78, 065102. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.M.; Tenreiro Machado, J.A. Entropy Analysis of Soccer Dynamics. Entropy 2019, 21, 187. [Google Scholar] [CrossRef]
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Syam, M.; Al-Refai, M. Solving fractional diffusion equation via the collocation method based on fractional legendre functions. Comput. Methods Phys. 2014, 2014, 381074. [Google Scholar] [CrossRef]
- Lenzi, E.; dos Santos, M.; Michels, F.; Mendes, R.; Evangelista, L. Solutions of some nonlinear diffusion equations and generalized entropy framework. Entropy 2013, 15, 3931–3940. [Google Scholar] [CrossRef]
- Prehl, J.; Boldt, F.; Hoffmann, K.; Essex, C. Symmetric fractional diffusion and entropy production. Entropy 2016, 18, 275. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M. A finite difference/finite element technique with error estimate for space fractional tempered diffusion-wave equation. Comput. Math. Appl. 2018, 75, 2903–2914. [Google Scholar] [CrossRef]
- Lei, S.L.; Huang, Y.C. Fast algorithms for high-order numerical methods for space-fractional diffusion equations. Int. J. Comput. Math. 2017, 94, 1062–1078. [Google Scholar] [CrossRef]
- Sepahvandzadeh, A.; Ghazanfari, B.; Asadian, N. Numerical Solution of Stochastic Generalized Fractional Diffusion Equation by Finite Difference Method. Math. Comput. Appl. 2018, 23, 53. [Google Scholar] [CrossRef]
- Tripathi, N.; Das, S.; Ong, S.; Jafari, H.; Al Qurashi, M. Solution of higher order nonlinear time-fractional reaction diffusion equation. Entropy 2016, 18, 329. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. Analytical solutions of fractional order diffusion equations by natural transform method. Iran. J. Sci. Technol. Trans. Sci. 2016, 92, 1479–1490. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S. Numerical computation of fractional multi-dimensional diffusion equations by using a modified homotopy perturbation method. J. Assoc. Arab. Univ. Basic Appl. Sci. 2015, 17, 20–26. [Google Scholar] [CrossRef]
- Zafarghandi, F.S.; Mohammadi, M.; Babolian, E.; Javadi, S. Radial basis functions method for solving the fractional diffusion equations. Appl. Math. Comput. 2019, 342, 224–246. [Google Scholar] [CrossRef]
- Luchko, Y. Entropy production rate of a one-dimensional alpha-fractional diffusion process. Axioms 2016, 5, 6. [Google Scholar] [CrossRef]
- Wei, S.; Chen, W.; Zhang, Y.; Wei, H.; Garrard, R.M. A local radial basis function collocation method to solve the variable-order time fractional diffusion equation in a two-dimensional irregular domain. Numer. Methods Partial. Differ. Equ. 2018, 34, 1209–1223. [Google Scholar] [CrossRef]
- Das, S. Analytical solution of a fractional diffusion equation by variational iteration method. Comput. Math. Appl. 2009, 57, 483–487. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving coupled system of nonlinear PDE’s using the natural decomposition method. Int. J. Pure Appl. Math. 2014, 92, 757–776. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional Telegraph Equation and Its Solution by Natural Transform Decomposition Method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
- Abdel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedl-Rahim, H.R. Natural transform for solving fractional models. J. Appl. Math. Phys. 2015, 3, 1633. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Silambarasan, R. November. Advances in the natural transform. AIP Conf. Proc. 2012, 1493, 106–110. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Science Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus AND Fractional Differential Equations, 1st ed.; Wiley: London, UK, 1993; p. 384. [Google Scholar]
- Naghipour, A.; Manafian, J. Application of the Laplace Adomian decomposition and implicit methods for solving Burgers’ equation. TWMS J. Pure Appl. Math. 2015, 6, 68–77. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).