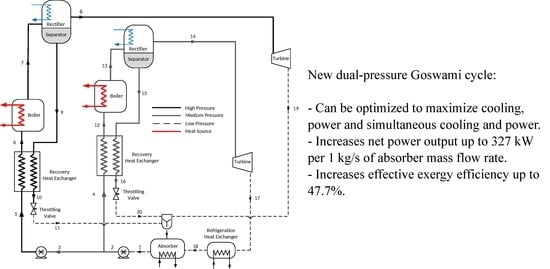
Thermal Optimization of a Dual Pressure Goswami Cycle for Low Grade Thermal Sources
Abstract
:1. Introduction
2. Materials and Methods
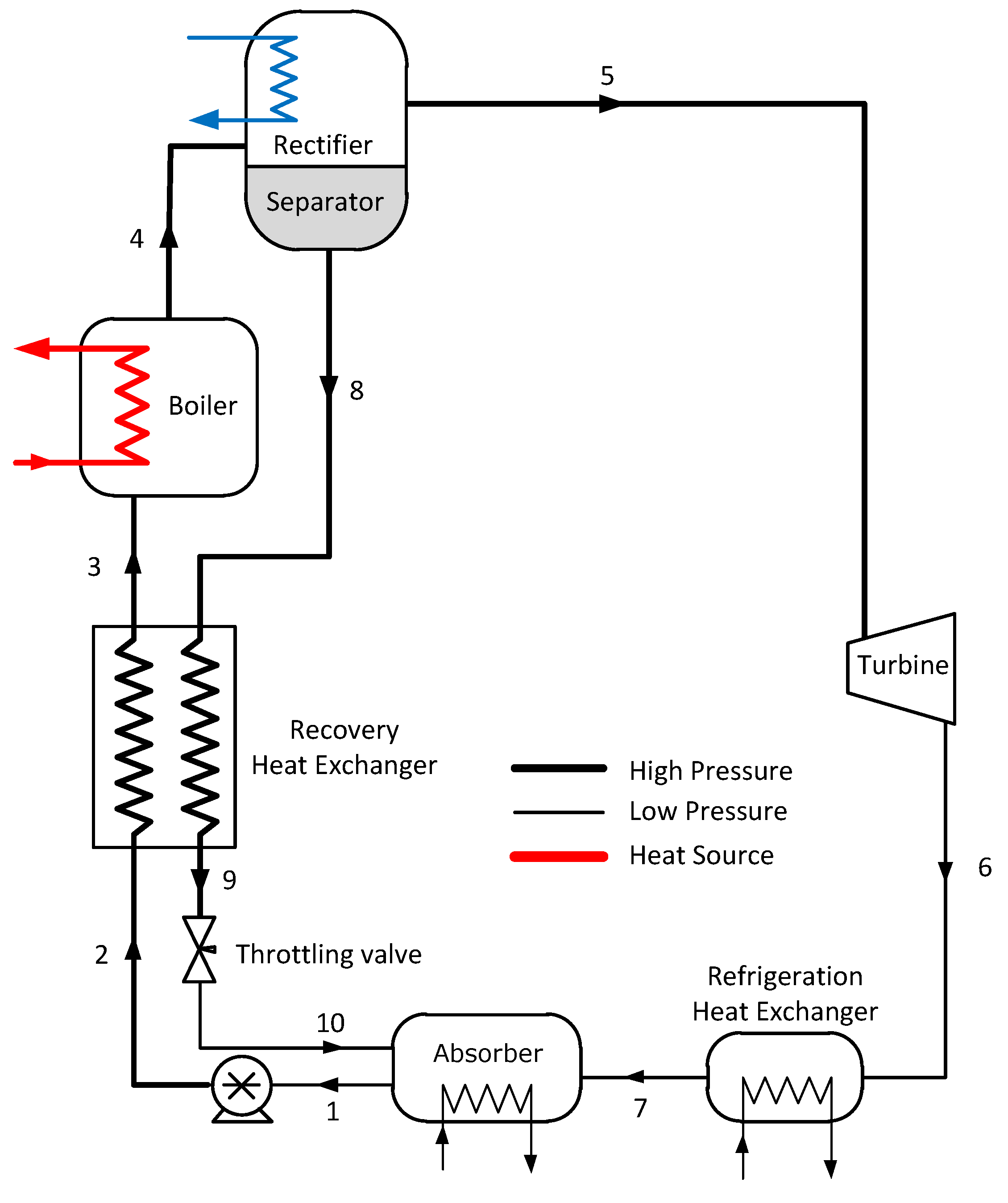
2.1. Description of the Cycle
2.2. Thermodynamic Analysis
2.2.1. Energy and Exergy Balances
2.2.2. Performance Metrics
2.3. Simulation Details
2.3.1. Parametric Study
- The system low pressure was calculated as a function of the ammonia mass fraction at the absorber outlet, , and the absorber temperature to obtain a saturated liquid leaving the absorber.
- The boiling conditions were completely specified, i.e., boiling temperature, pressure, and solution concentration were provided as inputs.
- The effectiveness value was used for the heat recovery heat exchanger, while the pinch point limitation was 10 °C for the boiler and refrigeration heat exchangers.
- Superheating was not considered in this simulation, since superheating reduces cooling output.
- Pressure drops were neglected, as Tamm et al. [11] showed that pressure losses below 5% had a negligible effect on the cycle performance. Therefore, this study suggested that all heat exchanger and piping systems must be designed to achieve pressure losses below 5%.
2.3.2. Optimization Study
3. Results and Discussion
3.1. Single-Pressure Goswami Cycle
3.2. Dual-Pressure Goswami Cycle
3.3. Pareto Optimization Results
3.4. Comparison between the Cycles
3.5. Comparison with Other Cycles
4. Conclusions
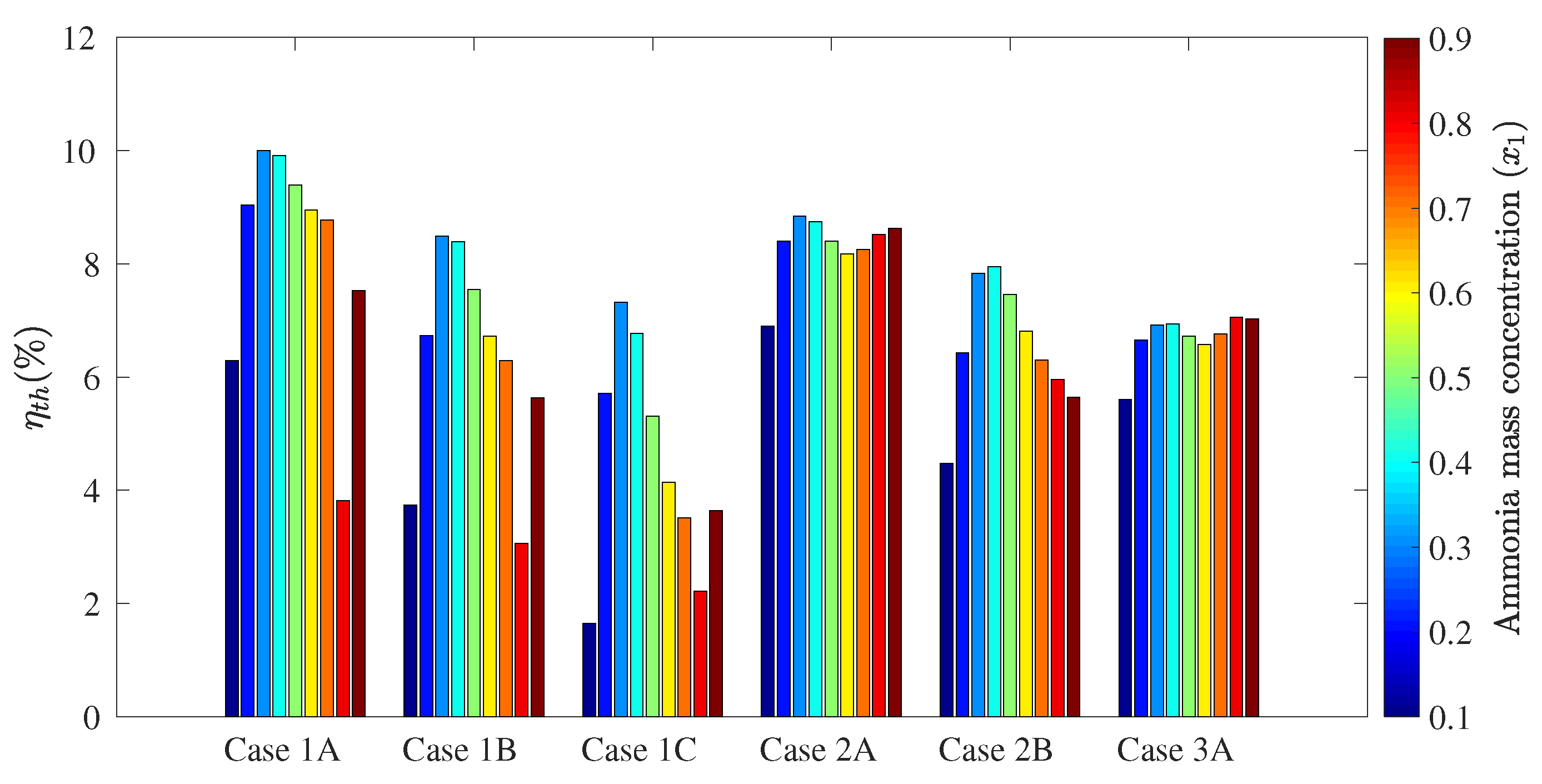
- The single-pressure configuration achieved a higher net power output by increasing the absorber ammonia mass fraction, as well as rectifier and boiler temperatures. However, higher boiler and rectifier temperatures decreased the cooling output.
- In the single-pressure configuration, simultaneous power and cooling led to higher optimum effective first law efficiencies at absorber ammonia mass fractions from 0.3–0.7 kg NH3/kg solution. Above 0.7 kg NH3/kg, effective first law efficiencies were lower as no cooling output was obtained.
- The addition of a high-pressure loop in the Goswami cycle increased net power output up to 327.8 kW, while the single-pressure configuration achieved up to 110.8 kW. However, for these values, the cooling effect was null.
- The single-pressure configuration maximized cooling output, up to 35.8 kW, while the dual-pressure configuration achieved less cooling output, up to 23.8 kW. Both configurations showed very low values of effective first law efficiencies, up to 5.9%, when cooling output was maximized.
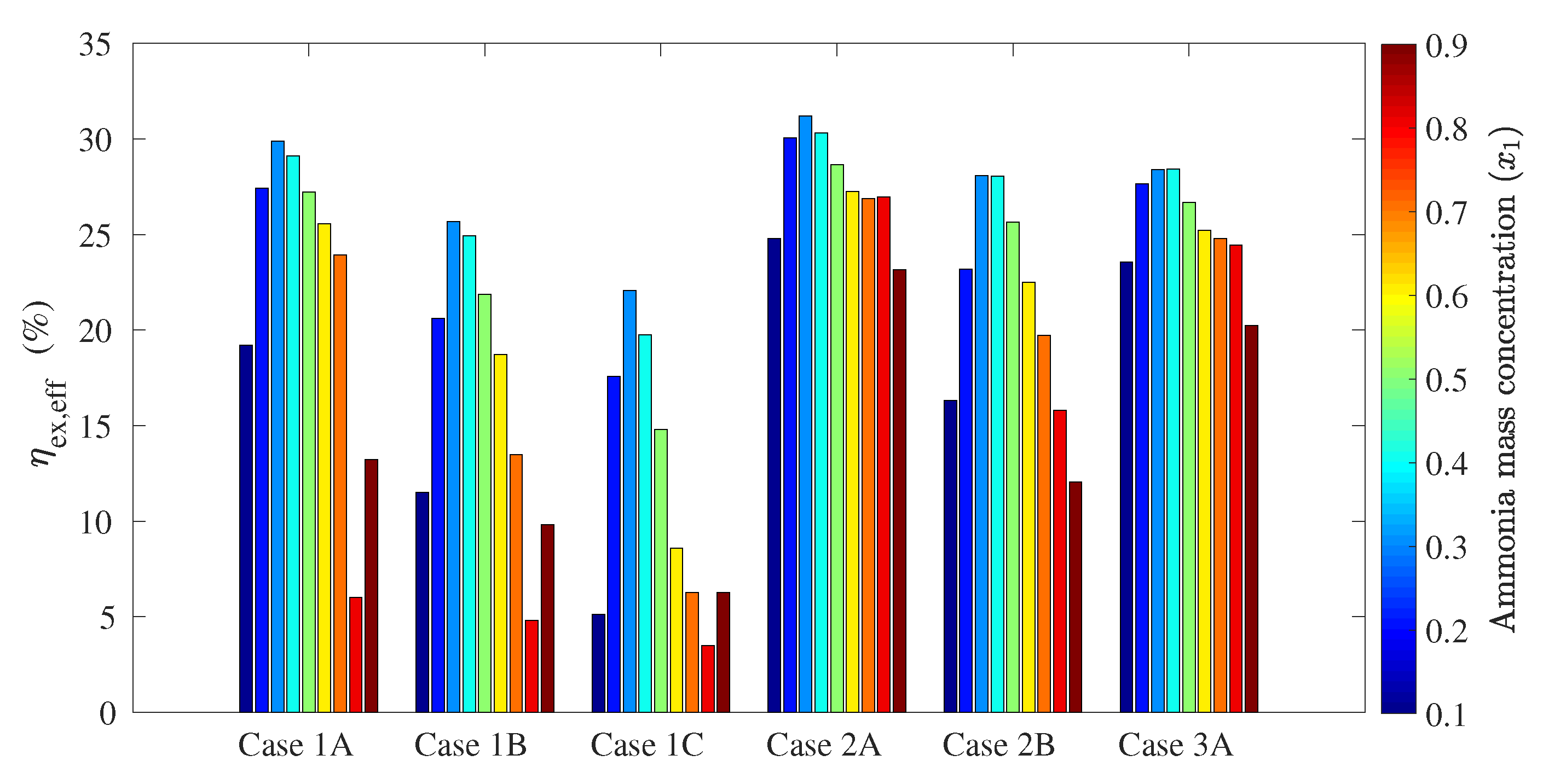
- The energy conversion process in the dual-pressure configuration increased effective exergy efficiency. The dual-pressure configuration reached up to 47.7% of effective exergy efficiency in Case 1A, and eight of the twelve tested cases showed effective exergy efficiency values above 30%, while the single-pressure configuration achieved only up to 31.2%.
- Optimization results showed that optimum cycle effective first law efficiency ranged between 9.1% and 13.7%, showing the maximum effective first law efficiency at the lowest net power (32 kW) and cooling (0.38 kW) outputs. A very close value of 13.6% for effective first law efficiency was obtained when net power was 100 kW and and cooling capacity was 0.38 kW.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Absorber ammonia mass fraction (kg NH3/kg solution) | |
| Exergy rate (kW) | |
| Exergy destruction (kW) | |
| Exergy input due to heat transfer (kW) | |
| Stream specific exergy (kJ/kg) | |
| Heat transfer input (kW) | |
| Power (kW) | |
| T | Temperature (°C or K) |
| V | Velocity (m/s) |
| m | Mass flow rate (kg/s) |
| h | Specific enthalpy (kJ/kg) |
| s | Specific entropy (kJ/kg·K) |
| g | Gravity (m/s) |
| z | Vertical position with respect to the ground (m) |
| Pressure ratio across the mid-pressure turbine () | |
| Pressure ratio across the high-pressure turbine () | |
| Subscripts | |
| cf | Chilled fluid |
| Control volume | |
| cool | Cooling |
| II | Second law |
| i | Inlet |
| e | Outlet |
| ex | Exergy |
| eff | Effective value |
| h | Heat |
| hs | Heat source |
| net | Net |
| o | Reference |
| th | First law |
| ref | Refrigeration |
| Greek symbols | |
| Efficiency | |
Appendix A. Optimum Pressure Ratio
Appendix A.1. Single-Pressure Goswami Cycle
| rp | ||||
|---|---|---|---|---|
| Optimum | Optimum | Optimum | Optimum | |
| 0.1 | 25.84 | 36.48 | 32.37 | 32.93 |
| 0.2 | 11.31 | 24.8 | 19.44 | 20.18 |
| 0.3 | 6.28 | 17.9 | 13.35 | 14.19 |
| 0.4 | 4.8 | 14.08 | 9.72 | 10.28 |
| 0.5 | 4.21 | 10.71 | 7.4 | 7.84 |
| 0.6 | 3.98 | 9.17 | 6.06 | 6.34 |
| 0.7 | 3.83 | 7.22 | 5.43 | 6.47 |
| 0.8 | 1.85 | 1.46 | 1.85 | 1.85 |
| 0.9 | 3.19 | 1.51 | 3.19 | 3.19 |
| rp | ||||
|---|---|---|---|---|
| Optimum | Optimum | Optimum | Optimum | |
| 0.1 | 28.83 | 29.76 | 33.12 | 33.49 |
| 0.2 | 13.16 | 17.78 | 20.18 | 20.92 |
| 0.3 | 7.79 | 15.54 | 14.53 | 15.03 |
| 0.4 | 5.5 | 11.69 | 10.56 | 10.99 |
| 0.5 | 4.21 | 9.16 | 7.62 | 7.95 |
| 0.6 | 3.7 | 7.47 | 5.58 | 6.24 |
| 0.7 | 3.45 | 6.18 | 4.49 | 5.24 |
| 0.8 | 1.85 | 1.01 | 1.85 | 1.85 |
| 0.9 | 2.93 | 1.01 | 3.06 | 3.09 |
| rp | ||||
|---|---|---|---|---|
| Optimum | Optimum | Optimum | Optimum | |
| 0.1 | 32 | 32.37 | 34.05 | 34.24 |
| 0.2 | 15.38 | 18.52 | 20.92 | 21.11 |
| 0.3 | 9.14 | 12.51 | 14.36 | 14.87 |
| 0.4 | 5.92 | 9.3 | 9.58 | 9.72 |
| 0.5 | 4.1 | 6.52 | 5.97 | 6.3 |
| 0.6 | 3.22 | 4.83 | 4.07 | 4.36 |
| 0.7 | 2.79 | 3.92 | 3.07 | 3.17 |
| 0.8 | 1.85 | 1.01 | 1.85 | 1.85 |
| 0.9 | 2.2 | 1.01 | 2.23 | 2.23 |
| rp | ||||
|---|---|---|---|---|
| Optimum | Optimum | Optimum | Optimum | |
| 0.1 | 10.11 | 18.7 | 15.14 | 15.66 |
| 0.2 | 4.64 | 13.49 | 9.89 | 10.4 |
| 0.3 | 3.25 | 10.23 | 7.52 | 8 |
| 0.4 | 3.26 | 8.25 | 6.01 | 6.44 |
| 0.5 | 3.1 | 6.61 | 4.96 | 5.39 |
| 0.6 | 2.99 | 5.83 | 4.38 | 4.63 |
| 0.7 | 2.95 | 5.95 | 4.14 | 4.39 |
| 0.8 | 3.11 | 5.22 | 4.13 | 4.39 |
| 0.9 | 3.27 | 4.6 | 3.91 | 4.54 |
| rp | ||||
|---|---|---|---|---|
| Optimum | Optimum | Optimum | Optimum | |
| 0.1 | 12.1 | 14.09 | 15.66 | 16.08 |
| 0.2 | 5.77 | 9.47 | 10.19 | 10.61 |
| 0.3 | 4.03 | 8.58 | 8.2 | 8.49 |
| 0.4 | 3.43 | 6.79 | 6.53 | 6.87 |
| 0.5 | 3.1 | 5.68 | 5.25 | 5.54 |
| 0.6 | 2.93 | 5.01 | 4.32 | 4.51 |
| 0.7 | 2.83 | 4.2 | 3.58 | 3.7 |
| 0.8 | 2.73 | 3.43 | 2.92 | 3.37 |
| 0.9 | 2.52 | 2.86 | 2.81 | 2.81 |
| rp | ||||
|---|---|---|---|---|
| Optimum | Optimum | Optimum | Optimum | |
| 0.1 | 5.33 | 10.76 | 8.62 | 9.02 |
| 0.2 | 3.06 | 7.82 | 6.04 | 6.37 |
| 0.3 | 2.7 | 5.96 | 4.96 | 5.27 |
| 0.4 | 2.61 | 5.19 | 4.39 | 4.62 |
| 0.5 | 2.46 | 4.37 | 3.67 | 3.92 |
| 0.6 | 2.42 | 4 | 3.32 | 3.5 |
| 0.7 | 2.46 | 4 | 3.16 | 3.38 |
| 0.8 | 2.54 | 3.43 | 3.25 | 3.34 |
| 0.9 | 2.55 | 2.88 | 2.88 | 2.88 |
Appendix A.2. Dual-Pressure Goswami Cycle
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 14.41 | 2.41 | - | - | 15.45 | 2.24 | 15.45 | 2.24 |
| 0.2 | 9.78 | 2.39 | 13.49 | 1.96 | 9.78 | 2.39 | 10.71 | 2.17 |
| 0.3 | 8.2 | 2.36 | 10.23 | 2.1 | 8.2 | 2.36 | 8.2 | 2.36 |
| 0.4 | 6.79 | 2.32 | 8.25 | 2.02 | 6.79 | 2.32 | 6.79 | 2.32 |
| 0.5 | 5.18 | 2.29 | 6.54 | 1.95 | 5.18 | 2.29 | 5.18 | 2.29 |
| 0.6 | 4.38 | 2.25 | 5.64 | 1.91 | 4.38 | 2.25 | 4.38 | 2.25 |
| 0.7 | 4.45 | 2.24 | - | - | 4.45 | 2.24 | 4.45 | 2.24 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 10.11 | 2.07 | - | - | 13.46 | 2.07 | 14.3 | 2.07 |
| 0.2 | 3.81 | 2.39 | 13.49 | 1.96 | 9.27 | 1.96 | 9.58 | 1.96 |
| 0.3 | 2.67 | 1.85 | 10.23 | 2.1 | 7.23 | 1.85 | 7.42 | 1.85 |
| 0.4 | 1.8 | 1.72 | 8.25 | 2.02 | 5.93 | 1.72 | 6.01 | 1.72 |
| 0.5 | 2.6 | 1.62 | 6.61 | 1.62 | 4.96 | 1.62 | 4.96 | 1.62 |
| 0.6 | 2.74 | 1.57 | 5.83 | 1.57 | 4.32 | 1.57 | 4.38 | 1.57 |
| 0.7 | 2.83 | 1.58 | 5.95 | 1.58 | 4.08 | 1.58 | 4.08 | 1.58 |
| 0.8 | 3.37 | 1.13 | 5.79 | 1.13 | 4.19 | 1.13 | 4.19 | 1.13 |
| 0.9 | 3.1 | 1.28 | 5.01 | 1.28 | 3.1 | 2.57 | 3.1 | 2.57 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 8.65 | 2.41 | - | - | 12.94 | 2.07 | 14.41 | 2.07 |
| 0.2 | 3.81 | 2.39 | 13.49 | 1.96 | 8.86 | 1.96 | 9.47 | 1.96 |
| 0.3 | 2.67 | 1.85 | 10.23 | 1.85 | 7.03 | 1.85 | 7.42 | 1.85 |
| 0.4 | 1.28 | 2.32 | 8.25 | 1.72 | 5.93 | 1.72 | 6.1 | 1.72 |
| 0.5 | 1.81 | 1.62 | 6.61 | 1.62 | 4.96 | 1.62 | 5.18 | 1.62 |
| 0.6 | 2.55 | 1.57 | 5.83 | 1.57 | 4.32 | 1.57 | 4.44 | 1.57 |
| 0.7 | 2.64 | 1.58 | 5.95 | 1.58 | 4.08 | 1.58 | 4.14 | 1.58 |
| 0.8 | 3.68 | 1.13 | - | - | 2.92 | 2.27 | 3.05 | 2.27 |
| 0.9 | 2.05 | 2.57 | - | - | 2.81 | 2.57 | 2.98 | 2.57 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 14.41 | 2.41 | 14.41 | 2.41 | 16.71 | 2.07 | 16.71 | 2.07 |
| 0.2 | 9.78 | 2.39 | 9.78 | 2.39 | 10.71 | 2.17 | 10.71 | 2.17 |
| 0.3 | 8.2 | 2.36 | 8.58 | 2.36 | 8.2 | 2.36 | 8.2 | 2.36 |
| 0.4 | 6.79 | 2.32 | 6.79 | 2.32 | 6.79 | 2.32 | 6.79 | 2.32 |
| 0.5 | 5.18 | 2.29 | 5.61 | 2.29 | 5.18 | 2.29 | 5.18 | 2.29 |
| 0.6 | 4.38 | 2.25 | 5.14 | 1.91 | 4.38 | 2.25 | 4.38 | 2.25 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 10.11 | 2.07 | 14.09 | 2.41 | 10.11 | 2.07 | 14.3 | 2.07 |
| 0.2 | 4.22 | 2.17 | 9.47 | 2.39 | 9.37 | 1.96 | 9.68 | 1.96 |
| 0.3 | 2.67 | 1.85 | 8.58 | 2.36 | 7.62 | 1.85 | 7.71 | 1.85 |
| 0.4 | 1.8 | 1.72 | 6.79 | 2.32 | 6.18 | 1.72 | 6.27 | 1.72 |
| 0.5 | 2.6 | 1.62 | 5.68 | 1.95 | 5.11 | 1.62 | 5.18 | 1.62 |
| 0.6 | 2.68 | 1.57 | 5.01 | 1.91 | 4.32 | 1.57 | 4.32 | 1.57 |
| 0.7 | 2.7 | 1.58 | - | - | 3.01 | 1.91 | 3.01 | 1.91 |
| 0.8 | 2.92 | 1.13 | - | - | 2.92 | 2.27 | 2.92 | 2.27 |
| 0.9 | 2.11 | 2.57 | - | - | 2.11 | 2.57 | 2.11 | 2.57 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 10.11 | 2.07 | 14.09 | 2.41 | 12.84 | 2.07 | 14.41 | 2.07 |
| 0.2 | 3.81 | 2.39 | 9.47 | 2.39 | 8.86 | 1.96 | 9.47 | 1.96 |
| 0.3 | 2.67 | 1.85 | 8.58 | 2.36 | 7.13 | 1.85 | 7.42 | 1.85 |
| 0.4 | 1.28 | 2.32 | 6.79 | 2.32 | 5.93 | 1.72 | 6.18 | 1.72 |
| 0.5 | 1.74 | 1.62 | 5.68 | 1.95 | 5.03 | 1.62 | 5.11 | 1.62 |
| 0.6 | 2.49 | 1.57 | 5.01 | 1.91 | 4.32 | 1.57 | 4.44 | 1.57 |
| 0.7 | 2.64 | 1.58 | 4.2 | 2.24 | 3.95 | 1.58 | 3.51 | 1.91 |
| 0.8 | 2.03 | 2.27 | - | - | 2.54 | 2.27 | 2.54 | 2.27 |
| 0.9 | 2 | 2.57 | - | - | 2.05 | 2.57 | 2.05 | 2.57 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 7.95 | 1.97 | - | - | 9.02 | 1.72 | 9.02 | 1.72 |
| 0.2 | 4.32 | 1.97 | 7.82 | 1.65 | 5.97 | 1.65 | 6.3 | 1.65 |
| 0.3 | 3.45 | 1.95 | 5.96 | 1.95 | 4.89 | 1.61 | 5.14 | 1.61 |
| 0.4 | 4.39 | 1.94 | 5.19 | 1.74 | 4.39 | 1.94 | 4.39 | 1.94 |
| 0.5 | 3.72 | 1.91 | 4.37 | 1.69 | 3.72 | 1.91 | 3.72 | 1.91 |
| 0.6 | 3.32 | 1.89 | 4 | 1.66 | 3.32 | 1.89 | 3.69 | 1.66 |
| 0.7 | 4.09 | 1.65 | 4.09 | 1.65 | 4.09 | 1.65 | 4.09 | 1.65 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 4.4 | 1.97 | - | - | 8.01 | 1.72 | 8.42 | 1.72 |
| 0.2 | 2.34 | 1.65 | 7.82 | 1.65 | 5.77 | 1.65 | 5.97 | 1.65 |
| 0.3 | 1.32 | 1.61 | 5.96 | 1.95 | 4.77 | 1.61 | 4.96 | 1.61 |
| 0.4 | 2.21 | 1.54 | 5.19 | 1.74 | 4.16 | 1.54 | 4.28 | 1.54 |
| 0.5 | 2.26 | 1.47 | 4.37 | 1.69 | 3.57 | 1.47 | 3.67 | 1.47 |
| 0.6 | 2.28 | 1.43 | 4 | 1.66 | 3.28 | 1.43 | 3.28 | 1.43 |
| 0.7 | 2.28 | 1.45 | 4 | 1.65 | 2.99 | 1.45 | 2.99 | 1.45 |
| 0.8 | 2.41 | 1.47 | - | - | 2.94 | 1.47 | 2.94 | 1.47 |
| 0.9 | 2.14 | 1.68 | - | - | 2.14 | 1.88 | 2.14 | 1.88 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 4.4 | 1.97 | - | - | 7.75 | 1.72 | 8.48 | 1.72 |
| 0.2 | 1.94 | 1.97 | 7.82 | 1.65 | 5.57 | 1.65 | 5.97 | 1.65 |
| 0.3 | 1.32 | 1.61 | 5.96 | 1.78 | 4.64 | 1.61 | 4.89 | 1.61 |
| 0.4 | 1.87 | 1.54 | 5.19 | 1.74 | 3.99 | 1.54 | 4.22 | 1.54 |
| 0.5 | 2.11 | 1.47 | 4.37 | 1.69 | 3.52 | 1.47 | 3.67 | 1.47 |
| 0.6 | 2.15 | 1.43 | 4 | 1.43 | 3.28 | 1.43 | 3.28 | 1.43 |
| 0.7 | 2.19 | 1.45 | 4 | 1.45 | 2.99 | 1.45 | 2.81 | 1.65 |
| 0.8 | 2.27 | 1.47 | - | - | 2.94 | 1.47 | 2.94 | 1.65 |
| 0.9 | 2.14 | 1.68 | - | - | 2.14 | 1.88 | 2.14 | 1.88 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 7.95 | 1.97 | 7.95 | 1.97 | 9.02 | 1.72 | 9.02 | 1.72 |
| 0.2 | 4.32 | 1.97 | 4.98 | 1.97 | 6.43 | 1.65 | 6.63 | 1.65 |
| 0.3 | 3.45 | 1.95 | 5.08 | 1.95 | 5.21 | 1.61 | 5.4 | 1.61 |
| 0.4 | 4.39 | 1.94 | 4.39 | 1.94 | 4.39 | 1.94 | 4.85 | 1.74 |
| 0.5 | 3.72 | 1.91 | 3.77 | 1.91 | 3.72 | 1.91 | 3.72 | 1.91 |
| 0.6 | 3.23 | 1.89 | 3.32 | 1.89 | 3.23 | 1.89 | 3.23 | 1.89 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 4.73 | 1.85 | 7.41 | 1.97 | 8.15 | 1.72 | 8.48 | 1.72 |
| 0.2 | 2.34 | 1.65 | 4.98 | 1.97 | 5.97 | 1.65 | 6.17 | 1.65 |
| 0.3 | 1.32 | 1.61 | 5.08 | 1.95 | 4.96 | 1.61 | 5.08 | 1.61 |
| 0.4 | 2.21 | 1.54 | 4.22 | 1.94 | 4.22 | 1.54 | 4.33 | 1.54 |
| 0.5 | 2.26 | 1.47 | 3.77 | 1.91 | 3.62 | 1.47 | 3.72 | 1.47 |
| 0.6 | 2.28 | 1.43 | 3.32 | 1.89 | 3.14 | 1.43 | 3.19 | 1.43 |
| 0.7 | 1.97 | 1.65 | 2.63 | 1.85 | 2.63 | 1.45 | 2.63 | 1.45 |
| 0.8 | 1.69 | 1.83 | - | - | 1.69 | 1.83 | 1.69 | 1.83 |
| 0.9 | 1.48 | 1.88 | - | - | 1.48 | 1.88 | 1.48 | 1.88 |
| Optimum | Optimum | Optimum | Optimum | |||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 4.73 | 1.85 | 7.41 | 1.97 | 7.75 | 1.72 | 8.48 | 1.72 |
| 0.2 | 1.94 | 1.97 | 4.98 | 1.97 | 5.57 | 1.65 | 5.97 | 1.65 |
| 0.3 | 1.07 | 1.95 | 5.08 | 1.95 | 4.71 | 1.61 | 4.96 | 1.61 |
| 0.4 | 1.87 | 1.54 | 4.22 | 1.94 | 4.05 | 1.54 | 4.22 | 1.54 |
| 0.5 | 2.11 | 1.47 | 3.77 | 1.91 | 3.52 | 1.47 | 3.67 | 1.47 |
| 0.6 | 2.24 | 1.43 | 3.32 | 1.89 | 3.14 | 1.43 | 3.23 | 1.43 |
| 0.7 | 1.92 | 1.65 | 2.63 | 1.85 | 2.59 | 1.65 | 2.63 | 1.65 |
| 0.8 | 1.74 | 1.83 | - | - | 1.74 | 1.83 | 1.74 | 1.83 |
| 0.9 | 1.4 | 1.88 | - | - | 1.4 | 1.88 | 1.4 | 1.88 |
Appendix B. Pareto Optimization Data
| (°C) | (°C) | (°C) | (°C) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 149.84 | 114.24 | 140.78 | 65.93 | 7.13 | 1.75 | 0.2 | 0.55 | 57.76 | 9.1 | 1.84 |
| 149.84 | 114.24 | 140.78 | 65.93 | 7.13 | 1.75 | 0.2 | 0.62 | 62.57 | 9.33 | 1.57 |
| 149.86 | 117.03 | 148.18 | 70 | 5.83 | 1.93 | 0.2 | 0.62 | 101.07 | 10.22 | 0.8 |
| 149.84 | 117.03 | 148.18 | 70 | 5.83 | 1.93 | 0.2 | 0.7 | 111.59 | 10.79 | 0.63 |
| 133.56 | 110.67 | 138.86 | 75.48 | 10.89 | 1.5 | 0.1 | 0.45 | 56.46 | 11.7 | 1.44 |
| 149.84 | 116.3 | 148.18 | 75.33 | 8.65 | 1.57 | 0.2 | 0.48 | 56.97 | 11.82 | 1.77 |
| 149.86 | 116.3 | 148.18 | 73.16 | 8.21 | 1.5 | 0.2 | 0.61 | 81.89 | 11.99 | 1.49 |
| 149.84 | 116.51 | 148.18 | 73.16 | 8.21 | 1.5 | 0.2 | 0.7 | 91.96 | 12.33 | 1.14 |
| 149.86 | 114.24 | 148.18 | 65.93 | 7.18 | 1.58 | 0.28 | 0.62 | 52.88 | 12.54 | 3.03 |
| 149.84 | 116.3 | 148.18 | 75.33 | 8.65 | 1.5 | 0.2 | 0.67 | 79.62 | 12.56 | 1.14 |
| 149.84 | 116.51 | 148.18 | 66.17 | 9.46 | 1.5 | 0.2 | 0.62 | 61.54 | 12.7 | 1.34 |
| 149.86 | 116.3 | 148.18 | 66.17 | 9.46 | 1.5 | 0.2 | 0.62 | 61.5 | 12.71 | 1.32 |
| 149.86 | 116.3 | 148.18 | 65.93 | 9.46 | 1.5 | 0.2 | 0.62 | 61.49 | 12.71 | 1.34 |
| 149.86 | 116.3 | 148.18 | 66.17 | 9.46 | 1.57 | 0.2 | 0.62 | 56.13 | 12.75 | 1.32 |
| 149.84 | 116.51 | 148.18 | 65.94 | 9.46 | 1.65 | 0.22 | 0.62 | 43.61 | 12.82 | 1.62 |
| 149.86 | 114.24 | 148.18 | 65.93 | 9.46 | 1.57 | 0.2 | 0.62 | 55.28 | 12.91 | 1.17 |
| 149.86 | 116.3 | 148.18 | 66.17 | 9.46 | 1.5 | 0.2 | 0.67 | 65.56 | 12.92 | 1.15 |
| 149.86 | 116.3 | 148.18 | 65.93 | 9.46 | 1.5 | 0.2 | 0.67 | 65.55 | 12.92 | 1.17 |
| 149.86 | 116.3 | 148.18 | 66.17 | 9.46 | 1.57 | 0.2 | 0.67 | 59.75 | 12.98 | 1.15 |
| 149.84 | 116.3 | 148.18 | 66.17 | 9.46 | 1.57 | 0.2 | 0.67 | 59.73 | 12.98 | 1.15 |
| 149.86 | 114.24 | 148.18 | 75.33 | 9.46 | 1.57 | 0.2 | 0.62 | 56.02 | 13.01 | 0.96 |
| 149.86 | 116.3 | 148.18 | 79.45 | 9.46 | 1.5 | 0.2 | 0.7 | 68.98 | 13.14 | 0.8 |
| 149.84 | 116.3 | 148.18 | 66.17 | 15.43 | 1.5 | 0.1 | 0.62 | 100.76 | 13.38 | 0.69 |
| 149.86 | 114.24 | 148.18 | 79.45 | 15.43 | 1.5 | 0.1 | 0.55 | 89.03 | 13.4 | 0.45 |
| 149.86 | 114.24 | 148.18 | 79.45 | 15.43 | 1.5 | 0.1 | 0.55 | 90.02 | 13.42 | 0.45 |
| 133.56 | 101.06 | 138.86 | 75.48 | 10.89 | 1.5 | 0.1 | 0.45 | 50.84 | 13.47 | 0.24 |
| 149.86 | 114.24 | 148.18 | 79.45 | 15.43 | 1.5 | 0.1 | 0.62 | 100.34 | 13.54 | 0.38 |
| 149.84 | 114.24 | 148.18 | 79.45 | 15.43 | 1.5 | 0.1 | 0.62 | 100.31 | 13.56 | 0.38 |
| 149.84 | 114.24 | 148.18 | 79.45 | 15.43 | 1.97 | 0.1 | 0.62 | 32.01 | 13.71 | 0.38 |
References
- Sagastume Gutiérrez, A.; Cabello Eras, J.; Sousa Santos, V.; Hernández, H.; Hens, L.; Vandecasteele, C. Electricity management in the production of lead-acid batteries: The industrial case of a production plant in Colombia. J. Clean. Prod. 2018, 198, 1443–1458. [Google Scholar] [CrossRef]
- Rosen, M.; Bulucea, C.A. Using Exergy to Understand and Improve the Efficiency of Electrical Power Technologies. Entropy 2009, 11, 820–835. [Google Scholar] [CrossRef]
- Maraver, D.; Quoilin, S.; Royo, J. Optimization of Biomass-Fuelled Combined Cooling, Heating and Power (CCHP) Systems Integrated with Subcritical or Transcritical Organic Rankine Cycles (ORCs). Entropy 2014, 16, 2433–2453. [Google Scholar] [CrossRef] [Green Version]
- Fontalvo, A.; Solano, J.; Pedraza, C.; Bula, A.; González Quiroga, A.; Vásquez Padilla, R. Energy, Exergy and Economic Evaluation Comparison of Small-Scale Single and Dual Pressure Organic Rankine Cycles Integrated with Low-Grade Heat Sources. Entropy 2017, 19, 476. [Google Scholar] [CrossRef]
- Valencia, G.; Fontalvo, A.; Cárdenas, Y.; Duarte, J.; Isaza, C. Energy and Exergy Analysis of Different Exhaust Waste Heat Recovery Systems for Natural Gas Engine Based on ORC. Energies 2019, 12, 2378. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Xue, X.; Wang, G.; Mei, S. Thermodynamic Analysis of a Hybrid Power System Combining Kalina Cycle with Liquid Air Energy Storage. Entropy 2019, 21, 220. [Google Scholar] [CrossRef]
- Xu, F.; Goswami, D.Y.; Bhagwat, S.S. A combined power/cooling cycle. Energy 2000, 25, 233–246. [Google Scholar] [CrossRef]
- Wu, D.; Wang, R. Combined cooling, heating and power: A review. Progr. Energy Combust. Sci. 2006, 32, 459–495. [Google Scholar] [CrossRef]
- Martin, C.; Goswami, D.Y. Effectiveness of cooling production with a combined power and cooling thermodynamic cycle. Appl. Therm. Eng. 2006, 26, 576–582. [Google Scholar] [CrossRef]
- Hasan, A.A.; Goswami, D.Y.; Vijayaraghavan, S. First and second law analysis of a new power and refrigeration thermodynamic cycle using a solar heat source. Sol. Energy 2002, 73, 385–393. [Google Scholar] [CrossRef]
- Tamm, G.; Goswami, D.Y.; Lu, S.; Hasan, A.A. Theoretical and experimental investigation of an ammonia–water power and refrigeration thermodynamic cycle. Sol. Energy 2004, 76, 217–228. [Google Scholar] [CrossRef]
- Vijayaraghavan, S.; Goswami, D.Y. On Evaluating Efficiency of a Combined Power and Cooling Cycle. J. Energy Resour. Technol. 2003, 125, 221–227. [Google Scholar] [CrossRef]
- Padilla, R.V.; Demirkaya, G.; Goswami, D.Y.; Stefanakos, E.; Rahman, M.M. Analysis of power and cooling cogeneration using ammonia-water mixture. Energy 2010, 35, 4649–4657. [Google Scholar] [CrossRef]
- Pouraghaie, M.; Atashkari, K.; Besarati, S.; Nariman-zadeh, N. Thermodynamic performance optimization of a combined power/cooling cycle. Energy Convers. Manag. 2010, 51, 204–211. [Google Scholar] [CrossRef]
- Demirkaya, G.; Besarati, S.M.; Padilla, R.V.; Archibold, A.R.; Rahman, M.M.; Goswami, D.Y.; Stefanakos, E.L. Multi-objetive optimization of a combined power and cooling cycle for low-grade and mid-grade heat sources. J. Energy Resour. Technol. 2012, 134, 032002. [Google Scholar] [CrossRef]
- Fontalvo, A.; Pinzon, H.; Duarte, J.; Bula, A.; Quiroga, A.G.; Padilla, R.V. Exergy analysis of a combined power and cooling cycle. Appl. Therm. Eng. 2013, 60, 164–171. [Google Scholar] [CrossRef]
- Demirkaya, G.; Padilla, R.V.; Goswami, D.Y.; Stefanakos, E.; Rahman, M. Analysis of a combined power and cooling cycle for low-grade heat sources. Int. J. Energy Res. 2011, 35, 1145–1157. [Google Scholar] [CrossRef]
- Demirkaya, G.; Padilla, R.V.; Fontalvo, A.; Lake, M.; Lim, Y.Y. Thermal and Exergetic Analysis of the Goswami Cycle Integrated with Mid-Grade Heat Sources. Entropy 2017, 19, 416. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Xu, F.; Goswami, D.Y. Thermodynamic properties of ammonia–water mixtures for power-cycle applications. Energy 1999, 24, 525–536. [Google Scholar] [CrossRef]
- Tillner-Roth, R.; Friend, D. A Helmholtz free energy formulation of the thermodynamic properties of the mixture water + ammonia. J. Phys. Chem. Ref. Data 1998, 27, 63. [Google Scholar] [CrossRef]
- Demirkaya, G.; Padilla, R.V.; Fontalvo, A.; Bula, A.; Goswami, D.Y. Experimental and theoretical analysis of the Goswami cycle operating at low temperature heat sources. J. Energy Resour. Technol. 2018, 140, 072005. [Google Scholar] [CrossRef]
- Ogriseck, S. Integration of Kalina cycle in a combined heat and power plant, a case study. Appl. Therm. Eng. 2009, 29, 2843–2848. [Google Scholar] [CrossRef] [Green Version]
- Ayou, D.S.; Joan Carles, B.; Alberto, C. Combined absorption power and refrigeration cycles using low- and mid-grade heat sources. Sci. Technol. Built Environ. 2015, 21, 934–943. [Google Scholar] [CrossRef]
- Astolfi, M.; Romano, M.; Bombarda, P.; Macchi, E. Binary ORC (organic Rankine cycles) power plants for the exploitation of medium–low temperature geothermal sources—Part A: Thermodynamic optimization. Energy 2014, 66, 423–434. [Google Scholar] [CrossRef]
- Sun, L.; Han, W.; Jing, X.; Zheng, D.; Jin, H. A power and cooling cogeneration system using mid/low-temperature heat source. Appl. Energy 2013, 112, 886–897. [Google Scholar] [CrossRef]
- Wang, J.; Dai, Y.; Zhang, T.; Ma, S. Parametric analysis for a new combined power and ejector–absorption refrigeration cycle. Energy 2009, 34, 1587–1593. [Google Scholar] [CrossRef]
- Erickson, D.C.; Anand, G.; Kyung, I. Heat-activated dual-function absorption cycle. ASHRAE Trans. 2004, 110, 515–524. [Google Scholar]
- Takeshita, K.; Amano, Y.; Hashizume, T. Experimental study of advanced cogeneration system with ammonia–water mixture cycles at bottoming. Energy 2005, 30, 247–260. [Google Scholar] [CrossRef]
- Jawahar, C.P.; Saravanan, R.; Bruno, J.C.; Coronas, A. Simulation studies on gax based Kalina cycle for both power and cooling applications. Appl. Therm. Eng. 2013, 50, 1522–1529. [Google Scholar] [CrossRef]
- Hua, J.; Chen, Y.; Wang, Y.; Roskilly, A.P. Thermodynamic analysis of ammonia–water power/chilling cogeneration cycle with low-grade waste heat. Appl. Therm. Eng. 2014, 64, 483–490. [Google Scholar] [CrossRef]









| Case | (°C) | (°C) | (kg NH3/kg sol) |
|---|---|---|---|
| 1A | 150 | 120 | 0.1–0.9 |
| 1B | 150 | 100 | 0.1–0.9 |
| 1C | 150 | 80 | 0.1–0.9 |
| 2A | 120 | 100 | 0.1–0.9 |
| 2B | 120 | 80 | 0.1–0.9 |
| 3A | 100 | 80 | 0.1–0.9 |
| Parameter | Value | Units |
|---|---|---|
| Pinch point | 10 | °C |
| Reference temperature | 25 | °C |
| Reference pressure | 1 | bar |
| Absorber temperature | 35 | °C |
| Second law efficiency of refrigeration [12] | 30% | |
| Recovery heat exchanger effectiveness | 85% | |
| Isentropic turbine efficiency | 85% | |
| Minimum turbine exit vapor quality | 90% | |
| Isentropic pump efficiency | 85% |
| Case | (°C) | (°C) | (°C) | (°C) | (kg NH3/kg sol) | |
|---|---|---|---|---|---|---|
| 1AA | 150 | 120 | 150 | 100 | 0.1 | 0.1–0.9 |
| 1AB | 150 | 120 | 150 | 100 | 0.4 | 0.1–0.9 |
| 1AC | 150 | 120 | 150 | 100 | 0.8 | 0.1–0.9 |
| 1BA | 150 | 120 | 150 | 80 | 0.1 | 0.1–0.9 |
| 1BB | 150 | 120 | 150 | 80 | 0.4 | 0.1–0.9 |
| 1BC | 150 | 120 | 150 | 80 | 0.8 | 0.1–0.9 |
| 2AA | 120 | 100 | 120 | 80 | 0.1 | 0.1–0.9 |
| 2AB | 120 | 100 | 120 | 80 | 0.4 | 0.1–0.9 |
| 2AC | 120 | 100 | 120 | 80 | 0.8 | 0.1–0.9 |
| 2BA | 120 | 100 | 120 | 60 | 0.1 | 0.1–0.9 |
| 2BB | 120 | 100 | 120 | 60 | 0.4 | 0.1–0.9 |
| 2BC | 120 | 100 | 120 | 60 | 0.8 | 0.1–0.9 |
| (°C) | (°C) | (°C) | (°C) | |||||
|---|---|---|---|---|---|---|---|---|
| Lower limit | 0.1 | 0.1 | 1.2 | 1.5 | 80 | 60 | 80 | 50 |
| Upper limit | 0.9 | 0.8 | 2.0 | 4.0 | 150 | 120 | 150 | 80 |
| Cycle Type | Ref. | Boiler (°C) | Condenser (°C) | |||
|---|---|---|---|---|---|---|
| GAX+ Absorption Ref. | [28] | 155 | 28 | 30 | 11.9 | - |
| Rankine + Ejector Ref. | [27] | 212 | 25 | 39 | 20.9 | 35.8 |
| [26] | 350 | 40.3 | 23.7 | 18.6 | 42.0 | |
| Kalina + Absorption Ref. | [29] | 159 | 27 | 31 | 26 | - |
| [30] | 160 | 25 | 32 | 11.1 | - | |
| [31] | 200 | 25 | 37 | 16.4 | 48.3 | |
| SSAPRC-S | [24] | 220 | 30 | 48 | 14.6 | - |
| TSAPRC-S | [24] | 220 | 30 | 39 | 16.8 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán, G.; De Los Reyes, L.; Noriega, E.; Ramírez, H.; Bula, A.; Fontalvo, A. Thermal Optimization of a Dual Pressure Goswami Cycle for Low Grade Thermal Sources. Entropy 2019, 21, 711. https://doi.org/10.3390/e21070711
Guzmán G, De Los Reyes L, Noriega E, Ramírez H, Bula A, Fontalvo A. Thermal Optimization of a Dual Pressure Goswami Cycle for Low Grade Thermal Sources. Entropy. 2019; 21(7):711. https://doi.org/10.3390/e21070711
Chicago/Turabian StyleGuzmán, Gustavo, Lucía De Los Reyes, Eliana Noriega, Hermes Ramírez, Antonio Bula, and Armando Fontalvo. 2019. "Thermal Optimization of a Dual Pressure Goswami Cycle for Low Grade Thermal Sources" Entropy 21, no. 7: 711. https://doi.org/10.3390/e21070711
APA StyleGuzmán, G., De Los Reyes, L., Noriega, E., Ramírez, H., Bula, A., & Fontalvo, A. (2019). Thermal Optimization of a Dual Pressure Goswami Cycle for Low Grade Thermal Sources. Entropy, 21(7), 711. https://doi.org/10.3390/e21070711