Efficiency Bounds for Minimally Nonlinear Irreversible Heat Engines with Broken Time-Reversal Symmetry
Abstract
:1. Introduction
2. Minimally Nonlinear Irreversible Heat Engine with Broken Time-Reversal Symmetry
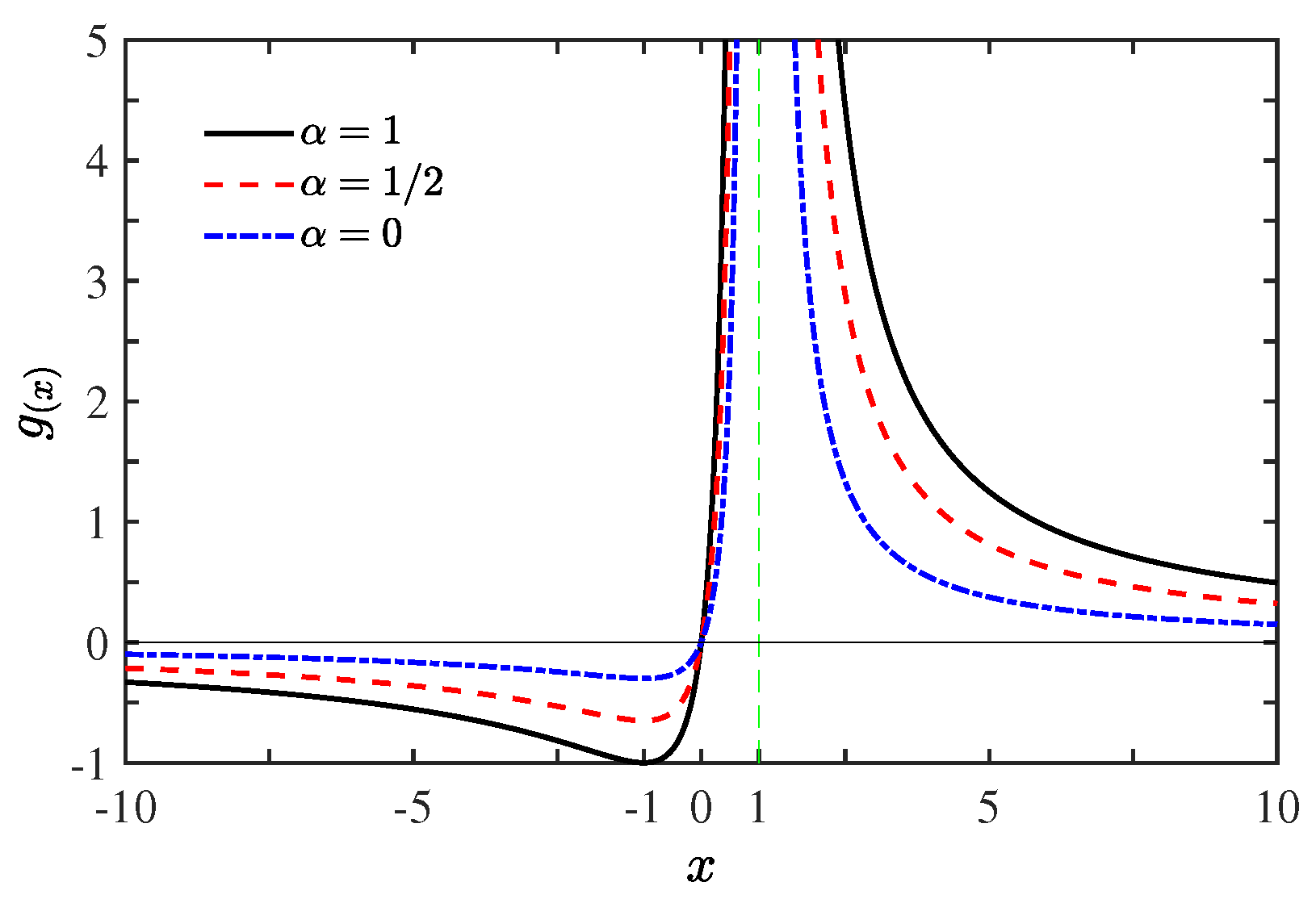
3. Maximum Efficiency
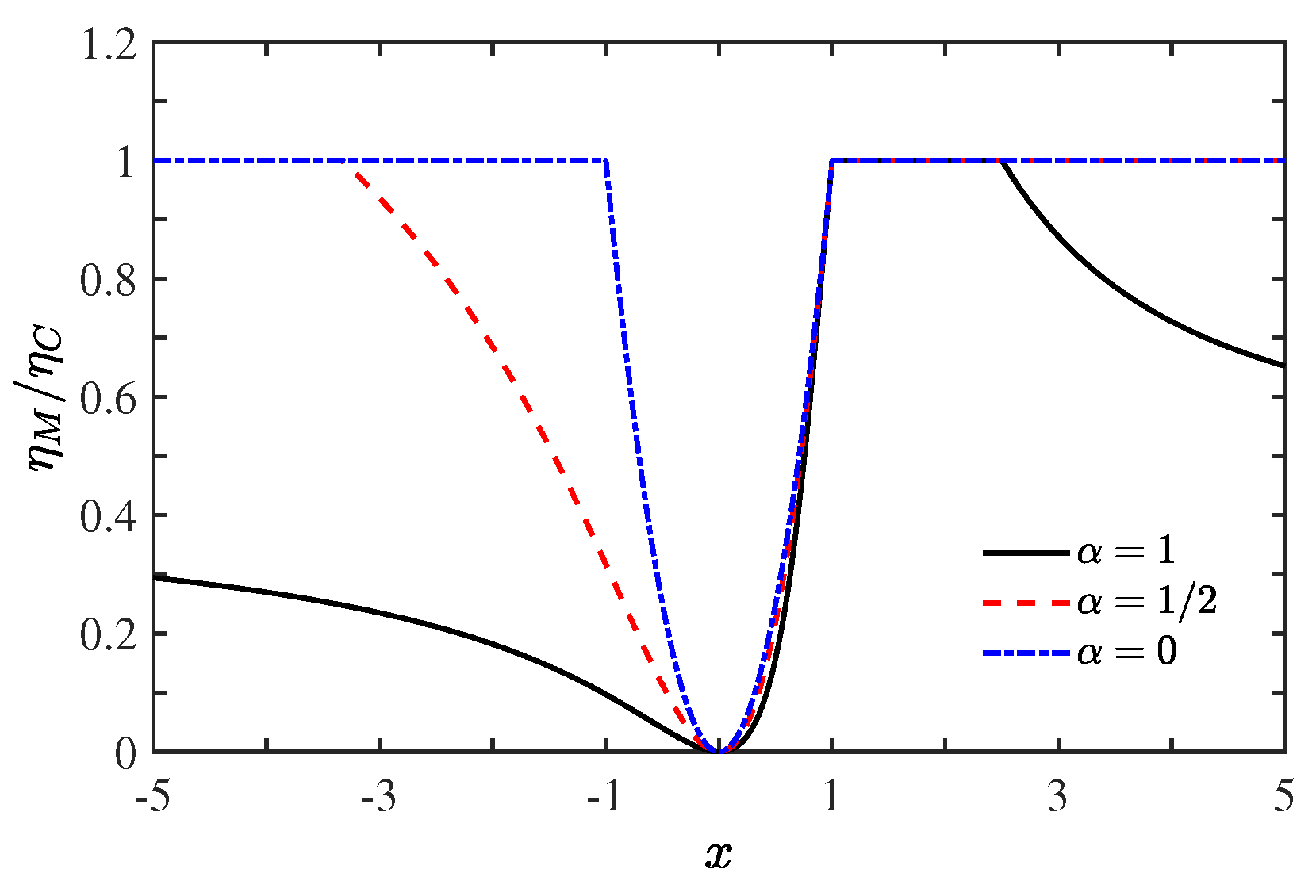
4. Efficiency at Maximum Power
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Symbol | Description |
| Temperature of the hot heat reservoir | |
| Temperature of the cold heat reservoir | |
| Heat current extracted from the hot reservoir | |
| Heat current injected into the cold reservoir | |
| Entropy production rate | |
| with | Thermodynamic fluxes |
| with | Thermodynamic forces |
| Efficiency | |
| Carnot efficiency | |
| Maximum efficiency | |
| The upper bound of efficiency at maximum power | |
| P | Power output |
| Maximum power | |
| Power at maximum efficiency | |
| Dissipation ratio | |
| External field | |
| x | Asymmetry parameter |
References
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, J.; Sun, F. Ecological optimization for generalized irreversible Carnot engines. Appl. Energy 2004, 77, 327–338. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Quantum four-stroke heat engine: Thermodynamic observables in a model with intrinsic friction. Phys. Rev. E 2003, 68, 016101. [Google Scholar] [CrossRef] [PubMed]
- Rezek, Y.; Kosloff, R. Irreversible performance of a quantum harmonic heat engine. New J. Phys. 2006, 8, 83. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Efficiency of molecular motors at maximum power. EPL (Europhys. Lett.) 2008, 83, 30005. [Google Scholar] [CrossRef] [Green Version]
- Esposito, M.; Kawai, R.; Lindenberg, K. Quantum-dot Carnot engine at maximum power. Phys. Rev. E 2010, 81, 041106. [Google Scholar] [CrossRef] [Green Version]
- Apertet, Y.; Ouerdane, H.; Goupil, C. Efficiency at maximum power of thermally coupled heat engines. Phys. Rev. E 2012, 85, 041144. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Wang, Y.; Chen, J. General performance characteristics and parametric optimum bounds of irreversible chemical engines. J. Appl. Phys. 2012, 112, 103504. [Google Scholar] [CrossRef]
- Abah, O.; Rossnagel, J.; Jacob, G. Single-ion heat engine at maximum power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Wang, J.; Wang, Y. Universal efficiency bounds of weak-dissipative thermodynamic cycles at the maximum power output. Phys. Rev. E 2013, 87, 012133. [Google Scholar] [CrossRef] [PubMed]
- Sheng, S.; Tu, Z.C. Weighted reciprocal of temperature, weighted thermal flux, and their applications in finite-time thermodynamics. Phys. Rev. E 2014, 89, 012129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, R.; Liu, W. Unified trade-off optimization for general heat devices with nonisothermal processes. Phys. Rev. E 2015, 91, 042127. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; He, J.; Wang, J. Efficiency at maximum power for an Otto engine with ideal feedback. J. Appl. Phys. 2016, 120, 154303. [Google Scholar] [CrossRef]
- Ryabov, A.; Holubec, V. Maximum efficiency of steady-state heat engines at arbitrary power. Phys. Rev. E 2016, 93, 050101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, R.; Liu, W. Efficiency and its bounds of minimally nonlinear irreversible heat engines at arbitrary power. Phys. Rev. E 2016, 94, 052114. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Liu, W.; Li, Q. Optimal performance at arbitrary power of minimally nonlinear irreversible thermoelectric generators with broken time-reversal symmetry. Phys. Lett. A 2018, 382, 20–26. [Google Scholar] [CrossRef]
- Pietzonka, P.; Seifert, U. Universal trade-off between power, efficiency, and constancy in steady-state heat engines. Phys. Rev. Lett. 2018, 120, 190602. [Google Scholar] [CrossRef]
- Van den Broeck, C. Thermodynamic efficiency at maximum power. Phys. Rev. Lett. 2005, 95, 190602. [Google Scholar] [CrossRef]
- Brandner, K.; Saito, K.; Seifert, U. Thermodynamics of micro-and nano-systems driven by periodic temperature variations. Phys. Rev. X 2015, 5, 031019. [Google Scholar] [CrossRef]
- Van den Broeck, C.; Esposito, M. Ensemble and trajectory thermodynamics: A brief introduction. Phys. A Stat. Mech. Appl. 2015, 418, 6–16. [Google Scholar] [CrossRef] [Green Version]
- Esposito, M.; Kawai, R.; Lindenberg, K. Efficiency at maximum power of low-dissipation Carnot engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ye, Z.; Lai, Y. Efficiency at maximum power of a quantum heat engine based on two coupled oscillators. Phys. Rev. E 2015, 91, 062134. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; He, J.; Ma, Y. Efficiency at maximum power of a quantum Otto cycle within finite-time or irreversible thermodynamics. Phys. Rev. E 2014, 90, 062134. [Google Scholar] [CrossRef] [Green Version]
- Izumida, Y.; Okuda, K. Efficiency at maximum power of minimally nonlinear irreversible heat engines. EPL (Europhys. Lett.) 2012, 97, 10004. [Google Scholar] [CrossRef]
- Gonzalez-Ayala, J.; Roco, J.M.M. From maximum power to a trade-off optimization of low-dissipation heat engines: Influence of control parameters and the role of entropy generation. Phys. Rev. E 2017, 95, 022131. [Google Scholar] [CrossRef]
- Benenti, G.; Saito, K.; Casati, G. Thermodynamic bounds on efficiency for systems with broken time-reversal symmetry. Phys. Rev. Lett. 2011, 106, 230602. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Hovhannisyan, K.V.; Melkikh, A.V. Carnot cycle at finite power: Attainability of maximal efficiency. Phys. Rev. Lett. 2013, 111, 050601. [Google Scholar] [CrossRef]
- Whitney, R.S. Most efficient quantum thermoelectric at finite power output. Phys. Rev. Lett. 2014, 112, 130601. [Google Scholar] [CrossRef]
- Polettini, M.; Verley, G.; Esposito, M. Efficiency statistics at all times: Carnot limit at finite power. Phys. Rev. Lett. 2015, 114, 050601. [Google Scholar] [CrossRef] [PubMed]
- Proesmans, K.; Van den Broeck, C. Onsager coefficients in periodically driven systems. Phys. Rev. Lett. 2015, 115, 090601. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Fazio, R. The power of a critical heat engine. Nat. Commun. 2016, 7, 11895. [Google Scholar] [CrossRef] [PubMed]
- Shiraishi, N. Attainability of Carnot efficiency with autonomous engines. Phys. Rev. E 2015, 92, 050101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnson, C.V. Approaching the Carnot limit at finite power: An exact solution. arXiv 2017, arXiv:1703.06119. [Google Scholar]
- Lee, J.S.; Park, H. Carnot efficiency is reachable in an irreversible process. Sci. Rep. 2017, 7, 10725. [Google Scholar] [CrossRef] [PubMed]
- Polettini, M.; Esposito, M. Carnot efficiency at divergent power output. EPL (Europhys. Lett.) 2017, 118, 40003. [Google Scholar] [CrossRef] [Green Version]
- Brandner, K.; Seifert, U. Bound on thermoelectric power in a magnetic field within linear response. Phys. Rev. E 2015, 91, 012121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, J.H. Thermodynamic bounds and general properties of optimal efficiency and power in linear responses. Phys. Rev. E 2014, 90, 042126. [Google Scholar] [CrossRef] [Green Version]
- Bauer, M.; Brandner, K.; Seifert, U. Optimal performance of periodically driven, stochastic heat engines under limited control. Phys. Rev. E 2016, 93, 042112. [Google Scholar] [CrossRef]
- Shiraishi, N.; Saito, K.; Tasaki, H. Universal trade-off relation between power and efficiency for heat engines. Phys. Rev. Lett. 2016, 117, 190601. [Google Scholar] [CrossRef] [PubMed]
- Proesmans, K.; Cleuren, B.; Van den Broeck, C. Power-efficiency-dissipation relations in linear thermodynamics. Phys. Rev. Lett. 2016, 116, 220601. [Google Scholar] [CrossRef] [PubMed]
- Iyyappan, I.; Ponmurugan, M. General relations between the power, efficiency, and dissipation for the irreversible heat engines in the nonlinear response regime. Phys. Rev. E 2018, 97, 012141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brandner, K.; Seifert, U. Multi-terminal thermoelectric transport in a magnetic field: Bounds on Onsager coefficients and efficiency. New J. Phys. 2013, 15, 105003. [Google Scholar] [CrossRef]
- Yamamoto, K.; Entin-Wohlman, O.; Aharony, A. Efficiency bounds on thermoelectric transport in magnetic fields: The role of inelastic processes. Phys. Rev. B 2016, 94, 121402. [Google Scholar] [CrossRef] [Green Version]
- Koning, J.; Indekeu, J.O. Engines with ideal efficiency and nonzero power for sublinear transport laws. Eur. Phys. J. B 2016, 89, 248. [Google Scholar] [CrossRef]
- Sonnino, G.; Evslin, J.; Sonnino, A.; Steinbrecher, G.; Tirapegui, E. Symmetry group and group representations associated with the thermodynamic covariance principle. Phys. Rev. E 2016, 94, 042103. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Lu, J.; Wang, C. Nonlinear effects for three-terminal heat engine and refrigerator. Sci. Rep. 2018, 8, 2607. [Google Scholar] [CrossRef]
- Jiang, J.H.; Imry, Y. Enhancing thermoelectric performance using nonlinear transport effects. Phys. Rev. Appl. 2017, 7, 064001. [Google Scholar] [CrossRef]
- Sothmann, B.; Jordan, A.N. Powerful energy harvester based on resonant-tunneling quantum wells. New J. Phys. 2013, 15, 095021. [Google Scholar] [CrossRef] [Green Version]
- Izumida, Y.L.; Okuda, K. Coefficient of performance under optimized figure of merit in minimally nonlinear irreversible refrigerator. EPL (Europhys. Lett.) 2013, 101, 10005. [Google Scholar] [CrossRef]
- Holubec, V.; Ryabov, A. Diverging, but negligible power at Carnot efficiency: Theory and experiment. Phys. Rev. E 2017, 96, 062107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, J.H.; Agarwalla, B.K.; Segal, D. Efficiency statistics and bounds for systems with broken time-reversal symmetry. Phys. Rev. Lett. 2015, 115, 040601. [Google Scholar] [CrossRef] [PubMed]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Li, W.; Zhang, M.; He, J.; Wang, J. Efficiency Bounds for Minimally Nonlinear Irreversible Heat Engines with Broken Time-Reversal Symmetry. Entropy 2019, 21, 717. https://doi.org/10.3390/e21070717
Liu Q, Li W, Zhang M, He J, Wang J. Efficiency Bounds for Minimally Nonlinear Irreversible Heat Engines with Broken Time-Reversal Symmetry. Entropy. 2019; 21(7):717. https://doi.org/10.3390/e21070717
Chicago/Turabian StyleLiu, Qin, Wei Li, Min Zhang, Jizhou He, and Jianhui Wang. 2019. "Efficiency Bounds for Minimally Nonlinear Irreversible Heat Engines with Broken Time-Reversal Symmetry" Entropy 21, no. 7: 717. https://doi.org/10.3390/e21070717
APA StyleLiu, Q., Li, W., Zhang, M., He, J., & Wang, J. (2019). Efficiency Bounds for Minimally Nonlinear Irreversible Heat Engines with Broken Time-Reversal Symmetry. Entropy, 21(7), 717. https://doi.org/10.3390/e21070717



