A Novel Autonomous Perceptron Model for Pattern Classification Applications
Abstract
:1. Introduction
- The APM is designed with an optimal neural structure of only one single neuron to classify nonlinear separable datasets.
- The APM is able to construct the neural network activation operators autonomously.
- The APM is a robust classifier that is able to compete favourably with several standard classifiers and can be implemented in a limited number of iterations.
2. Background
2.1. Quantum Computation
2.2. Quantum Bit
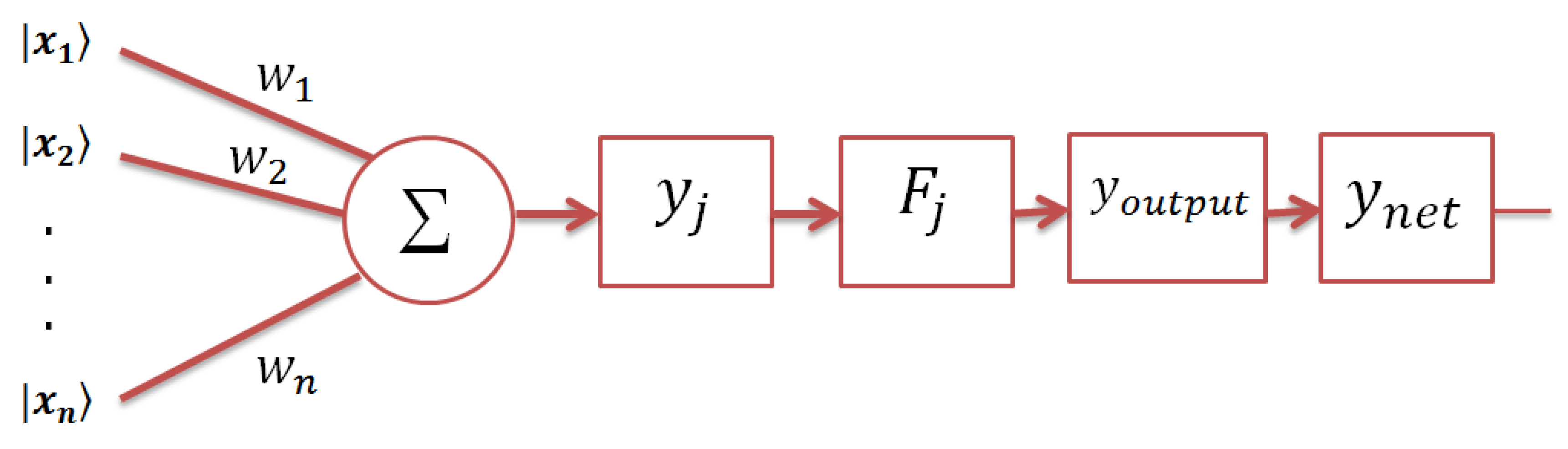
2.3. The Perceptron Model
3. Related Work
3.1. Previously Proposed Models
3.2. Limitations and Motivation
4. The Autonomous Perceptron Model
4.1. The Computational Subspace of APM
4.2. The Topological Structure of APM
4.3. The Learning Algorithm of APM
| Algorithm 1: The training algorithm of APM. |
| Step 1: Set all (identity matrix). Then, choose the initial weight operators randomly and the number of iterations (). Step 2: For k = 1 : For training patterns Calculate the weighted sum vector using Equation (4) for each pattern . End For Update the weight operators using Equation (7). End For Step 3: Compare each weighted sum vector for the patterns of each class label in the dataset with all other weighted sum vectors for other classes in the same dataset. In this case, it may be possible that any weighted sum vector for any class equals the weighted sum of any other class. If this is the case, then go to Step 4; otherwise, go to Step 5. Step 4: Re-initialize weight operators by the same way shown in Step 1, and go to Step 2. Step 5: Calculate the activation operator for each weighted sum qubit using Equation (6). |
| Algorithm 2: The testing algorithm of APM. |
| Step 1: For a test pattern do { Compute the weighted sum of the test pattern as: For End For End For Step 2: The predicted class label of the test pattern is given by the net response of the APM as given by Equation (9). |
5. The Computational Capability of APM
6. Experiments and Results
6.1. Learning a Logical Function
6.2. Classification Experiments
6.2.1. Experimental Settings
6.2.2. Experimental Results
7. Time Complexity Analysis
7.1. Comparison with Baseline Classifiers
7.2. Comparison with Multilayer Perceptron MLP using Big-O Analysis
7.2.1. Big-O Analysis for the MLP Model
7.2.2. Big-O Analysis for the APM Model
8. Results’ Discussion and Analysis
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, G. Neural Networks for Classification: A Survey. IEEE Trans. Syst. Man Cybern. Part C 2000, 30, 451–462. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Jenhani, I.; BenAmor, N.; Elouedi, Z. Decision trees as possibilistic classifiers. Int. J. Approx. Reason. 2008, 48, 748–807. [Google Scholar] [CrossRef]
- Rodionova, O.; Alexey, A.; Pomerantseva, L. Discriminant analysis is an inappropriate method of authentication. Trends Anal. Chem. TrAC 2016, 78, 17–22. [Google Scholar] [CrossRef]
- Jia, W.; Zhaob, D.; Dingd, L. An optimized RBF neural network algorithm based on partial leastsquares and genetic algorithm for classification of small sample. Appl. Soft Comput. 2016, 48, 373–384. [Google Scholar] [CrossRef]
- Berardi, V.; Patuwo, B.; Hu, M. A principled approach for building and evaluating neural network classification models. Decis. Support Syst. 2004, 38, 233–246. [Google Scholar] [CrossRef]
- Huang, Y. Advances in Artificial Neural Networks Methodological Development and Application. Algorithms 2009, 2, 973–1007. [Google Scholar] [CrossRef]
- Buckely, J.; Hayashi, Y. Fuzzy neural networks—A Survey. Fuzzy Sets Syst. 1994, 66, 1–13. [Google Scholar] [CrossRef]
- Ding, H.; Wu, J.; Li, X. Evolving neural network using hybrid genetic algorithm and simulated annealing for rainfall runoff forecasting. In Proceedings of the International Conference in Swarm Intelligence, Chongqing, China, 12–15 June 2011; pp. 444–451. [Google Scholar]
- Dunjko, V.; Briegel, H.J. Machine learning & artificial intelligence in the quantum domain: A review of recent progress. Rep. Prog. Phys. 2018, 81, 074001. [Google Scholar]
- Schuld, M.; Sinayshiy, I.; Petruccione, F. The quest for a quantum neural network. Quantum Inf. Proc. 2014, 13, 2567–2586. [Google Scholar] [CrossRef]
- Shafee, F. Neural networks with quantum gated nodes. Eng. Appl. Artif. Intel. 2007, 20, 429–437. [Google Scholar] [CrossRef]
- Zhou, R. Quantum competitive neural network. Int. Theor. Phys. 2010, 49, 110–119. [Google Scholar] [CrossRef]
- Sagheer, A.; Metwally, N. Communication via quantum neural network. In Proceedings of the 2010 Second World Congress on Nature and Biologically Inspired Computing (NaBIC), Fukuoka, Japan, 15–17 December 2010; pp. 418–422. [Google Scholar]
- Zidan, M.; Sagheer, A.; Metwally, N. An Autonomous Competitive Learning Algorithm using Quantum Hamming Neural Networks. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 788–792. [Google Scholar]
- Zhou, R.; Qin, L.; Jiang, N. Quantum perceptron network. In Proceedings of the International Conference on Artificial Neural Networks, Athens, Greece, 10–14 September 2006; Kollias, S.D., Stafylopatis, A., Duch, W., Oja, E., Eds.; Lecture Notes in Computer Science, 4131. Springer: Berlin/Heidelberg, Germany, 2006; pp. 651–657. [Google Scholar]
- Ventura, D.; Martinez, T. Quantum associative memory. Inf. Sci. 2000, 5124, 273–296. [Google Scholar] [CrossRef]
- Silva, A.J.D.; Ludermir, T.B.; Oliveria, W.R.D. Quantum perceptron over a field and neural network architecture seclection in a quantum computer. Neural Netw. 2016, 76, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Yuan, C. Quantum competition network model based on quantum entanglement. J. Comput. 2012, 7, 2312–2317. [Google Scholar] [CrossRef]
- Siomau, M. A quantum model for autonomous learning automata. Quantum Inf. Proc. 2014, 13, 1211–1221. [Google Scholar] [CrossRef] [Green Version]
- Zidan, M.; Abdel-Aty, A.-H.; El-shafei, M.; Feraig, M.; Al-Sbou, Y.; Eleuch, H.; Abdel-Aty, M. Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure. Appl. Sci. 2019, 9, 1277. [Google Scholar] [CrossRef]
- Lee, G. Quantum Computers Strive to Break Out of the Lab. IEEE Spectr. 2018. Available online: https://spectrum.ieee.org/computing/hardware/quantum-computers-strive-to-break-out-of-the-lab (accessed on 13 November 2018).
- Rosenblatt, F. The Perceptron-a Perceiving and Recognizing Automaton; Report 85-460-1; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1957. [Google Scholar]
- Altaisky, M. Quantum Neural Networks. arXiv 2001, arXiv:qunat-ph/0l07012. [Google Scholar]
- Fei, L.; Baoyu, Z. A study of quantum neural networks. In Proceedings of the IEEE Proc. of International Conference on Neural Networks and Signal Processing, Nanjing, China, 14–17 December 2003; Volume 1, pp. 539–542. [Google Scholar]
- Chuang, I.; Nielsen, M. Quantum Computation and Quantum Information; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Sanders, B.C. How to Build a Quantum Computer; IOP Publishing: Bristol, UK, 2017. [Google Scholar]
- Raudys, S. Evolution and generalization of a single neuron: I. Single layer perceptron as seven statistical classifiers. Neural Netw. 1998, 11, 283–296. [Google Scholar] [CrossRef]
- Raudys, S. Evolution and generalization of a single neuron: II. Complexity of statistical classifiers and sample size considerations. Neural Netw. 1998, 11, 297–313. [Google Scholar] [CrossRef]
- Omar, Y.A.; Yoo, P.D.; Muhaidat, S.; Karagiannidis, G.K.; Taha, K. Efficient Machine Learning for Big Data: A Review. Big Data Res. 2015, 2, 87–93. [Google Scholar] [Green Version]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th Annual Symposium on Theory of Computation, Philadelphia, PA, USA, 22–24 May1996; pp. 212–219. [Google Scholar]
- Jeswal, S.K.; Chakraverty, S. Recent Developments and Applications in Quantum Neural Network: A Review. Arch. Comput. Methods Eng. 2018, 1–15. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Charbon, E. A quantum-implementable neural network model. Quantum Inf. Proc. 2017, 16, 245. [Google Scholar] [CrossRef]
- Menneer, T. Quantum Artificial Neural Networks. Ph.D. Thesis, University of Exeter, Exeter, UK, 1998. [Google Scholar]
- Narayanan, A.; Menneer, T. Quantum artificial neural network architectures and components. Inf. Sci. 2000, 128, 231–255. [Google Scholar] [CrossRef]
- Gupta, S.; RKP, Z. Quantum neural networks. J. Comput. Syst. Sci. 2001, 63, 355–383. [Google Scholar] [CrossRef]
- Kouda, N.; Matsui, N.; Nishimura, H.; Peper, F. Qubit neural network and its learning efficiency. Neural Comput. Appl. 2005, 14, 114–121. [Google Scholar] [CrossRef]
- Schulda, M.; Sinayskiy, I.; Petruccionea, F. Simulating a perceptron on a quantum computer. Phys. Lett. A 2015, 379, 660–663. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Wang, J.; Pi, Y.; Yuan, Q. A novel ANN model based on quantum computational MAS theory. In Bio-Inspired Computational Intelligence and Applications; Li, K., Fei, M., Irwin, G., Ma, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4688, pp. 28–35. [Google Scholar]
- Bhattacharyya, S.; Bhattacharjee, S.; Mondal, N.K. A quantum backpropagation multilayer perceptron (QBMLP) for predicting iron adsorption capacity of calcareous soi lfrom aqueous solution. Appl. Soft Comput. 2015, 27, 299–312. [Google Scholar] [CrossRef]
- Yamamoto, A.Y.; Sundqvist, K.M.; Peng, L.; Harris, H.R. Simulation of a Multidimensional Input Quantum Perceptron. Quantum Inf. Proc. 2018, 17, 128. [Google Scholar] [CrossRef]
- Neto, F.M.; Ludermir, T.; De Oliveira, W.; Da Silva, A. Quantum Perceptron with Dynamic Internal Memory. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Liu, W.; Gao, P.; Wang, Y.; Wenbin, Y.; Zhang, M. A unitary weights based one-iteration quantum perceptron algorithm for non-ideal training sets. IEEE Access 2019, 7, 36854–36865. [Google Scholar] [CrossRef]
- Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Manju, A.; Nigam, M.J. Applications of quantum inspired computational intelligence: A survey. Artif. Intell. Rev. Arch. 2014, 42, 79–156. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A. High-Capacity Quantum Associative Memories. J. Appl. Math. Phys. 2016, 4. [Google Scholar] [CrossRef]
- Portuga, R. Walks and Search Algorithms; Springer: New York, NY, USA, 2013. [Google Scholar]
- Horn, R.; Johnson, C. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1999; Volume 13, pp. 1211–1221. [Google Scholar]
- UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets.html (accessed on 13 November 2018).
- Xiao, L.; Shang, P.; Tong, H.; Li, X.; Cao, M. A hybrid quantum-inspired neural networks with sequence inputs. Neurocomputing 2013, 117, 81–90. [Google Scholar]
- Ou, G.; Murphey, Y.L. Multi-class pattern Classification using neural networks. Pattern Recognit. 2007, 40, 4–18. [Google Scholar] [CrossRef]
- Karabatak, M.; Ince, M.C. An Expert system for detection of breast Cancer based on association rules and neural network. Expert Syst. Appl. 2009, 36, 3465–3469. [Google Scholar] [CrossRef]
- Sagheer, A.; Zidan, M. Autonomous Quantum Perceptron Neural Network. arXiv 2013, arXiv:1312.4149. [Google Scholar]
- NaqviTallh, S.; Akram, T.; Iqbal, S.; Ali, S.; Kamran, M.; Muhammad, N. A dynamically reconfigurable logic cell: From artificial neural networks to quantum-dot cellular automata. Appl. Nanosci. 2018, 8, 89–103. [Google Scholar]











| Name of Algorithm | APM | AQP [20] | QP [16] |
|---|---|---|---|
| No. of iterations | 1 | 1 | 16 |
| No. of training patterns | 3 | 4 | 4 |
| Name of Dataset | IRIS | Breast Cancer | Types of Glass | Wine Vintage |
|---|---|---|---|---|
| No. of attributes | 4 | 9 | 9 | 13 |
| No. of classes | 3 | 2 | 2 | 3 |
| No. of training examples (N) | 48% | 1.48% | 16.85% | 25% |
| No. of patterns | 150 | 699 | 214 | 178 |
| Name of Algorithm | IRIS | Breast Cancer | Types of Glass | Wine Vintage |
|---|---|---|---|---|
| The Proposed Perceptron APM | 1 | 1 | 1 | 1 |
| Multilayer Perceptron (MLP) | 4-5-3 | 9-26-2 | 9-14-2 | 13-10-3 |
| Name of Algorithm | Non-Linearity Property | IRIS | Breast Cancer | Types of Glass | Wine Vintage |
|---|---|---|---|---|---|
| Proposed model APM | yes | 99.6 | 98.8 | 100 | 100 |
| 1- Multilayer perceptron | yes | 96 | 48.4 | 61.1 | 93.9 |
| 2- Linear discriminant | no | 94.7 | 96.6 | 90.7 | 100 |
| 3- Quadratic discriminant | yes | 93.3 | 48.4 | 89.7 | 100 |
| 4- LogitBoost | yes | 94.7 | 65 | 62.2 | 95.3 |
| 5- Naive Bayes | yes | 96 | 64.3 | 48.9 | 93.9 |
| 6- K* Classifier | yes | 94.7 | 49.1 | 73.3 | 91.9 |
| 7- Bagging | yes | 92 | 97.1 | 94.4 | 100 |
| 8- MetaClassifier | yes | 94.7 | 48.4 | 55.5 | 95.9 |
| 9- Decision table | yes | 94.7 | 70.7 | 91.6 | 100 |
| 10- Random forest | yes | 94.7 | 30.4 | 77.8 | 91.9 |
| 11- Logistic model Trees | no | 94.7 | 65 | 65.5 | 95.3 |
| 12- Linear SVM | no | 95.3 | 94.1 | 87.9 | 100 |
| 13- Fine KNN | yes | 96 | 94.1 | 93.5 | 100 |
| 14- AdaBoost | yes | 33.3 | 91.2 | 76.6 | 37.5 |
| 15- Subspace | yes | 94.7 | 91.2 | 95.3 | 100 |
| Name of Algorithm | IRIS | Breast Cancer | Types of Glass | Wine Vintage |
|---|---|---|---|---|
| Type of learner | NN | NN | NN | NN |
| Number of learners | 30 | 30 | 30 | 30 |
| Subspace Dimensions | 2 | 7 | 5 | 7 |
| Algorithm Name | IRIS | Breast Cancer | Types of Glass | Wine Vintage |
|---|---|---|---|---|
| APM | 0.06 | 0.08 | 0.05 | 0.07 |
| Linear Discriminant | 0.23 | 0.19 | 0.22 | 0.21 |
| Quadratic Discriminant | 0.18 | 1.87 | 0.19 | 0.13 |
| Bagging | 0.72 | 0.8 | 0.86 | 0.83 |
| Decision Table | 0.89 | 1.05 | 0.7 | 0.34 |
| Linear SVM | 1.14 | 0.7 | 0.26 | 0.35 |
| Fine KNN | 0.26 | 0.42 | 0.24 | 0.23 |
| AdaBoost | 0.31 | 1.56 | 0.32 | 0.23 |
| Subspace | 1.14 | 1.29 | 0.97 | 0.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagheer, A.; Zidan, M.; Abdelsamea, M.M. A Novel Autonomous Perceptron Model for Pattern Classification Applications. Entropy 2019, 21, 763. https://doi.org/10.3390/e21080763
Sagheer A, Zidan M, Abdelsamea MM. A Novel Autonomous Perceptron Model for Pattern Classification Applications. Entropy. 2019; 21(8):763. https://doi.org/10.3390/e21080763
Chicago/Turabian StyleSagheer, Alaa, Mohammed Zidan, and Mohammed M. Abdelsamea. 2019. "A Novel Autonomous Perceptron Model for Pattern Classification Applications" Entropy 21, no. 8: 763. https://doi.org/10.3390/e21080763
APA StyleSagheer, A., Zidan, M., & Abdelsamea, M. M. (2019). A Novel Autonomous Perceptron Model for Pattern Classification Applications. Entropy, 21(8), 763. https://doi.org/10.3390/e21080763






