Modelling Thermally Induced Non-Equilibrium Gas Flows by Coupling Kinetic and Extended Thermodynamic Methods
Abstract
:1. Introduction
2. Extended Thermodynamic Governing Equations
3. Kinetic Equation and the Shakhov Model
4. Hybrid Algorithm of Coupling the Moment Equations and the Kinetic Equation (HYBR)
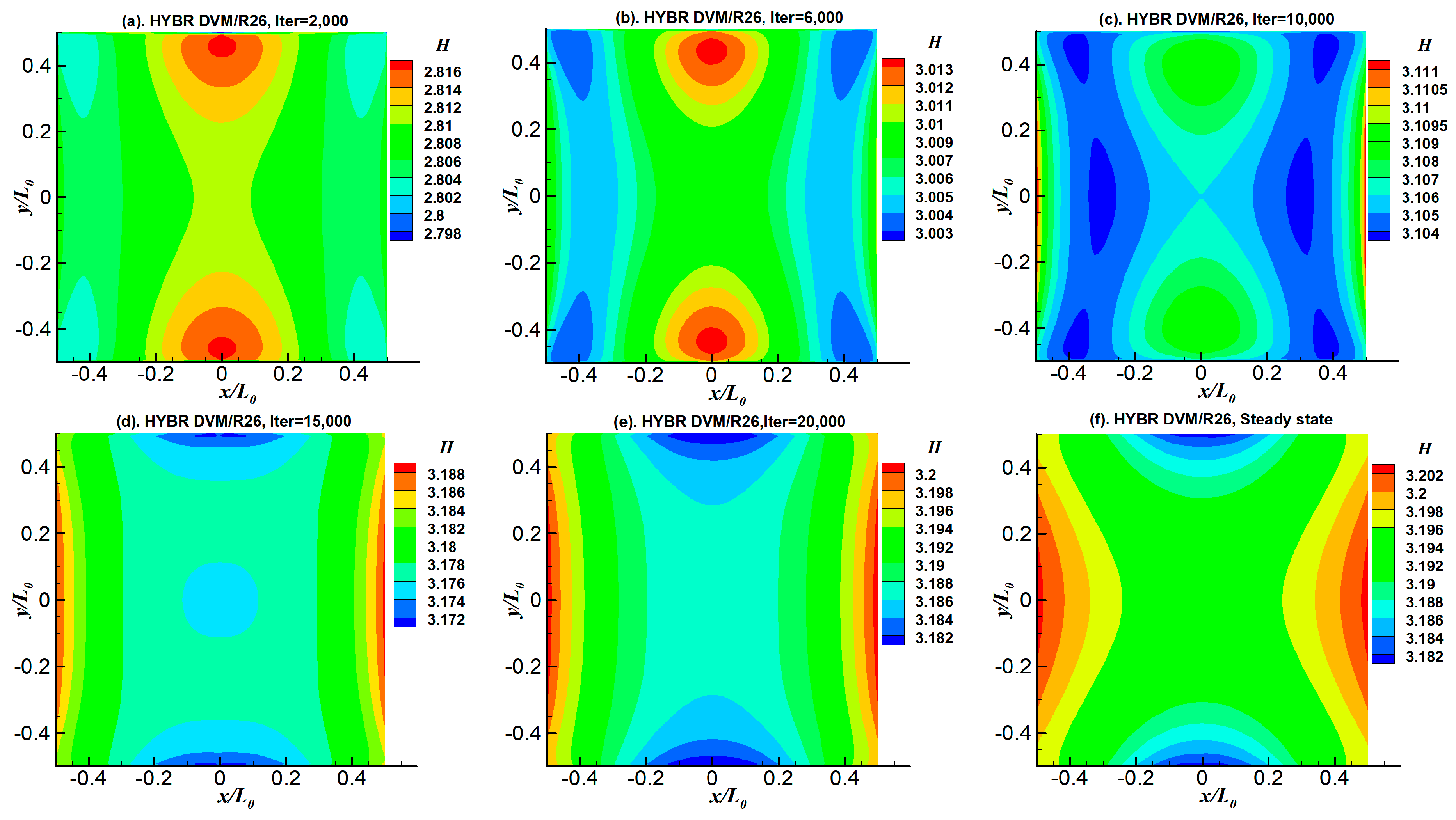
5. Entropy and H-Theorem
6. Numerical Test Cases
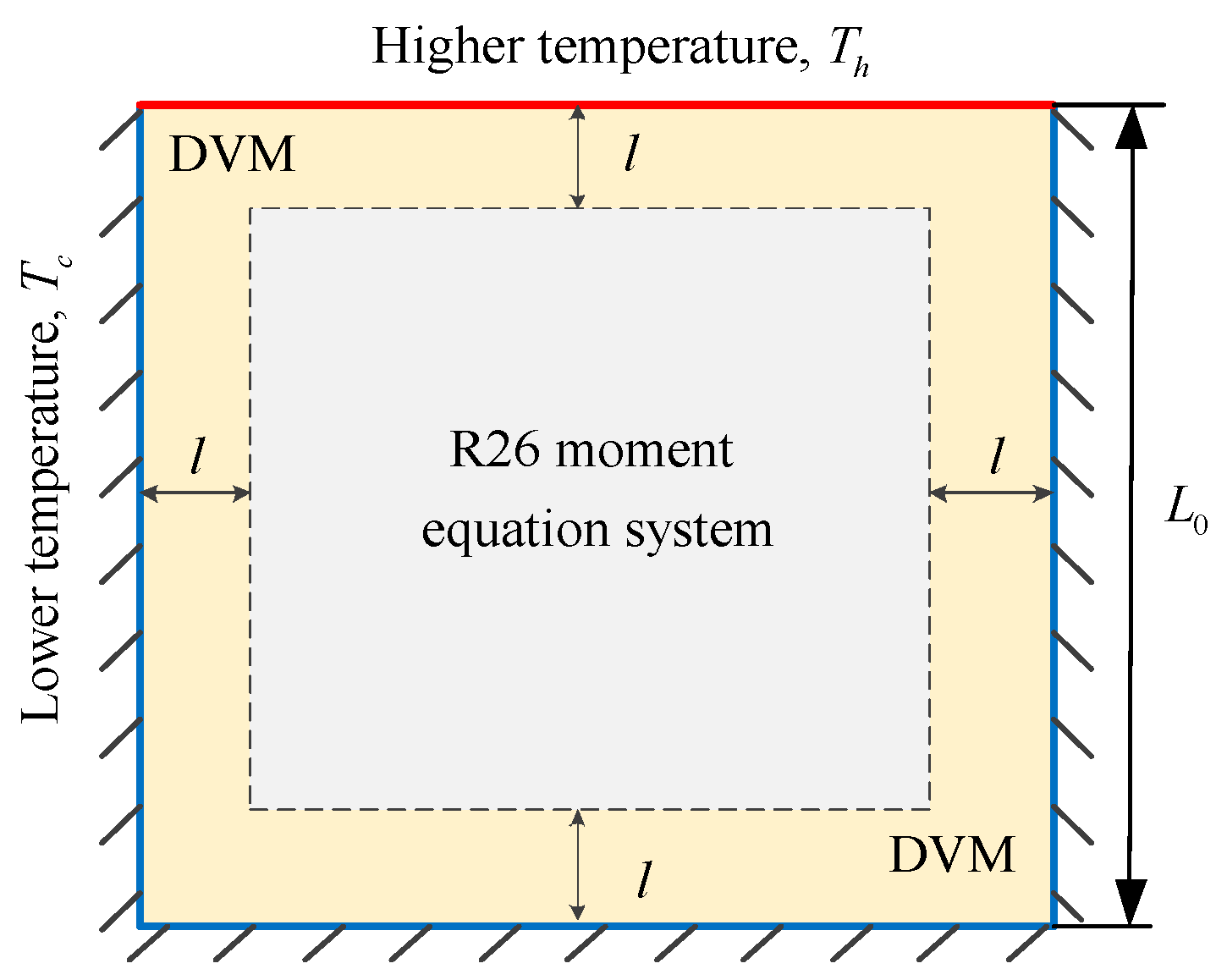
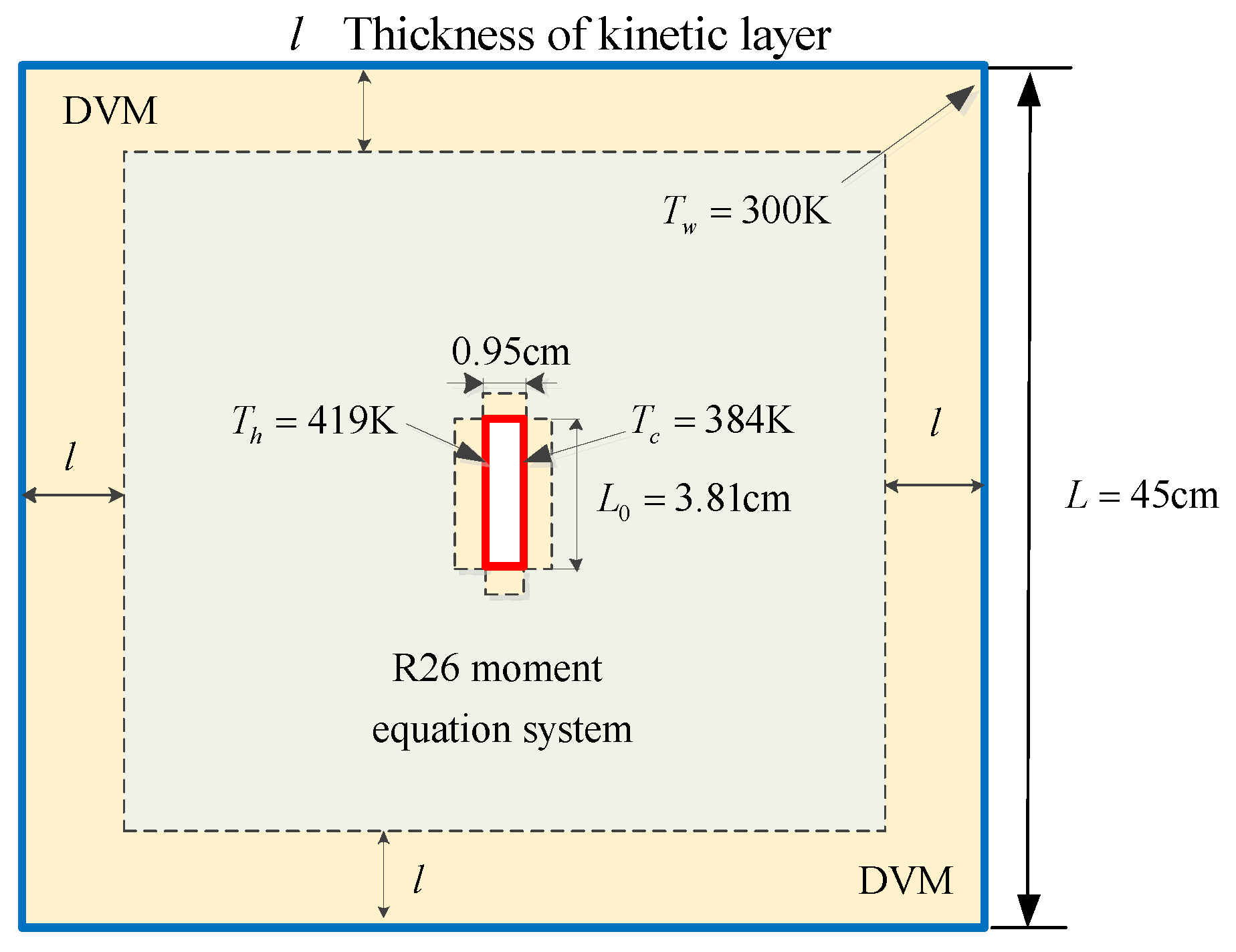
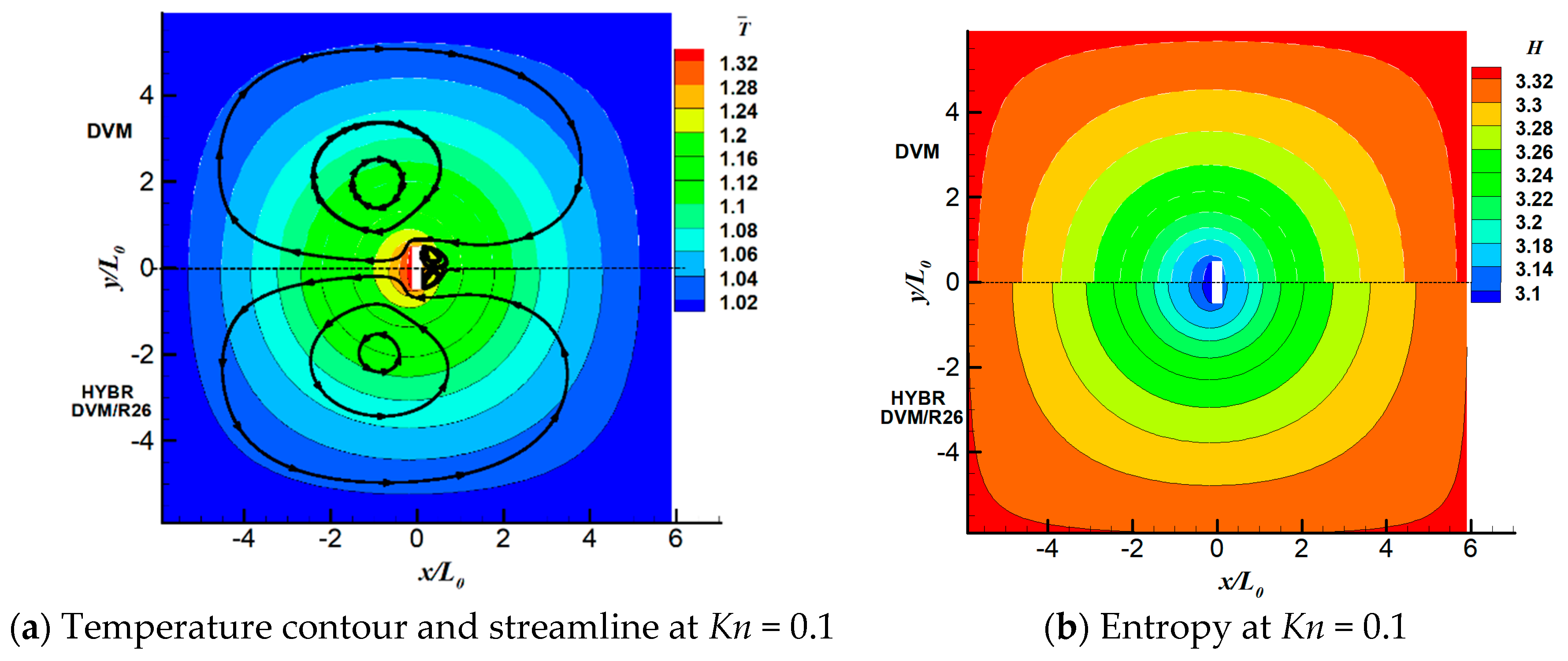
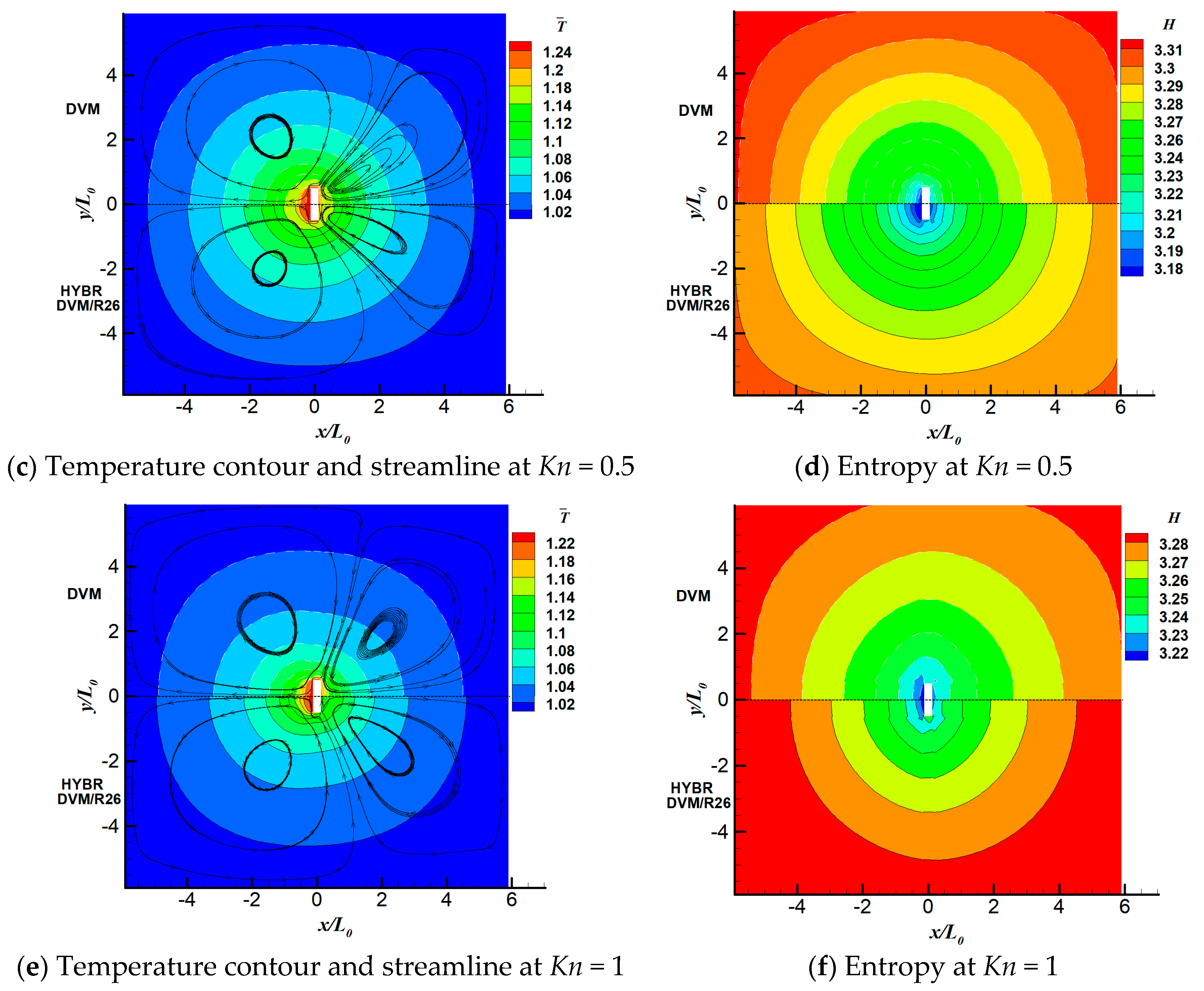
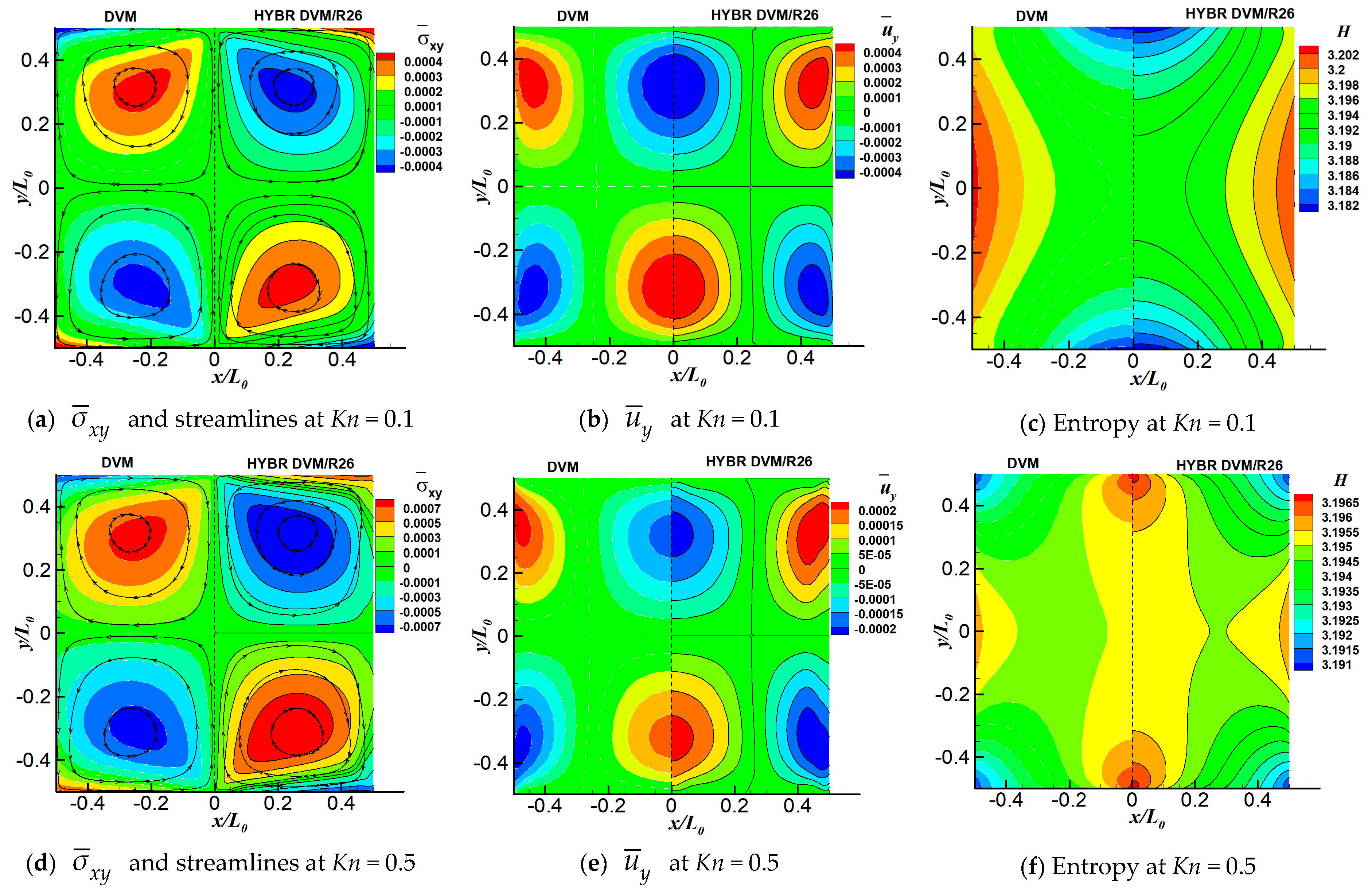
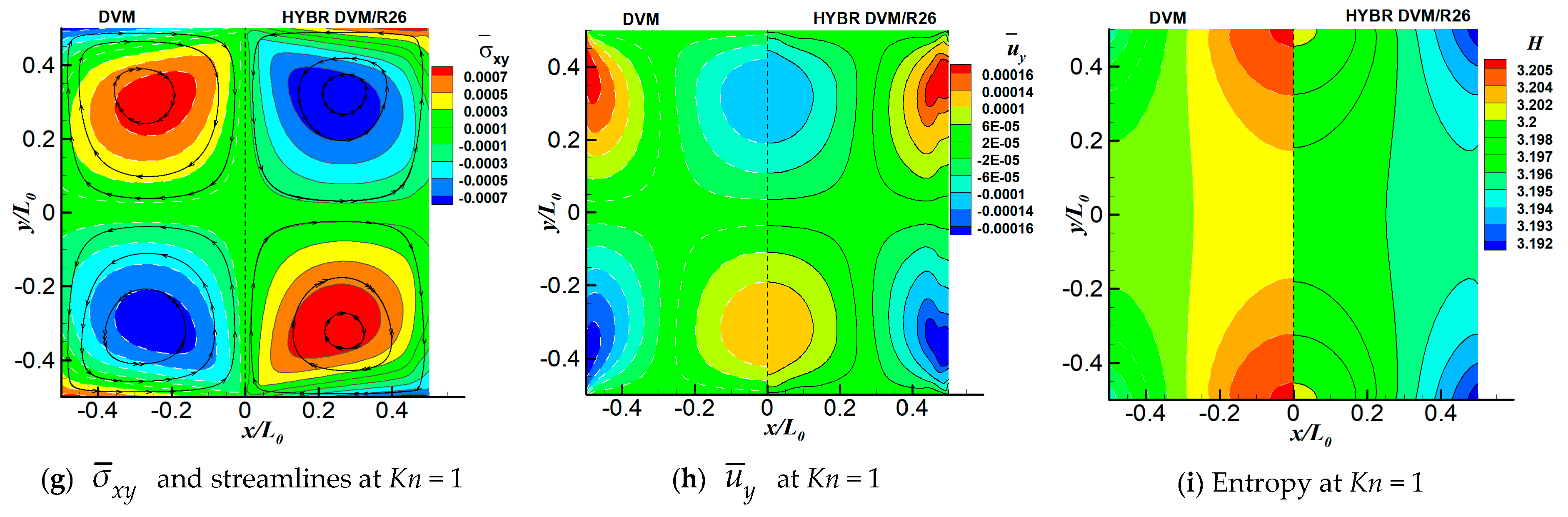
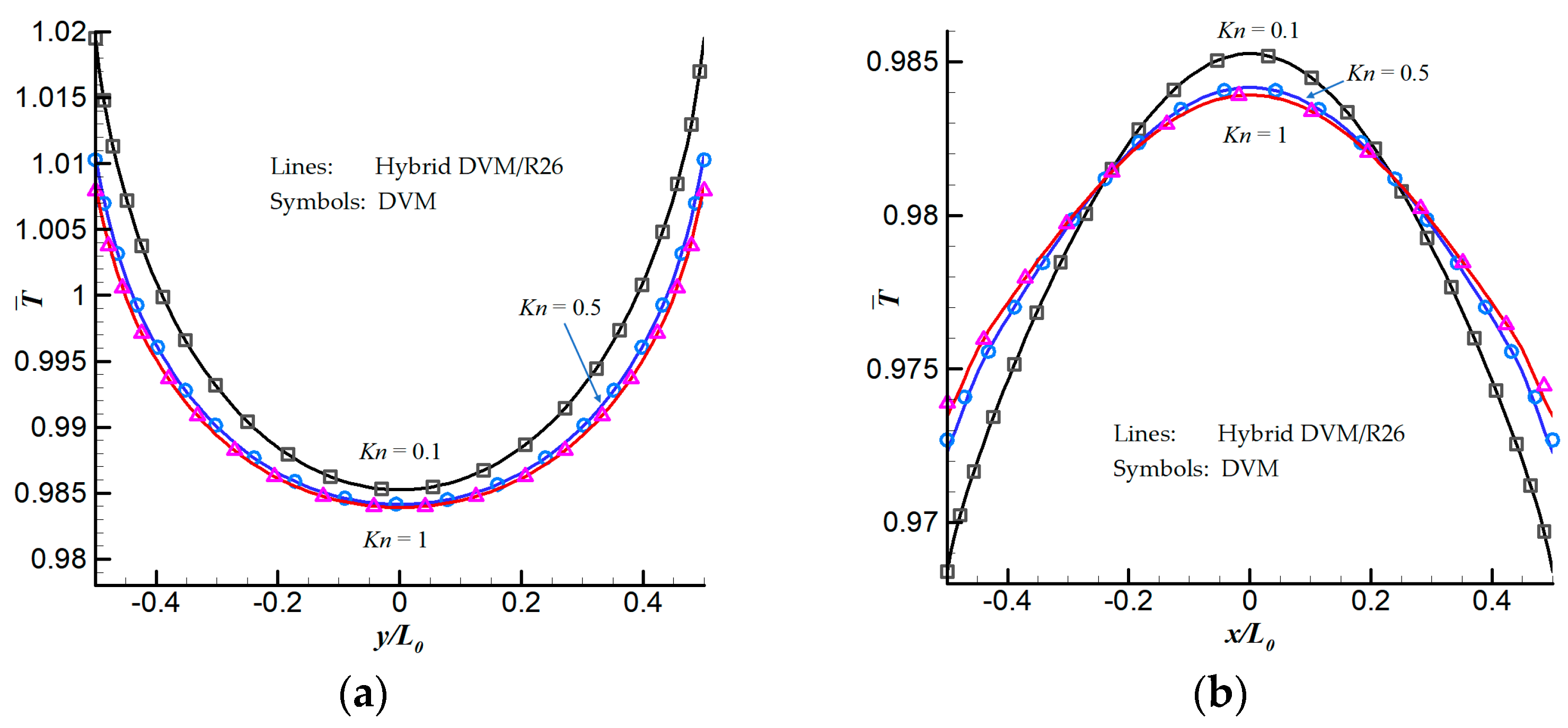
6.1. 2D Thermal Cavity Flow Induced by Temperature Discontinuity
6.2. Radiometric Flow
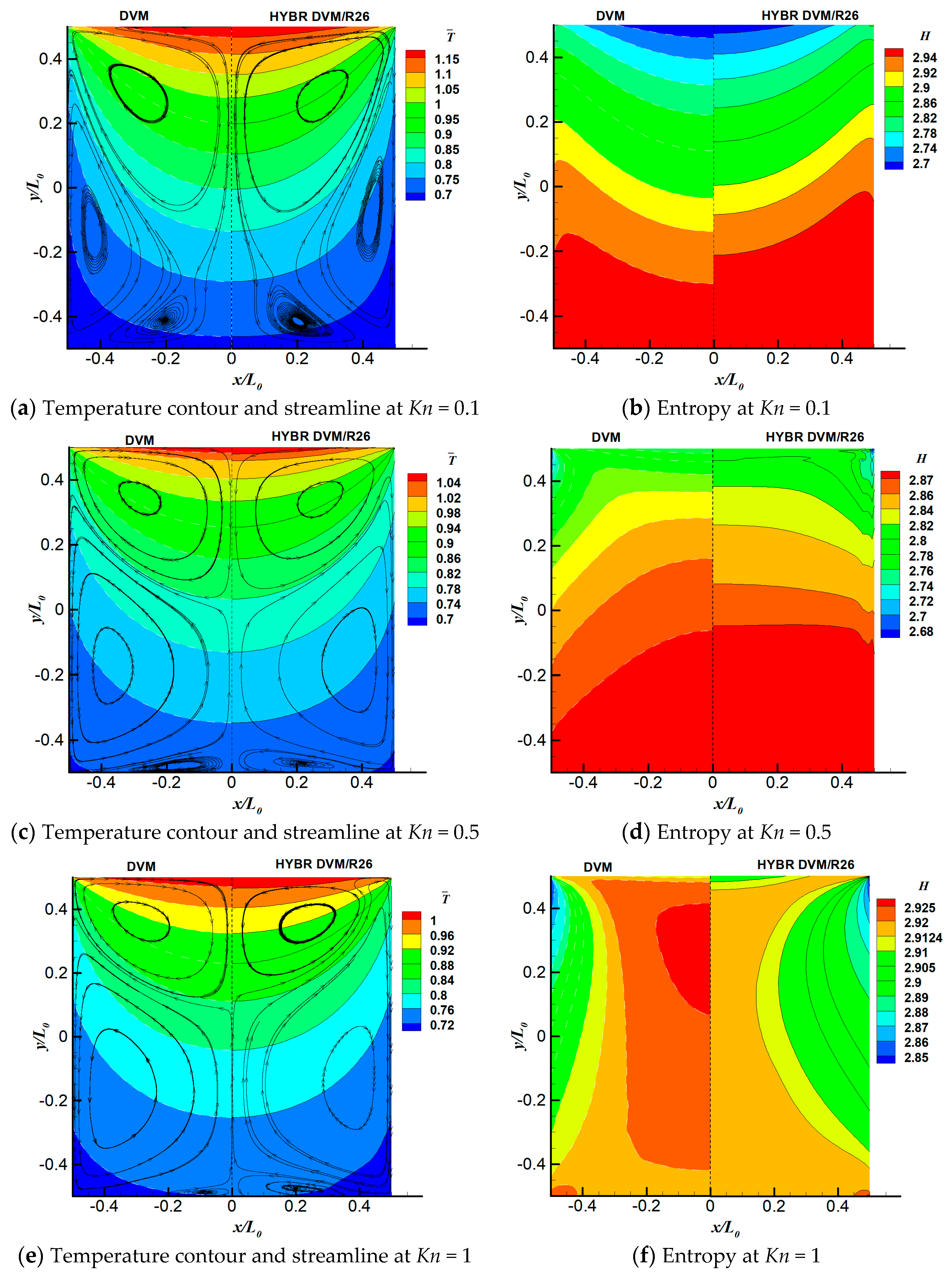
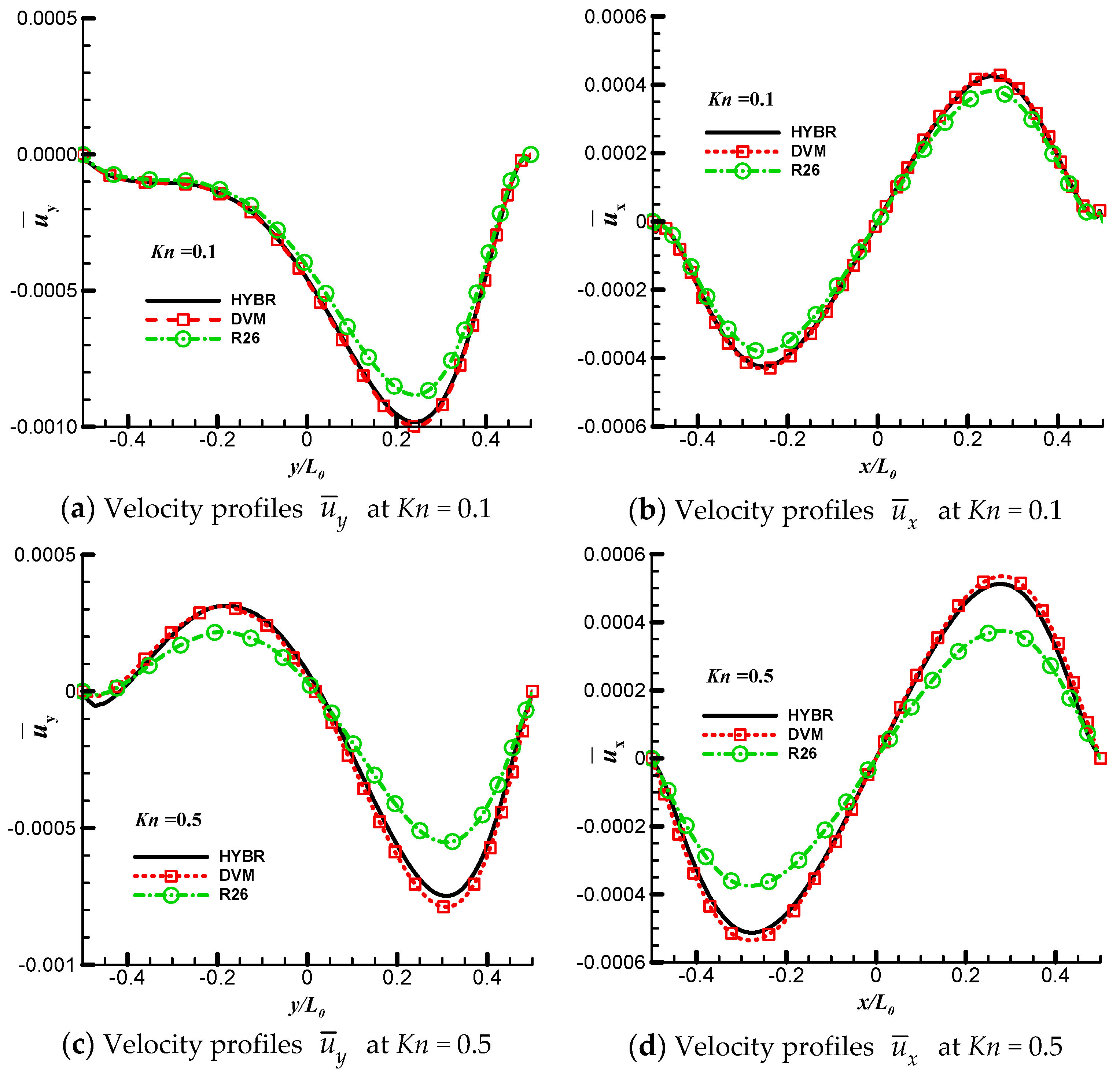
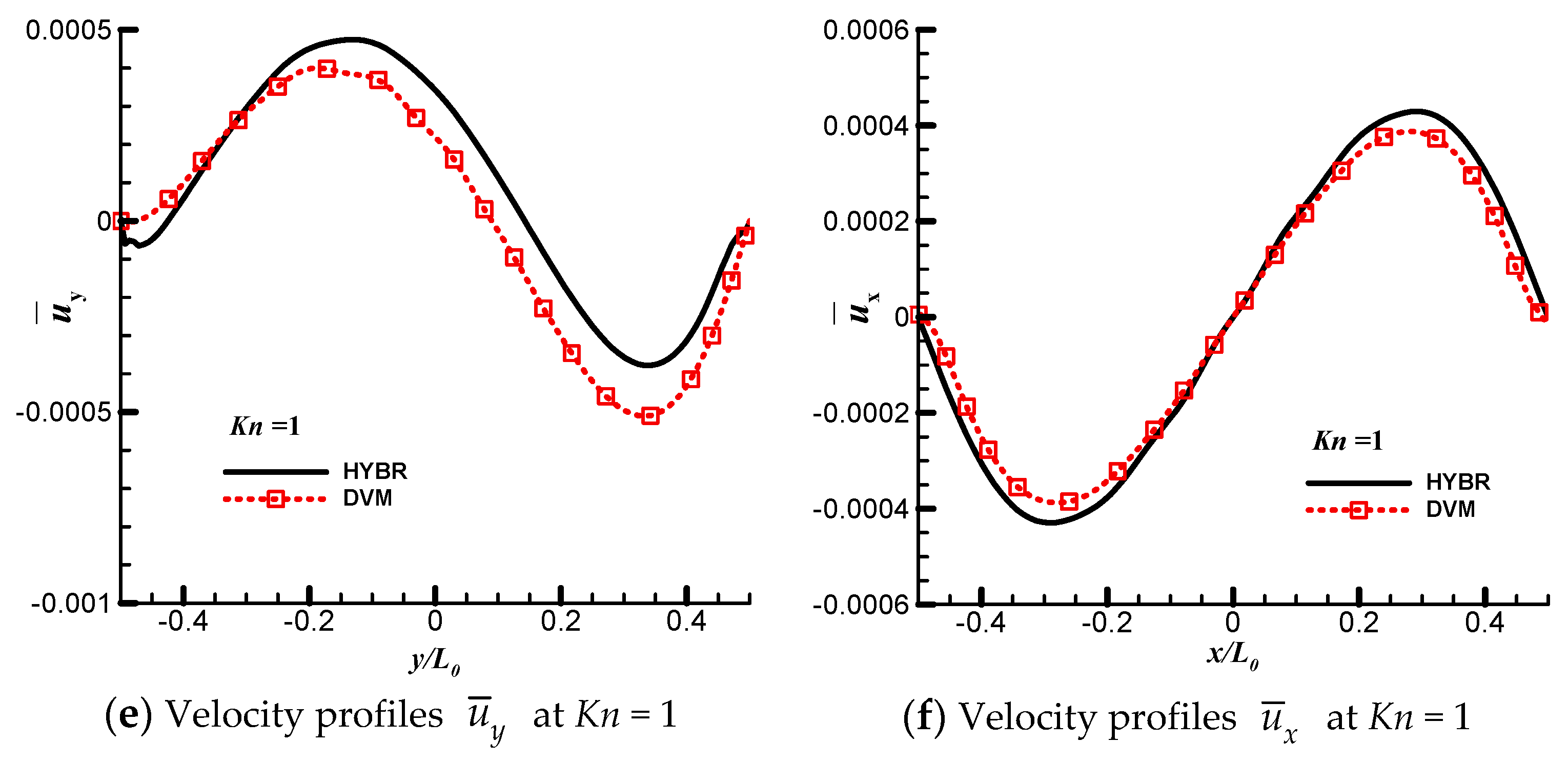
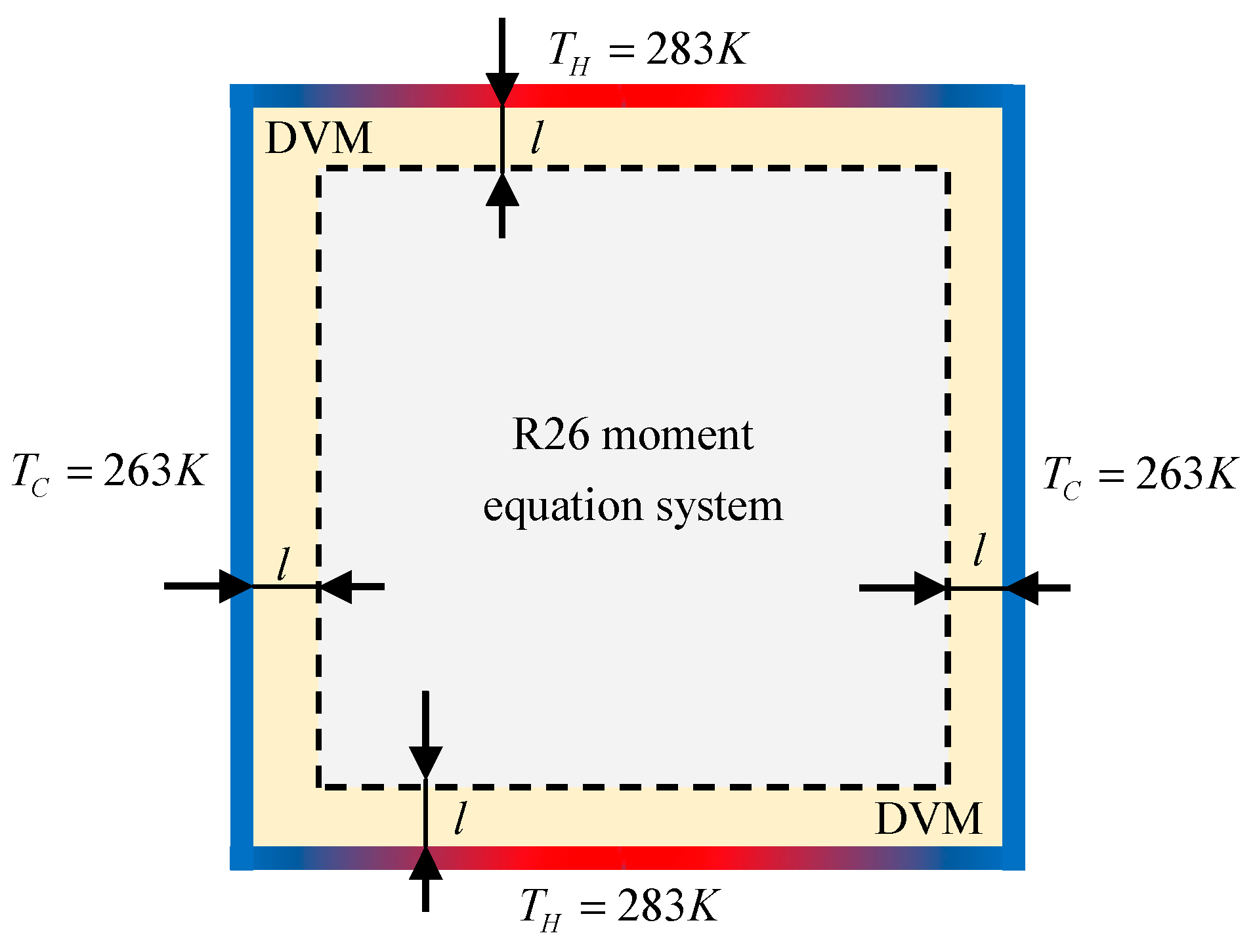
6.3. 2D Thermal Cavity Flow Induced by the Temperature Gradients
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Source Terms in the Moment Equation (3)
References
- Ketsdever, A.; Gimelshein, N.; Gimelshein, S.; Selden, N. Radiometric phenomena: From the 19th to the 21st century. Vacuum 2012, 86, 1644–1662. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, X.; Guo, Z. Thermally induced rarefied gas flow in a three-dimensional enclosure with square cross-section. Phys. Rev. Fluids 2017, 2, 123402. [Google Scholar] [CrossRef] [Green Version]
- Shahabi, V.; Baier, T.; Roohi, E.; Hardt, S. Thermally induced gas flows in ratchet channels with diffuse and specular boundaries. Sci. Rep. 2017, 7, 41412. [Google Scholar] [CrossRef] [PubMed]
- Sone, Y. Kinetic Theory and Fluid Dynamics; Springer Science & Business Media, LLC.: New York, NY, USA, 2002; pp. 123–160. [Google Scholar]
- Sheng, Q.; Tang, G.H.; Gu, X.J.; Emerson, D.R.; Zhang, Y.H. Simulation of thermal transpiration flow using a high-order moment method. Int. J. Mod. Phys. C 2014, 25, 1450061. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Cárdenas, M.R.; Perrier, P.; Graur, I.; Niimi, T. Thermal transpiration flow through a single rectangular channel. J. Fluid Mech. 2014, 744, 169–182. [Google Scholar] [CrossRef]
- Zhu, L.; Guo, Z. Application of discrete unified gas kinetic scheme to thermally induced nonequilibrium flows. Comput. Fluids 2017, 103613. [Google Scholar] [CrossRef]
- Strongrich, A.; Pikus, A.; Sebastião, I.B.; Alexeenko, A. Microscale in-plane Knudsen radiometric actuator: Design, characterization, and performance modelling. J. Microelectromech. Syst. 2017, 26, 528–538. [Google Scholar] [CrossRef]
- Vargo, S.E.; Muntz, E.P. Initial results from the first MEMS fabricated thermal transpiration-driven vacuum pump. AIP Conf. Proc. 2001, 585, 502–509. [Google Scholar]
- Nallapu, R.T.; Tallapragada, A.; Thangavelautham, J. Radiometric Actuators for Spacecraft Attitude Control. arXiv 2017, arXiv:1701.07545. [Google Scholar]
- Liu, J.; Gupta, N.K.; Wise, K.D.; Gianchandani, Y.B.; Fan, X. Demonstration of motionless Knudsen pump based micro-gas chromatography featuring micro-fabricated columns and on-column detectors. Lab Chip 2011, 11, 3487–3492. [Google Scholar] [CrossRef]
- Sugimoto, H.; Hibino, M. Numerical analysis on gas separator with thermal transpiration in micro channels. AIP Conf. Proc. 2012, 1501, 794–801. [Google Scholar]
- Rojas-Cárdenas, M.; Graur, I.; Perrier, P.; Meolans, J.G. Thermal transpiration flow: A circular cross-section microtube submitted to a temperature gradient. Phys. Fluids 2011, 23, 031702. [Google Scholar] [CrossRef]
- Rojas-Cárdenas, M.; Graur, I.; Perrier, P.; Meolans, J.G. An experimental and numerical study of the final zero-flow thermal transpiration stage. J. Therm. Sci. Tech. 2012, 7, 437–452. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, R.; Xu, K. Discrete unified gas kinetic scheme for all Knudsen number flows. II. Thermal compressible case. Phys. Rev. E 2015, 91, 033313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Clarendon Press: Oxford, UK, 1994; pp. 46–98. [Google Scholar]
- Goldstein, D.; Sturtevant, B.; Broadwell, J.E. Investigations of the motion of discrete-velocity gases. Prog. Astronaut. Aeronaut. 1989, 118, 100–117. [Google Scholar]
- Sone, Y. Flows induced by temperature fields in a rarefied gas and their ghost effect on the behavior of a gas in the continuum limit. Annu. Rev. Fluid Mech. 2000, 32, 779–811. [Google Scholar] [CrossRef]
- Chapman, S. On the law of distribution of molecular velocities, and the theory of viscosity and thermal conduction, in a non-uniform simple monatomic gas. Philos. Trans. R. Soc. A 1916, 216, 538–548. [Google Scholar] [CrossRef]
- Enskog, D. Kinetische Theorie der Vorgänge in mässig verdünnten Gasen; Almqvist and Wiksells: Uppsala, Sweden, 1917. (In German) [Google Scholar]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Grad, H. Asymptotic Theory of the Boltzmann Equation. Phys. Fluids 1963, 6, 147–181. [Google Scholar] [CrossRef]
- Grad, H. On the kinetic theory of rarefied gases. Comm. Pure Appl. Math. 1949, 2, 331–407. [Google Scholar] [CrossRef]
- Struchtrup, H.; Torrilhon, M. Regularization of Grad’s 13 moment equations: Derivation and linear analysis. Phys. Fluids 2003, 15, 2668–2680. [Google Scholar] [CrossRef]
- Gu, X.-J.; Emerson, D.R. A computational strategy for the regularized 13 moment equations with enhanced wall-boundary conditions. J. Comput. Phys. 2007, 225, 263–283. [Google Scholar] [CrossRef]
- Struchtrup, H.; Torrilhon, M.H. Theorem, regularization and boundary conditions for linearized 13 moment equations. Phys. Rev. Lett. 2007, 99, 014502. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, J.C. On stresses in rarified gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. A 1879, 170, 231–256. [Google Scholar]
- Gu, X.-J.; Emerson, D.R. A high-order moment approach for capturing non-equilibrium phenomena in the transition regime. J. Fluid Mech. 2009, 636, 177–216. [Google Scholar] [CrossRef]
- Gu, X.-J.; Barber, R.W.; John, B.; Emerson, D.R. Non-equilibrium effects on flow past a circular cylinder in the slip and early transition regime. J. Fluid Mech. 2019, 860, 654–681. [Google Scholar] [CrossRef]
- Gu, X.-J.; Emerson, D.R.; Tang, G.-H. Analysis of the slip coefficient and defect velocity in the Knudsen layer of a rarefied gas using the linearized moment equations. Phys. Rev. E 2010, 81, 016313. [Google Scholar] [CrossRef] [PubMed]
- Struchtrup, H. Macroscopic Transport Equations for Rarefied Gas Flows; Springer: New York, NY, USA, 2005. [Google Scholar]
- Young, J.B. Calculation of Knudsen layers and jump conditions using the linearised G13 and R13 moment methods. Int. J. Heat Mass Transf. 2011, 54, 2902–2912. [Google Scholar] [CrossRef]
- Shakhov, E.M. Generalization of the Krook kinetic relaxation equation. Fluid Dyn. 1968, 3, 95–96. [Google Scholar] [CrossRef]
- Yang, W.; Gu, X.-J.; Emerson, D.R.; Wu, L.; Zhang, Y.; Tang, S. A Hybrid Approach Coupling Discrete Velocity Method and Moment Method for Rarefied Gas Flows. J. Comput. Phys. 2019. submitted. [Google Scholar]
- Wu, L.; White, C.; Scanlon, T.J.; Reese, J.M.; Zhang, Y. Deterministic numerical solutions of the Boltzmann equation using the fast spectral method. J. Comput. Phys. 2013, 250, 27–52. [Google Scholar] [CrossRef] [Green Version]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corporation: Washington, DC, USA, 1980; pp. 113–135. [Google Scholar]
- Tang, G.H.; Zhai, G.X.; Tao, W.Q.; Gu, X.J.; Emerson, D.R. Extended thermodynamic approach for non-equilibrium gas flow. Commun. Comput. Phys. 2013, 13, 1330–1356. [Google Scholar] [CrossRef]
- Wu, L.; Ho, M.T.; Germanou, L.; Gu, X.J.; Liu, C.; Xu, K.; Zhang, Y.H. On the apparent permeability of porous media in rarefied gas flows. J. Fluid Mech. 2017, 822, 398–417. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.B.; Tang, G.H.; Sheng, Q.; Gu, X.J.; Emerson, D.R.; Zhang, Y.H. Knudsen’s permeability correction for gas flow in tight porous media using the R26 moment method. J. Porous Media 2017, 20, 787–805. [Google Scholar] [CrossRef]
- Grad, H. Note on N-dimensional Hermite polynomials. Commun. Pure Appl. Math. 1949, 2, 325–330. [Google Scholar] [CrossRef]
- Cercignani, C. The Boltzmann Equation and Its Applications; Springer: New York, NY, USA, 1988. [Google Scholar]
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]

| 1 | 1 | 1, 0 | 1, 0 | 1, 0 | 1, 0, 0 | 1, 0, 0 |
| Computational Memory (GB) | Computational Time (Minutes) | |||
|---|---|---|---|---|
| Kn = 0.1 | Kn = 0.5 | Kn = 1.0 | ||
| DVM | 11.80 | 452 | 204 | 128 |
| Hybrid DVM/R26 | 3.53 | 55 | 78 | 96 |
| Computational Memory (GB) | Computational Time (Minutes) | |||
|---|---|---|---|---|
| Kn = 0.1 | Kn = 0.5 | Kn = 1.0 | ||
| DVM | 42.50 | 983 | 503 | 324 |
| Hybrid DVM/R26 | 10.01 | 168 | 243 | 289 |
| Computational Memory (GB) | Computational Time (Minutes) | |||
|---|---|---|---|---|
| Kn = 0.1 | Kn = 0.5 | Kn = 1.0 | ||
| DVM | 11.22 | 512 | 237 | 156 |
| Hybrid DVM/R26 | 3.53 | 68 | 93 | 126 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Gu, X.-J.; Emerson, D.R.; Zhang, Y.; Tang, S. Modelling Thermally Induced Non-Equilibrium Gas Flows by Coupling Kinetic and Extended Thermodynamic Methods. Entropy 2019, 21, 816. https://doi.org/10.3390/e21080816
Yang W, Gu X-J, Emerson DR, Zhang Y, Tang S. Modelling Thermally Induced Non-Equilibrium Gas Flows by Coupling Kinetic and Extended Thermodynamic Methods. Entropy. 2019; 21(8):816. https://doi.org/10.3390/e21080816
Chicago/Turabian StyleYang, Weiqi, Xiao-Jun Gu, David R. Emerson, Yonghao Zhang, and Shuo Tang. 2019. "Modelling Thermally Induced Non-Equilibrium Gas Flows by Coupling Kinetic and Extended Thermodynamic Methods" Entropy 21, no. 8: 816. https://doi.org/10.3390/e21080816
APA StyleYang, W., Gu, X.-J., Emerson, D. R., Zhang, Y., & Tang, S. (2019). Modelling Thermally Induced Non-Equilibrium Gas Flows by Coupling Kinetic and Extended Thermodynamic Methods. Entropy, 21(8), 816. https://doi.org/10.3390/e21080816




