Information Theoretic Multi-Target Feature Selection via Output Space Quantization †
Abstract
1. Introduction
2. Background on Information Theoretic Multi-Target FS
2.1. Deriving Criteria via Maximum Likelihood Maximization Framework
- Joint-JMI
- does not make any assumptions and deals with the joint random variable . This corresponds to the Label Powerset (LP) transformation in the multi-label literature. The main limitation of this method is that is high dimensional. For example, in multi-label problems we have up to distinct labelsets [11], which makes it difficult to estimate MI expressions reliably.
- Single-JMI
- deals with each variable independently of the others. This corresponds to the Binary Relevance (BR) transformation in the multi-label literature. The main limitation of this method is that by making the full independence assumption it ignores possible useful information on how the targets interact with each other.
2.2. Other Information Theoretic Criteria
3. A Novel Framework to Take into Account Target Dependencies
3.1. Transforming Output Space via Quantization to Account for Target Dependencies
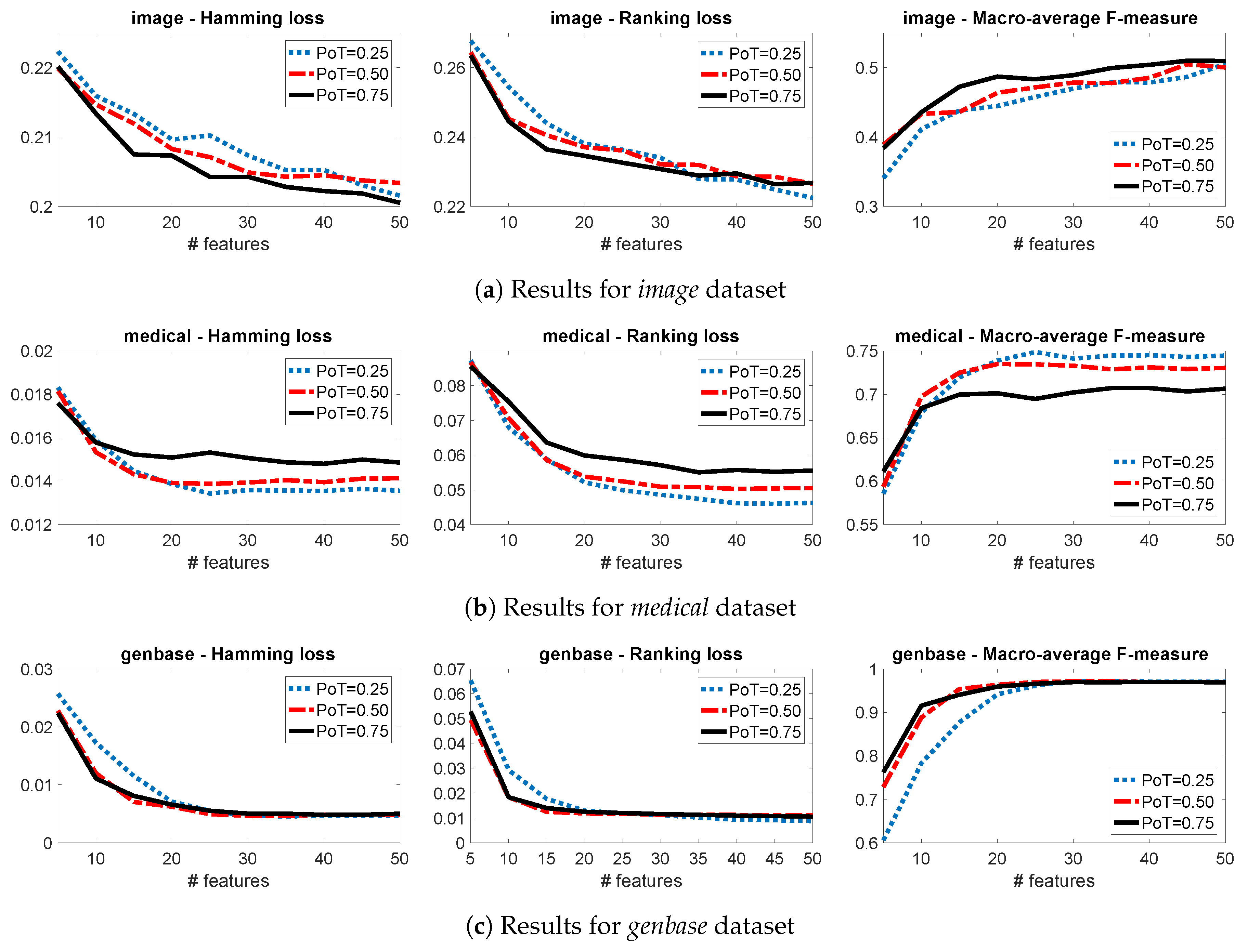
- 1st Step—Generate Groups of Target Variables, Using PoT Parameter
- 2nd Step—Low-dimensional Approximations via Quantization, Using NoC Parameter
| Algorithm 1 Forward FS with our Group-JMI criterion | |
| Input: Dataset , parameters PoT and NoC and the number of features to be selected K. | |
| Output: List of top-K features Xθ | |
| 1: | ▹ Set of candidate features |
| 2: Set to empty list | ▹ List of selected features |
| 3: for to m | ▹ Output transformation (where m is the number of target variables) |
| 4: Use PoT to generate a random subset of targets: | |
| 5: Derive from the cluster indices: | |
| 6: end for | |
| 7: for to K do | |
| 8: Let maximise: | |
| 9: | ▹ Our scoring criterion |
| 10: | ▹ Add feature to the list |
| 11: | ▹ Remove feature from the candidate set |
| 12: end for | |
3.2. Theoretical Analysis
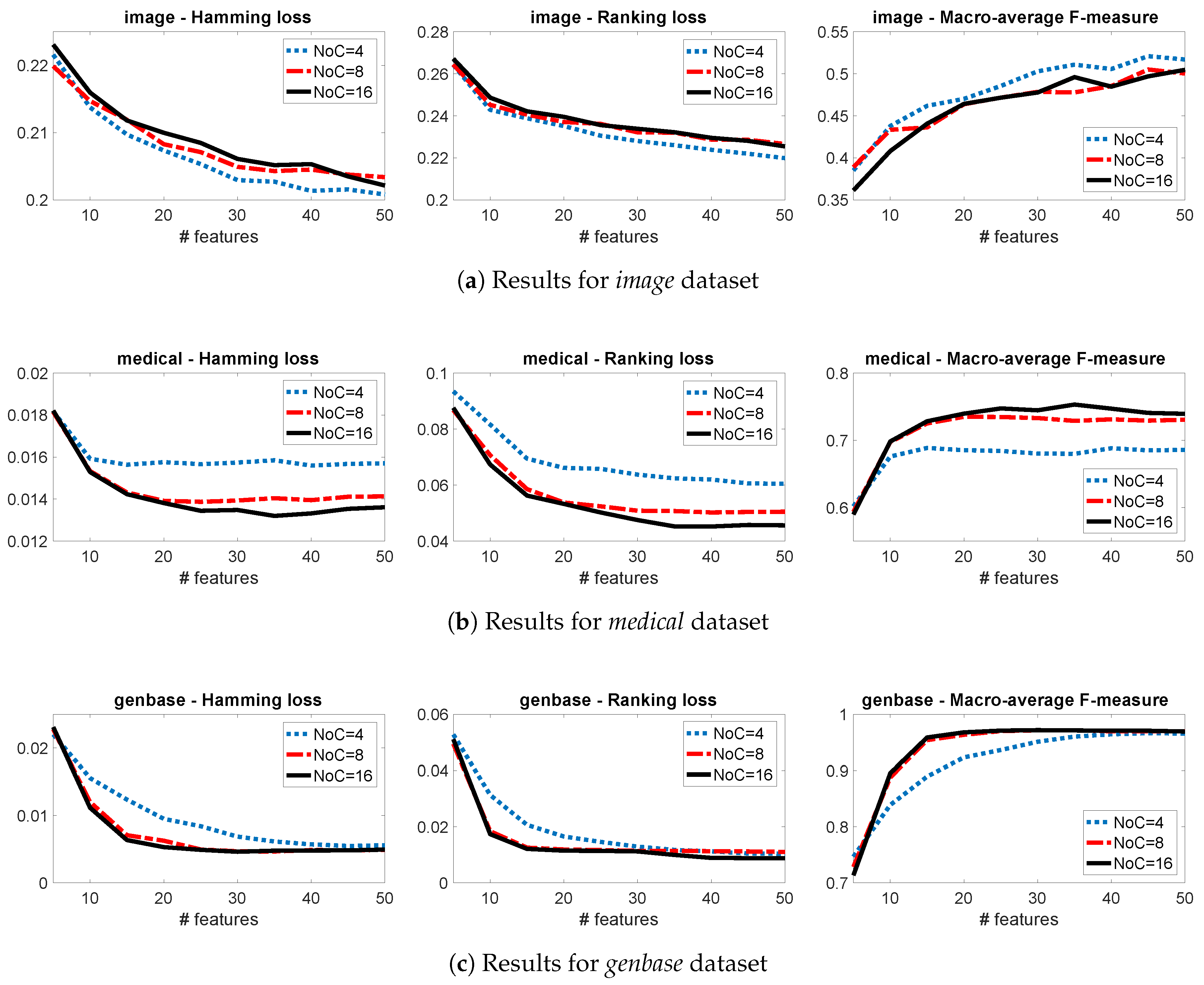
3.3. Sensitivity Analysis
3.4. A Group-JMI Criterion That Captures Various High-Order Target Interactions
4. Experiments with Multi-Label Data
4.1. Comparing Group-JMI-Rand with Other JMI Criteria
4.2. Comparing Group-JMI-Rand with State-of-the-Art Information Theoretic FS Criteria
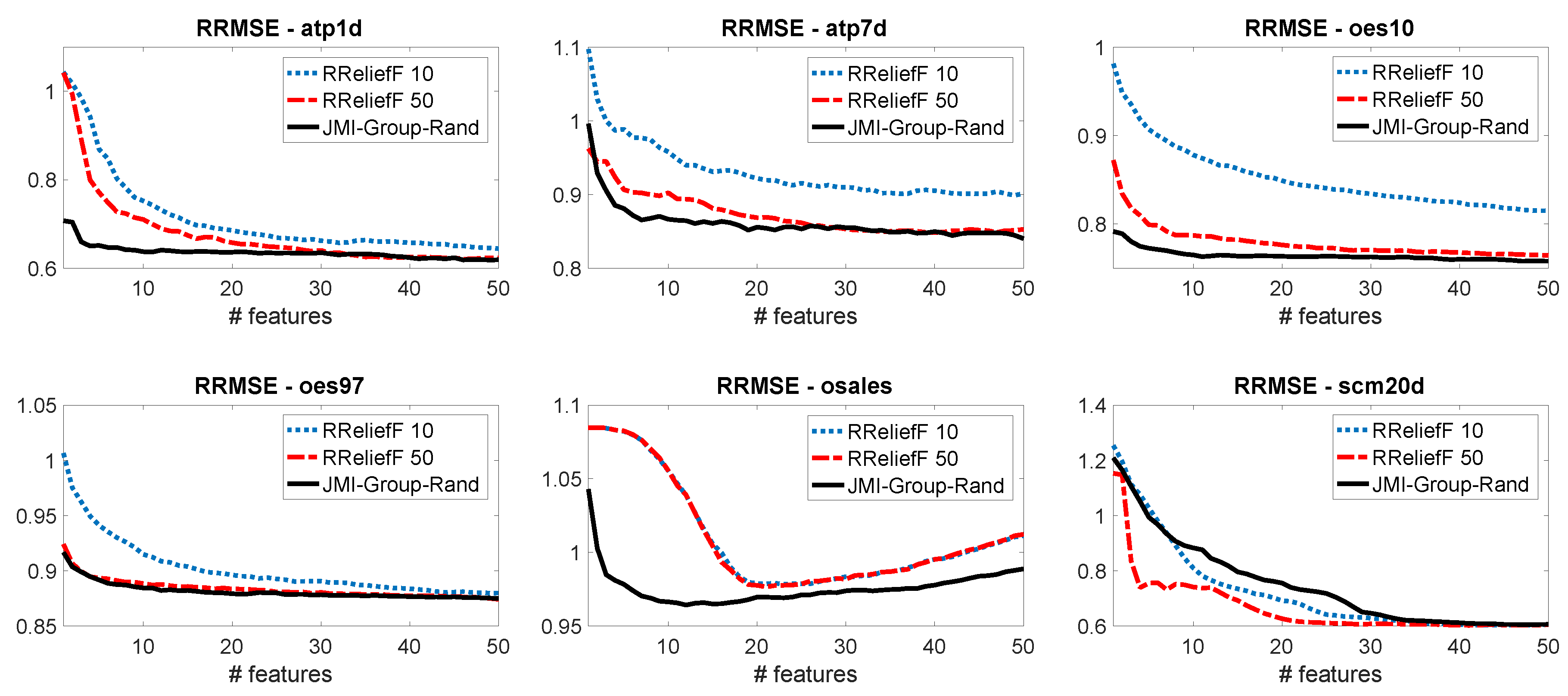
5. Experiments with Multivariate Regression Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FS | Feature Selection |
| MI | Mutual Information |
| CMI | Conditional Mutual Information |
| JMI | Joint Mutual Information |
| NoC | Number of Clusters |
| PoT | Proportion of Targets |
References
- Guyon, I.M.; Gunn, S.R.; Nikravesh, M.; Zadeh, L. (Eds.) Feature Extraction: Foundations and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Waegeman, W.; Dembczynski, K.; Huellermeier, E. Multi-target prediction: A unifying view on problems and methods. arXiv 2018, arXiv:1809.02352. [Google Scholar] [CrossRef]
- Boutell, M.R.; Luo, J.; Shen, X.; Brown, C.M. Learning multi-label scene classification. Pattern Recognit. 2004, 37, 1757–1771. [Google Scholar] [CrossRef]
- Elisseeff, A.; Weston, J. A Kernel Method for Multi-Labelled Classification. In Advances in Neural Information Processing Systems (NIPS) 14; MIT Press: Cambridge, MA, USA, 2001; pp. 681–687. [Google Scholar]
- Kocev, D.; Džeroski, S.; White, M.D.; Newell, G.R.; Griffioen, P. Using single-and multi-target regression trees and ensembles to model a compound index of vegetation condition. Ecol. Model. 2009, 220, 1159–1168. [Google Scholar] [CrossRef]
- Sechidis, K.; Nikolaou, N.; Brown, G. Information Theoretic Feature Selection in Multi-label Data through Composite Likelihood. In S+SSPR 2014; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Brown, G.; Pocock, A.; Zhao, M.J.; Lujan, M. Conditional Likelihood Maximisation: A Unifying Framework for Information Theoretic Feature Selection. J. Mach. Learn. Res. (JMLR) 2012, 13, 27–66. [Google Scholar]
- Sechidis, K.; Spyromitros-Xioufis, E.; Vlahavas, I. Multi-target feature selection through output space clustering. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN), Bruges, Belgium, 24–26 April 2019. [Google Scholar]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Mining multi-label data. In Data Mining and Knowledge Discovery Handbook; Springer: Boston, MA, USA, 2009; pp. 667–685. [Google Scholar]
- Spolaôr, N.; Monard, M.C.; Tsoumakas, G.; Lee, H.D. A systematic review of multi-label feature selection and a new method based on label construction. Neurocomputing 2016, 180, 3–15. [Google Scholar] [CrossRef]
- Yang, Y.; Pedersen, J.O. A Comparative Study on Feature Selection in Text Categorization. In Proceedings of the 14th International Conference on Machine Learning (ICML), Nashville, TN, USA, 8–12 July 1997; pp. 412–420. [Google Scholar]
- Lee, J.; Lim, H.; Kim, D.W. Approximating mutual information for multi-label feature selection. Electron. Lett. 2012, 48, 929–930. [Google Scholar] [CrossRef]
- Chen, W.; Yan, J.; Zhang, B.; Chen, Z.; Yang, Q. Document transformation for multi-label feature selection in text categorization. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; pp. 451–456. [Google Scholar]
- Sechidis, K.; Sperrin, M.; Petherick, E.S.; Luján, M.; Brown, G. Dealing with under-reported variables: An information theoretic solution. Int. J. Approx. Reason. 2017, 85, 159–177. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.W. Feature selection for multi-label classification using multivariate mutual information. Pattern Recognit. Lett. 2013, 34, 349–357. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.W. Fast multi-label feature selection based on information-theoretic feature ranking. Pattern Recognit. 2015, 48, 2761–2771. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.W. SCLS: Multi-label Feature Selection based on Scalable Criterion for Large Label Set. Pattern Recognit. 2017, 66, 342–352. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Katakis, I.; Vlahavas, I. Random k-labelsets for multilabel classification. IEEE Trans. Knowl. Data Eng. 2011, 23, 1079–1089. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Brillinger, D.R. Some data analyses using mutual information. Braz. J. Probab. Stat. 2004, 18, 163–182. [Google Scholar]
- Tsoumakas, G.; Spyromitros-Xioufis, E.; Vilcek, J.; Vlahavas, I. Mulan: A Java Library for Multi-Label Learning. J. Mach. Learn. Res. 2011, 12, 2411–2414. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. A k-nearest neighbor based algorithm for multi-label classification. In Proceedings of the IEEE International Conference on Granular Computing, Beijing, China, 25–27 July 2005; Volume 2, pp. 718–721. [Google Scholar]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Fernandez-Lozano, C.; Gestal, M.; Munteanu, C.R.; Dorado, J.; Pazos, A. A methodology for the design of experiments in computational intelligence with multiple regression models. PeerJ 2016, 4, e2721. [Google Scholar] [CrossRef]
- Spyromitros-Xioufis, E.; Tsoumakas, G.; Groves, W.; Vlahavas, I. Multi-target regression via input space expansion: Treating targets as inputs. Mach. Learn. 2016, 104, 55–98. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Sechidis, K.; Brown, G. Simple strategies for semi-supervised feature selection. Mach. Learn. 2018, 107, 357–395. [Google Scholar] [CrossRef]
- Sechidis, K.; Papangelou, K.; Metcalfe, P.D.; Svensson, D.; Weatherall, J.; Brown, G. Distinguishing prognostic and predictive biomarkers: An information theoretic approach. Bioinformatics 2018, 34, 3365–3376. [Google Scholar] [CrossRef] [PubMed]

| Name | Application | Examples | Features | Labels | Distinct Labelsets |
|---|---|---|---|---|---|
| CAL500 | Music | 502 | 68 | 174 | 502 |
| emotions | Music | 593 | 72 | 6 | 27 |
| enron | Text | 1702 | 1001 | 53 | 752 |
| genbase | Biology | 662 | 1186 | 27 | 32 |
| image | Images | 2000 | 294 | 5 | 20 |
| languagelog | Text | 1460 | 1004 | 75 | 1241 |
| medical | Text | 978 | 1449 | 45 | 94 |
| scene | Images | 2407 | 294 | 6 | 15 |
| yeast | Bioinformatics | 2417 | 103 | 14 | 198 |
| (a) Hamming Loss | |||
| Single-JMI | Joint-JMI | Group-JMI-Rand | |
| (Our Method) | |||
| CAL500 | 2.05 | 2.10 | 1.85 |
| emotions | 2.33 | 1.85 | 1.82 |
| enron | 2.10 | 1.00 | 2.90 |
| genbase | 2.11 | 1.71 | 2.17 |
| image | 1.90 | 2.73 | 1.38 |
| medical | 2.01 | 2.86 | 1.12 |
| scene | 1.80 | 1.25 | 2.95 |
| yeast | 1.57 | 3.00 | 1.43 |
| languagelog | 1.60 | 1.40 | 3.00 |
| Total wins | 0 | 4 | 5 |
| (b) Ranking Loss | |||
| Single-JMI | Joint-JMI | Group-JMI-Rand | |
| (Our Method) | |||
| CAL500 | 2.20 | 1.93 | 1.88 |
| emotions | 1.57 | 2.40 | 2.02 |
| enron | 1.75 | 1.30 | 2.95 |
| genbase | 2.29 | 1.66 | 2.05 |
| image | 1.90 | 2.77 | 1.32 |
| medical | 2.11 | 2.79 | 1.10 |
| scene | 1.90 | 1.15 | 2.95 |
| yeast | 1.52 | 3.00 | 1.48 |
| languagelog | 2.62 | 2.38 | 1.00 |
| Total wins | 1 | 3 | 5 |
| (c) Normalised Coverage | |||
| Single-JMI | Joint-JMI | Group-JMI-Rand | |
| (Our Method) | |||
| CAL500 | 1.75 | 2.35 | 1.90 |
| emotions | 1.95 | 2.80 | 1.25 |
| enron | 1.82 | 1.25 | 2.92 |
| genbase | 2.14 | 1.44 | 2.42 |
| image | 2.08 | 2.50 | 1.43 |
| languagelog | 2.40 | 2.60 | 1.00 |
| medical | 1.96 | 2.84 | 1.20 |
| scene | 1.57 | 1.48 | 2.95 |
| yeast | 1.62 | 3.00 | 1.38 |
| Total wins | 1 | 3 | 5 |
| (d) Macro-average F-measure | |||
| Single-JMI | Joint-JMI | Group-JMI-Rand | |
| (Our Method) | |||
| CAL500 | 1.92 | 2.25 | 1.82 |
| emotions | 2.10 | 2.08 | 1.82 |
| enron | 2.00 | 1.00 | 3.00 |
| genbase | 2.34 | 1.49 | 2.17 |
| image | 1.77 | 2.80 | 1.43 |
| languagelog | 1.43 | 1.65 | 2.92 |
| medical | 2.01 | 2.84 | 1.15 |
| scene | 1.77 | 1.30 | 2.92 |
| yeast | 1.75 | 3.00 | 1.25 |
| Total wins | 1 | 3 | 5 |
| Name | Application | Examples | Features | Targets |
|---|---|---|---|---|
| atp1d | Airline Ticket Price | 337 | 411 | 6 |
| atp7d | Airline Ticket Price | 296 | 411 | 6 |
| oes97 | Occupational Employment Survey | 334 | 263 | 16 |
| oes10 | Occupational Employment Survey | 403 | 298 | 16 |
| osales | Online Product Sales | 639 | 413 | 12 |
| scm20d | Supply Chain Management | 8966 | 61 | 16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sechidis, K.; Spyromitros-Xioufis, E.; Vlahavas, I. Information Theoretic Multi-Target Feature Selection via Output Space Quantization. Entropy 2019, 21, 855. https://doi.org/10.3390/e21090855
Sechidis K, Spyromitros-Xioufis E, Vlahavas I. Information Theoretic Multi-Target Feature Selection via Output Space Quantization. Entropy. 2019; 21(9):855. https://doi.org/10.3390/e21090855
Chicago/Turabian StyleSechidis, Konstantinos, Eleftherios Spyromitros-Xioufis, and Ioannis Vlahavas. 2019. "Information Theoretic Multi-Target Feature Selection via Output Space Quantization" Entropy 21, no. 9: 855. https://doi.org/10.3390/e21090855
APA StyleSechidis, K., Spyromitros-Xioufis, E., & Vlahavas, I. (2019). Information Theoretic Multi-Target Feature Selection via Output Space Quantization. Entropy, 21(9), 855. https://doi.org/10.3390/e21090855





