Multivariate Multiscale Dispersion Entropy of Biomedical Times Series
Abstract
:1. Introduction
2. Multivariate Multiscale Dispersion Entropy (mvMDE)
2.1. Coarse-Graining Process for Multivariate Signals
2.2. Background Information for the mvDE
2.2.1. mvDEI
2.2.2. mvDEII
2.2.3. mvDEIII
2.3. Multivariate Dispersion Entropy (mvDE)
2.4. Parameters of the mvMDE, mvMSE, and mvMFE Methods
3. Evaluation Signals
3.1. Synthetic Signals
3.2. Real Biomedical Datasets
4. Results and Discussions
4.1. Synthetic Signals
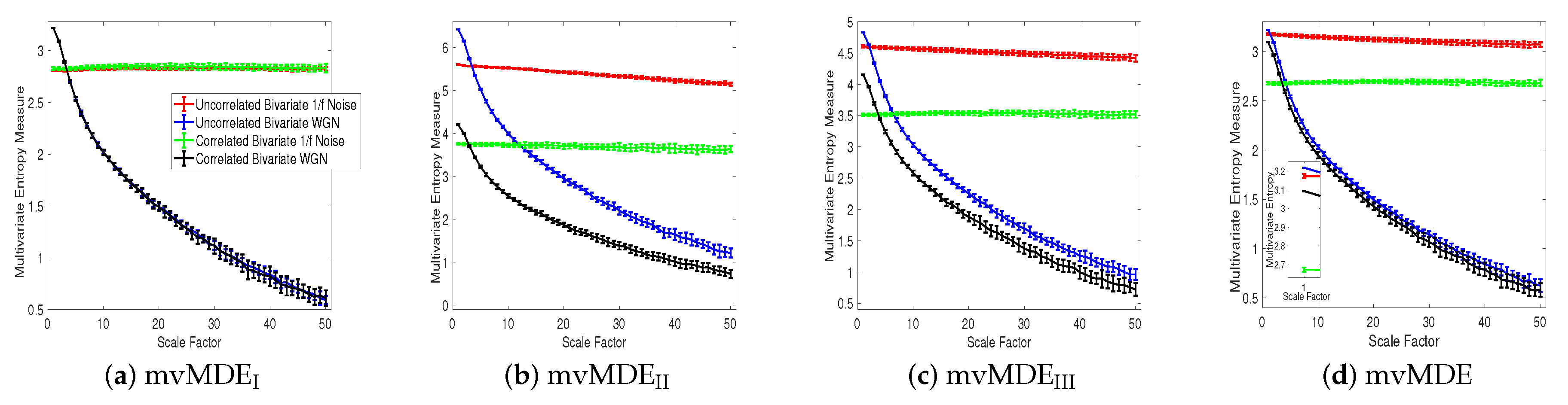
4.1.1. Uncorrelated White Gaussian and Noises
4.1.2. Computational Time
4.1.3. Correlated white Gaussian and Noises
4.1.4. Bivariate AR Processes
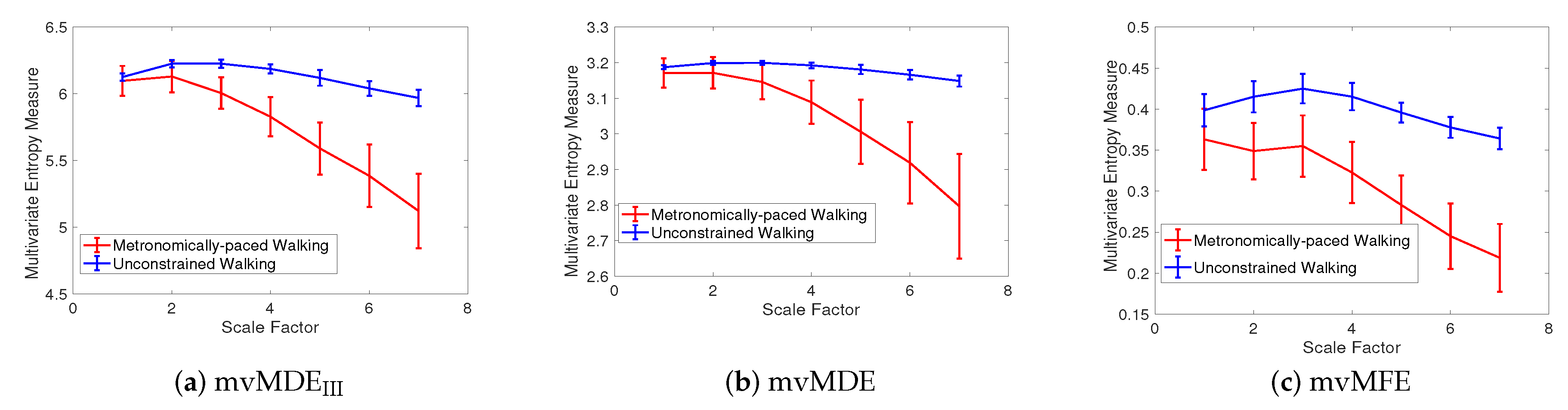
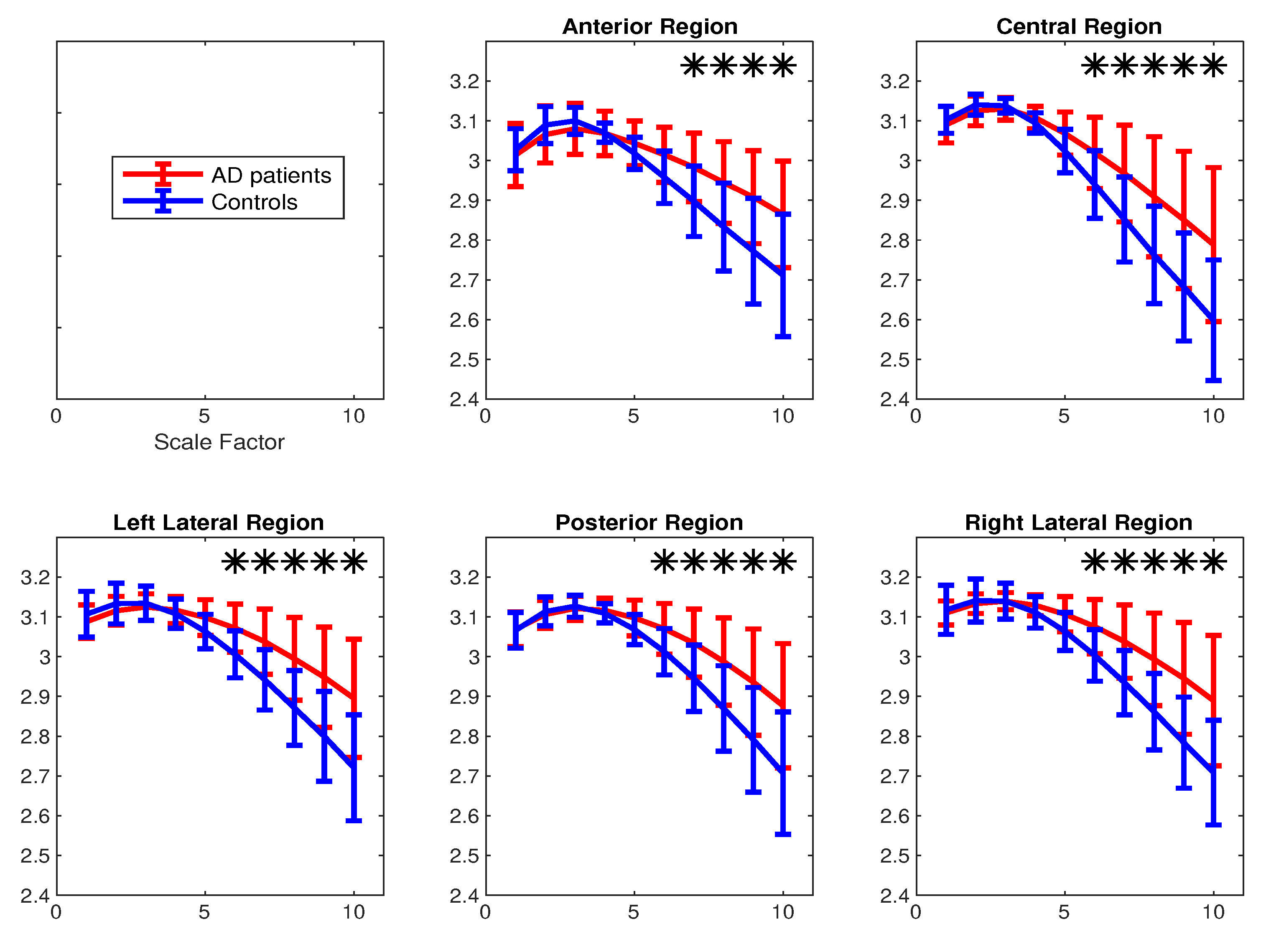
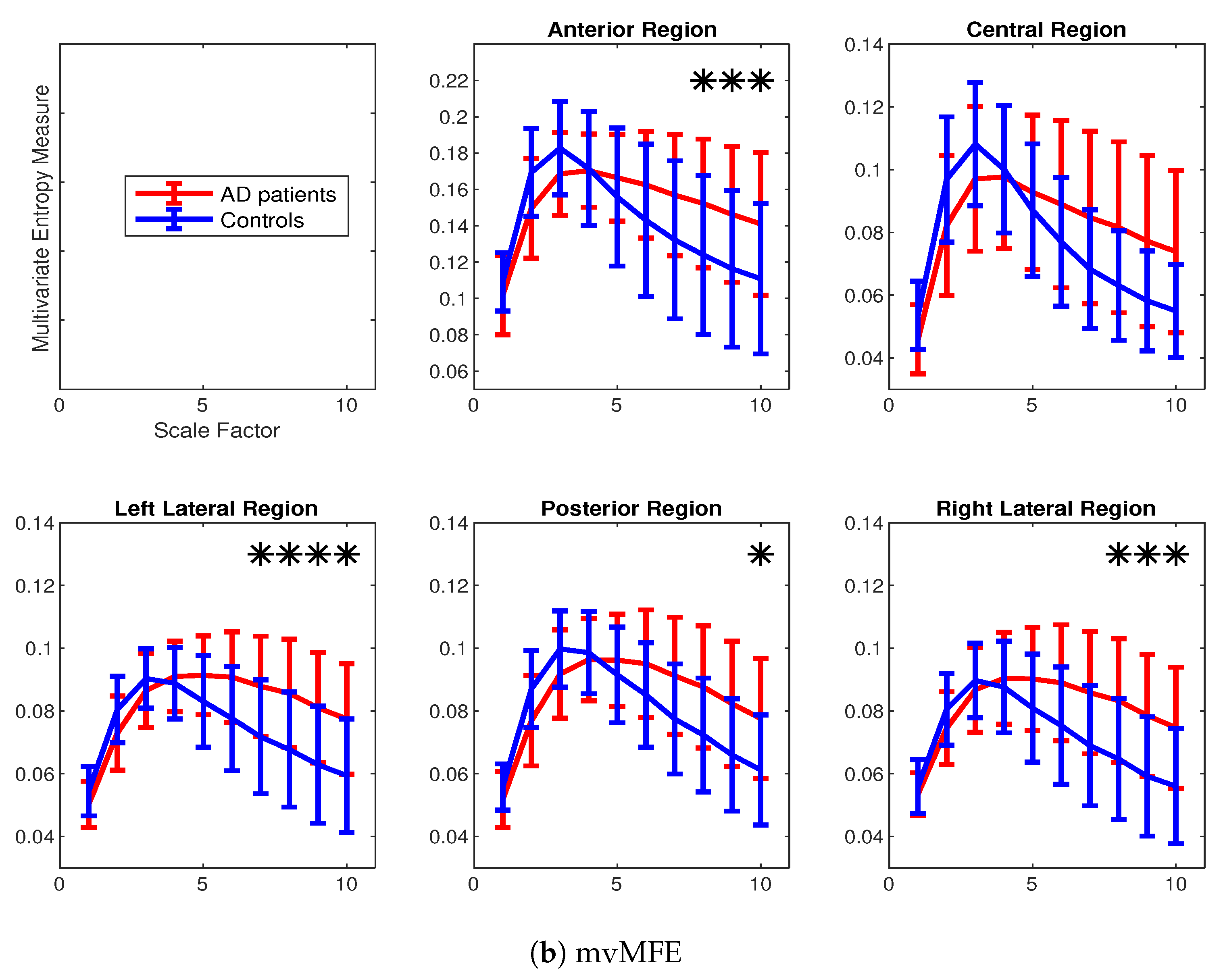
4.2. Real Biomedical Datasets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cerutti, S.; Hoyer, D.; Voss, A. Multiscale, multiorgan and multivariate complexity analyses of cardiovascular regulation. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2009, 367, 1337–1358. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Rehman, N.; Looney, D.; Rutkowski, T.; Mandic, D. Dynamical complexity of human responses: A multivariate data-adaptive framework. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 433–445. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Cerutti, S. Multivariate and multiscale analysis of biomedical signals: Towards a comprehensive approach to medical diagnosis. In Proceedings of the 2012 25th International Symposium on Computer-Based Medical Systems (CBMS), Rome, Italy, 20–22 June 2012; pp. 1–5. [Google Scholar]
- Fernández-Sotos, A.; Martínez-Rodrigo, A.; Moncho-Bogani, J.; Latorre, J.M.; Fernández-Caballero, A. Neural Correlates of Phrase Quadrature Perception in Harmonic Rhythm: An Eeg Study (Using a Brain-Computer Interface). Int. J. Neural Syst. 2018, 28, 1750054. [Google Scholar] [CrossRef] [PubMed]
- Spyrou, L.; Martín-Lopez, D.; Valentín, A.; Alarcón, G.; Sanei, S. Detection of intracranial signatures of interictal epileptiform discharges from concurrent scalp EEG. Int. J. Neural Syst. 2016, 26, 1650016. [Google Scholar] [CrossRef] [PubMed]
- Pereda, E.; Quiroga, R.Q.; Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005, 77, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [Green Version]
- Mammone, N.; Bonanno, L.; Salvo, S.D.; Marino, S.; Bramanti, P.; Bramanti, A.; Morabito, F.C. Permutation disalignment index as an indirect, EEG-based, measure of brain connectivity in MCI and AD patients. Int. J. Neural Syst. 2017, 27, 1750020. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [Green Version]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Fogedby, H.C. On the phase space approach to complexity. J. Stat. Phys. 1992, 69, 411–425. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Cabella, B.C.T.; da Costa Neves, U.P.; Junior, L.O.M. Multiscale entropy-based methods for heart rate variability complexity analysis. Phys. A Stat. Mech. Its Appl. 2015, 422, 143–152. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Phys. A Stat. Mech. Its Appl. 2017, 465, 261–276. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Ji, L.; Yan, C.; Li, K.; Liu, C.; Liu, C. Coupling between short-term heart rate and diastolic period is reduced in heart failure patients as indicated by multivariate entropy analysis. In Proceedings of the Computing in Cardiology Conference (CinC), Cambridge, MA, USA, 7–10 September 2014; pp. 97–100. [Google Scholar]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P. Multivariate weighted multiscale permutation entropy for complex time series. Nonlinear Dyn. 2017, 88, 1707–1722. [Google Scholar] [CrossRef]
- Azami, H.; Abásolo, D.; Simons, S.; Escudero, J. Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s Disease. Entropy 2017, 19, 31. [Google Scholar] [CrossRef]
- Labate, D.; La Foresta, F.; Morabito, G.; Palamara, I.; Morabito, F.C. Entropic measures of EEG complexity in alzheimer’s disease through a multivariate multiscale approach. Sens. J. 2013, 13, 3284–3292. [Google Scholar] [CrossRef]
- Gao, Z.K.; Ding, M.S.; Geng, H.; Jin, N.D. Multivariate multiscale entropy analysis of horizontal oil–Water two-phase flow. Phys. A Stat. Mech. Its Appl. 2015, 417, 7–17. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D.H.; Wang, K.H.; Liu, Q.; Abbod, M.F.; Jiang, B.C.; Chen, K.P.; Wu, C.; Shieh, J.S. Multivariate multiscale entropy applied to center of pressure signals analysis: An effect of vibration stimulation of shoes. Entropy 2012, 14, 2157–2172. [Google Scholar] [CrossRef]
- Zhao, L.; Wei, S.; Tang, H.; Liu, C. Multivariable Fuzzy Measure Entropy Analysis for Heart Rate Variability and Heart Sound Amplitude Variability. Entropy 2016, 18, 430. [Google Scholar] [CrossRef]
- Ramdani, S.; Bonnet, V.; Tallon, G.; Lagarde, J.; Bernard, P.L.; Blain, H. Parameters Selection for Bivariate Multiscale Entropy Analysis of Postural Fluctuations in Fallers and Non-Fallers Older Adults. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 859–871. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Rostaghi, M.; Abasolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar] [PubMed] [Green Version]
- Azami, H.; Escudero, J. Coarse-Graining Approaches in Univariate Multiscale Sample and Dispersion Entropy. Entropy 2018, 20, 138. [Google Scholar] [CrossRef]
- Azami, H.; Kinney-lang, E.; Ebied, A.; Fernández, A.; Escudero, J. Multiscale dispersion entropy for the regional analysis of resting-state magnetoencephalogram complexity in Alzheimer’s disease. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 3182–3185. [Google Scholar]
- Azami, H.; Escudero, J. Amplitude-and Fluctuation-Based Dispersion Entropy. Entropy 2018, 20, 210. [Google Scholar] [CrossRef]
- Tufféry, S. Data Mining and Statistics for Decision Making; Wiley: Chichester, UK, 2011; Volume 2. [Google Scholar]
- Baranwal, G.; Vidyarthi, D.P. Admission control in cloud computing using game theory. J. Supercomput. 2016, 72, 317–346. [Google Scholar] [CrossRef]
- Gibbs, M.N.; MacKay, D.J. Variational Gaussian process classifiers. IEEE Trans. Neural Netw. 2000, 11, 1458–1464. [Google Scholar] [Green Version]
- Duch, W. Uncertainty of data, fuzzy membership functions, and multilayer perceptrons. IEEE Trans. Neural Netw. 2005, 16, 10–23. [Google Scholar] [CrossRef]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Phys. D Nonlinear Phenom. 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A. The effect of time delay on approximate & sample entropy calculations. Phys. D Nonlinear Phenom. 2008, 237, 3069–3074. [Google Scholar]
- Humeau-Heurtier, A. Multivariate generalized multiscale entropy analysis. Entropy 2016, 18, 411. [Google Scholar] [CrossRef]
- Penny, W.; Roberts, S. Bayesian multivariate autoregressive models with structured priors. IEE Proc. Vis. Image Signal Process. 2002, 149, 33–41. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Purdon, P.L.; Peng, C.; Ladin, Z.; Wei, J.Y.; Goldberger, A.L. Fractal dynamics of human gait: Stability of long-range correlations in stride interval fluctuations. J. Appl. Physiol. 1996, 80, 1448–1457. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Schindler, K.; Rummel, C. Nonrandomness, nonlinear dependence, and nonstationarity of electroencephalographic recordings from epilepsy patients. Phys. Rev. E 2012, 86, 046206. [Google Scholar] [CrossRef] [Green Version]
- Escudero, J.; Sanei, S.; Jarchi, D.; Abásolo, D.; Hornero, R. Regional coherence evaluation in mild cognitive impairment and Alzheimer’s disease based on adaptively extracted magnetoencephalogram rhythms. Physiol. Meas. 2011, 32, 1163. [Google Scholar] [CrossRef]
- Lake, D.E.; Moorman, J.R. Accurate estimation of entropy in very short physiological time series: The problem of atrial fibrillation detection in implanted ventricular devices. Am. J. Physiol. Heart Circ. Physiol. 2010, 300, H319–H325. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Yang, A.C.; Wang, S.J.; Lai, K.L.; Tsai, C.F.; Yang, C.H.; Hwang, J.P.; Lo, M.T.; Huang, N.E.; Peng, C.K.; Fuh, J.L. Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer’s disease. Prog. Neuro Psychopharmacol. Biol. Psychiatry 2013, 47, 52–61. [Google Scholar] [CrossRef]
- Hornero, R.; Abásolo, D.; Escudero, J.; Gómez, C. Nonlinear analysis of electroencephalogram and magnetoencephalogram recordings in patients with Alzheimer’s disease. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2009, 367, 317–336. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, R.; Cooper, H.; Hedges, L. Parametric measures of effect size. Handb. Res. Synth. 1994, 621, 231–244. [Google Scholar]
- Sullivan, G.M.; Feinn, R. Using effect size—Or why the P value is not enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Liang, H. Adaptive multiscale entropy analysis of multivariate neural data. IEEE Trans. Biomed. Eng. 2012, 59, 12–15. [Google Scholar]
- Hu, M.; Liang, H. Perceptual suppression revealed by adaptive multi-scale entropy analysis of local field potential in monkey visual cortex. Int. J. Neural Syst. 2013, 23, 1350005. [Google Scholar] [CrossRef] [PubMed]
- Tonoyan, Y.; Looney, D.; Mandic, D.P.; Van Hulle, M.M. Discriminating multiple emotional states from EEG using a data-adaptive, multiscale information-theoretic approach. Int. J. Neural Syst. 2016, 26, 1650005. [Google Scholar] [CrossRef] [PubMed]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Renner, R.; Wolf, S. Smooth Rényi entropy and applications. In Proceedings of the International Symposium onInformation Theory (ISIT 2004), Chicago, IL, USA, 27 June–2 July 2004; p. 233. [Google Scholar]






| Methods | Spatial Domain | Short Signals | Typical Number of Elements Stored | Typical Number of Samples |
|---|---|---|---|---|
| mvSE [3] | yes | undefined | ||
| mvFE [17] | yes | unreliable | ||
| mvPE [19] and mvWPE [20] | no | reliable | ||
| mvDEI | no | reliable | ||
| mvDEII | yes | unreliable | ||
| mvDEIII | yes | unreliable | ||
| mvDE | yes | reliable |
| Time Series | mvMDEI | mvMDEII | mvMDEIII | mvMDE | mvMSE | mvMFE |
|---|---|---|---|---|---|---|
| All three channels contain noise | 0.0028 | 0.0025 | 0.0037 | 0.0022 | 0.0405 | 0.0355 |
| Two channels contain noise and one contains WGN | 0.0042 | 0.0032 | 0.0036 | 0.0044 | 0.0283 | 0.0274 |
| One channel contains noise and two contain WGN | 0.0066 | 0.0052 | 0.0058 | 0.0061 | 0.0305 | 0.0292 |
| All three channels contain WGN | 0.0072 | 0.0080 | 0.0092 | 0.0101 | 0.0232 | 0.0211 |
| Number of Channels and Samples | mvMSE | mvMFE | mvMDEI | mvMDEII | mvMDEIII | mvMDE |
|---|---|---|---|---|---|---|
| 2 channels and 1000 samples | 0.051 s | 0.066 s | 0.014 s | 0.023 s | 0.026 s | 0.020 s |
| 2 channels and 3000 samples | 0.237 s | 0.296 s | 0.035 s | 0.057 s | 0.068 s | 0.052 s |
| 2 channels and 10,000 samples | 1.821 s | 2.016 s | 0.111 s | 0.190 s | 0.223 s | 0.181 s |
| 5 channels and 1000 samples | 0.209 s | 0.223 s | 0.028 s | 43.096 s | 0.490 s | 0.050 s |
| 5 channels and 3000 samples | 1.129 s | 1.204 s | 0.080 s | 82.246 s | 1.137 s | 0.137 s |
| 5 channels and 10,000 samples | 9.432 s | 9.801 s | 0.260 s | 218.553 s | 3.343 s | 0.491 s |
| 8 channels and 1000 samples | 0.489 s | 0.501 s | 0.042 s | out of memory error | 65.560 s | 0.086 s |
| 8 channels and 3000 samples | 2.973 s | 2.906 s | 0.124 s | out of memory error | 150.122 s | 0.243 s |
| 8 channels and 10,000 samples | 27.993 s | 25.951 s | 0.398 s | out of memory error | 363.752 s | 0.824 s |
| Stride Interval Fluctuations | mvMFE | mvMDEIII | mvMDE |
|---|---|---|---|
| Self-paced walk | 0.040 | 0.005 | 0.002 |
| Metronomically-paced walk | 0.116 | 0.025 | 0.019 |
| Signals | mvMSE | mvMFE | mvMDEII | mvMDEIII | mvMDE |
|---|---|---|---|---|---|
| focal EEGs | 0.019 | 0.019 | 0.006 | 0.003 | 0.002 |
| Non-focal EEGs | 0.021 | 0.015 | 0.008 | 0.003 | 0.002 |
| Region-Method | Scale 1 | Scale 2 | Scale 3 | Scale 4 | Scale 5 | Scale 6 | Scale 7 | Scale 8 | Scale 9 | Scale 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Anterior-mvMFE | 0.36 | 0.73 | 0.57 | 0.04 | 0.33 | 0.53 | 0.63 | 0.70 | 0.72 | 0.73 |
| Central-mvMFE | 0.68 | 0.67 | 0.49 | 0.10 | 0.23 | 0.48 | 0.65 | 0.76 | 0.79 | 0.83 |
| Left lateral-mvMFE | 0.53 | 0.64 | 0.34 | 0.18 | 0.60 | 0.83 | 0.92 | 0.98 | 0.97 | 0.98 |
| Posterior-mvMFE | 0.46 | 0.72 | 0.58 | 0.16 | 0.30 | 0.57 | 0.73 | 0.78 | 0.82 | 0.85 |
| Right lateral-mvMFE | 0.30 | 0.50 | 0.22 | 0.18 | 0.53 | 0.71 | 0.84 | 0.92 | 0.97 | 0.95 |
| Anterior-mvMDE | 0.18 | 0.37 | 0.36 | 0.03 | 0.49 | 0.80 | 0.95 | 1.02 | 1.06 | 1.04 |
| Central-mvMDE | 0.29 | 0.45 | 0.29 | 0.48 | 0.78 | 0.88 | 0.97 | 1.01 | 1.03 | 1.04 |
| Left lateral-mvMDE | 0.37 | 0.40 | 0.24 | 0.24 | 0.77 | 1.07 | 1.17 | 1.20 | 1.19 | 1.19 |
| Posterior-mvMDE | 0.05 | 0.19 | 0.18 | 0.24 | 0.67 | 0.90 | 1.015 | 1.05 | 1.06 | 1.06 |
| Right lateral-mvMDE | 0.15 | 0.19 | 0.00 | 0.51 | 0.90 | 1.05 | 1.14 | 1.18 | 1.20 | 1.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azami, H.; Fernández, A.; Escudero, J. Multivariate Multiscale Dispersion Entropy of Biomedical Times Series. Entropy 2019, 21, 913. https://doi.org/10.3390/e21090913
Azami H, Fernández A, Escudero J. Multivariate Multiscale Dispersion Entropy of Biomedical Times Series. Entropy. 2019; 21(9):913. https://doi.org/10.3390/e21090913
Chicago/Turabian StyleAzami, Hamed, Alberto Fernández, and Javier Escudero. 2019. "Multivariate Multiscale Dispersion Entropy of Biomedical Times Series" Entropy 21, no. 9: 913. https://doi.org/10.3390/e21090913
APA StyleAzami, H., Fernández, A., & Escudero, J. (2019). Multivariate Multiscale Dispersion Entropy of Biomedical Times Series. Entropy, 21(9), 913. https://doi.org/10.3390/e21090913






