Fractional Refined Composite Multiscale Fuzzy Entropy of International Stock Indices
Abstract
:1. Introduction
2. Methodologies
2.1. Fuzzy Entropy
2.2. Fractional Refined Composite Multiscale Fuzzy Entropy
3. Complexity Measure for Synthetic Data
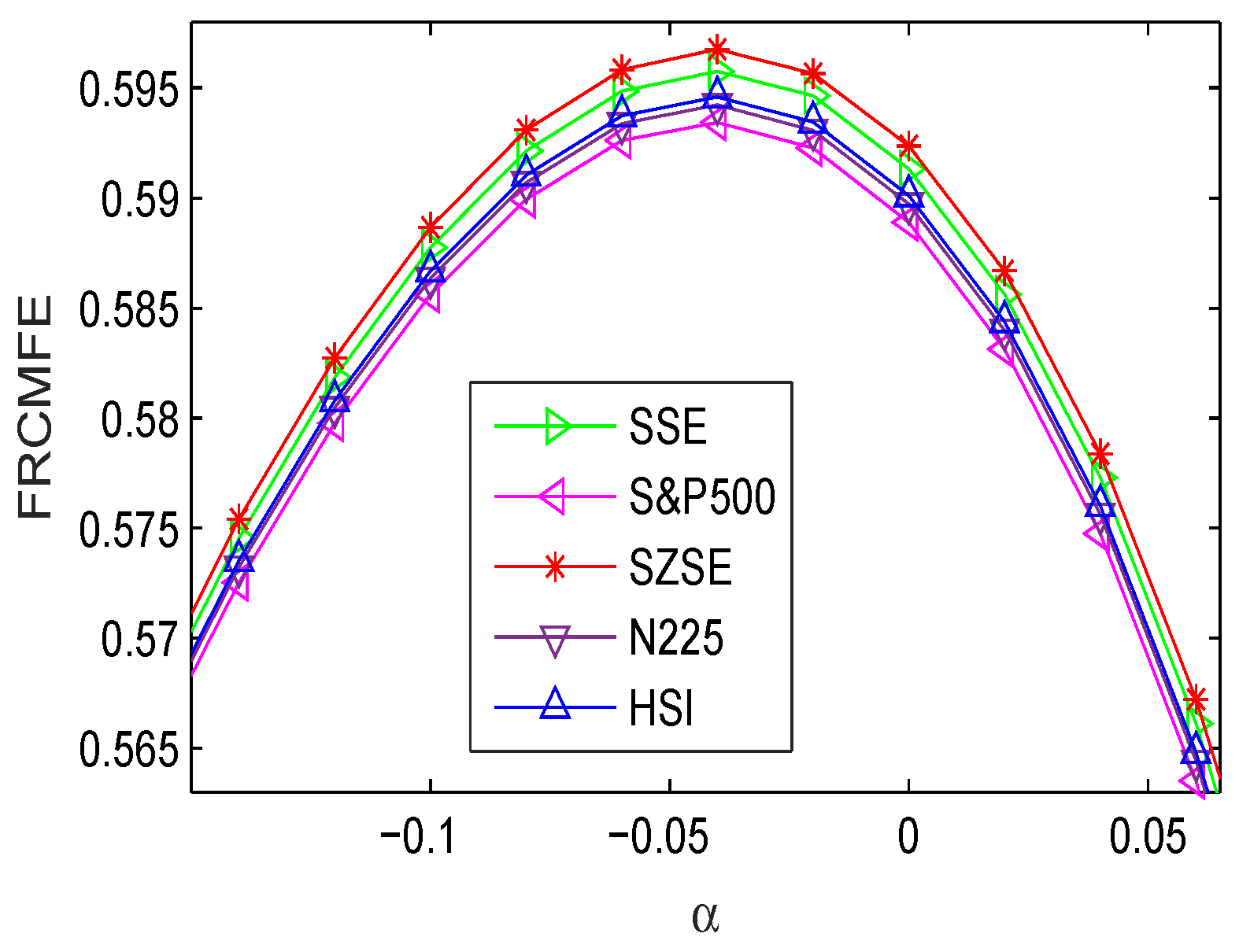
4. Complexity Measure for International Stock Indices
4.1. Complexity Measure of Returns
4.2. Complexity Measure of Volatility
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FRCMFE | Fractional refined composite multiscale fuzzy entropy |
| FuzzyEn | Fuzzy entropy |
| CMFE | Composite multiscale fuzzy entropy |
| RCMFE | Refined composite multiscale fuzzy entropy |
| MFE | Multiscale fuzzy entropy |
References
- Calvet, L.; Fisher, A. Multifractal Volatility: Theory, Forecasting, and Pricing; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Chen, W.C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fract. 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
- Machado, J.T. Complex dynamics of financial indices. Nonlinear Dyn. 2013, 74, 287–296. [Google Scholar] [CrossRef] [Green Version]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Financ. 2001, 1, 223–236. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. An Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ilinski, K. Physics of Finance, Gauge Modeling in Nonequilibrium Pricing; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Mills, T.C. The Econometric Modeling of Financial Time Series; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Chen, W.T.; Zhuang, J.; Yu, W.X.; Wang, Z.Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2007, 89, 705–708. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Niu, H.L.; Wang, J. Quantifying complexity of financial short-term time series by composite multiscale entropy measure. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 375–382. [Google Scholar] [CrossRef]
- João, M.S.; Hernâni, G.; João, B.; Luís, A.; Mohammad, N.; Cristina, C.S. Entropy and Compression Capture Different Complexity Features: The Case of Fetal Heart Rate. Entropy 2017, 19, 688. [Google Scholar] [Green Version]
- Zhang, W.; Wang, J. Nonlinear stochastic exclusion financial dynamics modeling and complexity behaviors. Nonlinear Dyn. 2017, 88, 921–935. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Complexity Analysis of Global Temperature Time Series. Entropy 2018, 20, 437. [Google Scholar] [CrossRef]
- Antão, R.; Mota, A.; Machado, J.T. Kolmogorov complexity as a data similarity metric: Application in mitochondrial DNA. Nonlinear Dyn. 2018, 93, 1059–1071. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S.; Liu, B. On Nonlinear Complexity and Shannonś Entropy of Finite Length Random Sequences. Entropy 2015, 17, 1936–1945. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, F.; Gao, J.; Cheng, C.; Song, C. Characterizing Complexity Changes in Chinese Stock Markets by Permutation Entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Phys. A 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Chen, W.T.; Wang, Z.Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zheng, S.; Zhang, W.; Wang, J.; Wang, G. Modeling and complexity of stochastic interacting Lévy type financial price dynamics. Phys. A 2018, 499, 498–511. [Google Scholar] [CrossRef]
- Fouda, J.S.A.E.; Koepf, W.; Jacquir, S. The ordinal Kolmogorov-Sinai entropy: A generalized approximation. Commun. Nonlinear Sci. Numer. Simul. 2017, 46, 103–115. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A.; Wu, C.W.; Wu, S.D. Refined composite multiscale permutation entropy to overcome multiscale permutation entropy length dependence. IEEE Signal Proc. Lett. 2015, 22, 2364–2367. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J. Nonlinear stochastic interacting dynamics and complexity of financial gasket fractal-like lattice percolation. Phys. Lett. A 2018, 382, 1218–1225. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, S.; Zhang, W.; Wang, G.; Wang, J. Fuzzy entropy complexity and multifractal behavior of financial dynamics. Phys. A 2018, 506, 486–498. [Google Scholar] [CrossRef]
- Li, Y.; Miao, B.; Zhang, W.; Peng, C.; Liu, J.; Jiang, X. Refined composite multiscale fuzzy entropy: Localized defect detection of rolling element bearing. J. Mech. Sci. Technol. 2019, 33, 109–120. [Google Scholar] [CrossRef]
- Yin, J.; Su, C.; Zhang, Y.; Fan, X.H. Complexity Analysis of Carbon Market Using the Modified Multi-Scale Entropy. Entropy 2018, 20, 434. [Google Scholar] [CrossRef]
- María, M.G. Ordinal Patterns in Heartbeat Time Series: An Approach Using Multiscale Analysis. Entropy 2019, 21, 583. [Google Scholar] [Green Version]
- Machado, J.T.; Lopes, A.M. Fractional Jensen–Shannon analysis of the scientific output of researchers in fractional calculus. Entropy 2017, 19, 127. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. Fractional Rényi entropy. Eur. Phys. J. Plus 2019, 134, 217. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. Artistic painting: A fractional calculus perspective. Appl. Math. Model. 2019, 65, 614–626. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence; Springer: New York, NY, USA, 1981. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982. [Google Scholar]
- Machado, J.T. Fractional order generalized information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]




| Method | Data Length | ||||||
|---|---|---|---|---|---|---|---|
| 1000 | 1500 | 2000 | 2500 | 3000 | 5000 | 10,000 | |
| MFE ( = 10) | 0.0827 | 0.0794 | 0.0672 | 0.0483 | 0.0470 | 0.0339 | 0.0302 |
| CMFE ( = 10) | 0.0706 | 0.0538 | 0.0449 | 0.0378 | 0.0331 | 0.0313 | 0.0185 |
| RCMFE ( = 10) | 0.0684 | 0.0509 | 0.0466 | 0.0366 | 0.0327 | 0.0283 | 0.0180 |
| MFE ( = 20) | 0.0885 | 0.0823 | 0.0788 | 0.0663 | 0.0717 | 0.0498 | 0.0337 |
| CMFE ( = 20) | 0.0763 | 0.0681 | 0.0568 | 0.0544 | 0.0397 | 0.0340 | 0.0290 |
| RCMFE ( = 20) | 0.0716 | 0.0658 | 0.0517 | 0.0397 | 0.0393 | 0.0337 | 0.0228 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| 1 | 0.9329 | 0.8888 | 0.9533 | 1.0754 | 0.9673 |
| 3 | 0.5968 | 0.5235 | 0.6029 | 0.6736 | 0.6139 |
| 5 | 0.4574 | 0.3833 | 0.4637 | 0.5034 | 0.4672 |
| 7 | 0.4049 | 0.3077 | 0.4059 | 0.4016 | 0.3750 |
| 9 | 0.3427 | 0.2518 | 0.3411 | 0.3417 | 0.3352 |
| 12 | 0.3032 | 0.2127 | 0.3050 | 0.2948 | 0.2836 |
| 16 | 0.2576 | 0.1771 | 0.2621 | 0.2317 | 0.2371 |
| 20 | 0.2346 | 0.1635 | 0.2493 | 0.2099 | 0.2131 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| 1 | 0.9329 | 0.8888 | 0.9533 | 1.0754 | 0.9673 |
| 3 | 0.6022 | 0.5263 | 0.6134 | 0.6550 | 0.6108 |
| 5 | 0.4715 | 0.3948 | 0.4824 | 0.5058 | 0.4709 |
| 7 | 0.3965 | 0.3154 | 0.4017 | 0.4070 | 0.3846 |
| 9 | 0.3414 | 0.2637 | 0.3517 | 0.3418 | 0.3272 |
| 12 | 0.2984 | 0.2116 | 0.3053 | 0.2826 | 0.2773 |
| 16 | 0.2615 | 0.1765 | 0.2722 | 0.2332 | 0.2381 |
| 20 | 0.2319 | 0.1492 | 0.2442 | 0.1975 | 0.2062 |
| SZSE | SSE | HSI | N225 | S&P500 | |
|---|---|---|---|---|---|
| 2 | 0.5990 | 0.5972 | 0.5960 | 0.5957 | 0.5943 |
| 3 | 0.5962 | 0.5951 | 0.5939 | 0.5942 | 0.5927 |
| 4 | 0.5948 | 0.5939 | 0.5934 | 0.5935 | 0.5927 |
| 5 | 0.5945 | 0.5939 | 0.5931 | 0.5930 | 0.5924 |
| 6 | 0.5942 | 0.5935 | 0.5929 | 0.5927 | 0.5920 |
| 7 | 0.5937 | 0.5930 | 0.5926 | 0.5924 | 0.5920 |
| 8 | 0.5933 | 0.5928 | 0.5924 | 0.5923 | 0.5919 |
| 10 | 0.5930 | 0.5924 | 0.5924 | 0.5922 | 0.5918 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| −0.3 | 0.4811 | 0.4795 | 0.4817 | 0.4801 | 0.4803 |
| −0.2 | 0.5457 | 0.5439 | 0.5465 | 0.5445 | 0.5448 |
| −0.1 | 0.5877 | 0.5856 | 0.5887 | 0.5863 | 0.5867 |
| −0.04 | 0.5958 | 0.5934 | 0.5967 | 0.5942 | 0.5946 |
| 0 | 0.5913 | 0.5889 | 0.5924 | 0.5897 | 0.5901 |
| 0.1 | 0.5341 | 0.5314 | 0.5353 | 0.5323 | 0.5328 |
| 0.2 | 0.3822 | 0.3794 | 0.3854 | 0.3803 | 0.3808 |
| 0.3 | 0.0794 | 0.0767 | 0.0806 | 0.0776 | 0.0780 |
| 0.4 | −0.4777 | −0.4800 | −0.4767 | −0.4792 | −0.4788 |
| 0.5 | −1.5028 | −1.5038 | −1.5024 | −1.5034 | −1.5033 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| −0.3 | 0.4798 | 0.4789 | 0.4800 | 0.4793 | 0.4794 |
| −0.2 | 0.5442 | 0.5432 | 0.5444 | 0.5435 | 0.5437 |
| −0.1 | 0.5860 | 0.5848 | 0.5862 | 0.5852 | 0.5854 |
| −0.04 | 0.5938 | 0.5929 | 0.5941 | 0.5930 | 0.5933 |
| 0 | 0.5893 | 0.5879 | 0.5896 | 0.5884 | 0.5887 |
| 0.1 | 0.5319 | 0.5304 | 0.5322 | 0.5309 | 0.5312 |
| 0.2 | 0.3799 | 0.3783 | 0.3802 | 0.3788 | 0.3792 |
| 0.3 | 0.0771 | 0.0756 | 0.0775 | 0.0761 | 0.0764 |
| 0.4 | −0.4796 | −0.4809 | −0.4793 | −0.4804 | −0.4802 |
| 0.5 | −1.5036 | −1.5041 | −1.5035 | −1.5039 | −1.5038 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| 1 | 0.9614 | 0.7745 | 0.8403 | 0.7986 | 0.8148 |
| 3 | 0.6337 | 0.4977 | 0.4889 | 0.5158 | 0.5367 |
| 5 | 0.5148 | 0.4080 | 0.3897 | 0.4275 | 0.4427 |
| 7 | 0.4538 | 0.3826 | 0.3299 | 0.3783 | 0.3967 |
| 9 | 0.4301 | 0.3523 | 0.3021 | 0.3633 | 0.3747 |
| 12 | 0.4057 | 0.3409 | 0.2895 | 0.3496 | 0.3539 |
| 16 | 0.3661 | 0.3314 | 0.22782 | 0.3505 | 0.3519 |
| 20 | 0.3909 | 0.3230 | 0.2785 | 0.3615 | 0.3433 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| 1 | 0.7986 | 0.7745 | 0.8148 | 0.9614 | 0.8403 |
| 3 | 0.5236 | 0.4868 | 0.5245 | 0.6238 | 0.4876 |
| 5 | 0.4284 | 0.3985 | 0.4418 | 0.5123 | 0.3783 |
| 7 | 0.3821 | 0.3668 | 0.3876 | 0.4522 | 0.3261 |
| 9 | 0.3631 | 0.3519 | 0.3684 | 0.3684 | 0.3056 |
| 12 | 0.3537 | 0.3410 | 0.3535 | 0.4037 | 0.2954 |
| 16 | 0.3494 | 0.3280 | 0.3437 | 0.3904 | 0.2851 |
| 20 | 0.3491 | 0.3197 | 0.3440 | 0.3868 | 0.2791 |
| SSE | S&P500 | SZSE | N225 | HSI | |
|---|---|---|---|---|---|
| 2 | 0.5328 | 0.5311 | 0.5335 | 0.5318 | 0.5317 |
| 3 | 0.5316 | 0.5306 | 0.5321 | 0.5312 | 0.5310 |
| 4 | 0.5313 | 0.5305 | 0.5316 | 0.5309 | 0.5308 |
| 5 | 0.5310 | 0.5304 | 0.5314 | 0.5308 | 0.5307 |
| 6 | 0.5308 | 0.5303 | 0.5312 | 0.5306 | 0.5305 |
| 7 | 0.5308 | 0.5303 | 0.5311 | 0.5306 | 0.5305 |
| 8 | 0.5307 | 0.5303 | 0.5309 | 0.5306 | 0.5305 |
| 10 | 0.5306 | 0.5302 | 0.5308 | 0.5305 | 0.5308 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Zhang, W. Fractional Refined Composite Multiscale Fuzzy Entropy of International Stock Indices. Entropy 2019, 21, 914. https://doi.org/10.3390/e21090914
Wu Z, Zhang W. Fractional Refined Composite Multiscale Fuzzy Entropy of International Stock Indices. Entropy. 2019; 21(9):914. https://doi.org/10.3390/e21090914
Chicago/Turabian StyleWu, Zhiyong, and Wei Zhang. 2019. "Fractional Refined Composite Multiscale Fuzzy Entropy of International Stock Indices" Entropy 21, no. 9: 914. https://doi.org/10.3390/e21090914
APA StyleWu, Z., & Zhang, W. (2019). Fractional Refined Composite Multiscale Fuzzy Entropy of International Stock Indices. Entropy, 21(9), 914. https://doi.org/10.3390/e21090914




