Heat Transport in a Spin-Boson Model at Low Temperatures: A Multilayer Multiconfiguration Time-Dependent Hartree Study
Abstract
1. Introduction
2. Methods
2.1. Hamiltonian
2.2. Calculating the Heat Current
2.3. Multilayer Multiconfiguration Time-Dependent Hartree Theory
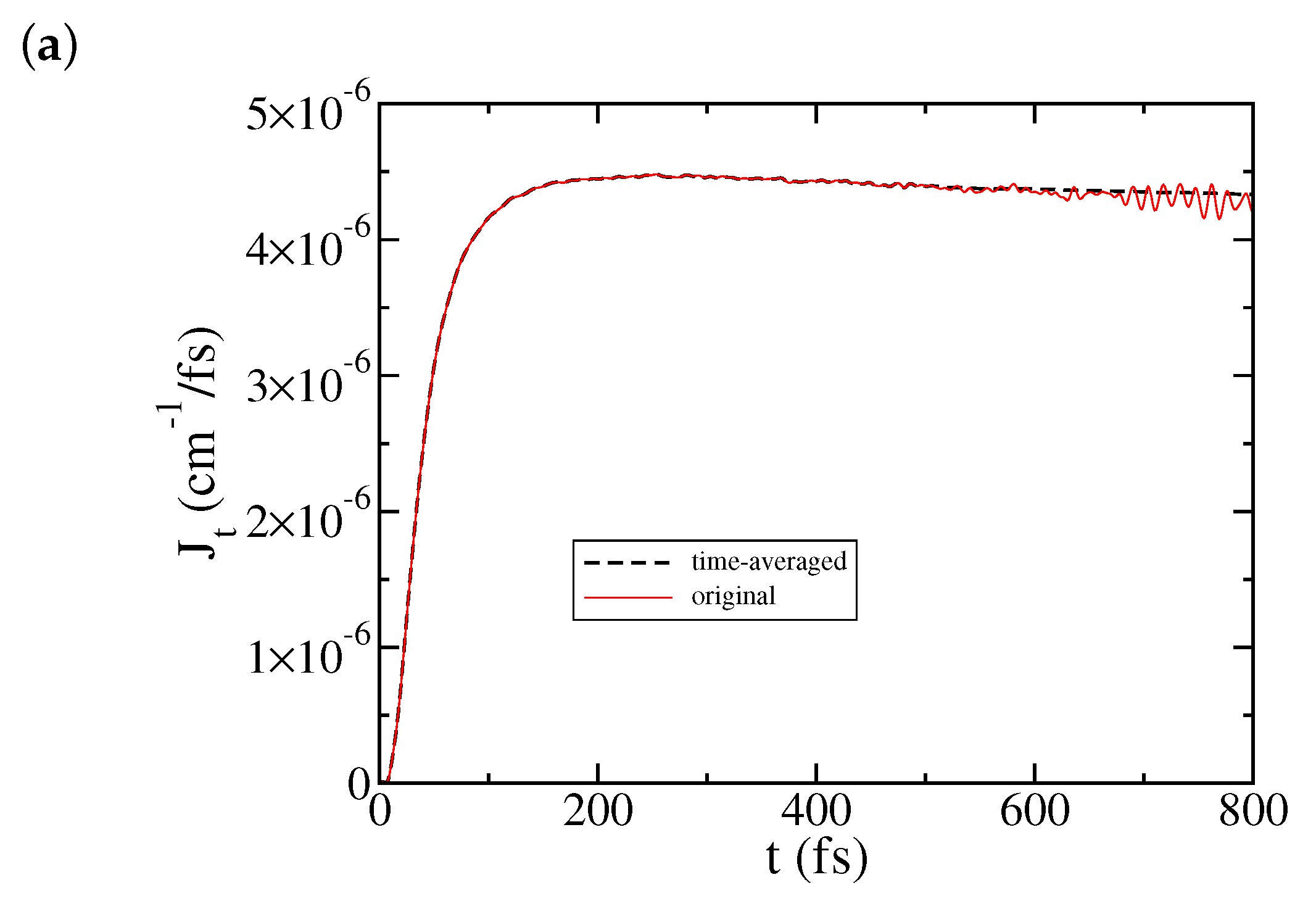
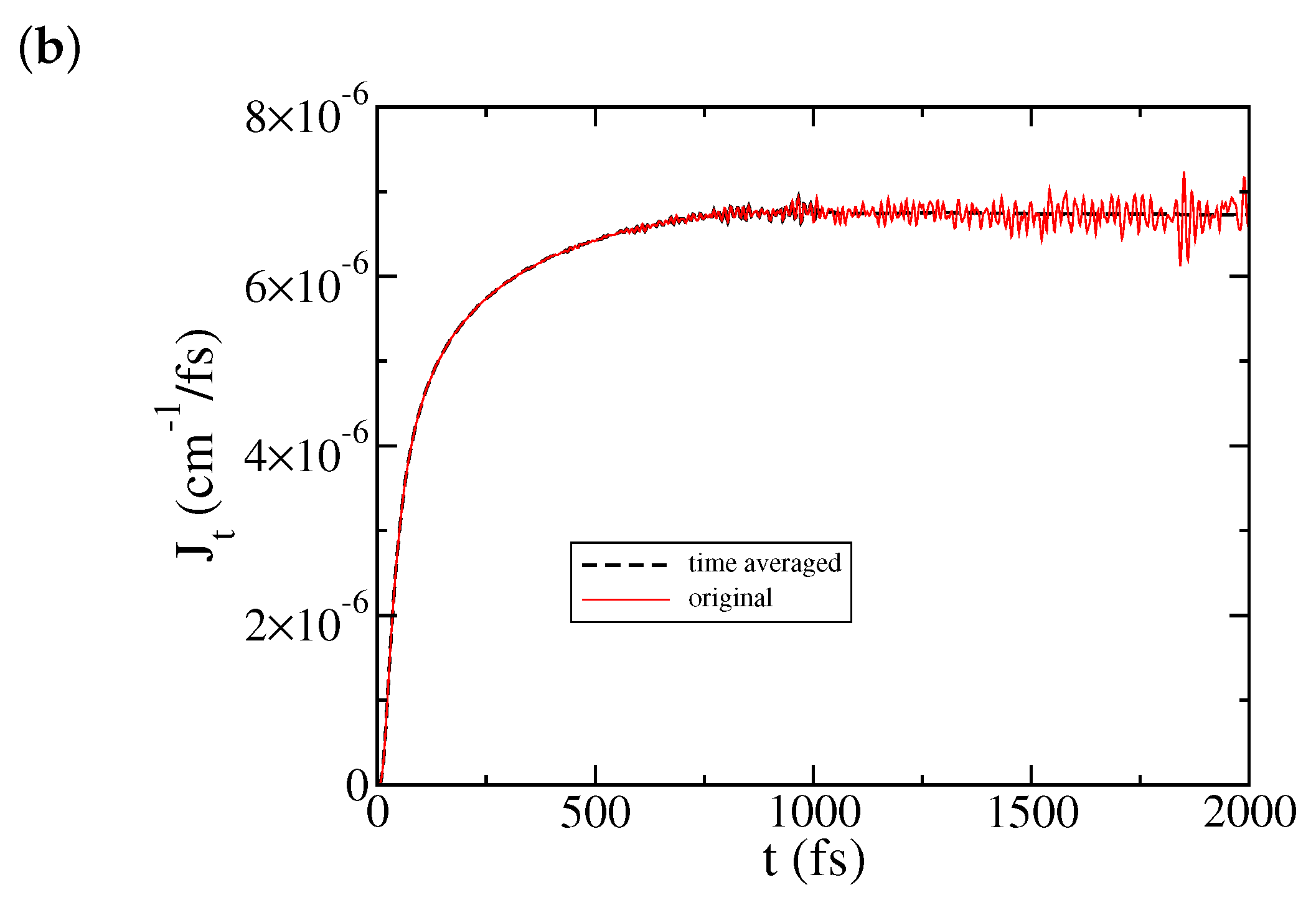
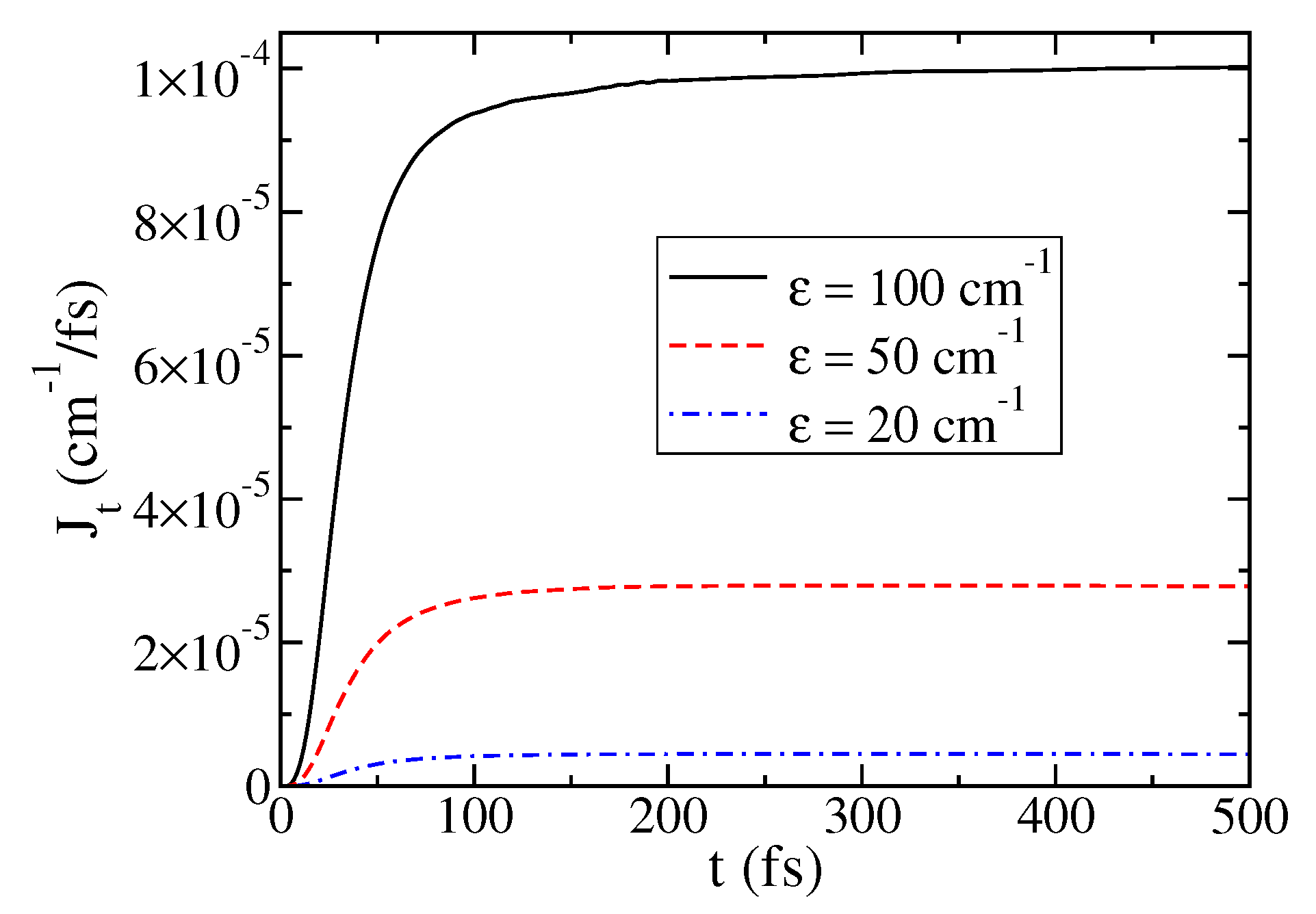
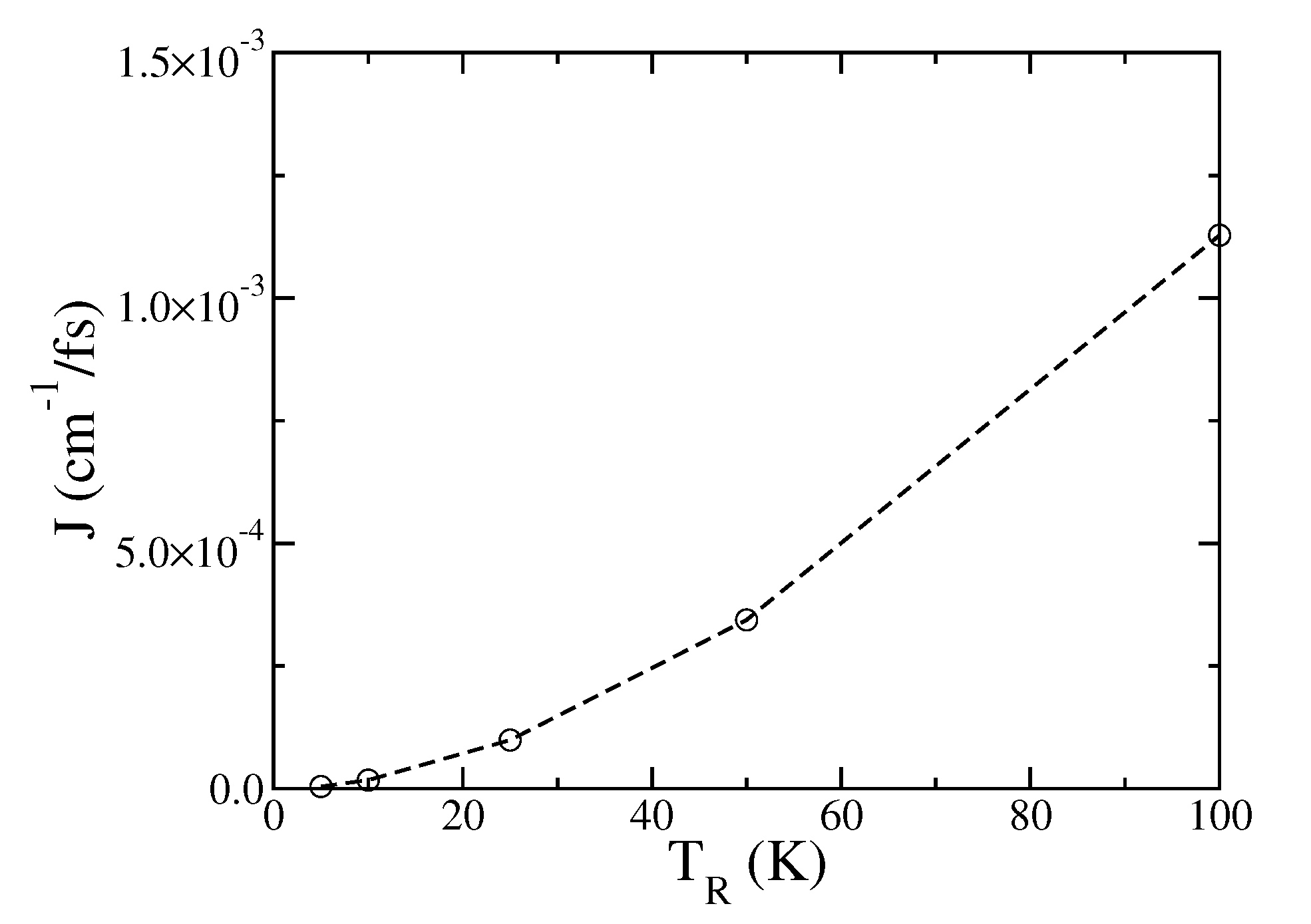
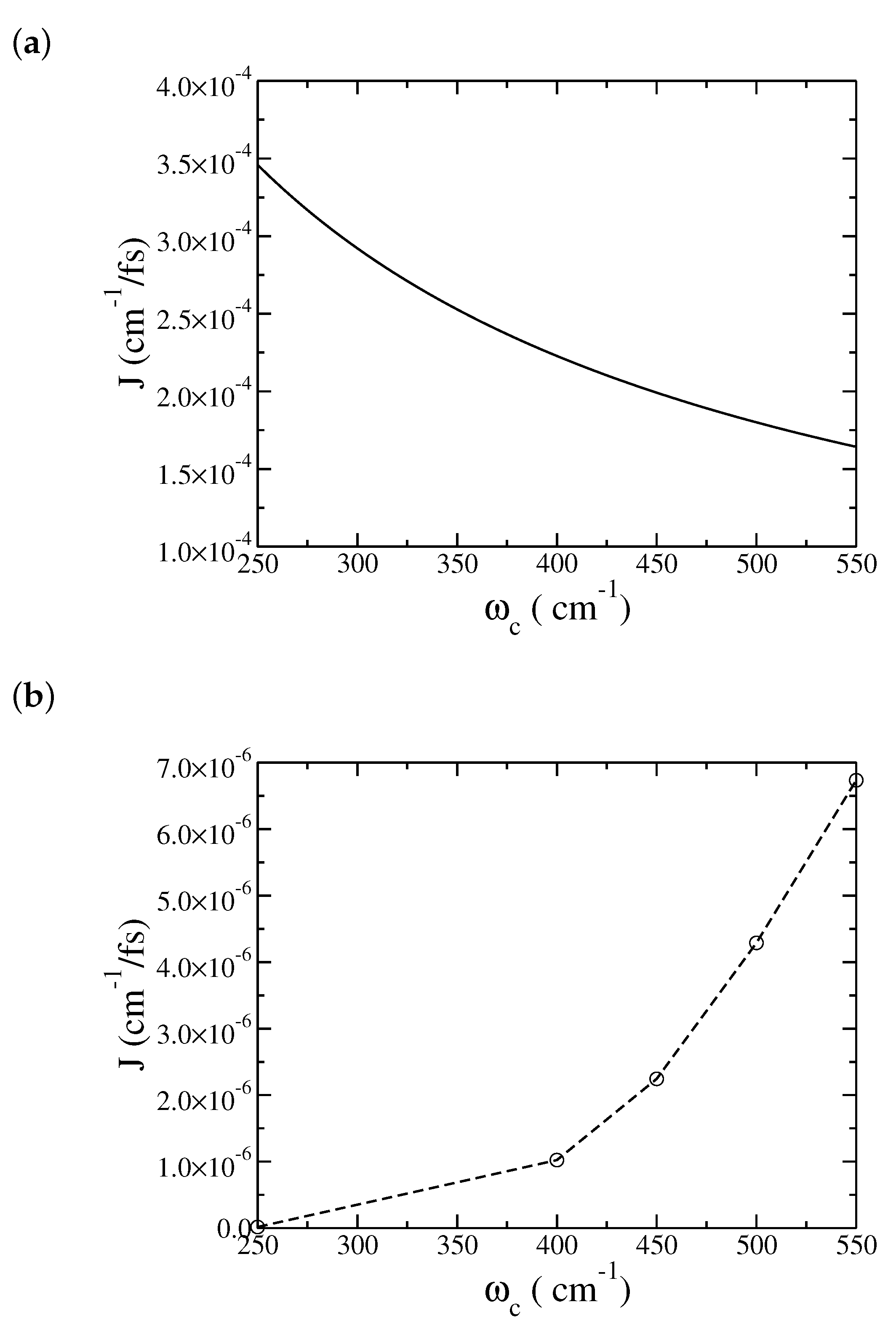
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Montgomery, M.J.; Todorov, T.N.; Sutton, A.P. Power dissipation in nanoscale conductors. J. Phys. Condens. Matter 2002, 14, 5377. [Google Scholar] [CrossRef]
- Chen, Y.C.; Zwolak, M.; Ventra, M.D. Local Heating in Nanoscale Conductors. Nano Lett. 2003, 3, 1691. [Google Scholar] [CrossRef]
- Segal, D.; Nitzan, A.; Hänggi, P. Thermal conductance through molecular wires. J. Chem. Phys. 2003, 119, 6840. [Google Scholar] [CrossRef]
- Huang, Z.F.; Xu, B.Q.; Chen, Y.C.; Ventra, M.D.; Tao, N.J. Measurement of Current-Induced Local Heating in a Single Molecule Junction. Nano Lett. 2006, 6, 1240. [Google Scholar] [CrossRef]
- Pecchia, A.; Romano, G.; Carlo, A.D. Theory of heat dissipation in molecular electronics. Phys. Rev. B 2007, 75, 035401. [Google Scholar] [CrossRef]
- Ioffe, Z.; Shamai, T.; Ophir, A.; Noy, G.; Yutsis, I.; Kfir, K.; Chesnovsky, O.; Selzer, Y. Detection of heating in current-carrying molecular junctions by Raman scattering. Nat. Nanotechnol. 2008, 3, 727. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.; Nitzan, A. Spin-boson thermal rectifier. Phys. Rev. Lett. 2005, 94, 034301. [Google Scholar] [CrossRef]
- Segal, D.; Nitzan, A. Heat rectification in molecular junctions. J. Chem. Phys. 2005, 122, 194704. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.; Nitzan, A. Molecular heat pump. Phys. Rev. E 2006, 73, 026109. [Google Scholar] [CrossRef] [PubMed]
- Redfield, A.G. On the Theory of Relaxation Processes. IBM J. 1957, 1, 19. [Google Scholar] [CrossRef]
- Redfield, A.G. The Theory of Relaxation Processes. Adv. Magn. Reson. 1965, 1, 1. [Google Scholar]
- Segal, D. Current fluctuations in quantum absorption refrigerators. Phys. Rev. E 2018, 97, 052145. [Google Scholar] [CrossRef] [PubMed]
- Friedman, H.M.; Agarwalla, B.K.; Segal, D. Quantum energy exchange and refrigeration: A full-counting statistics approach. New J. Phys. 2018, 20, 083026. [Google Scholar] [CrossRef]
- Jiang, J.H.; Kulkarni, M.; Segal, D.; Imry, Y. Phonon thermoelectric transistors and rectifiers. Phys. Rev. B 2015, 92, 045309. [Google Scholar] [CrossRef]
- Chen, R.; Sharony, I.; Nitzan, A. Local Atomic Heat Currents and Classical Interference in Single-Molecule Heat Conduction. J. Phys. Chem. Lett. 2020, 11, 4261–4268. [Google Scholar] [CrossRef] [PubMed]
- Velizhanin, K.A.; Thoss, M.; Wang, H. Meir-Wingreen formula for heat transport in a spin-boson nanojunction model. J. Chem. Phys. 2010, 133, 084503. [Google Scholar] [CrossRef]
- Wang, C.; Ren, J.; Cao, J. Nonequilibrium Energy Transfer at Nanoscale: A Unified Theory from Weak to Strong Coupling. Sci. Rep. 2015, 5, 11787. [Google Scholar] [CrossRef]
- Xu, D.; Cao, J. Non-canonical distribution and non-equilibrium transport beyond weak system-bath coupling regime: A polaron transformation approach. Front. Phys. 2016, 11, 110308. [Google Scholar] [CrossRef]
- Wang, C.; Ren, J.; Cao, J. Unifying quantum heat transfer in a nonequilibrium spin-boson model with full counting statistics. Phys. Rev. A 2017, 95, 023610. [Google Scholar] [CrossRef]
- Liu, J.; Hsieh, C.Y.; Wu, C.; Cao, J. Frequency-dependent current noise in quantum heat transfer: A unified polaron calculation. J. Chem. Phys. 2018, 148, 234104. [Google Scholar] [CrossRef]
- Duan, C.; Hsieh, C.Y.; Liu, J.; Wu, J.; Cao, J. Unusual Transport Properties with Noncommutative System–Bath Coupling Operators. J. Phys. Chem. Lett. 2020, 11, 4080–4085. [Google Scholar] [PubMed]
- Hsieh, C.; Liu, J.; Duan, C.; Cao, J. A Nonequilibrium Variational Polaron Theory to Study Quantum Heat Transport. J. Phys. Chem. C 2019, 123, 17196–17204. [Google Scholar]
- Agarwalla, B.K.; Segal, D. Energy current and its statistics in the nonequilibrium spin-boson model: Majorana fermion representation. New J. Phys. 2017, 19, 043030. [Google Scholar]
- Liu, J.; Hsieh, C.Y.; Segal, D.; Hanna, G. Heat transfer statistics in mixed quantum-classical systems. J. Chem. Phys. 2018, 149, 224104. [Google Scholar] [PubMed]
- Kilgour, M.; Agarwalla, B.K.; Segal, D. Path-integral methodology and simulations of quantum thermal transport: Full counting statistics approach. J. Chem. Phys. 2019, 150, 084111. [Google Scholar] [PubMed]
- Liu, H.; Wang, C.; Wang, L.Q.; Ren, J. Strong system-bath coupling induces negative differential thermal conductance and heat amplification in nonequilibrium two-qubit systems. Phys. Rev. E 2019, 99, 032114. [Google Scholar] [PubMed]
- Velizhanin, K.A.; Wang, H.; Thoss, M. Heat transport through model molecular junctions: A multilayer multiconfiguration time-dependent Hartree approach. Chem. Phys. Lett. 2008, 460, 325. [Google Scholar]
- Wang, H.; Thoss, M. Multilayer formulation of the multiconfiguration time-dependent Hartree theory. J. Chem. Phys. 2003, 119, 1289. [Google Scholar]
- Wang, H. Multilayer Multiconfiguration Time-Dependent Hartree Theory. J. Phys. Chem. A 2015, 119, 7951. [Google Scholar]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1. [Google Scholar]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599. [Google Scholar]
- Wang, H.; Shao, S. Dynamics of a two-level system coupled to a bath of spins. J. Chem. Phys. 2012, 137, 22A504. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Shao, J.; Wang, H. Dynamics of electron transfer in complex glassy environment modeled by the Cole-Davidson spectral density. Mol. Phys. 2012, 110, 581. [Google Scholar] [CrossRef]
- Wang, H. Iterative Calculation of Energy Eigenstates Employing the Multilayer Multiconfiguration Time-Dependent Hartree Theory. J. Phys. Chem. A 2014, 117, 9253. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Shao, J. Quantum Phase Transition in the Spin-Boson Model: A Multilayer Multiconfiguration Time-Dependent Hartree Study. J. Phys. Chem. A 2019, 123, 1882. [Google Scholar] [PubMed]
- Wang, H. Basis set approach to the quantum dissipative dynamics: Application of the multiconfiguration time-dependent Hartree method to the spin-boson problem. J. Chem. Phys. 2000, 113, 9948. [Google Scholar]
- Wang, H.; Skinner, D.E.; Thoss, M. Calculation of reactive flux correlation functions for systems in a condensed phase environment: A multilayer multi-configuration time-dependent Hartree approach. J. Chem. Phys. 2006, 125, 174502. [Google Scholar]
- Wang, H.; Thoss, M. Quantum mechanical evaluation of the Boltzmann operator in correlation functions for large molecular systems: A multilayer multi-configuration time-dependent Hartree approach. J. Chem. Phys. 2006, 124, 034114. [Google Scholar] [CrossRef]
- Goldberg, A.; Shore, B.W. Modelling laser ionisation. J. Phys. B 1978, 11, 3339. [Google Scholar]
- Kosloff, R.; Kosloff, D. Absorbing boundaries for wave propagation problems. J. Comp. Phys. 1986, 63, 363. [Google Scholar] [CrossRef]
- Neuhauser, D.; Baer, M. The application of wave packets to reactive atom-diatom systems: A new approach. J. Chem. Phys. 1989, 91, 4651. [Google Scholar] [CrossRef]
- Seideman, T.; Miller, W.H. Calculation of the cumulative reaction probability via a discrete variable representation with absorbing boundary conditions. J. Chem. Phys. 1992, 96, 4412. [Google Scholar]
- Frenkel, J. Wave Mechanics; Clarendon Press: Oxford, UK, 1934. [Google Scholar]
- Manthe, U. A multilayer multiconfigurational time-dependent Hartree approach for quantum dynamics on general potential energy surfaces. J. Chem. Phys. 2008, 128, 164116. [Google Scholar] [CrossRef]
- Manthe, U. Layered discrete variable representations and their application within the multiconfigurational time-dependent Hartree approach. J. Chem. Phys. 2009, 130, 054109. [Google Scholar] [CrossRef]
- Vendrell, O.; Meyer, H.D. Multilayer multiconfiguration time-dependent Hartree method: Implementation and applications to a Henon-Heiles Hamiltonian and to pyrazine the description of polyatomic molecules. J. Chem. Phys. 2011, 134, 044135. [Google Scholar] [PubMed]
- Wang, H.; Meyer, H.D. On regularizing the MCTDH equations of motion. J. Chem. Phys. 2018, 148, 124105. [Google Scholar]
- Wang, H.; Meyer, H.D. On regularizing the ML-MCTDH equations of motion. J. Chem. Phys. 2019, 149, 044119. [Google Scholar]
- Wang, H.; Thoss, M. Numerically exact quantum dynamics for indistinguishable particles: The multilayer multiconfiguration time-dependent Hartree theory in second quantization representation. J. Chem. Phys. 2009, 131, 024114. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Lévêque, C.; Madsen, L.B.; Streltsov, A.I.; Alon, O.E. Colloquium: Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. Rev. Mod. Phys. 2020, 92, 011001. [Google Scholar]
- Wang, H.; Liu, X.; Liu, J. Accurate calculation of equilibrium reduced density matrix for the system-bath model: A multilayer multiconfiguration time-dependent Hartree approach and its comparison to a multi-electronic-state path integral molecular dynamics approach. Chin. J. Chem. Phys. 2018, 31, 446. [Google Scholar]
- Grasedyck, L. Hierarchical singular value decomposition of tensors. SIAM J. Matrix Anal. Appl. 2010, 31, 2029. [Google Scholar] [CrossRef]
- Grasedyck, L.; Kressner, D.; Tobler, C. A literature survey of low--rank tensor approximation techniques. GAMM-Mitteilungen 2013, 36, 53. [Google Scholar]
- Lubich, C.; Rohwedder, T.; Schneider, R.; Vandereycken, B. Dynamical Approximation by Hierarchical Tucker and Tensor-Train Tensors. SIAM J. Matrix Anal. Appl. 2013, 34, 470. [Google Scholar] [CrossRef]
- Meyer, H.D.; Manthe, U.; Cederbaum, L.S. The multi-configurational time-dependent Hartree approach. Chem. Phys. Lett. 1990, 165, 73. [Google Scholar]
- Manthe, U.; Meyer, H.D.; Cederbaum, L.S. Wave-Packet Dynamics within the Multiconfiguration Hartree Framework: General Aspects and application to NOCl. J. Chem. Phys. 1992, 97, 3199. [Google Scholar] [CrossRef]
- Beck, M.H.; Jäckle, A.; Worth, G.A.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1. [Google Scholar]
- Meyer, H.D.; Worth, G.A. Quantum molecular dynamics: Propagating wavepackets and density operators using the multiconfiguration time-dependent Hartree (MCTDH) method. Theor. Chem. Acc. 2003, 109, 251. [Google Scholar]
- Tucker, L.R. Some mathematical notes of three-mode factor analysis. Psychometrika 1966, 31, 279. [Google Scholar] [CrossRef]
- Yang, C.H.; Denne, J.; Reed, S.; Wang, H. Computational study on the removal of photolabile protecting groups by photochemical reactions. Comput. Theor. Chem. 2019, 1151, 1. [Google Scholar]
- Pollak, E. Theory of activated rate processes: A new derivation of Kramers expression. J. Chem. Phys. 1986, 85, 865. [Google Scholar]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys. 1990, 62, 251. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-H.; Wang, H. Heat Transport in a Spin-Boson Model at Low Temperatures: A Multilayer Multiconfiguration Time-Dependent Hartree Study. Entropy 2020, 22, 1099. https://doi.org/10.3390/e22101099
Yang C-H, Wang H. Heat Transport in a Spin-Boson Model at Low Temperatures: A Multilayer Multiconfiguration Time-Dependent Hartree Study. Entropy. 2020; 22(10):1099. https://doi.org/10.3390/e22101099
Chicago/Turabian StyleYang, Chou-Hsun, and Haobin Wang. 2020. "Heat Transport in a Spin-Boson Model at Low Temperatures: A Multilayer Multiconfiguration Time-Dependent Hartree Study" Entropy 22, no. 10: 1099. https://doi.org/10.3390/e22101099
APA StyleYang, C.-H., & Wang, H. (2020). Heat Transport in a Spin-Boson Model at Low Temperatures: A Multilayer Multiconfiguration Time-Dependent Hartree Study. Entropy, 22(10), 1099. https://doi.org/10.3390/e22101099





