Abstract
Millimeter wave (mmWave) relying upon the multiple output multiple input (MIMO) is a new potential candidate for fulfilling the huge emerging bandwidth requirements. Due to the short wavelength and the complicated hardware architecture of mmWave MIMO systems, the conventional estimation strategies based on the individual exploitation of sparsity or low rank properties are no longer efficient and hence more modern and advance estimation strategies are required to recapture the targeted channel matrix. Therefore, in this paper, we proposed a novel channel estimation strategy based on the symmetrical version of alternating direction methods of multipliers (S-ADMM), which exploits the sparsity and low rank property of channel altogether in a symmetrical manner. In S-ADMM, at each iteration, the Lagrange multipliers are updated twice which results symmetrical handling of all of the available variables in optimization problem. To validate the proposed algorithm, numerous computer simulations have been carried out which straightforwardly depicts that the S-ADMM performed well in terms of convergence as compared to other benchmark algorithms and also able to provide global optimal solutions for the strictly convex mmWave joint channel estimation optimization problem.
1. Introduction
The standard wireless communication system is exhausted due to the large number of users as well as by the high data speed demands [1]. Millimeter waves (mmWaves) represent a promising candidate with a large amount of unused bandwidth and the ability to support millions of devices at once [2]. mmWaves have very short wavelengths therefore the hardware structure of mmWave relying upon a multiple input multiple output (MIMO) system is unlike the conventional sub 6 Ghz wireless communication system [3]. The smaller wavelength of mmWaves make them perfectly compatible for multi-user MIMO systems accompanied by large antenna arrays. Since the mmWave frequencies are highly directional as compared to lower frequencies therefore they can precisely handle large antenna arrays during the transmission and reception process and a beamforming strategy is required for mmWave MIMO systems. Here the term “beamforming” conventionally refers to the set of smart antenna arrays. Beamforming restricts transmitted signals to a particular desired receiving antenna element available in an antenna array at the receiver’s end. Consequently, for achieving the high array, diversity and multiplexing gain, beamforming plays an important role in mmWave MIMO systems [4]. Generally, three kind of beamforming techniques—analog beamforming (ABF), digital beamforming (DBF) and hybrid beamforming (HBF)—are used. ABF steers the ultra linear array (ULA) output using a single RF chain and phase shifters [5]. However, the analog structure cannot be equipped with multiplexing advantages. On the contrary, DBF offers the flexibility needed to support multi-stream data transmission, but the hardware is expensive and power consuming as it consists of separate RF chains (with ADC/DAC) for every antenna element in the uniform linear array (ULA) [5]. Therefore, due to the aforementioned limitations, ABF and DBF are not considered suitable for mmWave MIMO systems and hence the HBF technique which combines both analog and digital beamforming architectures and provides a better trade-off between cost/complexity and spectral efficiency is used for enabling the communication in mmWave MIMO systems [6,7].
In any wireless communication system, efficient estimation of the wireless channels at the receiver’s end is the only way to ensure the quality of transmitted symbols. Apparently, channel estimation is a vulnerable task for any type of wireless communication system. For achieving the potential advantages of mmWave MIMO system, obtaining the accurate knowledge of channel state information (CSI) is critically important. As the mmWave MIMO system’s operating regime and hardware constraints are different than those of conventional wireless communication systems therefore new channel estimation strategies are needed. There are several popular channel estimation techniques for mmWave MIMO systems are already available in the research domain. These strategies are based on compressive sensing (CS) where the sparsity of the channel is exploited in the angular or beamspace domain [8,9,10,11,12,13,14] or due to the narrow angle spread of individual clusters, the low rank properties of channel covariance matrices (CCMs) are being investigated [15]. The most common approach for the estimation of CSI is to consider it as a CS problem [16]. In [17,18] the estimation techniques require receiver feedback which can further increase the pilot demands and reduce the spectral efficiency of the system. Statics dictionaries and beam training methods are also discussed in [13,19,20,21,22]. These methods do not require receiver feedback and they exploit the static dictionaries of the channel matrix which usually have the information of angle of arrival (AoA) and angle of departure (AoD), but for a larger number of training overheads, the static dictionaries generate errors related to discretization and power leakage. One of the most popular CS approaches is orthogonal matching pursuit (OMP), described in [23]. Exploitation of angle information for sparse channel estimation is described in [18] in which a fast discrete Fourier transform (DFT)-based spatial rotation algorithm is designed to contemplate most of the channel power on limited DFT grids and efficiently obtain the angle information for both frequency division duplex (FDD) as well as time division duplex (TDD) systems [24]. Specifically, the array signal processing-based channel estimation scheme, where the angle information of the user is exploited to simplify channel estimation is illustrated in [24]. A CCM-based approach are described in [25]. In any typical scattering atmosphere, [25] demonstrates the low-rank feature of the CCM’s in mmWave communications and to curtail the effective dimensions of the channel, it elaborates the collective spatial division multiplexing algorithm. The channel estimation problem is assigned as a quadratic semidefinite programming (SDP) problem where the low-rank structure of the CCMs are used and solved by using a polynomial SDP method is interpreted in [26]. In [27], a virtual channel with common sparsity because users are sharing the same local scatters, is explained in which the information of unitary dictionary matrix is available at a base station (BS). A comprehensive study on signal processing techniques used for mmWave MIMO communications is briefly explained in [28].
Alternating direction method of multipliers (ADMM) was recently proposed in [29] and it has attracted extensive attention due to its simple implementation. It is widely used in distributed machine learning [30], image processing [31], statistical signal processing [32] and many more fields. ADMM breaks any complicated optimization problem into several small subproblems therefore one can derive the optimal solutions very easily [29]. ADMM is used for the narrowband and wideband channel estimation of mmWave MIMO system by exploiting the sparsity and low rank properties of channel were jointly exploited for efficient CSI estimation in [16,33]. An extended version of ADMM (Ex-ADMM) with a Fortin and Glowinski’s constant (i.e., the relaxation parameter) is also used for the narrowband channel estimation of mmWave MIMO systems in [34]. A symmetric version of ADMM (S-ADMM) came into the research domain very recently [35,36]. Within this scheme, the Lagrange multipliers are updated twice in a symmetrical manner [35]. The studies indicates that the convergence of S-ADMM with larger step sizes, can be enlarged with the help of Fortin and Glowinski’s constant [35]. The symmetrical formation of ADMM also results an enhancement in the overall performance of the system.
The contributions of this paper can be summarized as follows:
- (1)
- A novel S-ADMM based channel estimation scheme for the estimation of mmWave channels relying on a MIMO system is proposed. After updating the Lagrangian multipliers twice, a symmetrical version of ADMM can optimized the intermediate and essential variables in a symmetrical order. In addition with the Fortin and Glowinski’s constant which is generally known as a relaxation parameter, the convergence of the algorithm can be enhanced. In this paper, the overrelaxed version of relaxation parameter have been considered for simulation and experiments.
- (2)
- To explain the superiority of the proposed scheme, various different popular start-of-art schemes namely, OMP [13] Vector Message Approximation Passing (VAMP) [37], Ex-ADMM [34], ADMM [33], Block Orthogonal Matching Pursuit (BOMP) [38], Generalized Approximate Message Passing with Gaussian Mixture (GAMP-GM) [39,40] and Singular Value Thresholding (SVT) [41] have been considered for the comparison. Furthermore, the eminence of the proposed scheme is explained in terms of normalized mean squared error (NMSE), achievable spectral efficiency (ASE), convergence, effect on the number of scatterers and the number of possible paths.
The rest of the paper is assembled as follows: Section 2 described the System Model used for various studies within this paper. The problem formulation for the channel estimation of mmWave MIMO system along with a detailed description of proposed scheme followed by the algorithm terminologies and complexity analysis is depicted in Section 3. Simulation and results are explained in Section 4 and finally, last but not least, conclusion remarks are elucidated in Section 5.
Notation: The notation used within this paper is described in Table 1.

Table 1.
Notation.
2. System Model
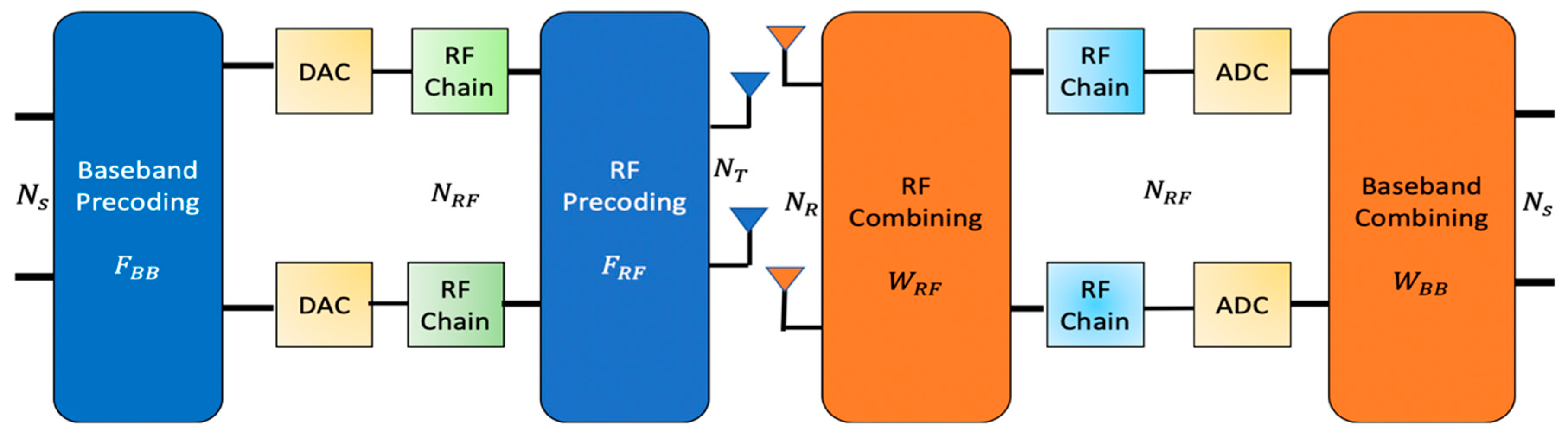
A hybrid mmWave MIMO system is a constellation of two continuous segments namely, a digital MIMO baseband and an analog RF precoder at the transmitter section while at the receiver section it has two successive joint segments of a RF combiner and a baseband combiner section For our studies, the HBF structure explained in [19] is adopted. Wherein, a point to point mmWave MIMO system, equipped with transmit and receive antennas at base station (BS) and mobile station (MS), respectively, is considered [42] as depicted in Figure 1.
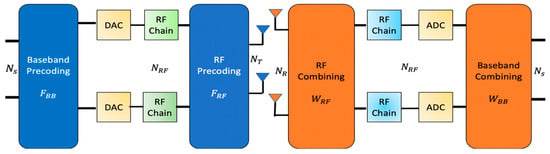
Figure 1.
Hybrid mmWave MIMO architecture.
At the transmitter and receiver section, this system is provided with parallel data streams and radio frequency (RF) chains, such that [43,44]. The transmitter section is furnished with RF chains in such a way that . For initiating the communication, the transmitter employed pilot beam patterns, denoted as whereas, at the receiver end, the receiver employed pilot beam patterns, denoted as [13], where a and b are the transmitter’s training precoding vector and receiver’s training combining vector, respectively [13].
After the initial transmission, the received signal matrix Y at the receiver’s end can be determined as:
where, the received signal matrix is the combination of different received vectors, i.e., , alike Y the combining matrix W and precoding matrix F is also representing by the set of different combining and precoding vectors i.e., and , respectively. Here, is the set of transmitted vectors, A is the channel matrix and are independent and identically distributed (I.I.D) complex additive white gaussian noise (AWGN), with zero mean and [34]. For the simplicity of the system, let’s consider that the all pilot symbols are identically similar, therefore, one can assume that . Here expressed the average transmitted pilot power [13,18].
As it is clear from the HBF architecture described in [19], Equation (1) can be re-written on the basis of decomposition of W and F, i.e., and . Therefore:
where, and are the transmitted and received beamforming matrices, respectively. and are the transmitted and received baseband processing matrices, respectively [19]. W is the combiner, such that , and F is the precoder, such that [19].
According to the geometric virtual (GV) model of mmWave MIMO system explained in [12,18], Equation (2) can be further elaborated as:
where, denotes the total number of propagation paths, expressing the complex channel gain of the l-th path, and it can be obtained from the random complex Gaussian distributions, and . and are the array response vectors (ARV) at the transmitters and receivers, respectively [34] (see the references therein). and are the elevation and azimuth AoA and AoD angles at the transmitters and receivers, respectively [34] (see the references therein). The elevation and azimuth AoA and AoD angles can be produced by uniform Laplacian distributions, allocated within the range of 0 and 2
According to [6,45], ARV of a ULA can be expressed as:
where, the wavelength is denoted by , k is the spacing between the antennas and the ARV’s even function is .
Based on the virtual beamspace representation model, Equation (4) can be rewritten in matrix decomposition form [46,47]. Therefore, the channel matrix A can be expressed as:
where the receiver’s and transmitter’s ARV’s in terms of unitary matrices are and [46], respectively and these are expressed as
From the matrix property, and are N × N identity matrix . In Equation (5), Z has the several virtual channel gains of higher amplitude, therefore it is known as sparse matrix and Z .
3. Proposed Channel Estimation Scheme for mmWave MIMO System
In this section, the optimization problem followed by the solution obtained through proposed S-ADMM based scheme is described in detail. Additionally, the computational complexity as well as the algorithm terminology is also discussed briefly.
3.1. Problem Formulation for mmWave MIMO System
Partially observed data are very helpful for completing the missing entries of a low rank matrix [48,49] therefore, to formulate the optimization problem for the channel estimation of mmWave MIMO system, Equation (5) is split into a decomposed version such as , where C defines the submatrix of Z and it has the information of subsampled values of Z.
Thus, to recover the CSI matrix A, the joint optimization problem can be therefore illustrated as:
In the cost function described in Equation (6), are treated as the side information of matrix C. These informations are able complete the missing entries of low rank matrix A. The nuclear norm on matrix A ensured its low rankness and the on C ensured the sparsity on C. and are known as the weighting factors and it generally rely upon the number of propagation path. These weighting factors are always assumed to be a positive number i.e., , [48].
3.2. Proposed S-ADMM Scheme for mmWave MIMO System
The optimization problem described in Equation (6) is clearly a two objective strict convex function. Thus, solution of Equation (6) can be obtained by numerous methods. Generally, alternating optimization techniques (AOTs) are the best selection for solving Equation (6). ADMM [29] is the one of the best known AOT’s for solving the strict convex problems. Therefore, to get the optimal solutions of Equation (6), reformulate it and introduced two auxiliary matrices, and . Hence, the new targeted optimization problem can be expressed as:
The new cost function defined in Equation (7) contains different information related to different parameters. The first term holds the side information of low rank matrix A. The second term contains the information of subsampled virtual channel gain. Third and fourth term have the statistics of discretization errors and AWGN noise, respectively. Subsequently, Equation (7) can be written under the augmented Lagrangian function (ALF) as follows:
In Equation (8), are assigned as Lagrange multipliers also known as dual variables. On the other side is contemplated as the step size of the algorithm and it always been consider as a positive integer. For the better understanding of S-ADMM, the ADMM is described first and then the symmetrical version is discussed on the base of ADMM. ADMM is already used to solve the cost function described in Equation (8) [33] and it generates its order as follows:
The optimal solution of above equations can be obtained very easily as the main targeted cost function gets scattered in to 6 sub parts. Therefore, by following ways the variable described in Equations (9)–(14) can be solved,
3.2.1. Solution of A
The closed-form solution is determined by considering all the terms related to A in Equation (8) and implementing SVT [41] on them. Therefore:
Here, are the side singular vector of the matrices and . is known as SVT operator and the r singular values are denoted by .
3.2.2. Solution of B
For the close form solution of , we consider all the terms related to B in Equation (8) and set it to the zero. Thus:
Here, I illustrate the identity matrix, whereas G , exhibits the k-th row, and is derived by inserting unit values in the zero matrix at its (k,k)-th position as well as H [33,34].
Hence, for (l + 1) iteration of b is:
For unvectorized Equation (19), thus:
3.2.3. Solution of C
For the close form solutions of , separate all the term of C in Equation (8). Therefore:
Here, Equation (21) is considered as the standard least absolute shrinkage and selection operator (LASSO) problem [50]. Therefore, to solve Equation (21), vectorization is performed:
Let us consider, and . Hence, Equation (22) can be equivalently expressed as:
Afterwards, a soft thresholding operator is applied on Equation (23) for (l + 1) iterations:
Here, is known as the scaled version of and . Therefore, is obtained by unvectorizing the :
3.2.4. Solution of D
To get the solution of , we consider all the terms related to D in Equation (8) and set them to zero:
Therefore, the solution of can be expressed as:
The solutions of A, B, C and D can update the Equations (9)–(14). Subsequently, according to Langrage multiplies methods, the dual variables and can be update with help of the A, B, C and D’s solutions.
Algorithm 1 describes the channel estimation method of a mmWave MIMO system via ADMM. Here, the intermediate and essential variable are updated first and the dual variables are updated at the last. As described in [51], Fortin and Glowinski proposed that, attaching a relaxation parameter in ADMM lead to the faster convergence. Therefore, according to the Fortin and Glowinski proposed idea Equations (9)–(14) can be written as:
| Algorithm 1. mmWave MIMO Channel Estimation Scheme via ADMM [33] | |
| Require: | Subsampled matrix , side information matrices and , and the set of indices of observed entries in . |
| Input: | , ,, ,, , and |
| Output: | Estimated output channel matrix Initialization: |
| Step 1: | for l = 0, 1, 2……. |
| Step 2: | Update by using Equation (16). |
| Step 3: | Update by using the Equation (20). |
| Step 4: | Update by using the Equation (25). |
| Step 5: | Update by using the Equation (26). |
| Step 6: | Update by using Equations (13) and (14), respectively. |
| Step7: | end for |
Here, is known as Fortin and Glowinski’s relaxation parameter. Typically, rely in between 0 and , which can be approximated around 0 and 2. Multiplication of relaxation parameter with the is enlarge the step size of ADMM and lead to the faster convergence [51,52,53].
ADMM defined in Equations (27)–(32) is different than the ADMM defined in Equations (9)–(14). To all intents and purposes, there are two distinct families of ADMM, one is derived from the operator splitting framework and the other derived from the Lagrangian splitting [54]. Therefore, except for the notation similarity of the ADMM defined in Equations (9)–(14) and Equations (27)–(32), the ADMM scheme with Fortin and Glowinski’s relaxation parameter is different than the ADMM define in Equations (9)–(14) in nature [35].
As observed in [55,56], the ADMM scheme described in Equations (9)–(14) is an application of the Douglas–Rachford splitting method (DRSM) in [57,58] to the dual of Equations (9)–(14). However, If the Peaceman–Rachford splitting method (PRSM), which is described in [58,59] is implemented on ADMM described in Equations (27)–(32), the resultant new ADMM can be expressed as:
The above described scheme in Equations (33)–(40) is known as symmetrical ADMM (S-ADMM) wherein, all the variables are treated in a symmetrical manner.
3.3. Algorithm Elucidation
The proposed S-ADMM scheme for the channel estimation of a mmWave MIMO system is described in Algorithm 2. Within this scheme, the matrix has the non-zero uniformly distributed entries at their respective ij-th position in such a way that [60,61]. Notably, these non-zero values are chosen in a haphazard manner. Therefore, it can be argued that the matrix has M ones and zeros. Matrix is followed by a subsampled matrix . Thus, the entries of is also followed by the entries of ., so the positions of non-zero entries in are also similar to the positions on non-zero entries in . The error caused during the estimation of A depends upon the estimation accuracy of ’s elements and the M non-zero values of [34]. The threshold point, where the training symbols length are equal to the position of the non-zero entries in A i.e., T = M and M , is considered as a stopping criterion for the proposed S-ADMM scheme.
| Algorithm 2. Proposed S-ADMM based mmWave MIMO Channel Estimation Scheme | |
| Require: | Subsampled matrix , side information matrices and , and the set of indices of observed entries in . |
| Input: | , ,, ,, , and |
| Output: | Estimated output channel matrix Initialization: |
| Step 1: | for l = 0, 1, 2……. |
| Step 2: | Update by using Equation (33) and it gets updated from the solution in Equation (16) |
| Step 3: | Update and by using Equations (34) and (35), respectively. |
| Step 4: | Update by using the Equation (36) and it used solution described in Equation (20) |
| Step 5: | Update by using the Equation (37) and the solution of C is updated by Equation (25). |
| Step 6: | Update by using the Equation (38) and the solution of D is provided by Equation (26). |
| Step 7: | Update by using Equations (39) to (40), respectively. |
| Step8: | end for |
3.4. Complexity Analysis
In the proposed S-ADMM scheme, step 2 is the most important and decisive part. In step 2, SVT operator is implemented on the non-squared matrix A. The SVT is nothing but another version of singular value decomposition (SVD), where the targeted matrix is transformed in to an orthogonal matrix to ensure orthogonality. Therefore, the order of complexity required to compute the step 2 is proportional to [62]. Step 4 of the proposed scheme has the solutions of the Equation (18) is illustrated by the inversion of . However, this matrix is a diagonal matrix, therefore, the required complexity is . In step 6, the pseudo-inverse of has to be calculated which needs the calculation and conversion of the Gram matrix [16]. However, this step is the very expensive and cost huge computational load. Nonetheless, is already noted as a presiding diagonal matrix, hence gradient-based iterative algorithms is used to lower the complexity order to [63]. The rest of the steps are acting as a matrix- matrix and matrix- vector products, which inherently needs lower computational power.
4. Simulation and Results
In this section, simulations are carried out and results are explained in detail. To illustrate the preeminence of the proposed S-ADMM scheme, by considering the parameters with their respective values listed in Table 2, a simulation is performed and the detailed results are explained.

Table 2.
Simulation Parameters.
Seven different state-of-art benchmark algorithms namely: OMP, VAMP, ADMM, Ex-ADMM, GAMP-GM, BOMP and SVT are taken into account for the comparison with proposed S-ADMM algorithm. The basic and working methodology of all five benchmark algorithms are entirely different from each other which is the main motivation to consider them for performance comparison with our proposed scheme. The performance of the proposed S-ADMM scheme is compared with these benchmarks in term of NMSE, ASE, convergence and effects of scatterers as well as with the number of paths.
4.1. NMSE Comparison
To demonstrate the performance of S-ADMM in terms of NMSE, low training symbol lengths i.e., T = 400 and high training symbol lengths T = 1200, is considered for simulation. The relation is used to calculate the NMSE is described as follows:
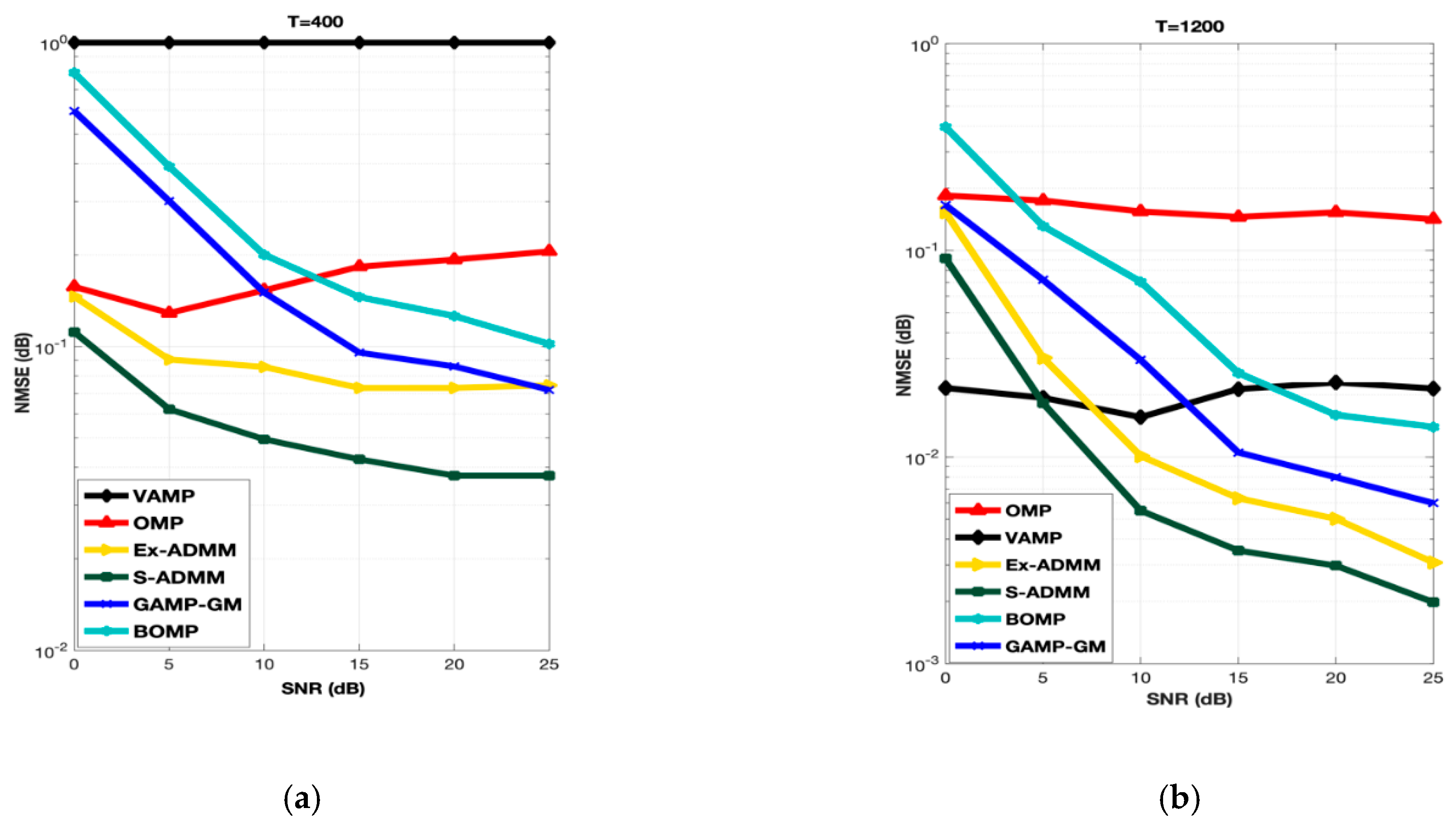
Performance of OMP is moderated at low SNR points (i.e., <5 dB) but as the SNR is increasing from low to mid and then to the high the performance is started decreasing. This happens due to the discretization error caused in dictionary matrix. GAMP-GM approximate any vector in to a scaler which reduce the complexity of the algorithm and an enhancement in performance is beheld. Hence, it is clear from Figure 2 that the performance of GAMP-GM is unquestionably better than that of another approximate message passing algorithm VAMP for small and high training symbol lengths. For T = 400 and 1200, at low- to mid-SNR points, the performance of GAMP-GM is very significant but as the SNR range is increased from mid to high, the performance is slightly getting worse. The reason behind this is that the GAMP-GM diverges with the overcomplete dictionary matrices resulting from beam domain quantization. BOMP is another popular basic pursuit algorithm for the recovery of sparse signals which exhibits the additional structure in the form of the nonzero coefficients occurring in channel matrix. Such signals are referred to as block-sparse. In Figure 2, for T = 400 at low to mid SNR points, the performance of BOMP is trail behind the OMP but as the SNR range is increased from mid to high the performance of BOMP is getting much better as compare to OMP. For T = 1200, BOMP outperformed OMP because OMP is not capable enough to recover the large training symbols. This happens as the BOMP exploits the block sparse structure of channel matrix. Therefore, large and small training symbols can be recovered by using BOMP. Practically, in BOMP, the spatial frequencies corresponding to the AoA and AoD of each path may not fall exactly in the grid points of DFT matrices of ULA size which caused the performance degradation. The Ex-ADMM is an extension of ADMM and it performs well at almost all SNR points. Although, the performance of the S-ADMM is better than all other benchmark algorithms. The reason behind that is, the Ex-ADMM only use relaxation factor to enlarge the step size but the S-ADMM make the step size enlarger in addition with the symmetrical treatment for all variables. When high training symbols length i.e., T = 1200 are chosen for simulation, VAMP improved its performance at almost all SNR points. On the contrary, the performance of OMP remain in the same condition due to the fact that, at high SNR and large training symbols length, OMP suffered from discretization error and it is not capable to recover the transmitted symbols properly. Ex-ADMM keep performing at T = 1200 mid to high SNR points but it is underperformed by S-ADMM.
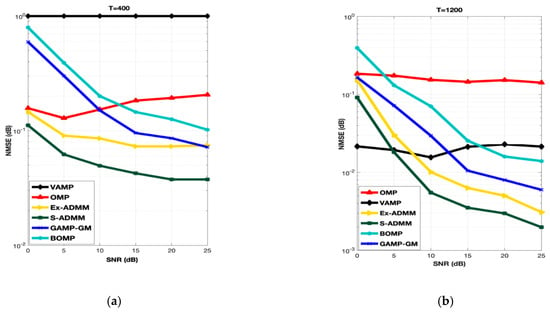
Figure 2.
NMSE performance of S-ADMM for T = 400 (a) and T = 1200 (b) at 30 dB SNR.
4.2. ASE Comparison
For the performance evaluation in terms of ASE of proposed S-ADMM scheme, similar as NMSE, low (T = 400) and high (T = 1200) training symbols lengths have been considered for simulation. The relation assigned to calculate the ASE [65,66] is:
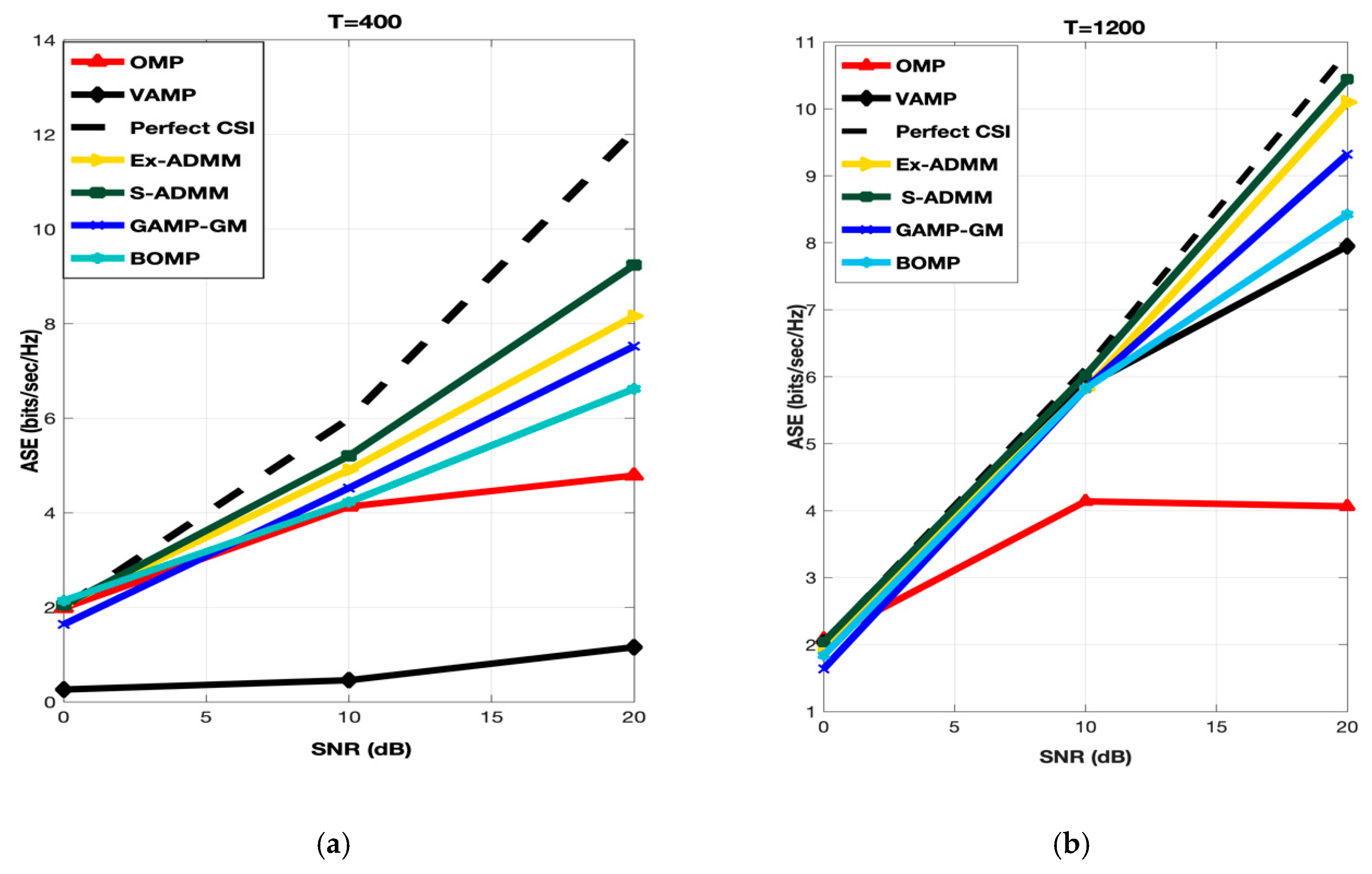
Figure 3 explains the performance evaluation of the proposed S-ADMM scheme in comparison with OMP, VAMP, BOMP, GAMP-GM and Ex-ADMM. In the case of OMP, for T = 400 in all the SNR range, it performed ordinarily but the performance of OMP is getting worse as the length of training lengths as well as the SNR range are increasing. For T = 400 at low to mid SNR range the performance of GAMP-GM is nearly similar to Ex-ADMM and BOMP but as the SNR range is increased from mid to high, GAMP-GM outperformed BOMP, OMP and VAMP. For T = 1200 at low to mid SNR range, GAMP-GM are very close to VAMP, Ex-ADMM, BOMP and proposed S-ADMM. As the SNR points are increasing from mid to high, the performance of GAMP-GM is improving linearly and it outperformed the VAMP, BOMP and OMP. In case of BOMP, for T = 400 and 1200 at low to mid SNR range, it performed better than the OMP and VAMP. Same pattern is observed at mid to high SNR range. Therefore, one can see that, the performance of BOMP is better than the OMP and VAMP for all SNR points as well as for all training symbol lengths. As discussed earlier, VAMP is not designed for low training symbols therefore it performed worst for T = 400 at almost every SNR range. For high training symbols length (i.e., T = 1200), VAMP shows a significant improvement and performed very well from low to mid as well as from mid to high SNR points. As a matter of fact, VAMP outperformed OMP at all SNR points. Interestingly, the performance of the proposed S-ADMM and Ex-ADMM are almost equal at all SNR points. However, the performance of proposed S-ADMM is slightly improved as compared to Ex-ADMM. In conclusion, the proposed S-ADMM outperformed all other benchmark algorithms at all SNR points for low training symbols length.
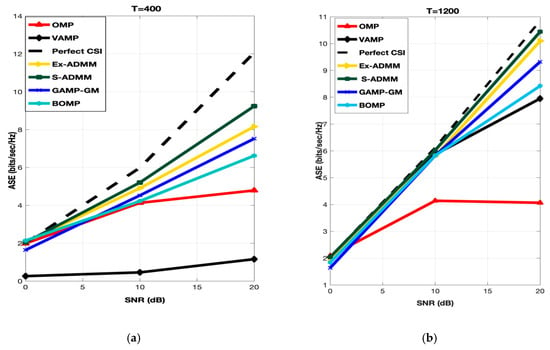
Figure 3.
ASE performance of S-ADMM at T = 400 (a) and T = 1200 (b).
4.3. Comparison of Convergence
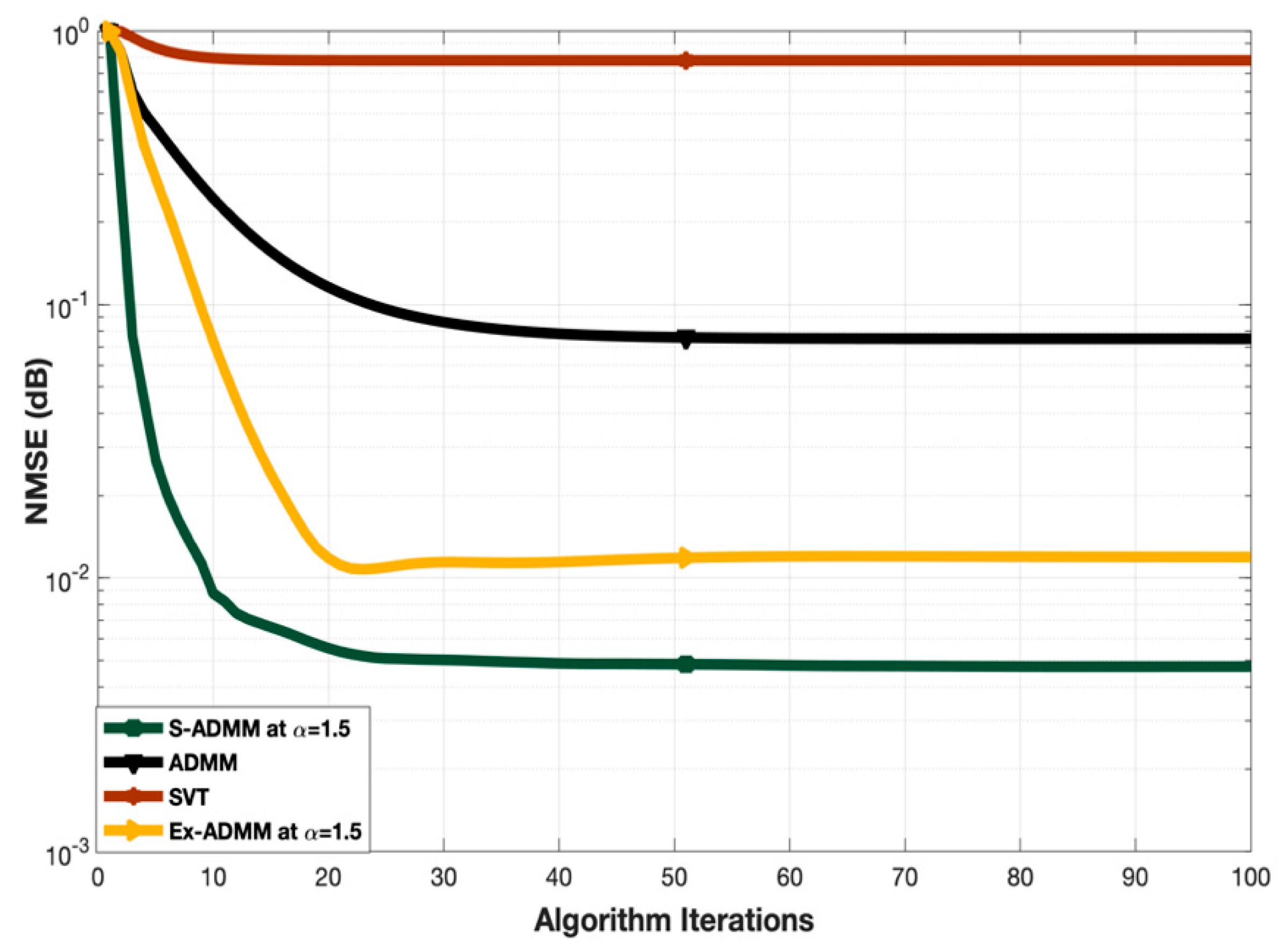
Figure 4 illustrates the convergence of the proposed S-ADMM scheme. In order to compare the convergence, benchmarks SVT, ADMM and Ex-ADMM have been considered. The number of training symbols is fixed at 400 as well as the relaxation parameter for Ex-ADMM and proposed S-ADMM is set to be 1.5. As one can see from Figure 4, the SVT converges fast as it is a one stage direct method but its NMSE performance is worse than all of the other benchmarks and the proposed S-ADMM. The convergence of ADMM and Ex-ADMM is almost identical and moderate but the NMSE performance of Ex-ADMM is better than that of ADMM. Convergence of the proposed S-ADMM is better than that of all other benchmarks and its NMSE performance also outperforms the others. Eventually, the SVT started converging around 5–10 iterations. The ADMM and Ex-ADMM take around 15–20 iterations to converge. However, the proposed S-ADMM started converging around 7–12 iterations. Therefore, one can observe that the proposed S-ADMM outperformed all other state-of-art benchmark algorithms in terms of convergence which makes it faster than all the other described methods.
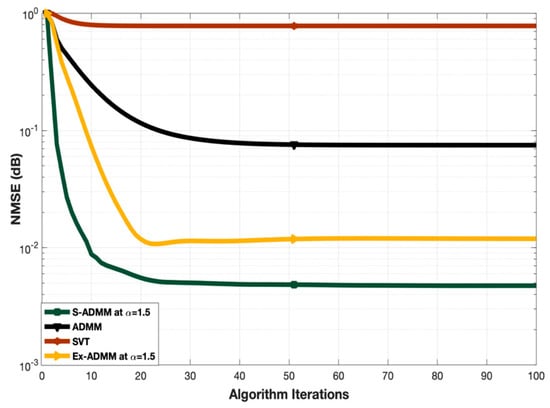
Figure 4.
Convergence comparison at .
4.4. Effect on Number of Scatterers and Paths
Figure 5 elaborates the performance of the proposed S-ADMM scheme over several scatterers and the number of paths. It is observed that as the number of scatterers and number channel paths is inversely proportional to the NMSE performance of the system.
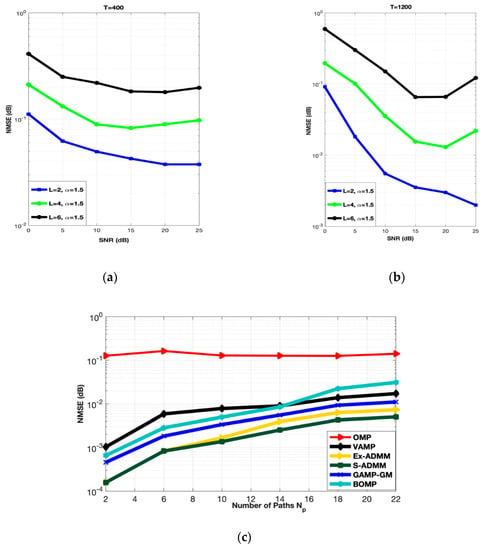
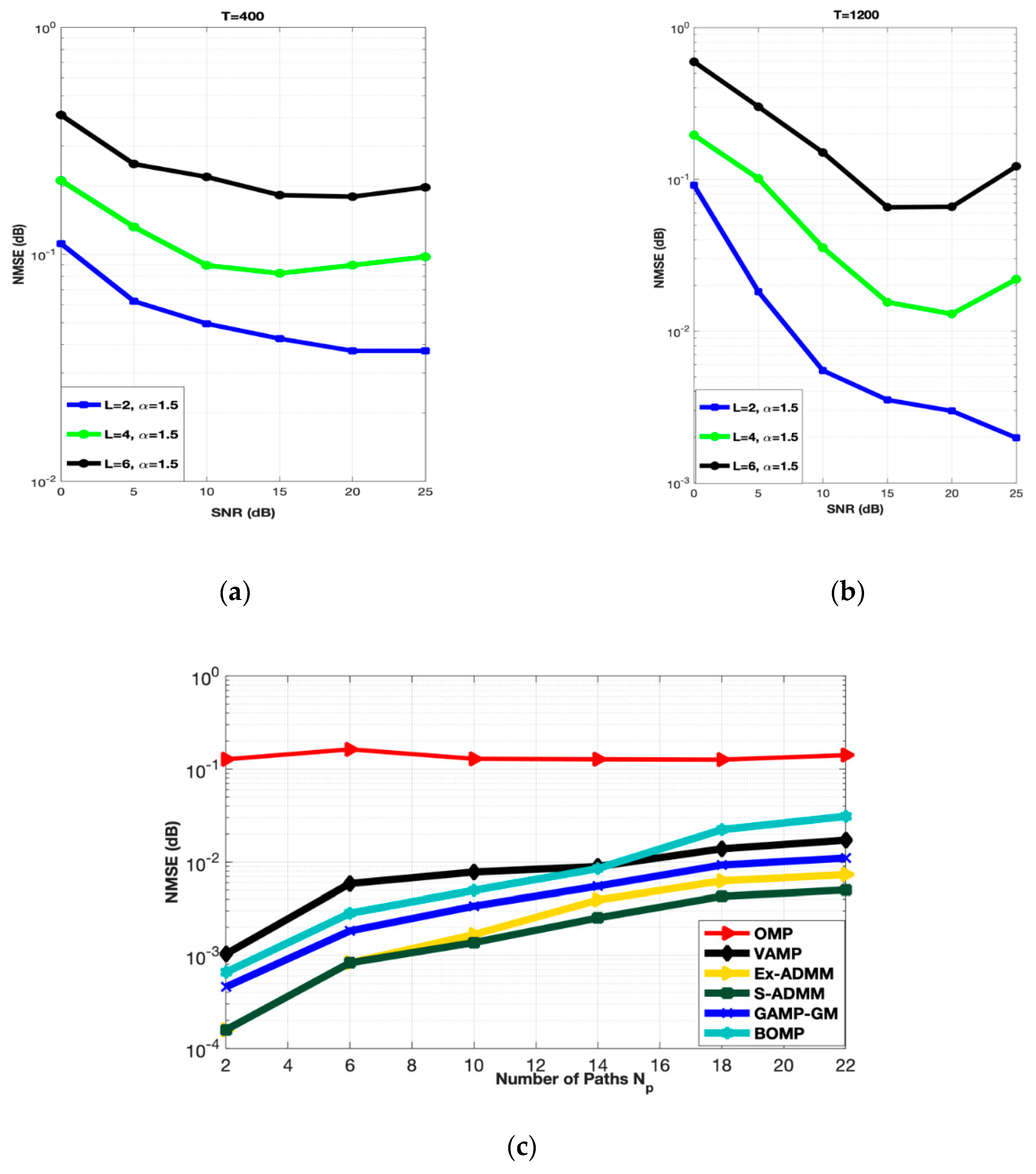
Figure 5.
(a,b) Number of scatterers vs. NMSE at 30 dB SNR. (c) Number of paths vs. NMSE.
Figure 5a demonstrates the performance of the proposed S-ADMM scheme for low training symbols length (i.e., T = 400). The number of scatterers is set to be L = 2, 4 and 6, respectively. All the results are obtained at = . It can be observed that the NMSE performance of the proposed S-ADMM scheme is getting worse as the number of scatterers are increasing. The same thing happened in the case of high training symbols length (i.e., T = 1200). Figure 5b also indicates the same results that as the number of scatterers are increasing the NMSE performance is getting worse. This happens because of the worse scattering nature of mmWaves. Figure 5c depicts the effects of escalation in path of mmWaves. Therefore, to summarize, by the inherent nature of mmWave, it can be said that the performance of a mmWave MIMO system decreases as the number of propagation paths and scatterers increases, but still the performance of the proposed S-ADMM is much better than the OMP, VAMP, GAMP-GM, BOMP and the Ex-ADMM as depicted in Figure 5c.
5. Concluding Remarks
To jointly optimize the low rank and sparsity-based problem for the channel estimation of a mmWave MIMO system, a symmetrical version of ADMM (S-ADMM) has been proposed. The S-ADMM treated every variable symmetrically in the optimization problem. For better convergence rate, to enhance the step size, a relaxation parameter is multiplied into the step size of duals. In order to get better optimal solutions, the proposed scheme divides the optimization problems into several subproblems and solves them individually. Although, S-ADMM is better for recovering the training symbols, the performance is degraded when the number of scatterers and paths are increased. Therefore, there is room for improvement. With proper modifications, the proposed S-ADMM algorithm can be further extended for the estimation of time-varying mmWave channels in a hybrid MIMO system. Extensive simulations experiments are carried out to explain the validation and superiority of the scheme. Comprehensively, the proposed S-ADMM scheme performed better than all other state-of-art benchmark algorithms considered in this work.
Author Contributions
Conceptualization, P.S.S.; methodology, P.S.S.; validation, P.S.S., L.C., writing, review and editing, L.C., A.H.W. and P.S.S.; funding acquisition, L.C.; supervision, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Science and Technology Major Project (NSTMP) under grant 2018ZX03001006-002.
Acknowledgments
The first author, P.S.S., hereby acknowledges the University of the Chinese Academy of Sciences (CAS) and the World Academy of Sciences (TWAS) for financial support for studies under the CAS-TWAS Fellowship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications Above 100 GHz: Opportunities and Challenges for 6G and Beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Cheng, X.; Tang, C.; Zhang, Z. Accurate Channel Estimation for Millimeter-Wave MIMO Systems. IEEE Trans. Veh. Technol. 2019, 68, 5159–5163. [Google Scholar] [CrossRef]
- Cao, Z.; Geng, H.; Chen, Z.; Chen, P. Sparse-Based Millimeter Wave Channel Estimation with Mutual Coupling Effect. Electron 2019, 8, 358. [Google Scholar] [CrossRef]
- Darsena, D.; Gelli, G.; Verde, F. Beamforming and Precoding Techniques. Wiley 5G Ref. 2020, 1–29. [Google Scholar] [CrossRef]
- Manoj, A.; Kannu, A.P. Channel Estimation Strategies for Multi-User mm Wave Systems. IEEE Trans. Commun. 2018, 66, 5678–5690. [Google Scholar] [CrossRef]
- El Ayach, O.; Rajagopal, S.; Abu-Surra, S.; Pi, Z.; Heath, R.W. Spatially Sparse Precoding in Millimeter Wave MIMO Systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Roh, W.; Seol, J.-Y.; Lee, B.; Kim, Y.; Cheun, K.; Aryanfar, F.; Park, J.; Lee, J.; Cho, J. Millimeter-Wave Beamforming as an Enabling Technology for 5G Cellular Communications: Theoretical Feasibility and Prototype Results. IEEE Commun. Mag. 2014, 52, 106–113. [Google Scholar] [CrossRef]
- Mo, J.; Schniter, P.; Prelcic, N.G.; Heath, R.W. Channel Estimation in Millimeter Wave MIMO Systems with One-Bit Quantization. In Proceedings of the 2014 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 957–961. [Google Scholar]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Single-Sided Adaptive Estimation of Multi-Path Millimeter Wave Channels. In Proceedings of the 2014 IEEE 15th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Toronto, ON, Canada, 22–25 June 2014; pp. 125–129. [Google Scholar]
- Payami, S.; Shariat, M.; Ghoraishi, M.; Dianati, M. Effective RF Codebook Design and Channel Estimation for Millimeter Wave Communication Systems. In Proceedings of the 2015 IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 1226–1231. [Google Scholar]
- Yang, J.; Wei, Z.; Li, N.; Sang, L.; Li, P. Enhanced Multi-Resolution Hierarchical Codebook Design for Adaptive Compressed Sensing Based Millimeter Wave Channel Estimation. In Proceedings of the 2016 IEEE/CIC International Conference on Communications in China (ICCC), Chengdu, China, 27–29 July 2016; pp. 1–5. [Google Scholar]
- Li, X.; Fang, J.; Li, H.; Wang, P. Millimeter Wave Channel Estimation via Exploiting Joint Sparse and Low-Rank Structures. IEEE Trans. Wirel. Commun. 2018, 17, 1123–1133. [Google Scholar] [CrossRef]
- Lee, J.; Gil, G.-T.; Lee, Y.H. Channel Estimation via Orthogonal Matching Pursuit for Hybrid MIMO Systems in Millimeter Wave Communications. IEEE Trans. Commun. 2016, 64, 2370–2386. [Google Scholar] [CrossRef]
- Ghauch, H.; Kim, T.-J.; Bengtsson, M.; Skoglund, M. Subspace Estimation and Decomposition for Large Millimeter-Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 528–542. [Google Scholar] [CrossRef]
- Wang, M.; Gao, F.; Shlezinger, N.; Flanagan, M.F.; Eldar, Y.C. A Block Sparsity Based Estimator for mmWave Massive MIMO Channels wWith Beam Squint. IEEE Trans. Signal Process. 2019, 68, 49–64. [Google Scholar] [CrossRef]
- Vlachos, E.; Alexandropoulos, G.C.; Thompson, J.S.; Alexandropoulus, G. Wideband MIMO Channel Estimation for Hybrid Beamforming Millimeter Wave Systems via Random Spatial Sampling. IEEE J. Sel. Top. Signal Process. 2019, 13, 1136–1150. [Google Scholar] [CrossRef]
- Venugopal, K.; Alkhateeb, A.; Heath, R.W.; Prelcic, N.G. Time-Domain Channel Estimation for Wideband Millimeter Wave Systems with Hybrid Architecture. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 6493–6497. [Google Scholar]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel Estimation and Hybrid Precoding for Millimeter Wave Cellular Systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Mendez-Rial, R.; Rusu, C.; Alkhateeb, A.; González-Prelcic, N.; Heath, R.W. Channel Estimation and Hybrid Combining for mmWave: Phase Shifters or Switches? In Proceedings of the 2015 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 1–6 February 2015; pp. 90–97. [Google Scholar]
- Alexandropoulos, G.C.; Chouvardas, S. Low Complexity Channel Estimation for Millimeter Wave Systems with Hybrid A/D Antenna Processing. In Proceedings of the 2016 IEEE Globecom Workshops, Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Venugopal, K.; Alkhateeb, A.; Gonzalez-Prelcic, N.; Heath, R.W. Channel Estimation for Hybrid Architecture-Based Wideband Millimeter Wave Systems. IEEE J. Sel. Areas Commun. 2017, 35, 1996–2009. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C. Position Aided Beam Alignment for Millimeter Wave Backhaul Systems with Large Phased Arrays. In Proceedings of the 2017 IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Curacao, The Netherlands, 10–13 December 2017; pp. 1–5. [Google Scholar]
- Cai, T.T.; Wang, L. Orthogonal Matching Pursuit for Sparse Signal Recovery with Noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Xie, H.; Gao, F.; Zhang, S.; Jin, S. A Unified Transmission Strategy for TDD/FDD Massive MIMO Systems with Spatial Basis Expansion Model. IEEE Trans. Veh. Technol. 2017, 66, 3170–3184. [Google Scholar] [CrossRef]
- Adhikary, A.; Al Safadi, E.; Samimi, M.K.; Wang, R.; Caire, G.; Rappaport, T.S.; Molisch, A.F. Joint Spatial Division and Multiplexing for mm-Wave Channels. IEEE J. Sel. Areas Commun. 2014, 32, 1239–1255. [Google Scholar] [CrossRef]
- Nguyen, S.L.H.; Ghrayeb, A. Compressive Sensing-Based Channel Estimation for Massive Multiuser MIMO Systems. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2890–2895. [Google Scholar]
- Rao, X.; Lau, V.K.N. Distributed Compressive CSIT Estimation and Feedback for FDD Multi-User Massive MIMO Systems. IEEE Trans. Signal Process. 2014, 62, 3261–3271. [Google Scholar] [CrossRef]
- Wang, M.; Gao, F.; Jin, S.; Lin, H. An Overview of Enhanced Massive MIMO With Array Signal Processing Techniques. IEEE J. Sel. Top. Signal Process. 2019, 13, 886–901. [Google Scholar] [CrossRef]
- Boyd, S. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. In Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Now Publishers Inc.: Breda, The Netherlands, 2010; Volume 3, pp. 1–122. [Google Scholar]
- Wang, J.; Yu, F.; Chen, X.; Zhao, L. ADMM for Efficient Deep Learning with Global Convergence. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 111–119. [Google Scholar]
- Chan, S.H.; Wang, X.; Elgendy, O.A. Plug-and-Play ADMM for Image Restoration: Fixed-Point Convergence and Applications. IEEE Trans. Comput. Imaging 2016, 3, 84–98. [Google Scholar] [CrossRef]
- Bai, J.; Liang, J.; Guo, K.; Jing, Y. Accelerated Symmetric ADMM and Its Applications in Signal Processing. arXiv 2019, arXiv:1906.12015. [Google Scholar]
- Vlachos, E.; Alexandropoulos, G.C.; Thompson, J.S. Massive MIMO Channel Estimation for Millimeter Wave Systems via Matrix Completion. IEEE Signal Process. Lett. 2018, 25, 1675–1679. [Google Scholar] [CrossRef]
- Srivastav, P.S.; Chen, L.; Wahla, A.H.; Srivastav, P.; Srivastav, P. Precise Channel Estimation Approach for a mmWave MIMO System. Appl. Sci. 2020, 10, 4397. [Google Scholar] [CrossRef]
- He, B.; Ma, F.; Yuan, X. Convergence Study on the Symmetric Version of ADMM with Larger Step Sizes. SIAM J. Imaging Sci. 2016, 9, 1467–1501. [Google Scholar] [CrossRef]
- He, B.; Liu, H.; Wang, Z.; Yuan, X. A Strictly Contractive Peaceman--Rachford Splitting Method for Convex Programming. SIAM J. Optim. 2014, 24, 1011–1040. [Google Scholar] [CrossRef]
- Rangan, S.; Schniter, P.; Fletcher, A.K. Vector Approximate Message Passing. IEEE Trans. Inf. Theory 2019, 65, 6664–6684. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kuppinger, P.; Bolcskei, H. Block-Sparse Signals: Uncertainty Relations and Efficient Recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef]
- Rangan, S. Generalized Approximate Message Passing for Estimation with Random Linear Mixing. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; pp. 2168–2172. [Google Scholar]
- Ma, Y.; Zhu, J.; Baron, D. Approximate Message Passing Algorithm with Universal Denoising and Gaussian Mixture Learning. IEEE Trans. Signal Process. 2016, 64, 5611–5622. [Google Scholar] [CrossRef]
- Cai, J.-F.; Candés, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Torkildson, E.; Madhow, U.; Rodwell, M. Indoor Millimeter Wave MIMO: Feasibility and Performance. IEEE Trans. Wirel. Commun. 2011, 10, 4150–4160. [Google Scholar] [CrossRef]
- Akoum, S.; El Ayach, O.; Heath, R.W. Coverage and Capacity in Mmwave Cellular Systems. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 4–7 November 2012; pp. 688–692. [Google Scholar]
- Smolders, A.B.; Reniers, A.C.F.; Johannsen, U.; Herben, M.H.A.J. Measurement and Calibration Challenges of Microwave and Millimeter-Wave Phased-Arrays. In Proceedings of the 2013 International Workshop on Antenna Technology (iWAT), Karlsruhe, Germany, 4–6 March 2013; pp. 358–361. [Google Scholar]
- Forenza, A.; Love, D.; Heath, R.W. Simplified Spatial Correlation Models for Clustered MIMO Channels with Different Array Configurations. IEEE Trans. Veh. Technol. 2007, 56, 1924–1934. [Google Scholar] [CrossRef]
- Sayeed, A. Deconstructing multiantenna fading channels. IEEE Trans. Signal Process. 2002, 50, 2563–2579. [Google Scholar] [CrossRef]
- Brady, J.; Behdad, N.; Sayeed, A.M. Beamspace MIMO for Millimeter-Wave Communications: System Architecture, Modeling, Analysis, and Measurements. IEEE Trans. Antennas Propag. 2013, 61, 3814–3827. [Google Scholar] [CrossRef]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix Completion From a Few Entries. IEEE Trans. Inf. Theory 2010, 56, 2980–2998. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Glowinski, R. Numerical Methods for Nonlinear Variational Problems; Tata Institute of Fundamental Research: Mumbai, Maharashtra, India, 1980. [Google Scholar]
- Chen, C.; He, B.; Yuan, X. Matrix completion via an alternating direction method. Ima J. Numer. Anal. 2011, 32, 227–245. [Google Scholar] [CrossRef]
- He, B.; Xu, M.; Yuan, X. Solving large-scale least squares covariance matrix problems by alternating direction methods. SIAM J. Matrix Anal. Appl. 2011, 32, 136. [Google Scholar] [CrossRef]
- Eckstein, J.; Yao, W. Understanding the convergence of the alternating direction method of multipliers: Theoretical and computational perspectives. Pac. J. Optim. 2015, 11, 619–644. [Google Scholar]
- Eckstein, J.; Bertsekas, D.P. On the Douglas—Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992, 55, 293–318. [Google Scholar] [CrossRef]
- Gabay, D. Chapter IX Applications of the Method of Multipliers to Variational Inequalities. In Mathematical Models in Environmental Problems; Elsevier: Amsterdam, The Netherlands, 1983; Volume 15, pp. 299–331. [Google Scholar]
- Douglas, J.; Rachford, H.H. On the numerical solution of heat conduction problems in two and three space variables. Trans. Am. Math. Soc. 1956, 82, 421–439. [Google Scholar] [CrossRef]
- Lions, P.L.; Mercier, B. Splitting Algorithms for the Sum of Two Nonlinear Operators. SIAM J. Numer. Anal. 1979, 16, 964–979. [Google Scholar] [CrossRef]
- Peaceman, D.W.; Rachford, J.H.H. The Numerical Solution of Parabolic and Elliptic Differential Equations. J. Soc. Ind. Appl. Math. 1955, 3, 28–41. [Google Scholar] [CrossRef]
- Ma, F.; Ni, M.; Zhang, X.; Yu, Z. Solving Lasso: Extended ADMM is more efficient than ADMM. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 55–58. [Google Scholar] [CrossRef]
- Chiang, K.-Y.; Hsieh, C.-J.; Dhillon, I.S. Matrix Completion with Noisy Side Information. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 3447–3455. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Van Der Vorst, H.A. Iterative Krylov Methods for Large Linear Systems; Cambridge University Press: Cambridge, UK, 2003; Volume 13. [Google Scholar]
- Bucklew, J.; Radeke, R. On the monte carlo simulation of digital communication systems in gaussian noise. IEEE Trans. Commun. 2003, 51, 267–274. [Google Scholar] [CrossRef]
- Berriche, L.; Abed-Meraim, K.; Belfiore, J. Investigation of the Channel Estimation Error on MIMO System Performance. In Proceedings of the 2005 13th European Signal Processing Conference, Antalya, Turkey, 4–8 September 2005; pp. 1–4. [Google Scholar]
- Yoo, T.; Goldsmith, A. Capacity and power allocation for fading MIMO channels with channel estimation error. IEEE Trans. Inf. Theory 2006, 52, 2203–2214. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).