On Entropy of Probability Integral Transformed Time Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Probability Integral Transform, Sklar’s Theorem and Copula Density
2.2. XEn, ApEn and SampEn
- Reference series xi ∈ X, i = 1, …, N;
- Follower series yj ∈ Y, j = 1, …, N.
- Template vector ;
- Follower vector ;
- .
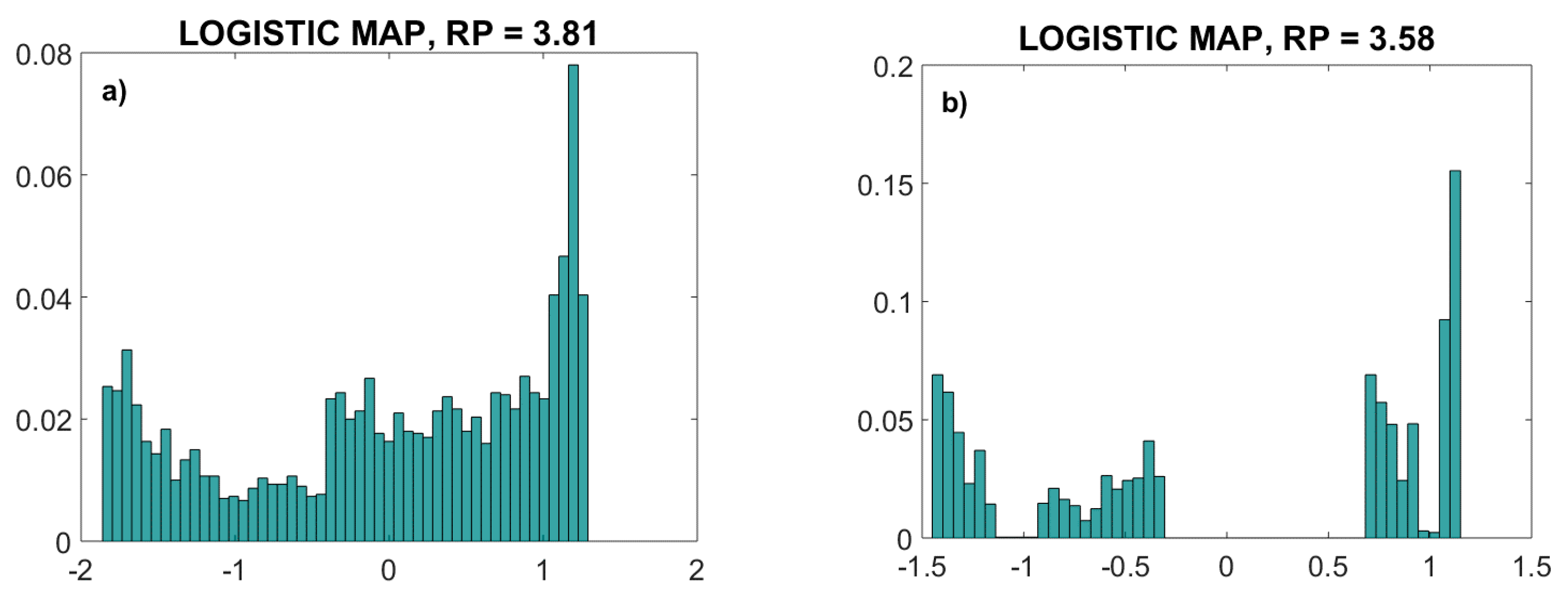
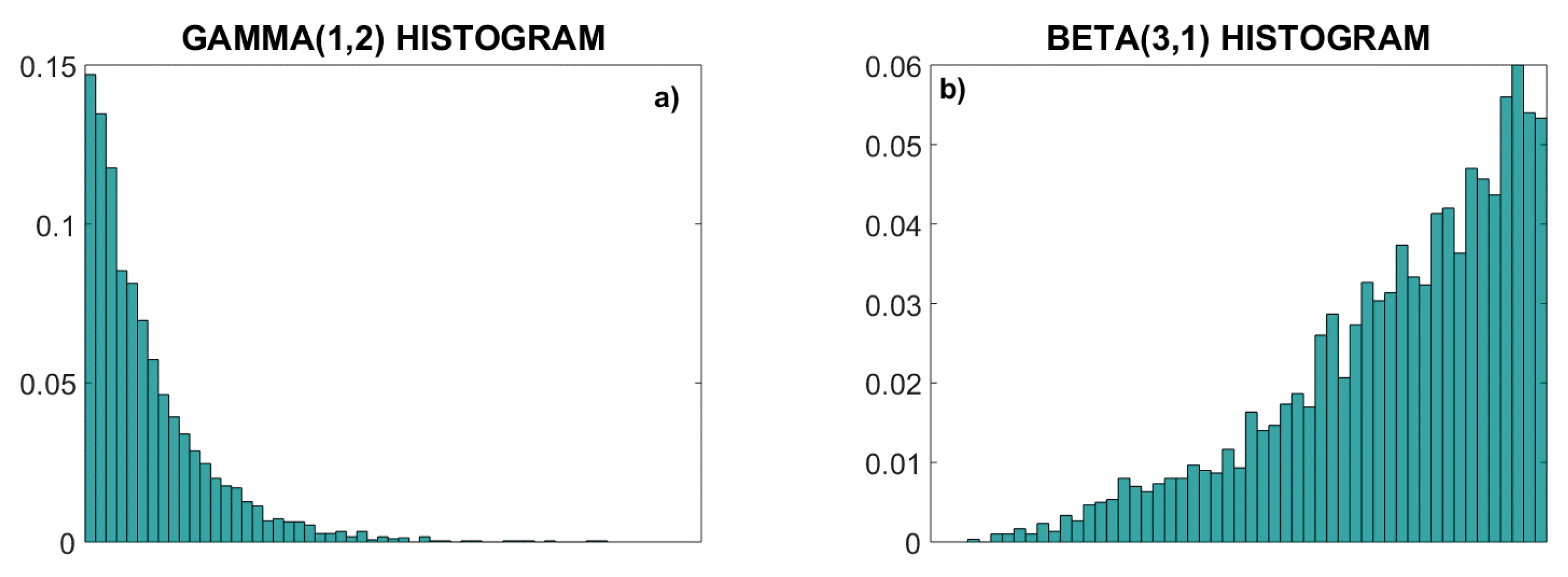
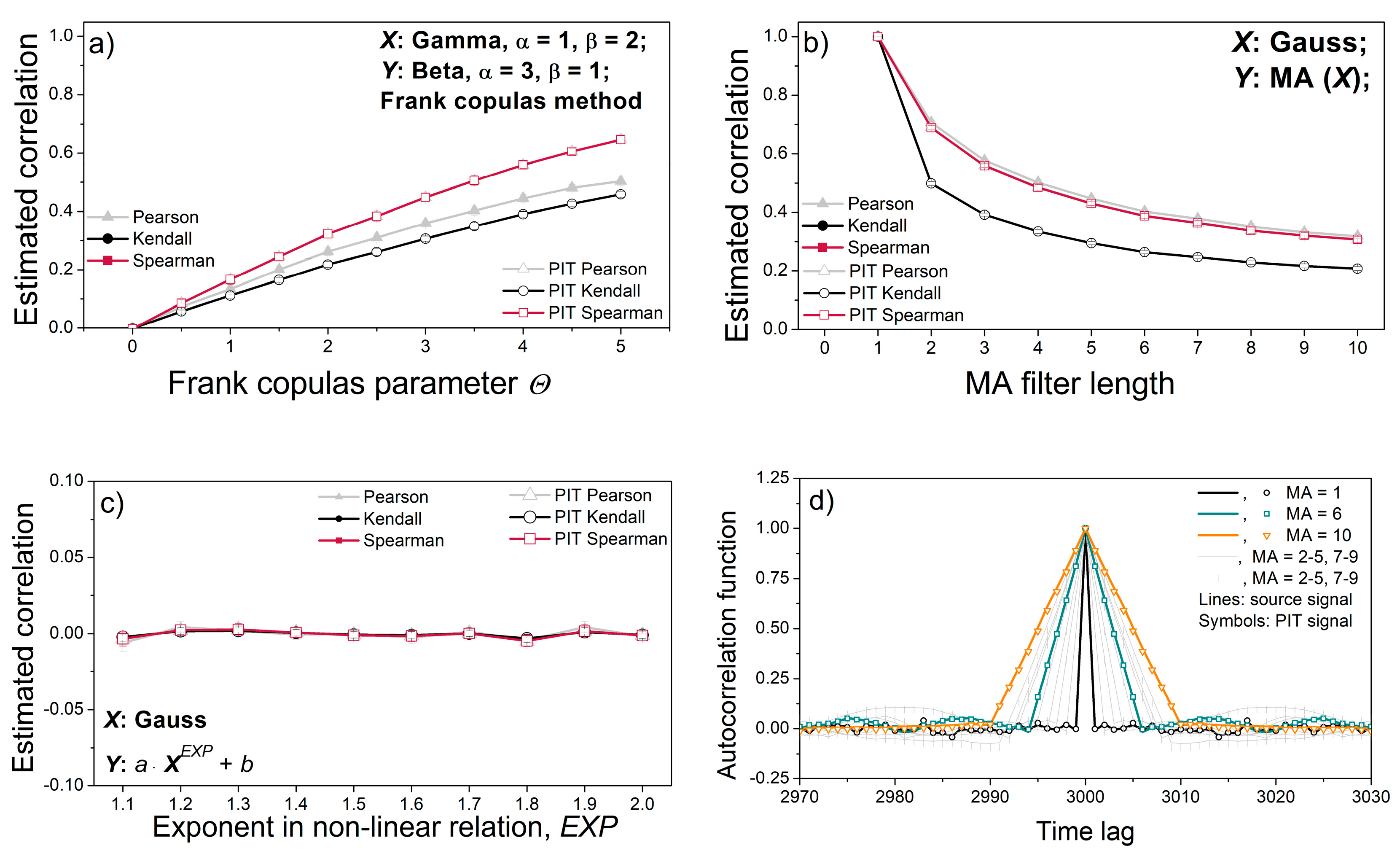
2.3. Artificial Time Series
2.4. Time Series Recorded from the Laboratory Rats Exposed to Shaker and Restraint Stress
3. Results and Discussion
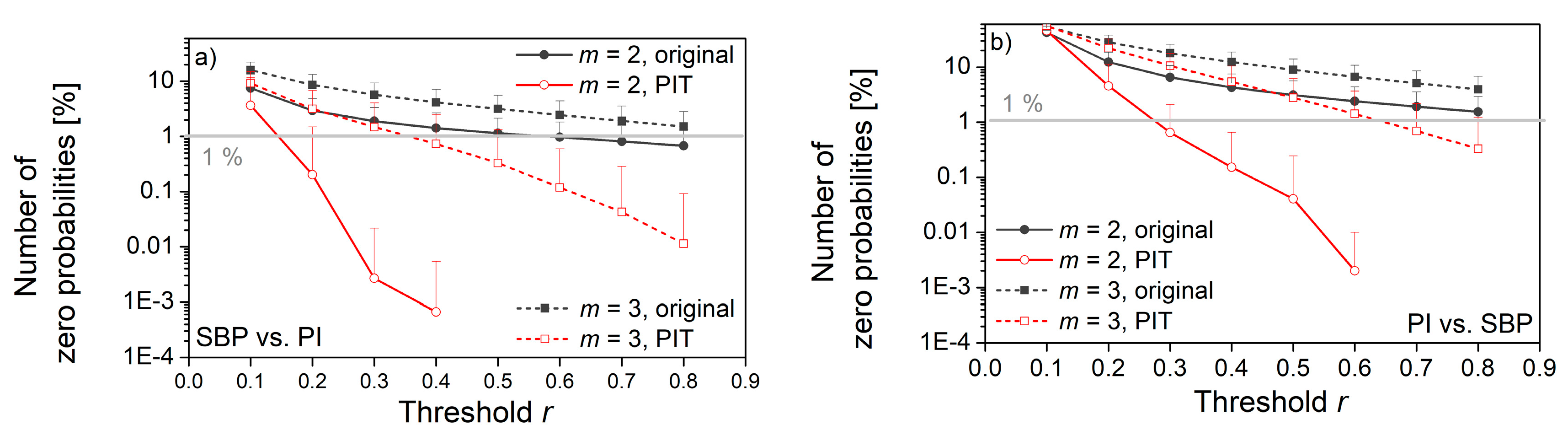
3.1. Threshold Choice
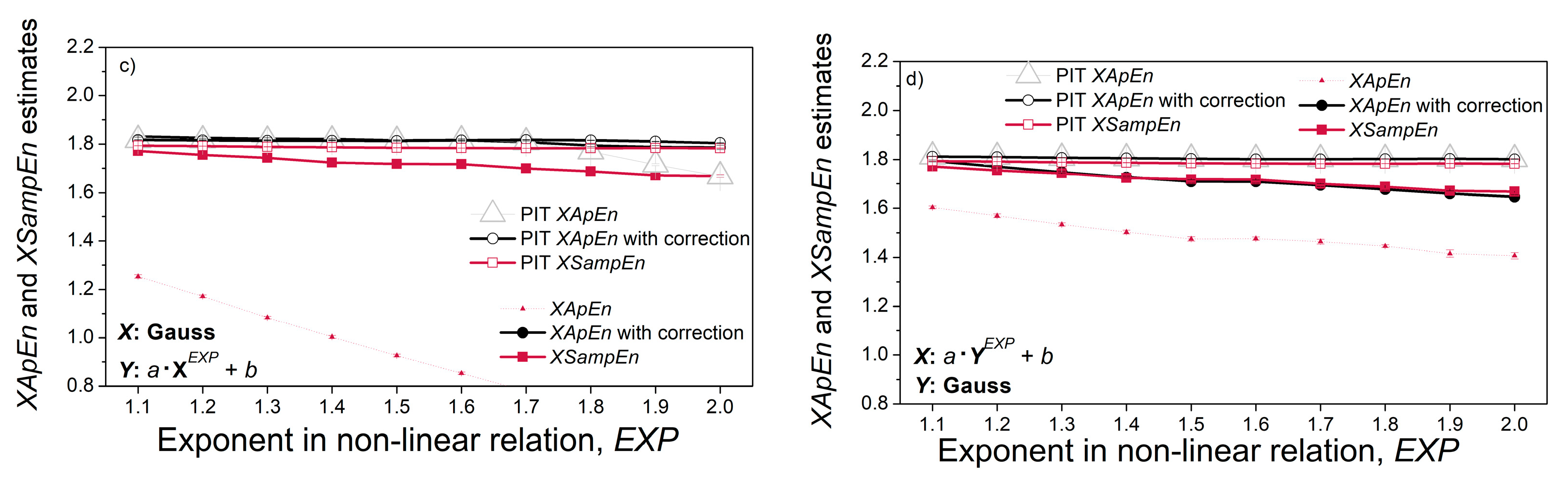
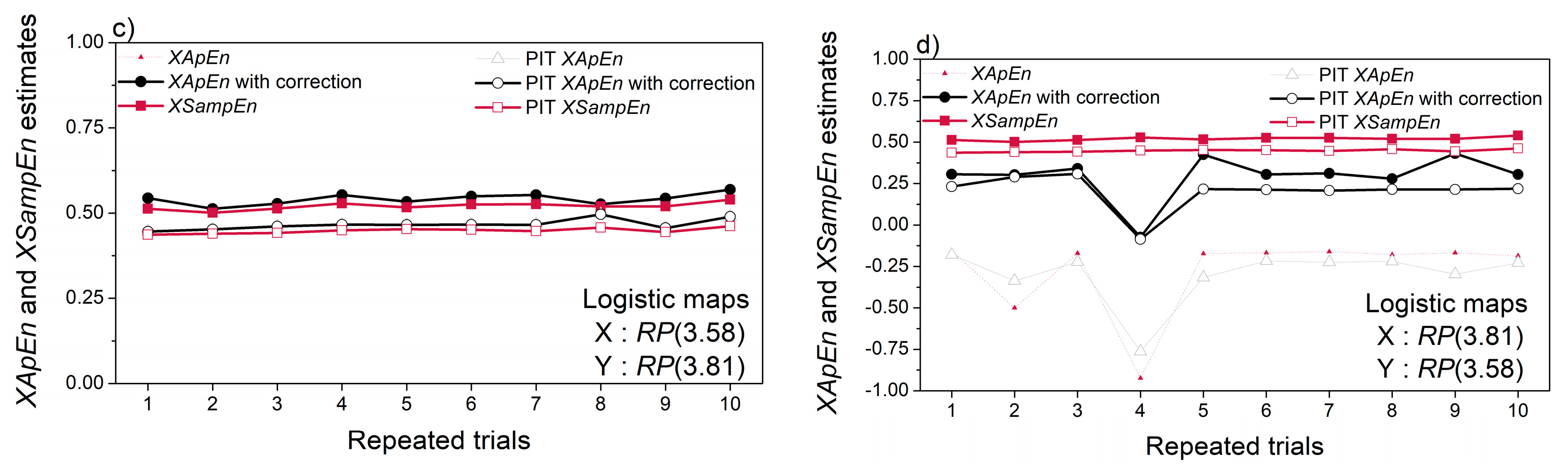
3.2. Entropy Estimated from Artificial Data
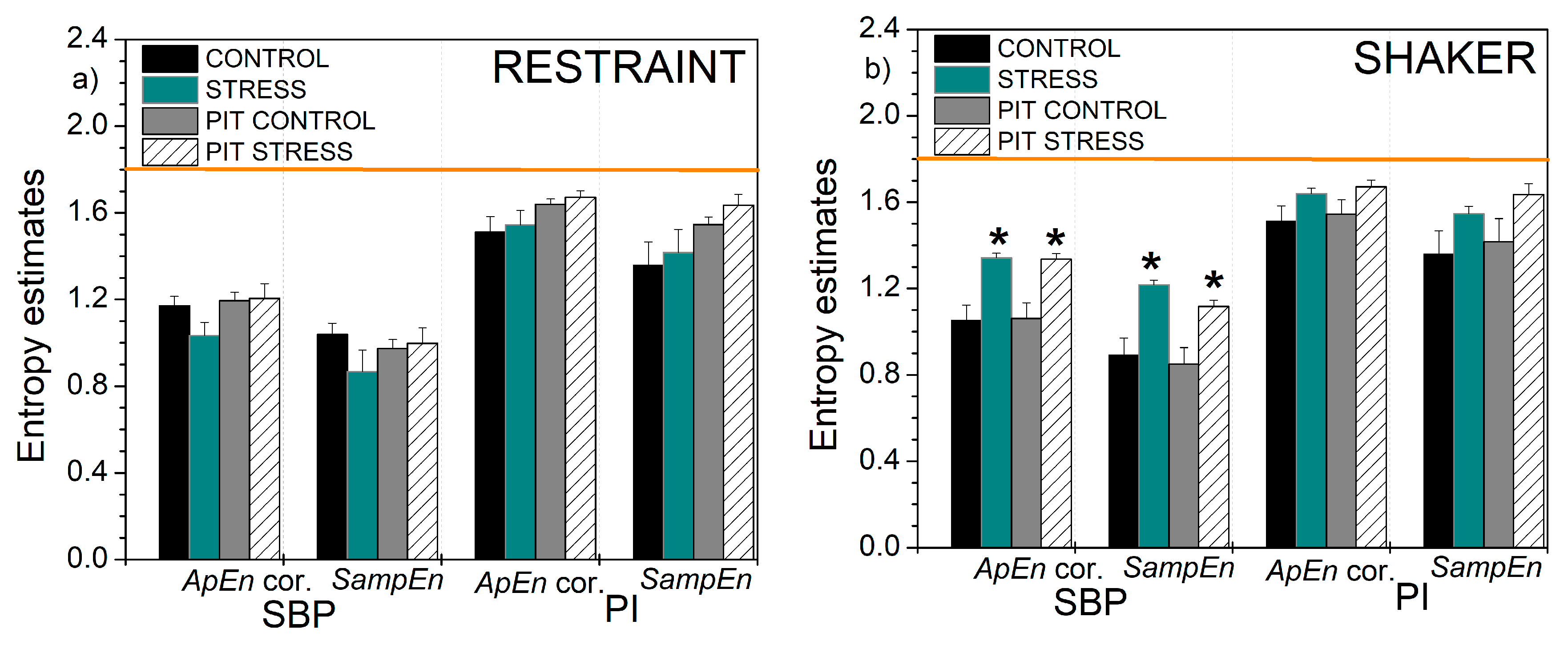
3.3. Entropy Estimated from Cardiovascular Signals of Laboratory Rats Exposed to Stress
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Shannon, C.E. Communications in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Gustavo, D.; Bernd, S. Information Dynamics: Foundations and Applications, 1st ed.; Springer: New York, NY, USA, 2012; p. 101. ISBN 978-1-4613-0127-1. [Google Scholar]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef] [Green Version]
- Eckmann, J.-P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time−series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [Green Version]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Cornforth, D.J.; Khandoker, A.H. ECG Time Series Variability Analysis: Engineering and Medicine, 1st ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017; pp. 1–450. ISBN 978-1482243475. [Google Scholar]
- Li, X.; Yu, S.; Chen, H.; Lu, C.; Zhang, K.; Li, F. Cardiovascular autonomic function analysis using approximate entropy from 24-h heart rate variability and its frequency components in patients with type 2 diabetes. J. Diabetes Investig. 2015, 6, 227–235. [Google Scholar] [CrossRef] [Green Version]
- Krstacic, G.; Gamberger, D.; Krstacic, A.; Smuc, T.; Milicic, D. The chaos theory and non-linear dynamics in heart rate variability in patients with heart failure. In Proceedings of the Computers in Cardiology, Bologna, Italy, 14–17 September 2008; pp. 957–959. [Google Scholar] [CrossRef]
- Storella, R.J.; Wood, H.W.; Mills, K.M.; Kanters, J.K.; Højgaard, M.V.; Holstein-Rathlou, N.-H. Approximate entropy and point correlation dimension of heart rate variability in healthy subjects. Integr. Psychol. Behav. Sci. 1998, 33, 315–320. [Google Scholar] [CrossRef]
- Tulppo, M.P.; Makikallio, T.H.; Takala, T.E.; Seppanen, T.; Huikuri, H.V. Quantitative beat-to-beat analysis of heart rate dynamics during exercise. Am. J. Physiol. Heart Circ. Physiol. 1996, 271, H244–H252. [Google Scholar] [CrossRef]
- Boskovic, A.; Loncar-Turukalo, T.; Sarenac, O.; Japundžić-Žigon, N.; Bajić, D. Unbiased entropy estimates in stress: A parameter study. Comput. Biol. Med. 2012, 42, 667–679. [Google Scholar] [CrossRef] [PubMed]
- Ryan, S.M.; Goldberger, A.L.; Pincus, S.M.; Mietus, J.; Lipsitz, L.A. Gender- and age-related differences in heart rate dynamics: Are women more complex than men? J. Am. Coll. Cardiol. 1994, 24, 1700–1707. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.Y.; Zhang, L.F.; Wang, X.B.; Cheng, J.H. Age dependency and correlation of heart rate variability, blood pressure variability and baroreflex sensitivity. J. Gravit. Physiol. 2000, 7, 145–146. [Google Scholar]
- Sunkaria, R.K. The deterministic chaos in heart rate variability signal and analysis techniques. Int. J. Comput. Appl. 2011, 35, 39–46. [Google Scholar] [CrossRef]
- Marwaha, P.; Sunkaria, R.K. Cardiac variability time-series analysis by sample entropy and multiscale entropy. Int. J. Med. Eng. Inform. 2015, 7, 1–14. [Google Scholar] [CrossRef]
- Chen, C.; Jin, Y.; Lo, I.L.; Zhao, H.; Sun, B.; Zhao, Q.; Zhang, X.D. Complexity change in cardiovascular disease. Int. J. Biol. Sci. 2017, 13, 1320–1328. [Google Scholar] [CrossRef]
- Papaioannou, V.; Giannakou, M.; Maglaveras, N.; Sofianos, E.; Giala, M. Investigation of heart rate and blood pressure variability, baroreflex sensitivity, and approximate entropy in acute brain injury patients. J. Crit. Care 2008, 23, 380–386. [Google Scholar] [CrossRef]
- Pincus, S.M.; Mulligan, T.; Iranmanesh, A.; Gheorghiu, S.; Godschalk, M.; Veldhuis, J.D. Older males secrete lutenizing hormone and testosterone more irregularly, and jointly more asynchronously than younger males. Proc. Natl. Acad. Sci. USA 1996, 93, 14100–14105. [Google Scholar] [CrossRef] [Green Version]
- Skoric, T.; Sarenac, O.; Milovanovic, B.; Japundzic-Zigon, N.; Bajic, D. On consistency of cross-approximate entropy in cardiovascular and artificial environments. Complexity 2017, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.-K.; Chien, Y.-H. Performance evaluation of an entropy-based structural health monitoring system utilizing composite multiscale cross-sample entropy. Entropy 2019, 21, 41. [Google Scholar] [CrossRef] [Green Version]
- Castiglioni, P.; Parati, G.; Faini, A. Information-domain analysis of cardiovascular complexity: Night and day modulations of entropy and the effects of hypertension. Entropy 2019, 21, 550. [Google Scholar] [CrossRef] [Green Version]
- Chon, K.H.; Scully, C.G.; Lu, S. Approximate entropy for all signals. IEEE Eng. Med. Biol. Mag. 2009, 28, 18–23. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Chen, X.; Kanters, J.K.; Solomon, I.C.; Chon, K.H. Automatic selection of the threshold value r for approximate entropy. IEEE Trans. Biomed. Eng. 2008, 55, 1966–1972. [Google Scholar] [CrossRef] [PubMed]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A. The effect of time delay on approximate and sample entropy calculations. Physica D 2008, 237, 3069–3074. [Google Scholar] [CrossRef]
- Porta, A.; Baselli, G.; Liberati, D.; Montano, N.; Cogliati, C.; Gnecchi-Ruscone, T.; Malliani, A.; Cerutti, S. Measuring regularity by means of a correctesconditional entropy in sympathetic outflow. Biol. Cybern. 1998, 78, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Szczesna, A. Quaternion entropy for analysis of gait data. Entropy 2019, 21, 79. [Google Scholar] [CrossRef] [Green Version]
- Behrendt, S.; Dimpfl, T.; Peter, F.J.; Zimmermann, D.J. RTransferEntropy—Quantifying information flow between different time series using effective transfer entropy. SoftwareX 2019, 10, 100265. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Marshak, A. Approximate entropy and sample entropy: A comprehensive tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef] [Green Version]
- Jovanovic, S.; Skoric, T.; Sarenac, O.; Milutinovic-Smiljanic, S.; Japundzic-Zigon, N.; Bajic, D. Copula as a dynamic measure of cardiovascular signal interactions. Biomed. Signal Process Control 2018, 43, 250–264. [Google Scholar] [CrossRef]
- Embrechts, P.; Hofert, M. A note on generalized inverses. Math. Methods Oper. Res. 2013, 77, 423–432. [Google Scholar] [CrossRef] [Green Version]
- May, R. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Pappoulis, A.; Pillai, U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2002; p. 139. [Google Scholar]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. del’Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Aas, K.; Czado, C.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C.; Egan, M.; Clavier, L.; Peters, G.; Gorce, J.-M. Copula-based interference models for IoT wireless networks. In Proceedings of the ICC 2019—53rd IEEE International Conference on Communications, Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, S.C.; Liu, T.J.; Hong, H.P. Reliability of tower and tower-line systems under spatiotemporally varying wind or earthquake loads. J. Struct. Eng. 2017, 143, 04017137. [Google Scholar] [CrossRef]
- Modiri, S.; Belda, S.; Hoseini, M.; Heinkelmann, R.; Ferrándiz, J.M.; Schuh, H. A new hybrid method to improve the ultra-short-term prediction of LOD. J. Geod. 2020, 94, 1. [Google Scholar] [CrossRef] [Green Version]
- Lazoglou, G.; Anagnostopoulou, C. Joint distribution of temperature and precipitation in the Mediterranean, using the Copula method. Theor. Appl. Climatol. 2019, 135, 1399–1411. [Google Scholar] [CrossRef]
- Iyengar, S.G.; Dauwels, J.; Varshney, P.K.; Cichocki, A. Quantifying EEG synchrony using copulas. Proc. IEEE Int. Conf. Acoust. Speech Signal Process. 2010, 505–508. [Google Scholar] [CrossRef]
- Wu, H.-T.; Lee, C.-Y.; Liu, C.-C.; Liu, A.-B. Multiscale Cross-Approximate Entropy Analysis as a Measurement of Complexity between ECG R-R Interval and PPG Pulse Amplitude Series among the Normal and Diabetic Subjects. Comput. Math. Methods Med. 2013, 2013, 231762. [Google Scholar] [CrossRef]
- Tarvainen, M.P.; Ranta-aho, P.O.; Karjalainen, P.A. An advanced detrending approach with application to HRV analysis. IEEE Trans. Biomed. Eng. 2002, 42, 172–174. [Google Scholar] [CrossRef] [PubMed]
- Hao, Z.; Singh, V.P. Entropy-copula method for single-site monthly streamflow simulation. Water Resour. Res. 2012, 48, 1–8. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Z. Mutual information is copula entropy. Tsinghua Sci. Technol. 2011, 16, 51–54. [Google Scholar] [CrossRef]
- Ince, R.A.A.; Giordano, B.L.; Kayser, C.; Rousselet, G.A.; Gross, J.; Schyns, P.G. A statistical framework for neuroimaging data analysis based on mutual information estimated via a gaussian copula. Hum. Brain Mapp. 2017, 38, 1541–1573. [Google Scholar] [CrossRef] [PubMed]
- Blaber, A.P.; Yamamoto, Y.; Hughson, R.L. Methodology of spontaneous baroreflex relationship assessed by surrogate data analysis. Am. J. Physiol. Heart Circ. Physiol. 1995, 268, H1682–H1687. [Google Scholar] [CrossRef] [PubMed]
- Skoric, T.; Mohamoud, O.; Milovanovic, B.; Japundzic-Zigon, N.; Bajic, D. Binarized cross-approximate entropy in crowdsensing environment. Comput. Biol. Med. 2017, 80, 137–147. [Google Scholar] [CrossRef]
- Agresti, A. Analysis of Ordinal Categorical Data, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2010; ISBN 978-0-470-08289-8. [Google Scholar]
- Nguyen, F.; Laval, J.-P.; Kestener, P.; Cheskidov, A.; Shvydkoy, R.; Dubrulle, B. Local estimates of Hölder exponents in turbulent vector fields. Phys. Rev. E 2019, 99, 053114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarenac, O.; Lozic, M.; Drakulic, S.; Bajic, D.; Paton, J.F.; Murphy, D.; Japundzic-Zigon, N. Autonomic mechanisms underpinning the stress response in borderline hypertensive rats. Exp. Physiol. 2011, 96, 574–589. [Google Scholar] [CrossRef] [Green Version]
- Wessel, N.; Malberg, H.; Bauernschmitt, R.; Kurths, J. Nonlinear methods of cardiovascular physics and their clinical applicability. Int. J. Bifurc. Chaos 2007, 17, 3325–3371. [Google Scholar] [CrossRef] [Green Version]
- Carvajal, R.; Żebrowski, J.J.; Vallverdu, M.; Baranowski, R.; Chojnowska, L.; Poplawska, W.; Caminal, P. Dimensional analysis of HRV in hypertrophic cardiomyopathy patients. IEEE Eng. Med. Biol. Mag. 2002, 21, 71–78. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data Analysis and Measurement Procedures; Wiley Series in Probability and Statistics; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Jeruchim, M.C. Techniques for estimating the bit error rate in the simulation of digital communication systems. IEEE J. Sel. Areas Commun. 1984, 2, 153–170. [Google Scholar] [CrossRef]











| SBP [mmHg] | PI [ms] | |||
|---|---|---|---|---|
| STRESS | BASELINE | STRESS | BASELINE | STRESS |
| SHAKER | 116.28 ± 6.82 | 125.55 ± 8.89 | 167.8 ± 13.95 | 157.97 ± 10.98 |
| RESTRAINT | 107.08 ± 7.83 | 114.37 ± 24.92 | 179.29 ± 13.66 | 131.46 ± 5.71 * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajić, D.; Mišić, N.; Škorić, T.; Japundžić-Žigon, N.; Milovanović, M. On Entropy of Probability Integral Transformed Time Series. Entropy 2020, 22, 1146. https://doi.org/10.3390/e22101146
Bajić D, Mišić N, Škorić T, Japundžić-Žigon N, Milovanović M. On Entropy of Probability Integral Transformed Time Series. Entropy. 2020; 22(10):1146. https://doi.org/10.3390/e22101146
Chicago/Turabian StyleBajić, Dragana, Nataša Mišić, Tamara Škorić, Nina Japundžić-Žigon, and Miloš Milovanović. 2020. "On Entropy of Probability Integral Transformed Time Series" Entropy 22, no. 10: 1146. https://doi.org/10.3390/e22101146
APA StyleBajić, D., Mišić, N., Škorić, T., Japundžić-Žigon, N., & Milovanović, M. (2020). On Entropy of Probability Integral Transformed Time Series. Entropy, 22(10), 1146. https://doi.org/10.3390/e22101146






