1. Introduction
This paper presents a new and novel method for the segmentation and dimension reduction in high dimensional time-series data. We develop hybrid modeling between mixture-model cluster analysis and sparse principal components regression (MIX-SPCR) model as an expert unsupervised classification methodology with information complexity () criterion as the fitness function. This new approach performs dimension reduction in high dimensional time-series data and, at the same time, determines the number of component clusters.
The research of time-series segmentation and change point positioning has been a hot topic of research for a long time. Different research groups have provided solutions with various approaches in this area, including, but not limited to, Bayesian methods Barber et al. [
1], fuzzy systems Abonyi and Feil [
2], and complex system modeling Spagnolo and Valenti [
3], Valenti et al. [
4], S Lima [
5], Ding et al. [
6]. We group these approaches into two branches, one based on complex systems modeling and the other on the statistical model through parameter estimation and inference. Among the complex systems-based modeling approaches, it is worth noting a series of papers that use the stochastic volatility model by Spagnolo and Valenti [
3]. For example, these authors used a nonlinear Hestone model to analyze 1071 stocks on the New York Stock Exchange (1987–1998). After accounting for the stochastic nature of volatility, the model is well suited to extracting the escape time distribution from financial time-series data. The authors also identified the NES (Noise Enhanced Stability) effect to measure market dynamics’ stabilizing effect. The approach we propose in this paper belongs to another branch of using a statistical model on time scales. Along with the empirical analysis, we show a broader view of how different companies/sectors behaved across different periods. In particular, we use a mixture-model based statistical methodology to segment the time-series and determine change points.
The mixture-model cluster analysis of regression models is not new. These models are also known as
“cluster-wise regression”,
“latent models”, and
“latent structure models of choice”. These models have been well-studied among statisticians, machine learning researchers, and econometricians in the last several decades to construct time-series segmentation models and identify change points. They have many useful theoretical and applied properties. Mixture-model cluster analysis of regression models is a natural extension of the standard multivariate Gaussian mixture-model cluster analysis. These models are beneficial to study heterogeneous data sets that involve not just one response variable but can have several responses or target-dependent variables simultaneously with a given set of independent variables. Recently, they have been proven to be a precious class of models in various disciplines in
behavioral and economic research,
ecology,
financial engineering,
process control,
and monitoring,
market research,
transportation systems. Additionally, we also witness the mixture model’s usage in the
analysis of scanner panel,
survey, and other choice data to study consumer choice behavior and dynamics Dillon et al. [
7].
In reviewing the literature, we note that Quandt and Ramsey [
8] and Kiefer [
9] studied data sets by applying a mixture of two regression models using moment generating function techniques to estimate the unknown model parameters. Later, De Veaux [
10] developed an EM algorithm to fit a mixture of two regression models. DeSarbo and Cron [
11] used similar estimating equations and extended the earlier work done on a mixture of two regression models to a mixture of K-component regression models. For an excellent review article on this problem, we refer the reviewers to Wedel and DeSarbo [
12].
In terms of these models’ applications in the segmentation of time-series, they can be seen in the early work of Sclove [
13], where the author applied the mixture model to the segmentation of US gross national product, a high dimensional time-series data. Specifically, Sclove [
13] used the statistical model selection criteria to choose the number of classes.
With the currently existing challenges in mind in the segmentation of time-series data, in this paper, our objective and goal are to develop a new methodology which can:
Identify and select variables that are sparse in the MIX-SPCR model.
Treat each time segment continuously in the process with some specified probability density function (pdf).
Determine the number of time-series segments and the number of sparse variables and estimate the structural change points simultaneously.
Develop a robust and efficient algorithm for estimating model parameters.
We aim to achieve these objectives by developing the information complexity () criteria as our fitness function throughout the paper for the segmentation of high-dimensional time-series data.
Our approach involves a two-stage procedure. We first make a variable selection by using SPCA with the benefit of sparsity. We then fit the sparse principal component regression (SPCR) model by transforming the original high dimensional data into several main principal components and estimating relationships between the sparse component loadings and the response variable. In this way, the mixture model not only handles the curse of dimensionality but also maintains the model’s excessive explanatory power. In this manner, we choose the best subset of predictors and determine the number of time-series segments in the MIX-SPCR model simultaneously using .
The rest of the paper is organized as follows. In
Section 2, we present the model and methods. In particular, we first briefly explain sparse principal component analysis (SPCA) due to Zou et al. [
14] in
Section 2.1. In
Section 2.2, we modify SPCA and develop mixtures of the sparse principal component regression (
MIX-SPCR) model for the segmentation of time-series data. In
Section 3, we present a regularized entropy-based Expectation and Maximization (EM) clustering algorithm. As is well known, the EM algorithm performs through maximizing the likelihood of the mixture models. However, to make the conventional EM algorithm robust (not sensitive to initial values) and converge to global optimum, we use the robust version of the EM algorithm for the
MIX-SPCR model based on the work of Yang et al. [
15]. These authors addressed the robustness issue by adding an entropy term of mixture proportions to the conventional EM algorithm’s objective function. While our EM algorithm is in the same spirit of the Yang et al. [
15] approach, there are significant differences between our approach and theirs. Yang’s robust EM algorithm merely deals with the usual clustering problem without involving any response (or dependent) variable or time factor in the data. We extend it to the case of the
MIX-SPCR model in the context of time-series data. In
Section 4, we discuss various information criteria, specifically the information complexity based criteria (
). We derive the
for the
MIX-SPCR model based on Bozdogan’s previous research ([
16,
17,
18,
19,
20]). In
Section 5, we present our Monte Carlo simulation study.
Section 5.2 involves an experiment on the detection of structural points, and
Section 5.3 presents a large scale Monte Carlo simulation verifying the advantage of the
MIX-SPCR with statistical information criteria. We provide a real data analysis in
Section 6 using the daily adjusted closing S&P 500 index and stock prices from the Yahoo Finance database that spans the period from January 1999 to December 2019. Finally, our conclusion and discussion are presented in
Section 7.
2. Model and Methods
In this section, we briefly present the sparse principal component analysis (SPCA), sparse principal component regression (SPCR) as a background. Then, by hybridizing these two methods within the mixture model, we propose the mixture-model cluster analysis of sparse principal component regression (abbreviated as MIX-SPCR model hereafter), for segmentation of high dimensional time-series datasets. Compared with a simple linear combination of all explanatory variables (i.e., the dense PCA model), the new approach interprets better because it maintains a sparsity specification.
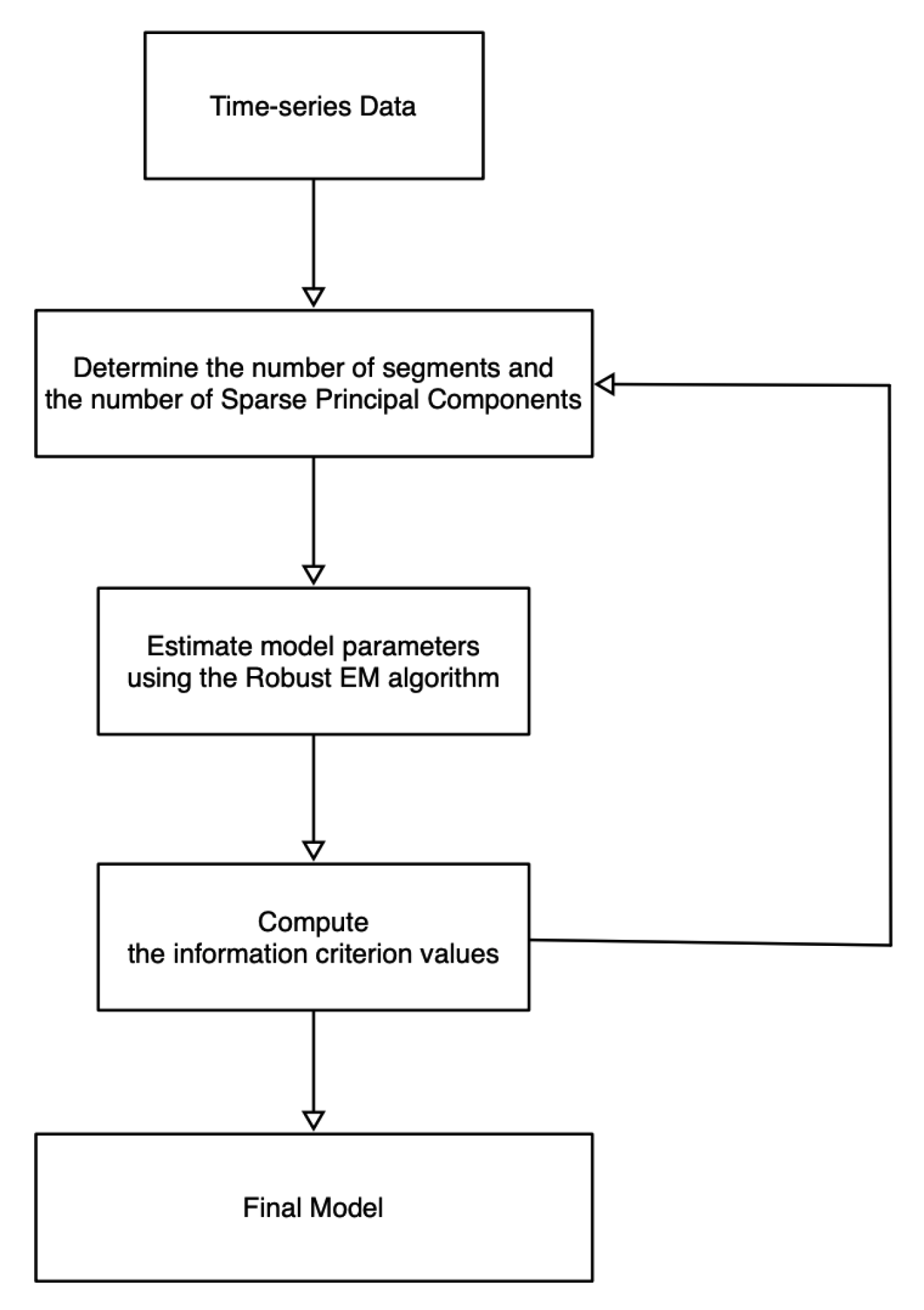
Referring to
Figure 1, we first show the overall structure of the model in this paper. The overall processing flow is that we clean and standardize the data after obtaining the time-series data. Subsequently, we specify the number of time-series segments and how many Sparse Principal Components (SPCs) each segment contains. Using the Robust EM algorithm (
Section 3), we estimate the model parameters, especially the boundaries (also known as
change points) of each time segment. The information criterion values are calculated using the method of
Section 4. By testing different numbers of time segments/SPCs, we obtain multiple criterion values. According to the calculated information criterion values, we choose the most appropriate model with the estimated parameters.
2.1. Sparse Principal Component Analysis (SPCA)
Given the input data matrix,
with
n number of observations and
p variables, we decompose
using the singular value decomposition (SVD). We write the decomposition procedure as
, where
is a diagonal matrix of singular values and orthogonal columns
and
as the left and right singular vectors. When we perform SVD of a data matrix
that has been centered, by subtracting each column’s mean, the process is the well-known
principal component analysis (
PCA). As discussed by Zou et al. [
14], PCA has several advantages as compared with other dimensionality reduction techniques. For example, the PCA can sequentially identify the source of variability by considering the linear combination of all the variables. Because of the orthonormal constraint during the computation, all the calculated
principal components (
PCs) have clear geometrical interpretation corresponding to the original data space as a dimension reduction technique. Because PCA can deal with
“the curse of dimensionality” of high-dimensional data sets, it has been widely used in real-world scenarios, including biomedical and financial applications.
Even though PCA has excellent properties that are desirable in real-world applications and statistical analysis, the interpretation of PCs is often difficult since it includes all the variables as linear combinations of all the original variables in each of the PCs. In practice, the principal components always have a large number of non-zero coefficient values for corresponding variables. To resolve this drawback, researchers proposed various improvements focusing on PCA’s sparsity while maintaining the minimal loss of information. Shen and Huang [
21] designed an algorithm to iteratively extract top PCs using the so-called
penalized least sum of square (
PLSS) criterion. Zou et al. [
14] utilized the lasso penalty (via Elastic Net) to maintain a sparse loading of the principal components, which is named
sparse principal component analysis (
SPCA).
In this paper, we use the sparse principal component analysis (SPCA) proposed by Zou et al. [
14]. Given the data matrix
, we minimize the objective function to obtain the SPCA results:
subject to
where
is the identity matrix. We maintain the hyperparameters
and
to be non-negative. The
and
matrices of size
are given by
and
If we choose the first k principal components from the data matrix , then the estimate contains the sparse loading vectors, which are no longer orthogonal.
A bigger means a greater penalty for having non-zero entries in . By using different , we control the number of zeros in the jth loading vector. If for , this problem reduces to usual PCA.
Zou et al. [
14] proposed a generalized SPCA algorithm to solve the optimization problem in Equation (
1). The algorithm applies the Elastic Net (EN) to estimate
iteratively and update matrix
. However, this algorithm is not the only available approach for extracting principal components with sparse loadings. The SPCA could also be computed through dictionary learning by Mairal et al. [
22]. By introducing the probability model of principal component analysis, SPCA is equivalent to the
sparse probabilistic principal component analysis (
SPPCA) if the prior is Laplacian distribution for each weight matrix element (Guan and Dy [
23], Williams [
24]). For further discussion on SPPCA, we refer readers to those related publications for more details.
Next, we introduce the MIX-SPCR model for the segmentation of time-series data.
2.2. Mixtures of SPCR Model for Time-Series Data
Suppose the continuous response variable is denoted as , where n represents the number of observations (time points). Similarly, we have the predictors denoted as . Each observation has p dimensions and is represented as . Both the response variable and independent variables are collected sequentially labeled by time points .
The finite mixture model allows applying cluster analysis on conditionally dependent data into several classes. In the time-series data scenario, researchers cluster the data into several homogeneous groups where the number of groups G is unknown in general. Within each group, we apply the SPCA to extract top k principal components that each of them has a sparse loading of p variable coefficients. The extracted top k PCs are denoted as matrix . We also use to represent the principal component matrix obtained from the group indexed by .
The SPCR model assumes that each pair
is independently drawn from a cluster using both the SPCA and the regression model as follows.
where
.
For each group
g, the random error is assumed to be Gaussian distributed. That is,
. If the response variable is multivariate, then the random error is usually also assumed to be a multivariate Gaussian distribution. Thus the probability density function (pdf) of the SPCR model is
We emphasize here that the noise (i.e., the error term) included in the statistical model is drawn from a normal distribution independent for each time-series segment, with different values of
for each period. Since we use the EM algorithm to estimate the parameters of the model, the noise parameter
can be estimated accurately as well. Future studies will consider introducing different noise distributions, such as
-stable Lévy noise [
25], and other non-Gaussian noise distributions to further extend the current model.
We also consider time factor
in the SPCR model of time-series data to be continuous. The pdf of the time factor is
where
is the mean, and
is the variance of the time segment
g. Apart from the normal distribution, our approach can also be generalized to other distributions for the time factor, such as skewed distributions, Student’s t-distribution, ARCH, GARCH time-series models, and so on.
As a result, if we use the
MIX-SPCR model to perform segmentation of time-series data, the likelihood function of the whole data
with
G number of clusters (or segments) is given by
where the
is the mixing proportion with the constraint that
and
. We follow the definition of missing values by Yang et al. [
15] and let
. If
, then
, otherwise,
. Then the log-likelihood function of the
MIX-SPCR model models is
We denote where and .
Given the number of segments, researchers usually apply the EM algorithm to determine the optimal segmentation by setting the objective function as
(Gaffney and Smyth [
26], Esling and Agon [
27], Gaffney [
28]).
4. Information Complexity Criteria
Recently, the statistical literature recognized the necessity of introducing model selection as one of the technical areas. In this area, the entropy and the Kullback–Leibler [
29] information (or KL distance) play a crucial role and serve as an analytical basis to obtain the forms of model selection criteria. In this paper, we use information criteria to evaluate a portfolio of competing models and select the best-fitting model with minimum criterion values.
One of the first information criteria for model selection in the literature is due to the seminal work of Akaike [
30]. Following the entropy maximization principle (EMP), Akaike developed the Akaike’s Information Criterion (
) to estimate the expected KL distance or divergence. The form of
is
where
is the maximized likelihood function, and
k is the number of estimated free parameters in the model. The model with minimum
value is chosen as the best model to fit the data.
Motivated by Akaike’s work, Bozdogan [
16,
17,
18,
19,
20,
31] developed a new information complexity (
) criteria based on Van Emden’s [
32] entropic complexity index in parametric estimation. Instead of penalizing the number of free parameters directly,
penalizes the covariance complexity of the model. There are several forms of
. In this section, we present the two general forms of
criteria based on the estimated inverse Fisher information matrix (IFIM). The first form is
where
is the maximized likelihood function, and
represents the entropic complexity of IFIM. We define
as
and where
. We can also give the form of
in terms of eigenvalues,
where
is the arithmetic mean of the eigenvalues,
, and
is the geometric mean of the eigenvalues.
We note that penalizes the lack of parsimony and the profusion of the model’s complexity through IFIM. It offers a new perspective beyond counting and penalizing number of estimated parameters in the model. Instead, takes into account interaction (i.e., correlation) among the estimated parameters through the model fitting process.
We define the second form of
as
where
is given by
In terms of the eigenvalues of IFIM, we write
as
We want to highlight some features of here. The term is a second-order equivalent measure of complexity to the original term . Additionally, we note that is scale-invariant and with only when all . Furthermore, measures the relative variation in the eigenvalues.
These two forms of provide us an easy to use computational means in high dimensional modeling. Next, we derive the analytical forms of in the MIX-SPCR model.
5. Monte Carlo Simulation Study
We perform numerical experiments in a unified computing environment: Ubuntu 18.04 operating system, Intel I7-8700, and 32 GB of RAM. We use the programming language Python and the scientific computing package NumPy [
34] to build a computational platform. The size of the input data directly affects the running time of the program. At
time-series observations, the execution time for each EM iteration is about 0.9 s. Parameter estimation can reach convergence within 40 steps of iterations, with a total machine run time of 37 s.
5.1. Simulation Protocol
In this section, we present the performance of the proposed
MIX-SPCR model using synthetic data generated from a segmented regression model. Our simulation protocol has
variables and four actual latent variables. Two segmented regression models determine the dependent variable
y, and each segment is continuous and has its own specified coefficients (
and
). Our simulation set up is as follows:
We set the total number of time-series observations, . The first segment has , and the second segment has time-series observations. We randomly draw error term from a Gaussian distribution with zero mean and . Among all the variables, the first six observable variables explain the first segment, and the remaining six explanatory variables primarily determine the second segment. We set the mixing proportions and for two time-series segments, respectively.
5.2. Detection of Structural Change Point
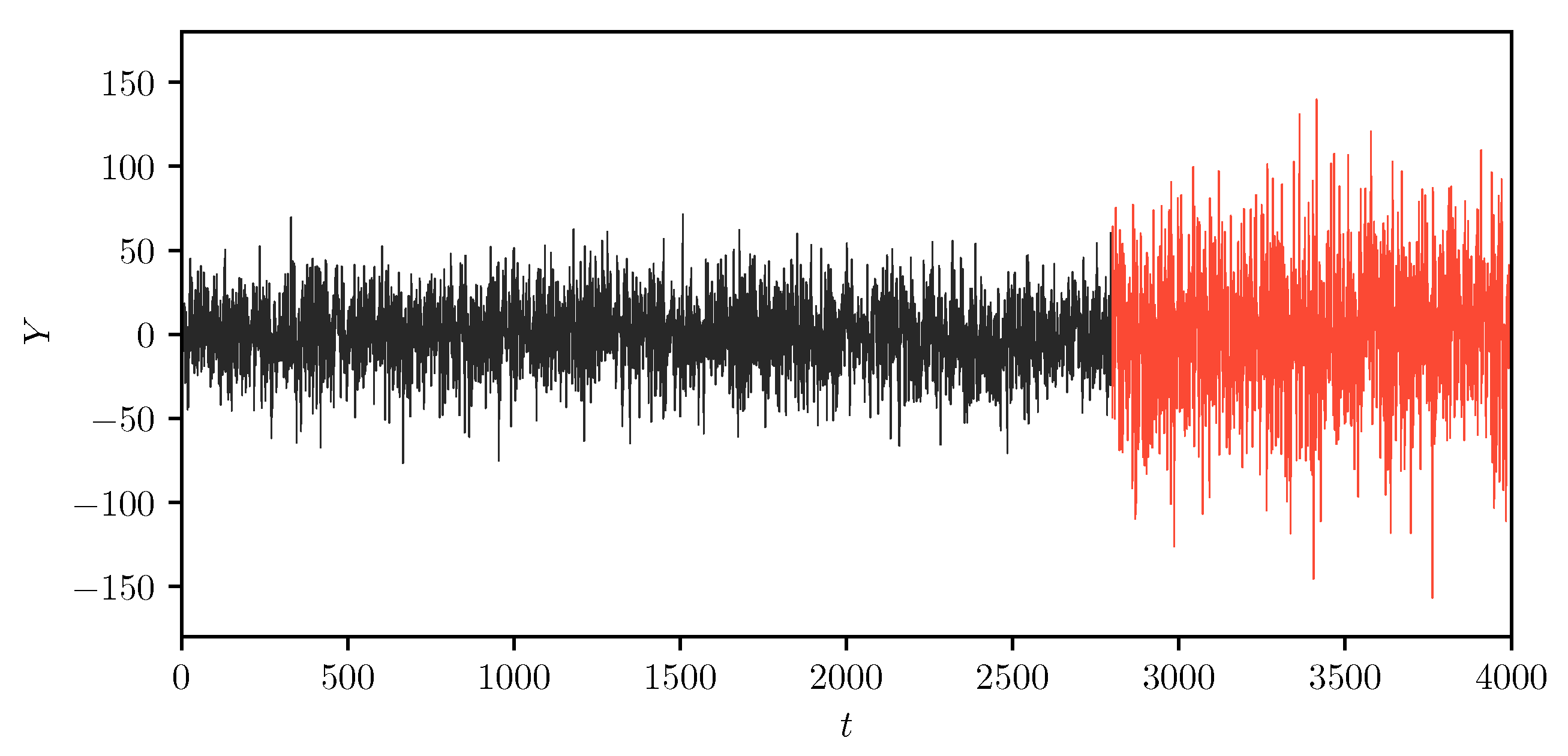
In the first simulation study, we limit the actual number of segments equal to two, which means that the first segment expands from the starting point to a structural change point, and the second segment expands from the change point to the end. By design, each segment is continuous on the time scale, and different sets of independent variables explain the trending and volatility. We run the MIX-SPCR model to see if it can successfully determine the position of the change point using the information criteria. If a change point is correctly selected, we expect that the information criteria is minimized at this change point.
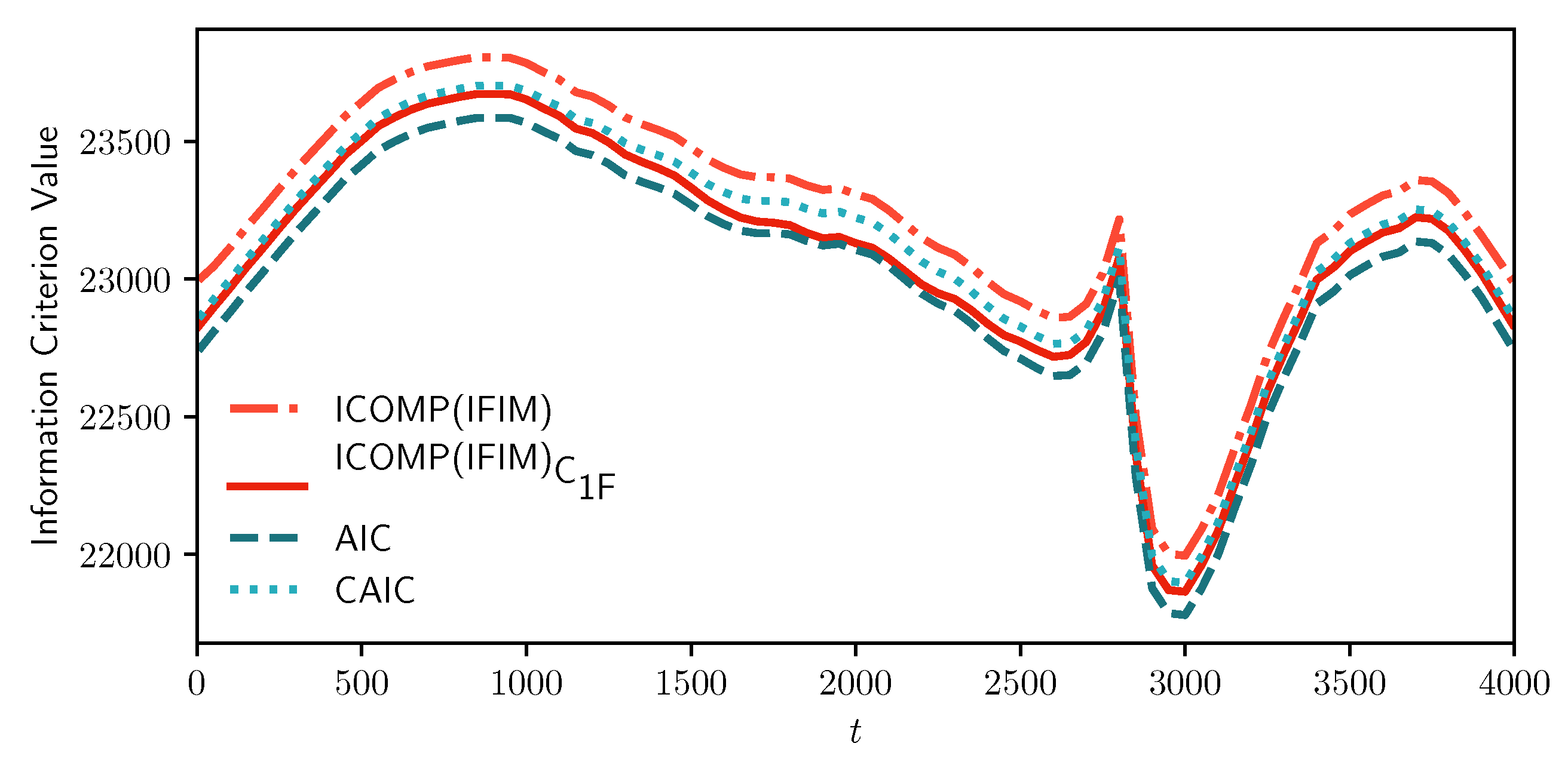
Figure 2 and
Figure 3 show our results from the
MIX-SPCR model. Specifically, it shows the sample path of the information criteria at each time point. We note that all the information criteria values are minimized from
to
, which covers the time-series’s actual change point position. As the
MIX-SPCR model selects different change points, the penalty term of
and
remain the same because both the number of model parameters and the number of observations do not change. In this simulation scenario, the fixed penalty term means that the
and
reflect the changes only in the “lack of fit” term of various models without considering model complexity. This indicates that using AIC-type criteria just counting and penalizing the number of parameters may be necessary but not sufficient in model selection. As a comparison, however, we note that the penalty term of information complexity-based criteria,
and
, are adjusted in selecting different change points. They are varying but not fixed.
5.3. A Large-Scale Monte Carlo Simulation
Next, we perform a large-scale Monte Carlo simulation to illustrate the
MIX-SPCR model’s performance in choosing the correct number of segments and the number of latent variables. A priori, in this simulation, we pretend that we do not know the actual structure of the data and use the information criteria to recover the actual construction of the
MIX-SPCR model. To achieve this, we follow the above simulation protocol using a different number of time points by varying
, 2000, 4000. As before, there are twelve explanatory variables drawn from four latent variable models generated from a multivariate Gaussian distribution given in Equation (47). The simulated data again consist of two time-series segments with mixing proportions
and
, respectively. For each data generating process, we replicate the simulation one hundred times and record both information complexity-based criteria (
&
) and classic AIC-type criteria (
&
). In
Table 1, we present how many times the
MIX-SPCR model selects different models in the one hundred simulations. In this way, we can assess different information criteria by measuring the hit rates.
Looking at
Table 1, we see that when the sample size
(small),
selects the correct model (
,
) 69 times,
selects 80 times,
selects 48 times, and
selects 76 times, respectively, in 100 replications of the Monte Carlo simulation. When the sample size is small,
tends to choose a sparser regression model sensitive to the sample size. However, as the sample size increases, when
and
,
consistently outperforms other information criteria in terms of hit rates. The percentage of the correctly identified model is above 90%, as reported above.
Our results show that the MIX-SPCR model works well in all settings to estimate the number of time-series segments and the number of latent variables.
Figure 4 illustrates how the
MIX-SPCR model performs if the number of segments and the number of sparse principal components are unknown beforehand.
The choice of the number of segments (G) has a significant impact on the results. For all the simulation scenarios, the correct choice of the number of segments () has information criterion values less than the incorrect choice (). This pattern emerges consistently among all the sample sizes, both the classical ones and information-complexity based criteria.
In summary, the large-scale Monte Carlo simulation analysis highlights the performance of the
MIX-SPCR model. As the sample size increases, the
MIX-SPCR model improves its performance. As shown in
Figure 3, the
MIX-SPCR model can efficiently determine the structural change point and estimate the mixture proportions when the number of segments is unknown beforehand. Another key finding is that, by using the appropriate information criteria, the
MIX-SPCR model can correctly identify the number of segments and the number of latent variables from the data. In other words, our approach can extract the main factors not only from the intercorrelated variables but also classify the data into several clearly defined segments on the time scale.
7. Conclusions and Discussions
In this paper, we presented a new and novel method to segment high-dimensional time-series data into different clusters or segments using the mixture model of the sparse principal components model (MIX-SPCR). The MIX-SPCR model considers both the relationships among the predictor variables and how various predictor variables contribute the explanatory power to the response variable through the sparsity settings. Information criteria have been introduced and derived for the MIX-SPCR model. These criteria are applied to study their performance under different sample sizes and to select the best-fitting model.
Our large-scale Monte Carlo simulation exercise showed that the MIX-SPCR model could successfully identify the real structure of the time-series data using the information criteria as the fitness function. In particular, based on our results, the information complexity-based criteria—i.e., and —outperformed the conventional standard information criteria, such as the AIC-type criteria as the data dimension and the sample size increase.
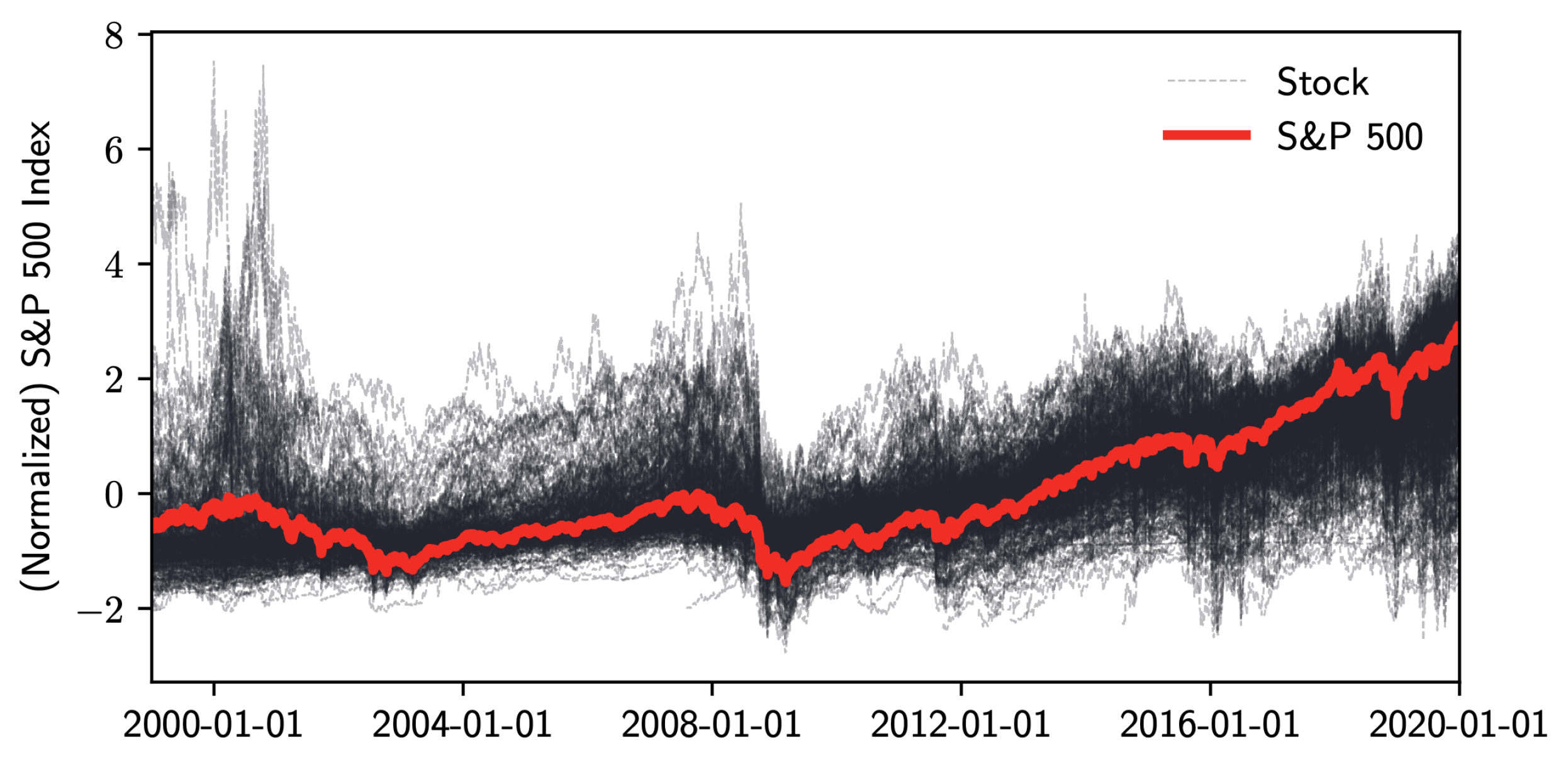
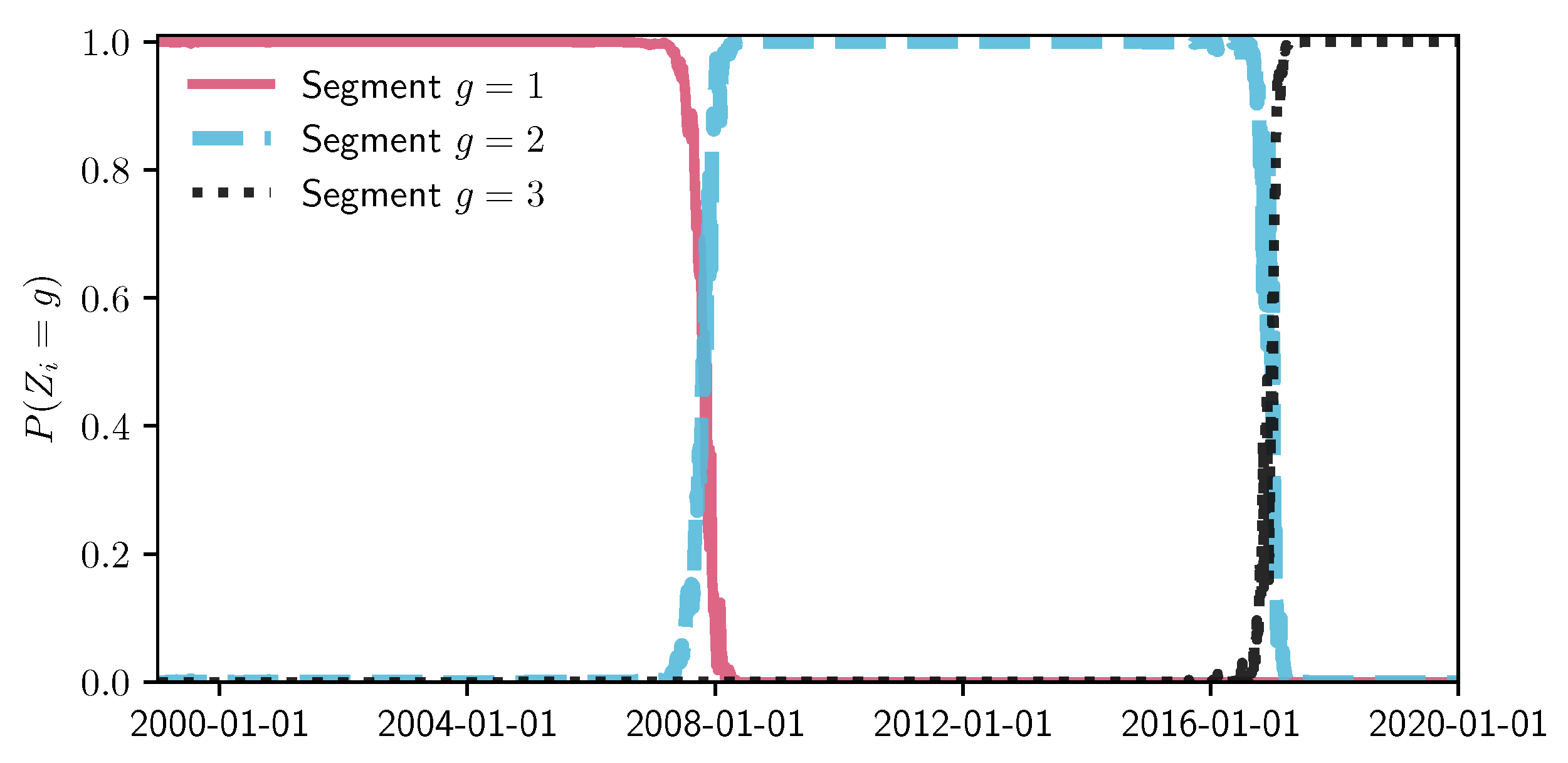
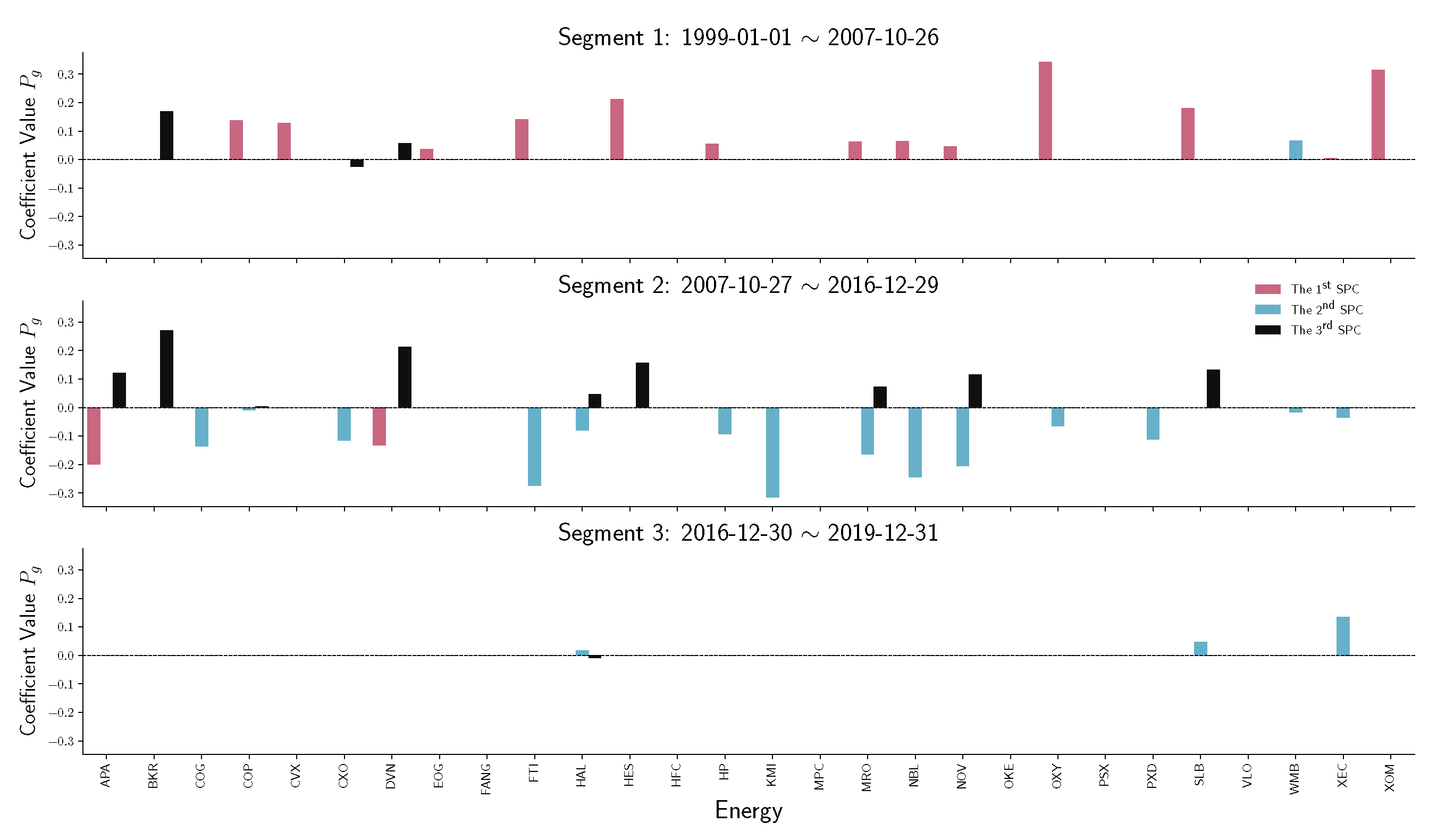
Later, we empirically applied the MIX-SPCR model to uncover the S&P 500 index data (from 1999 to 2019) and identify two change points of this data set.
We observe that the first change point physically coincides with the early stages of the 2008 financial crisis. The second change point is immediately after the 2016 United States presidential election. This structural change point coincides with the election of President Trump and his transition.
Our findings showed how the S&P 500 index and company stock prices react within each time-series segment. The MIX-SPCR model presents excessive explanatory power by identifying how different sectors fluctuated before/after the Federal Reserve’s addressing heightened liquidity from 10 March to 14 March 2008.
Although this is not a traditional event study paper, it is the first paper to use the sparse principal component regression model with mixture models in the time-series analysis. The proposed new and novel MIX-SPCR model enlightens us to explore more interpretable results on how macroeconomic factors/events influence the stock prices on the time scale. Later, in a separate paper, we will incorporate the event study in the MIX-SPCR model as our future research initiative.
This paper’s time segmentation model builds on time-series data, constructs likelihood functions, and performs parameter estimation by introducing error information unique to each period. Researchers have recently realized that environmental background noise can positively affect the model building and analysis under certain circumstances ([
36,
37,
38,
39,
40,
41,
42]). For example, in Azpeitia and Wagner [
40], the authors highlighted that the introduction of noise is necessary to obtain information about the system. In our next study, we would like to explore this positive effect of environmental noise even further and use it to build better statistical models for analyzing high-dimensional time-series data.