Adaptive Neuro-Fuzzy Inference System and a Multilayer Perceptron Model Trained with Grey Wolf Optimizer for Predicting Solar Diffuse Fraction
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Normalization
2.3. Methods
2.3.1. Multi-Layered Perceptron (MLP)
- Global irradiance;
- Beam normal irradiance;
- Sunshine index;
- kt (clearance index–global/extraterrestrial);
- k (diffuse/extraterrestrial).
2.3.2. MLP-GWO
- The fitness of all solutions are calculated and the top three solutions are selected as alpha, beta and delta wolves until the algorithm is finished.
- In each iteration, the top three solutions (alpha, beta and delta wolves) are able to estimate the hunting position and do so, in each iteration.
- In each iteration, after determining the position of alpha, beta and delta wolves, the position of the rest of the solutions are updated by following them. During each iteration, the vectors, a and c, are updated.
- At the end of the iterations, the position of the alpha wolf is presented as the “optimal point”.
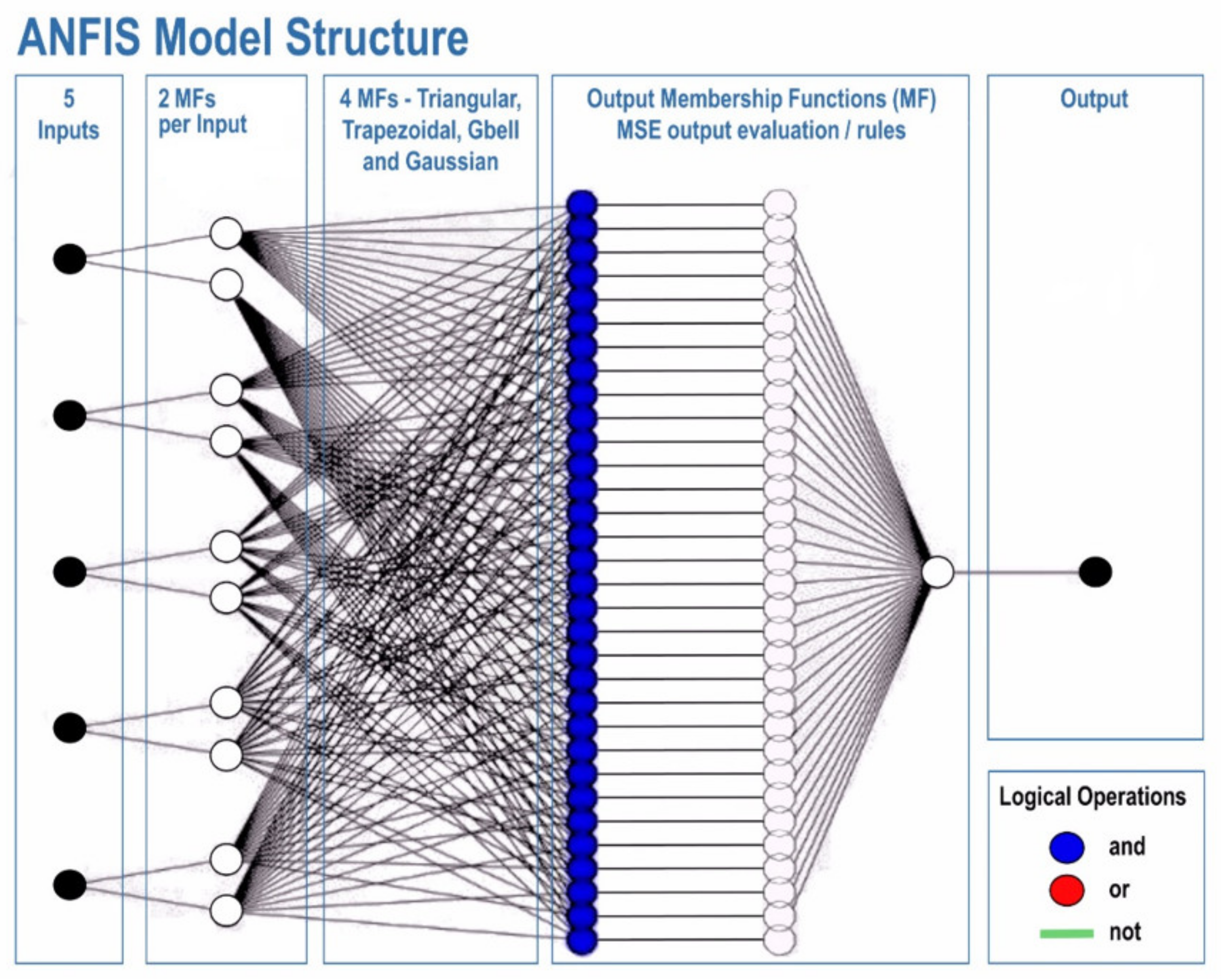
2.3.3. ANFIS
2.4. Evaluation Criteria
3. Results
3.1. Training Results
3.2. Testing Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclatures
| DF | Diffuse Fraction |
| MLP | Multi-Layered Perceptron |
| ML | Machine Learning |
| ANFIS | Adaptive Network-based Fuzzy Inference System |
| GWO | Grey Wolf Optimizer |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| LUE | Light Use Efficiency |
| IEA | International Energy Agency |
| PV | Photo Voltaic |
| ANN | Artificial Neural Network |
| MSE | Mean Square Error |
| MF | Membership Function |
| ANOVA | Analysis of Variance |
| NREL | National Renewable Energy Laboratory |
References
- Li, D.H.; Cheung, K.L.; Lam, T.N.; Chan, W.W.J.A.E. A study of grid-connected photovoltaic (PV) system in Hong Kong. Appl. Energy 2012, 90, 122–127. [Google Scholar] [CrossRef]
- Li, D.H.; Yang, L.; Lam, J.C.J.E. Zero energy buildings and sustainable development implications—A review. Energy 2013, 54, 1–10. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R.J.S.e. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Li, D.H.; Lou, S.; Lam, J.C.; Wu, R.H.J.E. Determining solar irradiance on inclined planes from classified CIE (International Commission on Illumination) standard skies. Energy 2016, 101, 462–470. [Google Scholar] [CrossRef]
- Lou, S.; Li, D.H.; Lam, J.C.; Lee, E.W.J.B. Environment. Estimation of obstructed vertical solar irradiation under the 15 CIE Standard Skies. Build. Environ. 2016, 103, 123–133. [Google Scholar] [CrossRef]
- Kontoleon, K.J.A.E. Glazing solar heat gain analysis and optimization at varying orientations and placements in aspect of distributed radiation at the interior surfaces. Appl. Energy 2015, 144, 152–164. [Google Scholar] [CrossRef]
- Kong, C.; Xu, Z.; Yao, Q.J.A.E. Outdoor performance of a low-concentrated photovoltaic–thermal hybrid system with crystalline silicon solar cells. Appl. Energy 2013, 112, 618–625. [Google Scholar] [CrossRef]
- Kirn, B.; Brecl, K.; Topic, M.J.S.E. A new PV module performance model based on separation of diffuse and direct light. Sol. Energy 2015, 113, 212–220. [Google Scholar] [CrossRef]
- Carrer, D.; Ceamanos, X.; Moparthy, S.; Vincent, C.; C Freitas, S.; Trigo, I.F.J.R.S. Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under All Sky Conditions in the Framework of the LSA SAF Program (Part 1: Methodology). Remote. Sens. 2019, 11, 2532. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; da Rocha, H.R.; Rap, A.; Bonal, D.; Butt, N.; Coupe, N.R.; Shugart, H.H. Simulation of the unexpected photosynthetic seasonality in Amazonian evergreen forests by using an improved diffuse fraction-based light use efficiency model. J. Geophys. Res. Biogeosciences 2017, 122, 3014–3030. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; Yu, K.L.; Wang, B.; Yu, Q.; Bohrer, G.; Billesbach, D.; Bracho, R.; Rahman, F.; Shugart, H.H. A Novel Diffuse Fraction-Based Two-Leaf Light Use Efficiency Model: An Application Quantifying Photosynthetic Seasonality across 20 AmeriFlux Flux Tower Sites. J. Adv. Model. Earth Syst. 2017, 9, 2317–2332. [Google Scholar] [CrossRef]
- Li, D.H.; Tang, H.L.; Lee, E.W.; Muneer, T. Classification of CIE standard skies using probabilistic neural networks. Int. J. Clim. 2010, 30, 305–315. [Google Scholar] [CrossRef]
- Shamshirband, S.; Rabczuk, T.; Chau, K.W. A survey of deep learning techniques: Application in wind and solar energy resources. IEEE Access. 2019, 7, 164650–164666. [Google Scholar] [CrossRef]
- Nosratabadi, S.; Mosavi, A.; Duan, P.; Ghamisi, P.; Filip, F.; Band, S.S.; Reuter, U.; Gama, J.; Gandomi, A.H. Data Science in Economics: Comprehensive Review of Advanced Machine Learning and Deep Learning Methods. Mathematics 2020, 8, 1799. [Google Scholar] [CrossRef]
- Abal, G.; Aicardi, D.; Suárez, R.A.; Laguarda, A.J.S.E. Performance of empirical models for diffuse fraction in Uruguay. Sol. Energy 2017, 141, 166–181. [Google Scholar] [CrossRef]
- Paulescu, E.; Blaga, R.J.S.E. A simple and reliable empirical model with two predictors for estimating 1-minute diffuse fraction. Sol. Energy 2019, 180, 75–84. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Chen, Y.; Wang, D.J.E.P. General models for estimating daily diffuse solar radiation in China: Diffuse fraction and diffuse coefficient models. Energy Procedia 2019, 158, 351–356. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Baghban, A.; Sadeghzadeh, M.; Zamen, M.; Mosavi, A.; Shamshirband, S.; Kumar, R.; Mohammadi-Khanaposhtani, M. Evaluation of electrical efficiency of photovoltaic thermal solar collector. Eng. Appl. Comput. Fluid Mech. 2020, 14, 545–565. [Google Scholar] [CrossRef]
- Wilcox, S.; Myers, D.R. Evaluation of Radiometers in Full-Time Use at the National Renewable Energy Laboratory Solar Radiation Research Laboratory; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2008. [Google Scholar]
- Claywell, R.; Muneer, T.; Asif, M.J.J.S.E.E. An efficient method for assessing the quality of large solar irradiance datasets. J. Sol. Energy Eng. 2005, 127, 150–152. [Google Scholar] [CrossRef]
- Scarpa, F.; Marchitto, A.; Tagliafico, L.J.I.J.H.T. Splitting the solar radiation in direct and diffuse components; Insights and constrains on the clearness-diffuse fraction representation. Int. J. Heat Technol. 2017, 35, 325–329. [Google Scholar] [CrossRef][Green Version]
- Mishra, S.; Palanisamy, P. Multi-time-horizon solar forecasting using recurrent neural network. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 18–24. [Google Scholar]
- Qing, X.; Niu, Y.J.E. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Jamil, B.; Akhtar, N.J.E. Estimation of diffuse solar radiation in humid-subtropical climatic region of India: Comparison of diffuse fraction and diffusion coefficient models. Energy 2017, 131, 149–164. [Google Scholar] [CrossRef]
- Tapakis, R.; Michaelides, S.; Charalambides, A.G.J.S.E. Computations of diffuse fraction of global irradiance: Part 2—Neural networks. Sol. Energy 2016, 139, 723–732. [Google Scholar] [CrossRef]
- Lauret, P.; Boland, J.; Ridley, B. Derivation of a solar diffuse fraction model in a Bayesian framework. Case Stud. Business Ind. Gov. Stat. 2014, 3, 108–122. [Google Scholar]
- Elminir, H.K.; Azzam, Y.A.; Younes, F.I.J.E. Prediction of hourly and daily diffuse fraction using neural network, as compared to linear regression models. Energy 2007, 32, 1513–1523. [Google Scholar] [CrossRef]
- Francisco, F.J.B. Radiación solar y aspectos climatológicos de Almería: 1990–1996; Universidad Almería: Almería, Spain, 1998; Volume 6. [Google Scholar]
- Kundu, P.; Paul, V.; Kumar, V.; Mishra, I.M.J.C.E.R. Design. Formulation development, modeling and optimization of emulsification process using evolving RSM coupled hybrid ANN-GA framework. Chem. Eng. Res. Des. 2015, 104, 773–790. [Google Scholar] [CrossRef]
- Ardabili, S.F.; Mahmoudi, A.; Gundoshmian, T.M. Modeling and simulation controlling system of HVAC using fuzzy and predictive (radial basis function, RBF) controllers. J. Build. Eng. 2016, 6, 301–308. [Google Scholar] [CrossRef]
- Pal, S.K.; Mitra, S. Multilayer perceptron, fuzzy sets, classifiaction. Neural Comput. Appl. 1992. [Google Scholar] [CrossRef]
- Amid, S.; Mesri Gundoshmian, T. Prediction of output energies for broiler production using linear regression, ANN (MLP, RBF), and ANFIS models. Environ. Prog. Sustain. Energy 2017, 36, 577–585. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.-w. Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 2019, 12, 289. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Varkonyi-Koczy, A. Building Energy information: Demand and consumption prediction with Machine Learning models for sustainable and smart cities. Smart Ind. Smart Educ. 2019. [Google Scholar] [CrossRef]
- Gundoshmian, T.M.; Ardabili, S.; Mosavi, A.; Varkonyi-Koczy, A.R. Prediction of combine harvester performance using hybrid machine learning modeling and response surface methodology. Smart Ind. Smart Educ. 2019. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Várkonyi-Kóczy, A.R. Advances in machine learning modeling reviewing hybrid and ensemble methods. In Proceedings of the International Conference on Global Research and Education, Budapest, Hungary, 4–7 September 2019; pp. 215–227. [Google Scholar]
- Nazari, M.; Shamshirband, S. The particle filter-based back propagation neural network for evapotranspiration estimation. Ish J. Hydraul. Eng. 2020, 26, 191–201. [Google Scholar] [CrossRef]
- Huang, K.-T.J.R.E. Identifying a suitable hourly solar diffuse fraction model to generate the typical meteorological year for building energy simulation application. Renew. Energy 2020. [Google Scholar] [CrossRef]
- Chang, K.-C.; Lin, C.-T.; Chen, C.-C.J.O.; Electronics, Q. Monitoring investigation of solar diffuse fraction in Taiwan. Opt. Quantum Electron. 2018, 50, 439. [Google Scholar] [CrossRef]
- Li, F.; Hu, C.; Ma, N.; Yan, Q.; Chen, Z.; Shen, Y.J.T.X.A.E.S.S. Modeling of Diffuse Fraction in Beijing Based on K-Means and SVM in Multi-Time Scale. Taiyangneng Xuebao/Acta Energ. Sol. Sin. 2018, 39, 2515–2522. [Google Scholar]
- Hofmann, M.; Seckmeyer, G.J.E. Influence of various irradiance models and their combination on simulation results of photovoltaic systems. Energies 2017, 10, 1495. [Google Scholar] [CrossRef]
- Rojas, R.G.; Alvarado, N.; Boland, J.; Escobar, R.; Castillejo-Cuberos, A.J.R.E. Diffuse fraction estimation using the BRL model and relationship of predictors under Chilean, Costa Rican and Australian climatic conditions. Renew. Energy 2019, 136, 1091–1106. [Google Scholar] [CrossRef]
- Dervishi, S.; Mahdavi, A.J.S.E. Computing diffuse fraction of global horizontal solar radiation: A model comparison. Sol. Energy 2012, 86, 1796–1802. [Google Scholar] [CrossRef]
- Mosavi, A.; Faghan, Y.; Ghamisi, P.; Duan, P.; Ardabili, S.F.; Salwana, E.; Band, S.S. Comprehensive Review of Deep Reinforcement Learning Methods and Applications in Economics. Mathematics 2020, 8, 1640. [Google Scholar] [CrossRef]
- Shamshirband, S.; Fathi, M.; Chronopoulos, A.T.; Montieri, A.; Palumbo, F.; Pescapè, A. Computational intelligence intrusion detection techniques in mobile cloud computing environments: Review, taxonomy, and open research issues. J. Inf. Secur. Appl. 2020, 55, 102582. [Google Scholar] [CrossRef]



| Input Data | Output |
|---|---|
| Global Irradiance (W/m2) Beam Irradiance (W/m2) Sunshine Duration Index kt (Global/Extraterrestrial-Clearance Index) k (Diffuse/Extraterrestrial) | kd (Global/Diffuse-Diffuse Fraction) |
| Parameters | Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|---|
| Global Irradiance*kd | (Combined) | 362.670 | 6261 | 0.058 | 2.423 | 0.000 |
| Linearity | 158.377 | 1 | 158.377 | 6624.567 | 0.000 | |
| Deviation from Linearity | 204.292 | 6260 | 0.033 | 1.365 | 0.000 | |
| Beam Irradiance*kd | (Combined) | 342.804 | 6073 | 0.056 | 2.083 | 0.000 |
| Linearity | 190.532 | 1 | 190.532 | 7031.608 | 0.000 | |
| Deviation from Linearity | 152.272 | 6072 | 0.025 | 0.925 | 0.998 | |
| Sunshine Duration Index*kd | (Combined) | 174.180 | 20 | 8.709 | 316.456 | 0.000 |
| Linearity | 154.287 | 1 | 154.287 | 5606.259 | 0.000 | |
| Deviation from Linearity | 19.893 | 19 | 1.047 | 38.045 | 0.000 | |
| kt*kd | (Combined) | 374.097 | 776 | 0.482 | 49.110 | 0.000 |
| Linearity | 194.204 | 1 | 194.204 | 19,783.581 | 0.000 | |
| Deviation from Linearity | 179.894 | 775 | 0.232 | 23.646 | 0.000 | |
| k*kd | (Combined) | 374.097 | 776 | 0.482 | 49.110 | 0.000 |
| Linearity | 194.204 | 1 | 194.204 | 19,783.581 | 0.000 | |
| Deviation from Linearity | 179.894 | 775 | 0.232 | 23.646 | 0.000 | |
| No. of Neurons in the Hidden Layer | MAE | RMSE | ME |
|---|---|---|---|
| 15 | 0.329652 | 0.381277 | 0.0860 |
| 20 | 0.283239 | 0.167089 | 0.0751 |
| 25 | 0.303247 | 0.160102 | 0.0934 |
| 30 | 0.294706 | 0.187014 | 0.0886 |
| Description | MF Type | MAE | RMSE | ME |
|---|---|---|---|---|
| No. of MFs = 2 Optimum method = hybrid Output MF type = linear | Triangular | 0.252980 | 0.341010 | 0.0749 |
| Trapezoidal | 0.267428 | 0.096249 | 0.0768 | |
| Gbell | 0.253935 | 0.089634 | 0.0748 | |
| Gaussian | 0.251187 | 0.025520 | 0.0745 |
| No. of Population | MAE | RMSE | ME |
|---|---|---|---|
| 100 | 0.262107 | 0.343945 | 0.0733 |
| 200 | 0.253794 | 0.093941 | 0.0786 |
| 300 | 0.247638 | 0.088364 | 0.0718 |
| 400 | 0.25512 | 0.097463 | 0.0736 |
| Model Name | MAE | RMSE | ME |
|---|---|---|---|
| MLP | 0.503710 | 0.550427 | 0.4589 |
| ANFIS | 0.422157 | 0.516688 | 0.4392 |
| MLP-GWO | 0.077281 | 0.114355 | 0.3328 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Claywell, R.; Nadai, L.; Felde, I.; Ardabili, S.; Mosavi, A. Adaptive Neuro-Fuzzy Inference System and a Multilayer Perceptron Model Trained with Grey Wolf Optimizer for Predicting Solar Diffuse Fraction. Entropy 2020, 22, 1192. https://doi.org/10.3390/e22111192
Claywell R, Nadai L, Felde I, Ardabili S, Mosavi A. Adaptive Neuro-Fuzzy Inference System and a Multilayer Perceptron Model Trained with Grey Wolf Optimizer for Predicting Solar Diffuse Fraction. Entropy. 2020; 22(11):1192. https://doi.org/10.3390/e22111192
Chicago/Turabian StyleClaywell, Randall, Laszlo Nadai, Imre Felde, Sina Ardabili, and Amirhosein Mosavi. 2020. "Adaptive Neuro-Fuzzy Inference System and a Multilayer Perceptron Model Trained with Grey Wolf Optimizer for Predicting Solar Diffuse Fraction" Entropy 22, no. 11: 1192. https://doi.org/10.3390/e22111192
APA StyleClaywell, R., Nadai, L., Felde, I., Ardabili, S., & Mosavi, A. (2020). Adaptive Neuro-Fuzzy Inference System and a Multilayer Perceptron Model Trained with Grey Wolf Optimizer for Predicting Solar Diffuse Fraction. Entropy, 22(11), 1192. https://doi.org/10.3390/e22111192







