Surface Thermodynamics, Viscosity, Activation Energy of N-Methyldiethanolamine Aqueous Solutions Promoted by Tetramethylammonium Arginate
Abstract
:1. Introduction
2. Experimental
2.1. Reagents
2.2. Instrumentation and Process
3. Results and Discussion
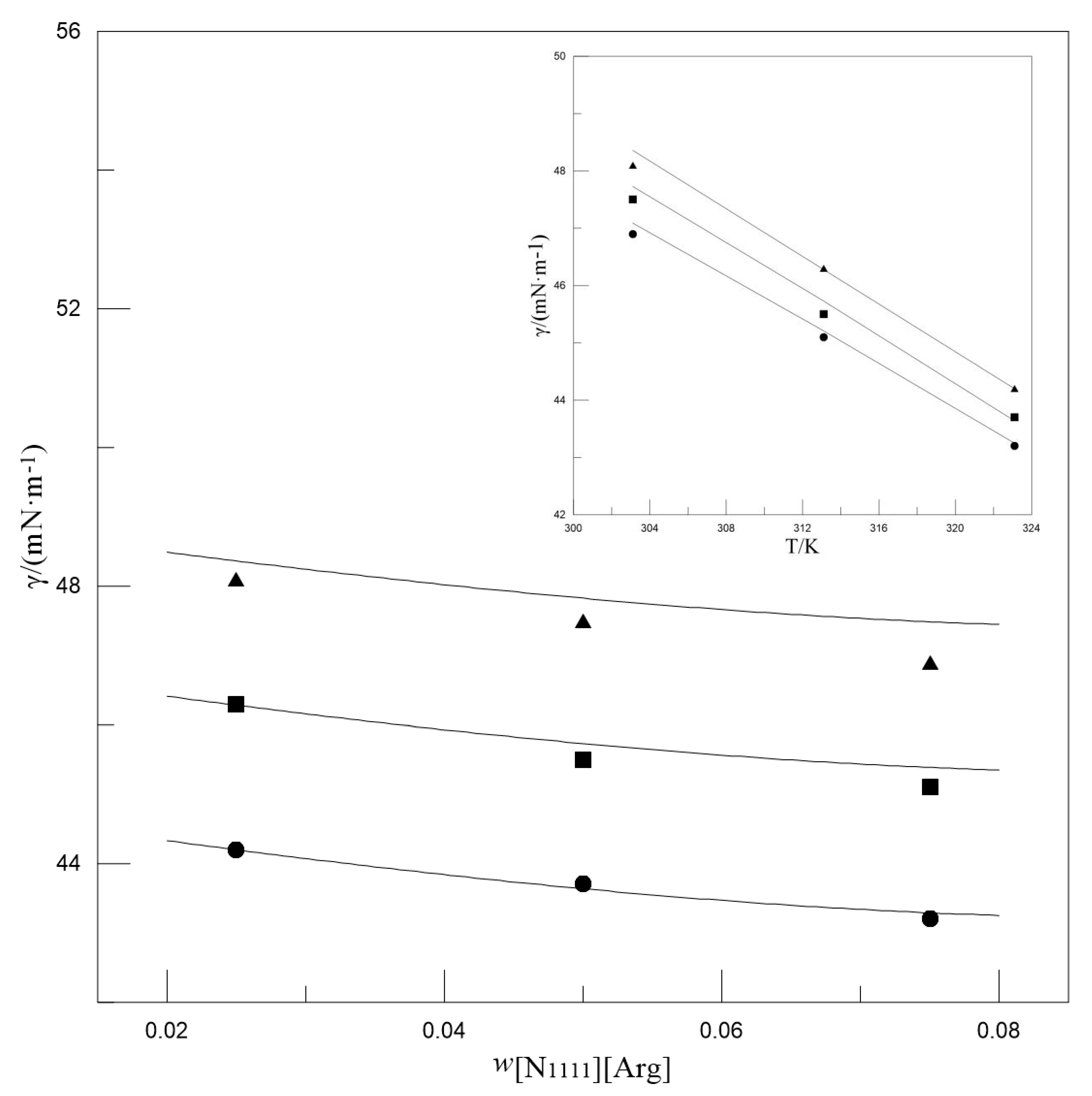
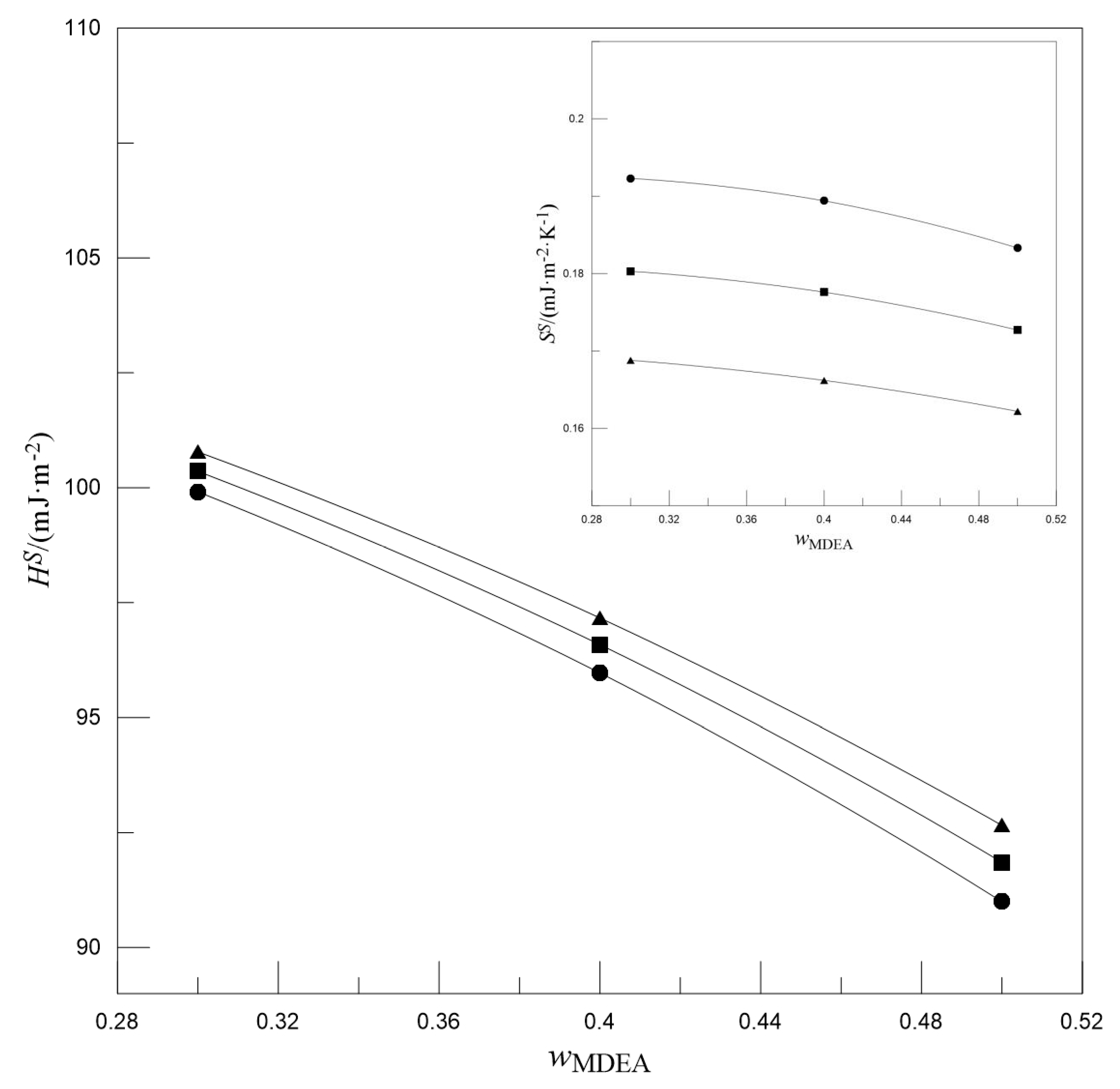
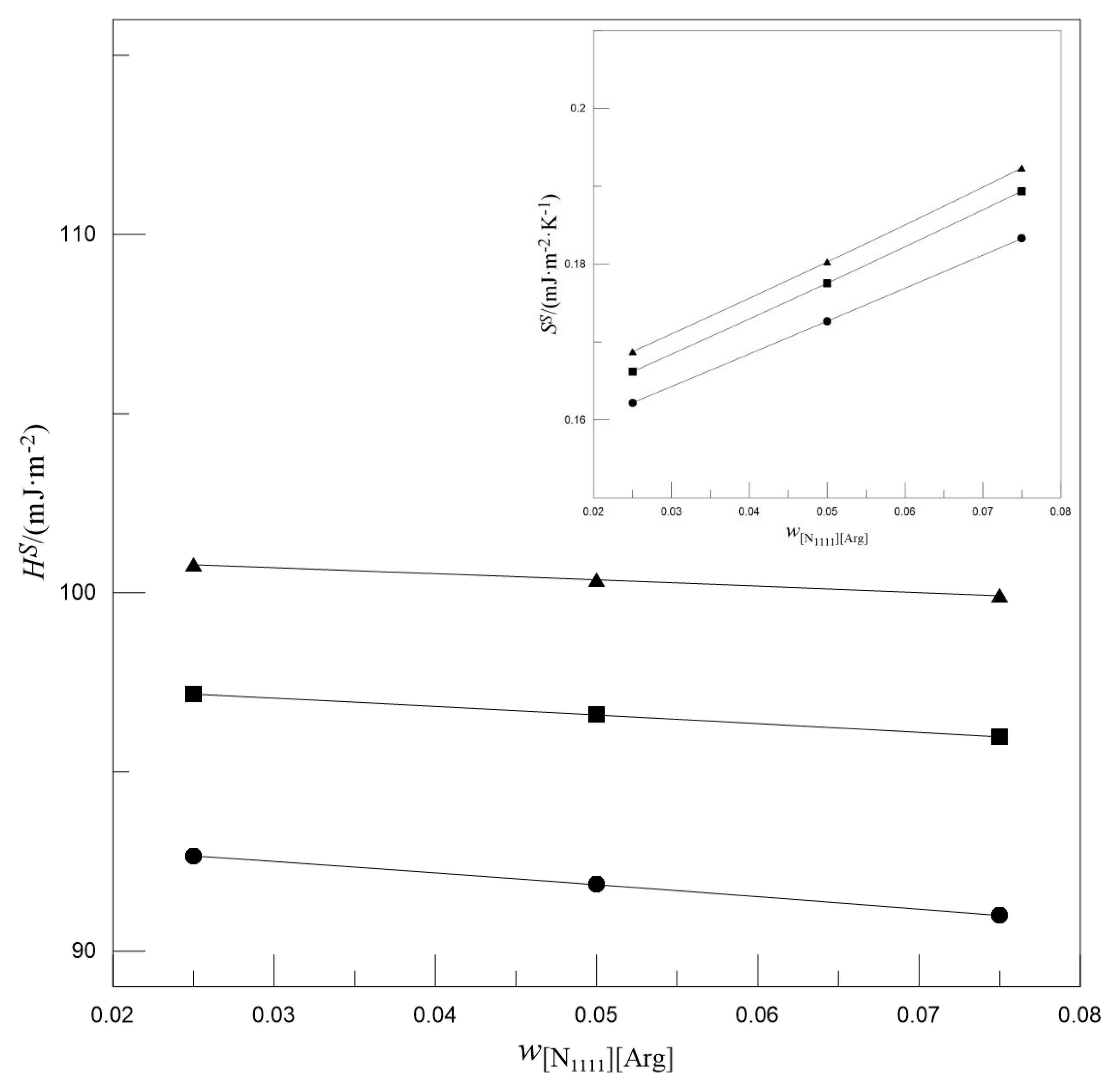
3.1. Surface Tension and Model
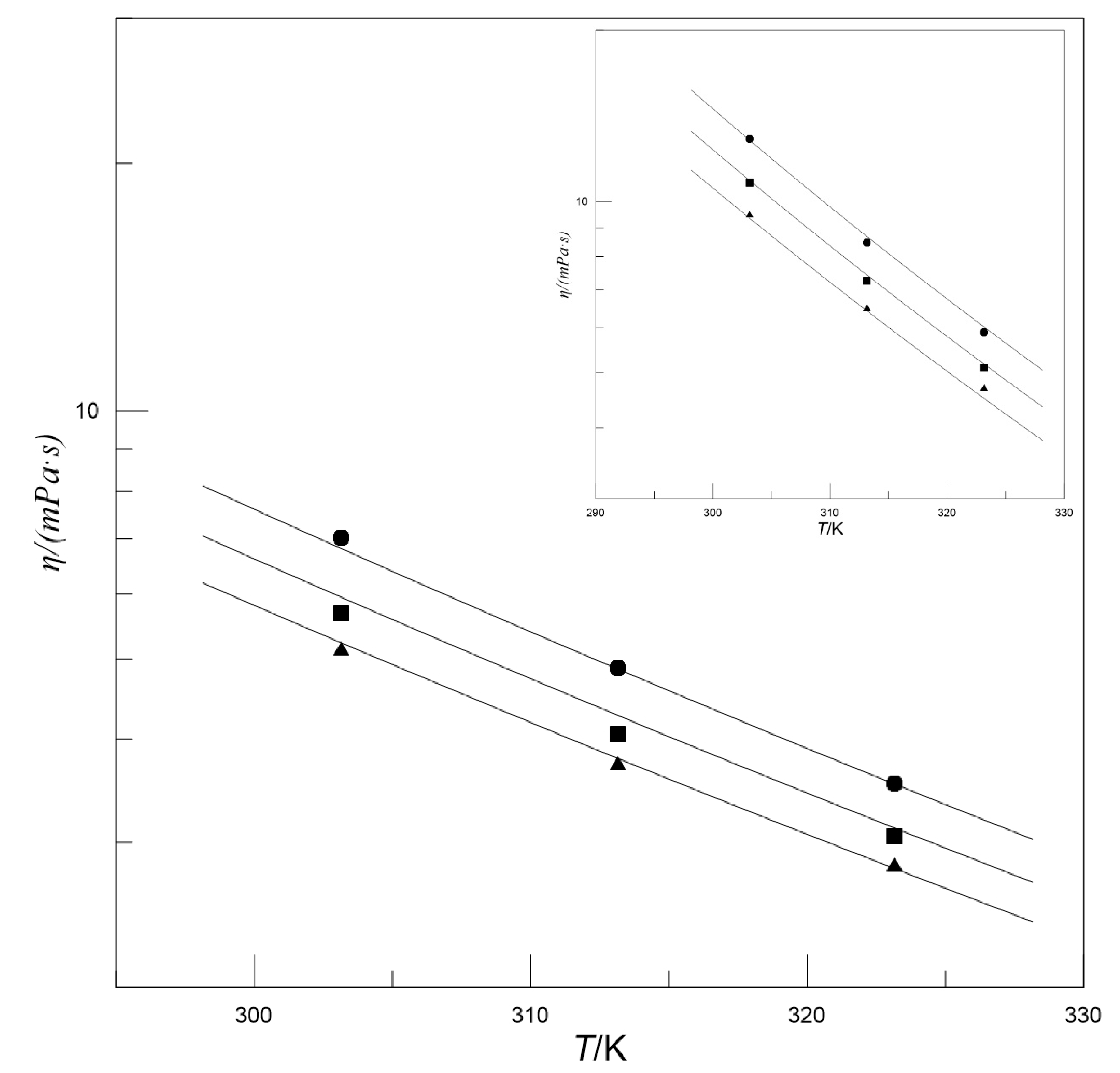
3.2. Viscosity and the Model
4. Conclusions
- The surface tension decreased with the increase in solution mass fraction and temperature. The viscosity increased with the increase in solution mass fraction and decreased with the increase in temperature.
- The thermodynamic models accurately reflected the effects of the solution mass fraction and temperature on the surface tension and viscosity.
- With the increase in wMDEA, both the SS and HS decreased, whereas the SS increased and the HS decreased with the increase in w[N1111][Arg].
- The increase in solution mass fraction can result in the increase in Ea and decrease in DH2S,solu.
Author Contributions
Funding
Conflicts of Interest
References
- Razzaq, R.; Li, C.; Zhang, S. Coke oven gas: Availability, properties, purification, and utilization in China. Fuel 2013, 113, 287–299. [Google Scholar] [CrossRef]
- Bai, Z.; Bai, J.; Li, W. Utilization of coke oven gas in China and its potential for reduction of CO2 emission. Clean Coal Technol. 2016, 22, 90–95. [Google Scholar] [CrossRef]
- Zou, H.; Sheng, M.; Sun, X.; Ding, Z.; Arowo, M.; Luo, Y.; Zhang, L.; Chu, G.; Chen, J.-F.; Sun, B. Removal of hydrogen sulfide from coke oven gas by catalytic oxidative absorption in a rotating packed bed. Fuel 2017, 204, 47–53. [Google Scholar] [CrossRef]
- Kazemi, A.; Malayeri, M.; Kharaji, A.G.; Shariati, A. Feasibility study, simulation and economical evaluation of natural gas sweetening processes—Part 1: A case study on a low capacity plant in Iran. J. Nat. Gas Sci. Eng. 2014, 20, 16–22. [Google Scholar] [CrossRef]
- Abdulrahman, R.; Sebastine, I. Natural gas sweetening process simulation and optimization: A case study of Khurmala field in Iraqi Kurdistan region. J. Nat. Gas Sci. Eng. 2013, 14, 116–120. [Google Scholar] [CrossRef]
- Zhang, L. Application of Desulfurization and Decyanation as Well as Acid Making Technology for Coke Oven Gas in TISCO. Metall. Power 2013, 3, 17–18. [Google Scholar]
- Zhang, P.; Li, M.; Lv, C.; Zhang, Y.; Wang, L.; Fu, D. Effect of partial pressure on CO2 absorption performance in piperazine promoted 2-diethylaminoethanol and 1-dimethylamino-2-propanol aqueous solutions. J. Chem. Thermodyn. 2020, 150, 106198. [Google Scholar] [CrossRef]
- Qian, Z.; Xu, L.-B.; Li, Z.-H.; Li, H.; Guo, K. Selective Absorption of H2S from a Gas Mixture with CO2 by AqueousN-Methyldiethanolamine in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2010, 49, 6196–6203. [Google Scholar] [CrossRef]
- Mandal, B.; Biswas, A.; Bandyopadhyay, S. Selective absorption of H2S from gas streams containing H2S and CO2 into aqueous solutions of N-methyldiethanolamine and 2-amino-2-methyl-1-propanol. Sep. Purif. Technol. 2004, 35, 191–202. [Google Scholar] [CrossRef]
- Lu, J.-G.; Zheng, Y.; He, D.-L. Selective absorption of H2S from gas mixtures into aqueous solutions of blended amines of methyldiethanolamine and 2-tertiarybutylamino-2-ethoxyethanol in a packed column. Sep. Purif. Technol. 2006, 52, 209–217. [Google Scholar] [CrossRef]
- Haghtalab, A.; Afsharpour, A. Solubility of CO2+H2S gas mixture into different aqueous N-methyldiethanolamine solutions blended with 1-butyl-3-methylimidazolium acetate ionic liquid. Fluid Phase Equilibria 2015, 406, 10–20. [Google Scholar] [CrossRef]
- Tian, X.; Wang, L.; Fu, D.; Li, C. Absorption and Removal Efficiency of Low-Partial-Pressure H2S in a Monoethanolamine-Activated N-Methyldiethanolamine Aqueous Solution. Energy Fuels 2018, 33, 629–635. [Google Scholar] [CrossRef]
- Zheng, W.; Wu, D.; Feng, X.; Hu, J.; Zhang, F.; Wu, Y.-T.; Hu, X. Low viscous Protic ionic liquids functionalized with multiple Lewis Base for highly efficient capture of H2S. J. Mol. Liq. 2018, 263, 209–217. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.-L.; Li, Z.-D.; Wei, Y.-N.; Wei, J.-P. CO2/CH4 and H2S/CO2 Selectivity by Ionic Liquids in Natural Gas Sweetening. Energy Fuels 2017, 32, 10–23. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, X.-M.; Zhou, L.-S.; Tao, D.-J.; Fan, J.-P. Highly efficient and selective absorption of H2S in phenolic ionic liquids: A cooperative result of anionic strong basicity and cationic hydrogen-bond donation. Chem. Eng. Sci. 2017, 173, 253–263. [Google Scholar] [CrossRef]
- Jou, F.-Y.; Mather, A.E. Solubility of Hydrogen Sulfide in [bmim][PF6]. Int. J. Thermophys. 2007, 28, 490–495. [Google Scholar] [CrossRef]
- Mortazavi-Manesh, S.; Satyro, M.; Marriott, R.A. Screening ionic liquids as candidates for separation of acid gases: Solubility of hydrogen sulfide, methane, and ethane. AIChE J. 2013, 59, 2993–3005. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, J.-Y.; Hu, X.; Wu, Y.-T. Absorption of H2S and CO2 in Aqueous Solutions of Tertiary-Amine Functionalized Protic Ionic Liquids. Energy Fuels 2017, 31, 14060–14069. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, K.-X.; Meng, Y.-N.; Qi, M.; Geng, J.; Wu, Y.-T.; Zhang, Z.-B. Intensification of dimethyaminoethoxyethanol on CO2 absorption in ionic liquid of amino acid. Int. J. Greenh. Gas Control 2016, 51, 415–422. [Google Scholar] [CrossRef]
- Zhang, X.; Tu, Z.; Li, H.; Huang, K.; Hu, X.; Wu, Y.; Macfarlane, D.R. Selective separation of H2S and CO2 from CH4 by supported ionic liquid membranes. J. Membr. Sci. 2017, 543, 282–287. [Google Scholar] [CrossRef]
- Handy, H.; Santoso, A.; Widodo, A.; Palgunadi, J.; Soerawidjaja, T.H.; Indarto, A. H2S–CO2 Separation Using Room Temperature Ionic Liquid [BMIM][Br]. Sep. Sci. Technol. 2014, 49, 2079–2084. [Google Scholar] [CrossRef]
- Ohno, H.; Fukumoto, K. Amino acid ionic liquids. Acc. Chem. Res. 2007, 40, 1122–1129. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhang, K.; Ren, S.; Hou, Y.; Wu, W. Efficient capture of low partial pressure H2S by tetraethyl ammonium amino acid ionic liquids with absorption-promoted solvents. RSC Adv. 2016, 6, 101462–101469. [Google Scholar] [CrossRef]
- Seyedhosseini, B.; Izadyar, M.; Housaindokht, M.R. A Computational Exploration of H2S and CO2 Capture by Ionic Liquids Based on α-Amino Acid Anion and N7,N9-Dimethyladeninium Cation. J. Phys. Chem. A 2017, 121, 4352–4362. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Wang, L.; Fu, D. Absorption and Removal Efficiency of Low-Partial-Pressure H2S in a Tetramethylammonium Glycinate Activated N-Methyldiethanolamine Aqueous Solution. Energy Fuels 2019, 33, 8413–8422. [Google Scholar] [CrossRef]
- Tariq, M.; Freire, M.G.; Saramago, B.; Coutinho, J.A.P.; Lopes, J.N.C.; Rebelo, L.P.N. Surface tension of ionic liquids and ionic liquid solutions. Chem. Soc. Rev. 2012, 41, 829–868. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Sun, Y.; Zhao, D.; Zhuang, Y.; Wang, R.; Yang, F.; Liu, X.; Chen, Y. Surface tension of binary mixtures of (ionic liquid + tributyl phosphate). J. Chem. Thermodyn. 2019, 132, 214–221. [Google Scholar] [CrossRef]
- Song, D.; Seibert, A.F.; Rochelle, G.T. Effect of liquid viscosity on the liquid phase mass transfer coefficient of packing. Energy Procedia 2014, 63, 1268–1286. [Google Scholar] [CrossRef] [Green Version]
- Song, D.; Seibert, A.F.; Rochelle, G.T. Effect of liquid viscosity on mass transfer area and liquid film mass transfer coefficient for GT-OPTIMPAK 250Y. Energy Procedia 2017, 114, 2713–2727. [Google Scholar] [CrossRef]
- Zuiderweg, F.; Harmens, A. The influence of surface phenomena on the performance of distillation columns. Chem. Eng. Sci. 1958, 9, 89–103. [Google Scholar] [CrossRef]
- Kováts, P.; Thévenin, D.; Zähringer, K. Influence of viscosity and surface tension on bubble dynamics and mass transfer in a model bubble column. Int. J. Multiph. Flow 2020, 123, 103174. [Google Scholar] [CrossRef]
- Wei, C.; Xie, B.; Xiao, H.; Wang, D. Volumetric Mass Transfer Coefficient of Oxygen in an Internal Loop Airlift Reactor with a Convergence-Divergence Draft Tube. Chem. Eng. Technol. 2000, 23, 597–603. [Google Scholar] [CrossRef]
- Wang, L.; Tian, X.; Fu, D.; Du, X.; Ye, J. Experimental investigation on CO2 absorption capacity and viscosity for high concentrated 1-dimethylamino-2-propanol–monoethanolamine aqueous blends. J. Chem. Thermodyn. 2019, 139, 105865. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, L.; Lu, C.; Li, M.; Yu, S.; Fu, D. Experiment and model for surface tensions of 2-diethylaminoethanol-N-(2-aminoethyl)ethanolamine, 2-diethylaminoethanol-N-methyl-1,3-propane-diamine and 2-diethylaminoethanol-1,4-butanediamine aqueous solutions. J. Mol. Liq. 2019, 288, 111031. [Google Scholar] [CrossRef]
- Fu, D.; Wang, L.; Tian, X. Surface thermodynamics of DMA2P, DMA2P-MEA and DMA2P-PZ aqueous solutions. J. Chem. Thermodyn. 2017, 107, 79–84. [Google Scholar] [CrossRef]
- Wang, L.; Tian, X.; Fang, C.; Huang, H.; Fu, D.; Quan, Y. Analysis of Surface Thermodynamics for Amino Acid Ionic Liquid–1-Dimethylamino-2-propanol Aqueous Blends. J. Chem. Eng. Data 2019, 64, 3661–3667. [Google Scholar] [CrossRef]
- Rodríguez, D.M.; Romero, C.M. Surface Tension of Glycine, Alanine, Aminobutyric Acid, Norvaline, and Norleucine in Water and in Aqueous Solutions of Strong Electrolytes at Temperatures from (293.15 to 313.15) K. J. Chem. Eng. Data 2017, 62, 3687–3696. [Google Scholar] [CrossRef]
- Fu, D.; Wang, L.; Tian, X. Experiments and model for the surface tension of DEAE-PZ and DEAE-MEA aqueous solutions. J. Chem. Thermodyn. 2017, 105, 71–75. [Google Scholar] [CrossRef]
- Gliński, J.; Chavepeyer, G.; Platten, J.K. Surface properties of diluted aqueous solutions of solutes containing isopropyl hydrophobic group. J. Chem. Phys. 2001, 114, 5702–5706. [Google Scholar] [CrossRef]
- Maham, Y.; Chevillard, A.; Mather, A.E. Surface Thermodynamics of Aqueous Solutions of Morpholine and Methylmorpholine. J. Chem. Eng. Data 2004, 49, 411–415. [Google Scholar] [CrossRef]
- Yusoff, R.; Aroua, M.K.; Shamiri, A.; Ahmady, A.; Jusoh, N.S.; Asmuni, N.F.; Bong, L.C.; Thee, S.H. Density and viscosity of aqueous mixtures of N-methyldiethanolamines (MDEA) and ionic liquids. J. Chem. Eng. Data 2013, 58, 240–247. [Google Scholar] [CrossRef]
- Ghani, N.A.; Sairi, N.A.; Aroua, M.K.; Alias, Y.; Yusoff, R. Density, Surface Tension, and Viscosity of Ionic Liquids (1-Ethyl-3-methylimidazolium diethylphosphate and 1,3-Dimethylimidazolium dimethylphosphate) Aqueous Ternary Mixtures with MDEA. J. Chem. Eng. Data 2014, 59, 1737–1746. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Zeng, S.; Zhou, Q.; Dong, H.; Tian, X.; Zhang, S. Density, viscosity, and performances of carbon dioxide capture in 16 absorbents of amine + ionic liquid + H2O, ionic liquid + H2O, and amine + H2O systems. J. Chem. Eng. Data 2010, 55, 3513–3519. [Google Scholar] [CrossRef]
- Weiland, R.H.; Dingman, J.C.; Cronin, D.B.; Browning, G.J. Density and viscosity of some partially carbonated aqueous alkanolamine solutions and their blends. J. Chem. Eng. Data 1998, 43, 378–382. [Google Scholar] [CrossRef]
- Wang, L.; Fang, C.; Du, X.; Fu, K.; Tian, X.; Zhang, P.; Fu, D. Surface thermodynamics and viscosity of 1-dimethylamino-2-propanol + 1-(2-aminoethyl)piperazine and 1-dimethylamino-2-propanol + 1,5-diamino-2-methylpentane aqueous solutions. J. Chem. Thermodyn. 2020, 151, 106242. [Google Scholar] [CrossRef]
- Zhao, Z.; Xing, X.; Tang, Z.; Zheng, Y.; Fei, W.; Liang, X.; Ataeivarjovi, E.; Guo, N. Experiment and simulation study of CO2 solubility in dimethyl carbonate, 1-octyl-3-methylimidazolium tetrafluoroborate and their mixtures. Energy 2018, 143, 35–42. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Dong, H.; Zhang, X.; Gao, H.; Zhang, S.; Li, J.; Wang, C. Efficient absorption of ammonia with hydroxyl-functionalized ionic liquids. RSC Adv. 2015, 5, 81362–81370. [Google Scholar] [CrossRef]
- Brown, P.; Gurkan, B.; Hatton, T.A. Enhanced gravimetric CO2 capacity and viscosity for ionic liquids with cyanopyrrolide anion. AIChE J. 2015, 61, 2280–2285. [Google Scholar] [CrossRef]
- Portugal, A.; Marques, A.; Mendes, A. Carbon dioxide absorption kinetics in potassium threonate. Chem. Eng. Sci. 2008, 63, 3493–3503. [Google Scholar] [CrossRef]
- Versteeg, G.F.; Van Swaaij, W.P.M. Solubility and diffusivity of acid gases (carbon dioxide, nitrous oxide) in aqueous alkanolamine solutions. J. Chem. Eng. Data 1988, 33, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Jing, G.; Zhou, L. Characterization and absorption of carbon dioxide into aqueous solution of amino acid ionic liquid [N1111][Gly] and 2-amino-2-methyl-1-propanol. Chem. Eng. J. 2012, 204–206, 235–243. [Google Scholar] [CrossRef]
- Haimour, N.; Sandall, O.C. Molecular diffusivity of hydrogen sulfide in water. J. Chem. Eng. Data 1984, 29, 20–22. [Google Scholar] [CrossRef]
- Tamimi, A.; Rinker, E.B.; Sandall, O.C. Diffusion Coefficients for Hydrogen Sulfide, Carbon Dioxide, and Nitrous Oxide in Water over the Temperature Range 293–368 K. J. Chem. Eng. Data 1994, 39, 330–332. [Google Scholar] [CrossRef]

| Chemical Name | CAS | Purity (Mass Fraction, as Stated by the Supplier) | Source |
|---|---|---|---|
| MDEA | 105-59-9 | ≥0.98 | Aladdin Reagent, Shanghai, China |
| [N1111][Arg] | 1450589-45-3 | ≥0.98 | Shanghai Cheng Jie Chemical Co., Ltd., Shanghai, China |
| water | 7732-18-5 | Electrical resistivity > 15 MΩ cm at T = 298 K | Heal Force ROE-100 apparatus, Shanghai, China |
| wMDEA | w[N1111][Arg] | γ/(mN·m−1) | ||
|---|---|---|---|---|
| T = 303.2 K | T = 313.2 K | T = 323.2 K | ||
| 0.300 | 0.025 | 52.2 | 50.0 | 47.8 |
| 0.050 | 51.8 | 49.5 | 47.5 | |
| 0.075 | 51.5 | 49.2 | 47.2 | |
| 0.400 | 0.025 | 50.1 | 48.2 | 46.1 |
| 0.050 | 49.5 | 47.6 | 45.8 | |
| 0.075 | 49.0 | 47.2 | 45.5 | |
| 0.500 | 0.025 | 47.4 | 45.9 | 43.8 |
| 0.050 | 46.9 | 45.6 | 43.6 | |
| 0.075 | 46.3 | 45.4 | 43.3 | |
| wMDEA | w[N1111][Arg] | η/(mPa·s) | ||
|---|---|---|---|---|
| T = 303.2 K | T = 313.2 K | T = 323.2 K | ||
| 0.300 | 0.025 | 3.10 | 2.35 | 1.87 |
| 0.050 | 3.49 | 2.61 | 2.02 | |
| 0.075 | 4.03 | 2.96 | 2.26 | |
| 0.400 | 0.025 | 5.15 | 3.74 | 2.82 |
| 0.050 | 5.68 | 4.06 | 3.05 | |
| 0.075 | 7.01 | 4.87 | 3.53 | |
| 0.500 | 0.025 | 9.52 | 6.50 | 4.71 |
| 0.050 | 10.80 | 7.26 | 5.10 | |
| 0.075 | 12.90 | 8.47 | 5.89 | |
| wMDEA | w[N1111][Arg] | Ea/(kJ·mol−1) |
|---|---|---|
| 0.300 | 0.025 | 20.6 |
| 0.050 | 22.3 | |
| 0.075 | 23.6 | |
| 0.400 | 0.025 | 24.5 |
| 0.050 | 25.3 | |
| 0.075 | 28.0 | |
| 0.500 | 0.025 | 28.7 |
| 0.050 | 30.6 | |
| 0.075 | 32.0 |
| wMDEA | w[N1111][Arg] | |||
|---|---|---|---|---|
| T = 303.2 K | T = 313.2 K | T = 323.2 K | ||
| 0.300 | 0.025 | 0.72 | 0.91 | 1.13 |
| 0.050 | 0.65 | 0.84 | 1.06 | |
| 0.075 | 0.58 | 0.76 | 0.97 | |
| 0.400 | 0.025 | 0.48 | 0.63 | 0.81 |
| 0.050 | 0.44 | 0.59 | 0.76 | |
| 0.075 | 0.37 | 0.51 | 0.68 | |
| 0.500 | 0.025 | 0.29 | 0.41 | 0.54 |
| 0.050 | 0.26 | 0.37 | 0.51 | |
| 0.075 | 0.23 | 0.33 | 0.45 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Wang, L.; Zhang, P.; Fu, D. Surface Thermodynamics, Viscosity, Activation Energy of N-Methyldiethanolamine Aqueous Solutions Promoted by Tetramethylammonium Arginate. Entropy 2020, 22, 1337. https://doi.org/10.3390/e22121337
Tian X, Wang L, Zhang P, Fu D. Surface Thermodynamics, Viscosity, Activation Energy of N-Methyldiethanolamine Aqueous Solutions Promoted by Tetramethylammonium Arginate. Entropy. 2020; 22(12):1337. https://doi.org/10.3390/e22121337
Chicago/Turabian StyleTian, Xiangfeng, Lemeng Wang, Pan Zhang, and Dong Fu. 2020. "Surface Thermodynamics, Viscosity, Activation Energy of N-Methyldiethanolamine Aqueous Solutions Promoted by Tetramethylammonium Arginate" Entropy 22, no. 12: 1337. https://doi.org/10.3390/e22121337
APA StyleTian, X., Wang, L., Zhang, P., & Fu, D. (2020). Surface Thermodynamics, Viscosity, Activation Energy of N-Methyldiethanolamine Aqueous Solutions Promoted by Tetramethylammonium Arginate. Entropy, 22(12), 1337. https://doi.org/10.3390/e22121337






