Hydrodynamic and Thermodynamic Nonequilibrium Effects around Shock Waves: Based on a Discrete Boltzmann Method
Abstract
:1. Introduction
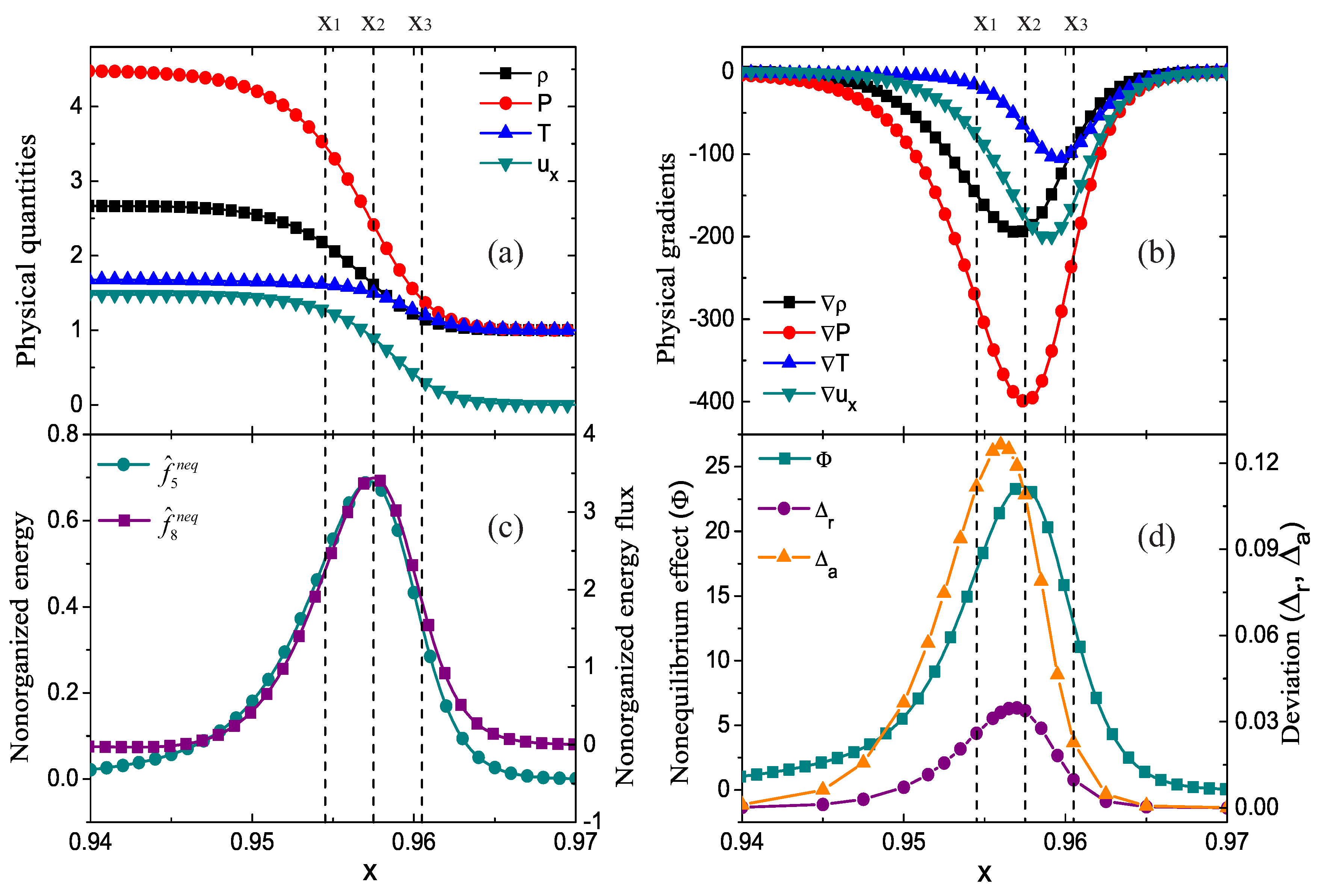
2. Local Nonequilibrium Effects
2.1. Nonequilibrium Manifestations
2.2. Recovery of Velocity Distribution Function
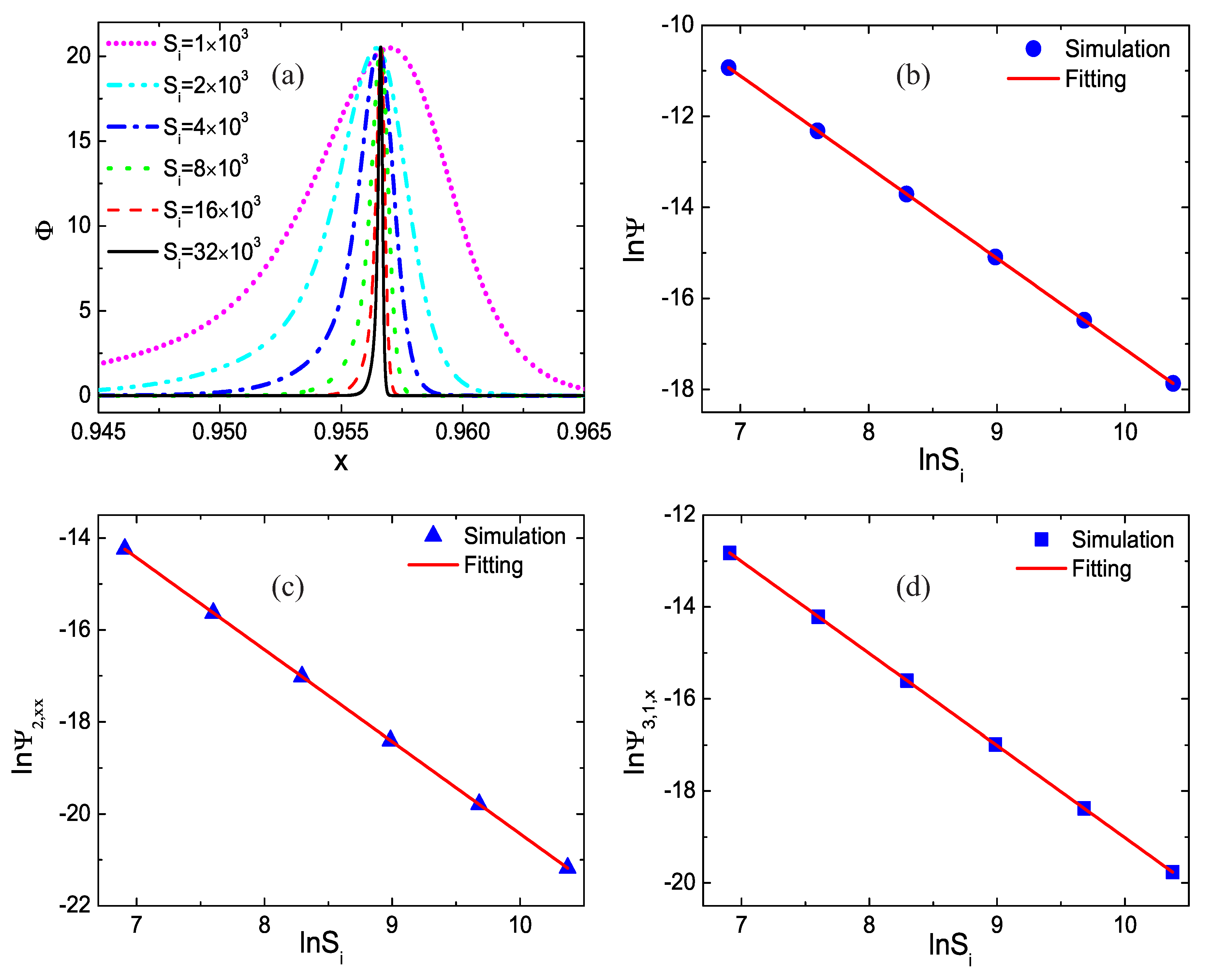
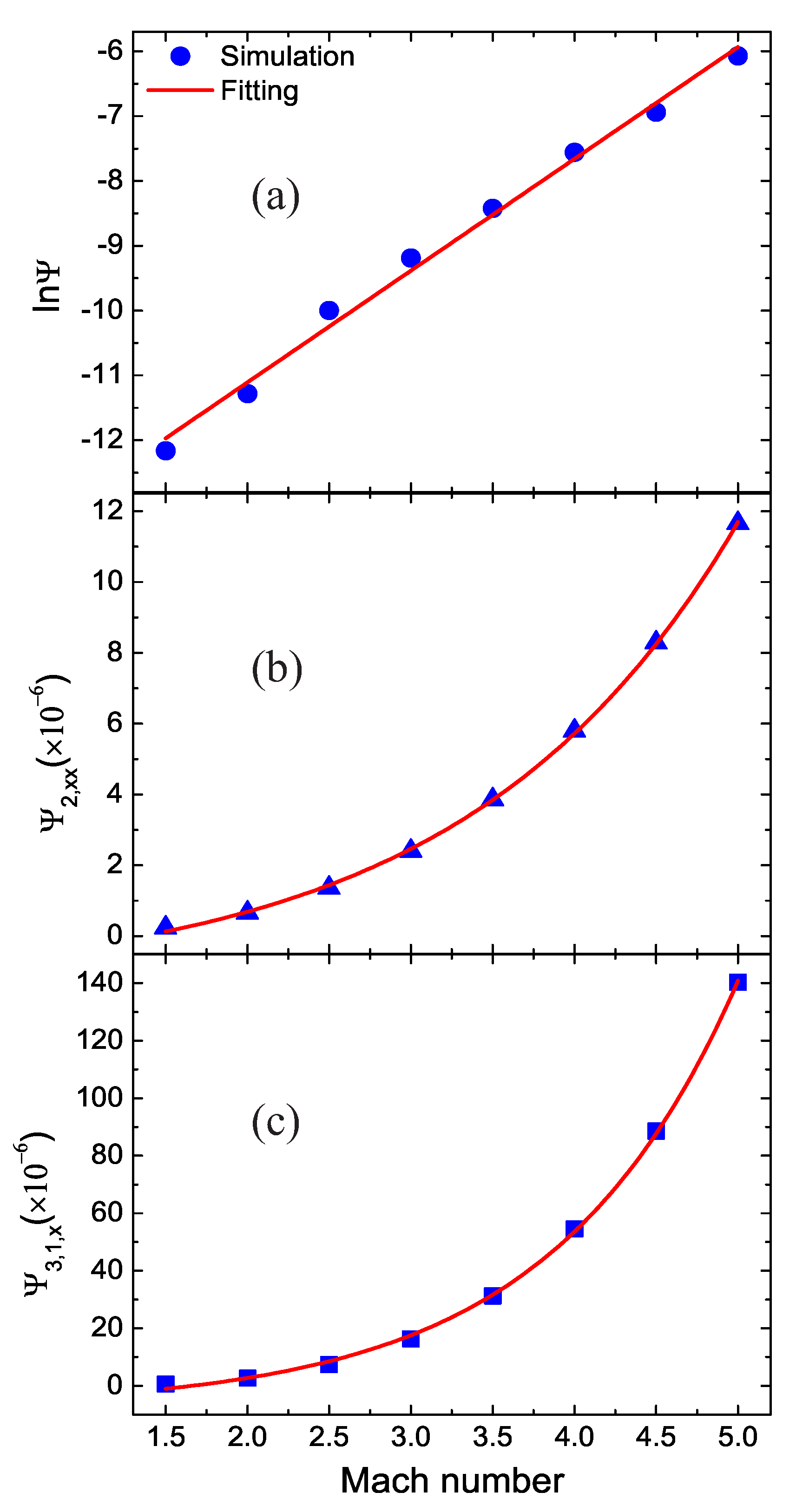
3. Global Nonequilibrium Effects
3.1. Impact of the Relaxation Frequency
3.2. Impact of the Mach Number
3.3. Impact of the Thermal Conductivity
3.4. Impact of the Viscosity
3.5. Impact of the Specific Heat Ratio
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B
References
- Zohuri, B.; Fathi, N. Thermal-Hydraulic Analysis of Nuclear Reactors; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Belov, N.; Konyayev, A.; Korolyov, P.; Kul’kov, S.; Mel’nikov, A.; Platova, T.; Simonenko, V.; Tolkachyov, V.; Khabibullin, M. Modeling of shock-wave compaction of powder ceramics using a ballistic testing unit. J. Appl. Mech. Tech. Phys. 1997, 38, 38–44. [Google Scholar] [CrossRef]
- Smetannikov, A.; Teterev, A. High Temperature Hydrodynamics of Explosion and Shock Wave Phenomena. Nonlinear Phenom. Complex Syst. 2014, 17, 439–444. [Google Scholar]
- Chu, C.; Gross, R. Shock waves in plasma physics. In Advances in Plasma Physics Volume 2; Wiley: Chichester, UK, 1969; pp. 139–202. [Google Scholar]
- Ben-Dor, G.; Igra, O.; Elperin, T. Handbook of Shock Waves, Three Volume Set; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Courant, R.; Friedrichs, K.O. Supersonic Flow and Shock Waves; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Zel’Dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Courier Corporation: North Chelmsford, MA, USA, 2002. [Google Scholar]
- Zhokhov, P.A.; Zheltikov, A.M. Attosecond Shock Waves. Phys. Rev. Lett. 2013, 110, 183903. [Google Scholar] [CrossRef] [PubMed]
- Fomin, N.A. How the term “shock waves” came into being. J. Eng. Phys. Thermophys. 2016, 89, 1047–1065. [Google Scholar] [CrossRef]
- Shapiro, A.H. The Dynamics and Thermodynamics of Compressible Fluid Flow; John Wiley & Sons: Hoboken, NJ, USA, 1953. [Google Scholar]
- Lin, C.; Luo, K.H. MRT discrete Boltzmann method for compressible exothermic reactive flows. Comput. Fluids 2018, 166, 176–183. [Google Scholar] [CrossRef]
- Kawakatsu, T.; Ueda, A. A Molecular Dynamics Study of Relaxation Processes at a Detonation Wave Front. J. Phys. Soc. Jpn. 1988, 57, 2955–2965. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Kang, W.; Zhang, P.; Duan, H.; He, X.T. Molecular dynamics simulation of strong shock waves propagating in dense deuterium, taking into consideration effects of excited electrons. Phys. Rev. E 2017, 95, 023201. [Google Scholar] [CrossRef] [Green Version]
- Brenner, D.; Robertson, D.; Elert, M.; White, C. Detonations at nanometer resolution using molecular dynamics. Phys. Rev. Lett. 1993, 70, 2174–2177. [Google Scholar] [CrossRef]
- Bruno, D.; Longo, S. Monte Carlo simulation of nearly kinematic shock fronts in rarefied gases. Eur. Phys. J. Appl. Phys 2002, 17, 233–241. [Google Scholar] [CrossRef]
- Holian, B.L.; Patterson, C.W.; Mareschal, M.; Salomons, E. Modeling shock waves in an ideal gas: Going beyond the Navier-Stokes level. Phys. Rev. E 1993, 47, R24–R27. [Google Scholar] [CrossRef]
- Uribe, F.J.; Velasco, R.M.; García-Colín, L.S. Burnett Description of Strong Shock Waves. Phys. Rev. Lett. 1998, 81, 2044–2047. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Li, Q.; Luo, K.H.; Kang, Q.J.; He, Y.L.; Chen, Q.; Liu, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef] [Green Version]
- Shadloo, M.S. Numerical simulation of compressible flows by lattice Boltzmann method. Numer. Heat Tranf. A Appl. 2019, 75, 167–182. [Google Scholar] [CrossRef]
- Wilde, D.; Kramer, A.; Reith, D.; Foysi, H. Semi-Lagrangian lattice Boltzmann method for compressible flows. Phys. Rev. E 2020, 101, 053306. [Google Scholar] [CrossRef]
- Pan, L.; Xu, K. A third-order compact gas-kinetic scheme on unstructured meshes for compressible Navier–Stokes solutions. J. Comput. Phys. 2016, 318, 327–348. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhong, C.; Pan, D.; Zhuo, C. A gas-kinetic scheme coupled with SST model for turbulent flows. Comput. Math. Appl. 2019, 78, 1227–1242. [Google Scholar] [CrossRef]
- Xu, K.; Huang, J.C. A unified gas-kinetic scheme for continuum and rarefied flows. J. Comput. Phys. 2010, 229, 7747–7764. [Google Scholar] [CrossRef]
- Liu, C.; Xu, K. A Unified Gas Kinetic Scheme for Continuum and Rarefied Flows V: Multiscale and Multi-Component Plasma Transport. Commun. Comput. Phys. 2017, 22, 1175–1223. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhong, C.; Xu, K. Unified gas-kinetic scheme with multigrid convergence for rarefied flow study. Phys. Fluids 2017, 29, 096102. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Xu, K. Discrete unified gas kinetic scheme for multiscale heat transfer based on the phonon Boltzmann transport equation. Int. J. Heat Mass Transf. 2016, 102, 944–958. [Google Scholar] [CrossRef]
- Zhu, L.; Guo, Z. Application of discrete unified gas kinetic scheme to thermally induced nonequilibrium flows. Comput. Fluids 2019, 193, 103613. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Xu, A.; Zhang, G.; Li, Y.; Succi, S. Polar-coordinate lattice Boltzmann modeling of compressible flows. Phys. Rev. E 2014, 89, 013307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, C.; Xu, A.; Zhang, G.; Li, Y. Polar coordinate lattice Boltzmann kinetic modeling of detonation phenomena. Commun. Theor. Phys. 2014, 62, 737. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Xu, A.; Zhang, G.; Li, Y. Double-distribution-function discrete Boltzmann model for combustion. Combust. Flame 2016, 164, 137–151. [Google Scholar] [CrossRef] [Green Version]
- Lai, H.; Xu, A.; Zhang, G.; Gan, Y.; Ying, Y.; Succi, S. Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows. Phys. Rev. E 2016, 94, 023106. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Luo, K.H.; Fei, L.; Succi, S. A multi-component discrete Boltzmann model for nonequilibrium reactive flows. Sci. Rep. 2017, 7, 14580. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Xu, A.; Zhang, G.; Succi, S. Discrete Boltzmann modeling of multiphase flows: Hydrodynamic and thermodynamic non-equilibrium effects. Soft Matter 2015, 11, 5336–5345. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.D.; Xu, A.G.; Zhang, G.C.; Chen, Z.H.; Wang, P. Discrete ellipsoidal statistical BGK model and Burnett equations. Front. Phys. 2018, 13, 135101. [Google Scholar] [CrossRef] [Green Version]
- Gan, Y.; Xu, A.; Zhang, G.; Zhang, Y.; Succi, S. Discrete Boltzmann trans-scale modeling of high-speed compressible flows. Phys. Rev. E 2018, 97, 053312. [Google Scholar] [CrossRef] [Green Version]
- Xu, A.; Lin, C.; Zhang, G.; Li, Y. Multiple-relaxation-time lattice Boltzmann kinetic model for combustion. Phys. Rev. E 2015, 91, 043306. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Xu, A.; Zhang, G. Viscosity, heat conductivity, and Prandtl number effects in the Rayleigh-Taylor Instability. Front. Phys. 2016, 11, 114703. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.; Luo, K.H. Discrete Boltzmann modeling of unsteady reactive flows with nonequilibrium effects. Phys. Rev. E 2019, 99, 012142. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Luo, K.H. Mesoscopic simulation of nonequilibrium detonation with discrete Boltzmann method. Combust. Flame 2018, 198, 356–362. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, A.; Zhang, G.; Zhu, C.; Lin, C. Kinetic modeling of detonation and effects of negative temperature coefficient. Combust. Flame 2016, 173, 483–492. [Google Scholar] [CrossRef] [Green Version]
- Young, D.F.; Munson, B.R.; Okiishi, T.H.; Huebsch, W.W. A Brief Introduction to Fluid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Tocino, A.; Ardanuy, R. Runge-Kutta methods for numerical solution of stochastic differential equations. J. Comput. Appl. Math. 2002, 138, 219–241. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhuang, F. NND schemes and their applications to numerical simulation of two- and three-dimensional flows. Adv. Appl. Mech. 1991, 29, 193–256. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, A.; Zhang, G.; Chen, Z. Discrete Boltzmann Method with Maxwell-Type Boundary Condition for Slip Flow. Commun. Theor. Phys. 2018, 69, 77. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Su, X.; Zhang, Y. Hydrodynamic and Thermodynamic Nonequilibrium Effects around Shock Waves: Based on a Discrete Boltzmann Method. Entropy 2020, 22, 1397. https://doi.org/10.3390/e22121397
Lin C, Su X, Zhang Y. Hydrodynamic and Thermodynamic Nonequilibrium Effects around Shock Waves: Based on a Discrete Boltzmann Method. Entropy. 2020; 22(12):1397. https://doi.org/10.3390/e22121397
Chicago/Turabian StyleLin, Chuandong, Xianli Su, and Yudong Zhang. 2020. "Hydrodynamic and Thermodynamic Nonequilibrium Effects around Shock Waves: Based on a Discrete Boltzmann Method" Entropy 22, no. 12: 1397. https://doi.org/10.3390/e22121397
APA StyleLin, C., Su, X., & Zhang, Y. (2020). Hydrodynamic and Thermodynamic Nonequilibrium Effects around Shock Waves: Based on a Discrete Boltzmann Method. Entropy, 22(12), 1397. https://doi.org/10.3390/e22121397





