Investigation of Entropy in Two-Dimensional Peristaltic Flow with Temperature Dependent Viscosity, Thermal and Electrical Conductivity
Abstract
:1. Introduction
2. Mathematical Formulation
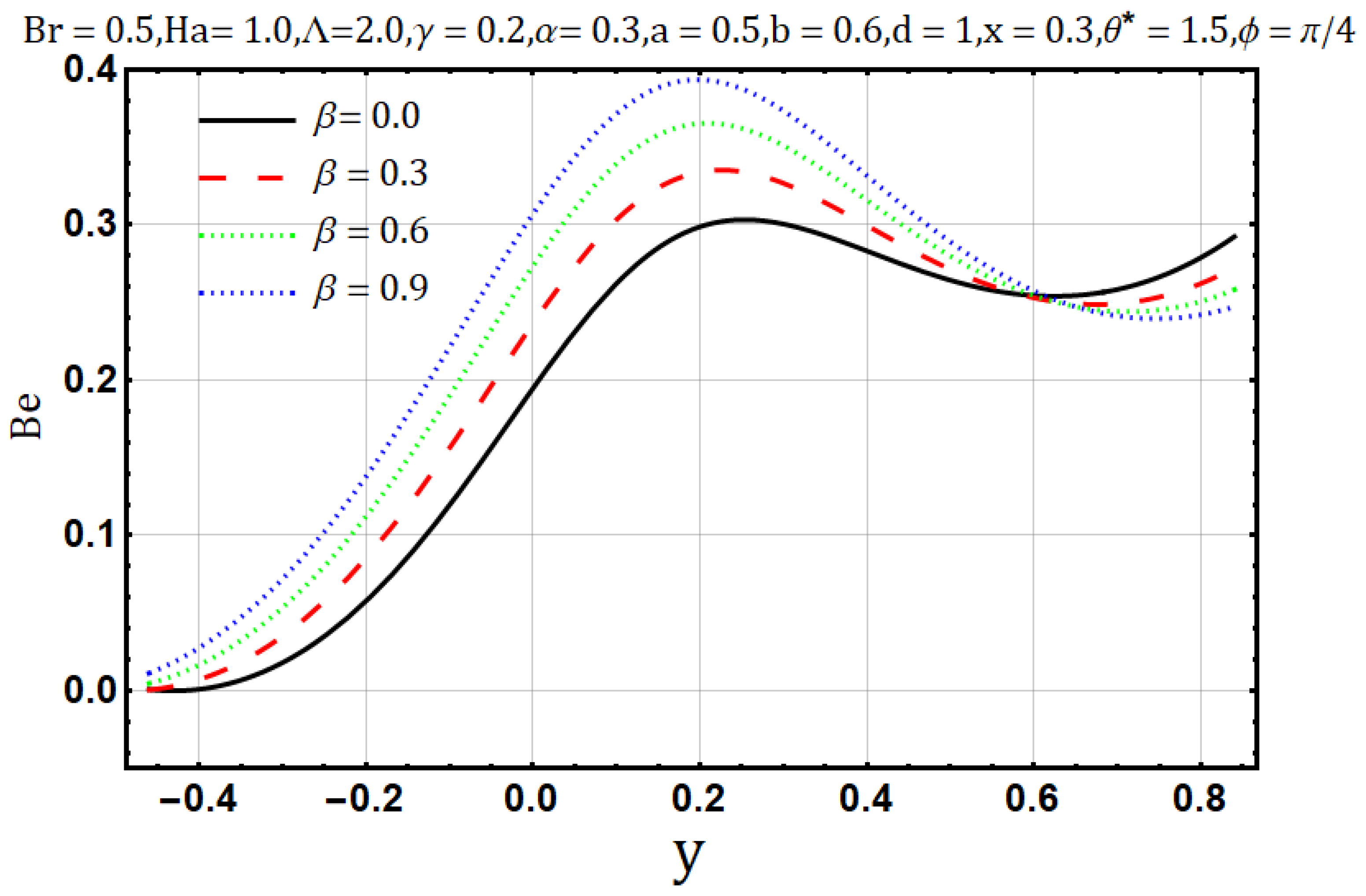
3. Solution Methodology
4. Discussion
5. Conclusions
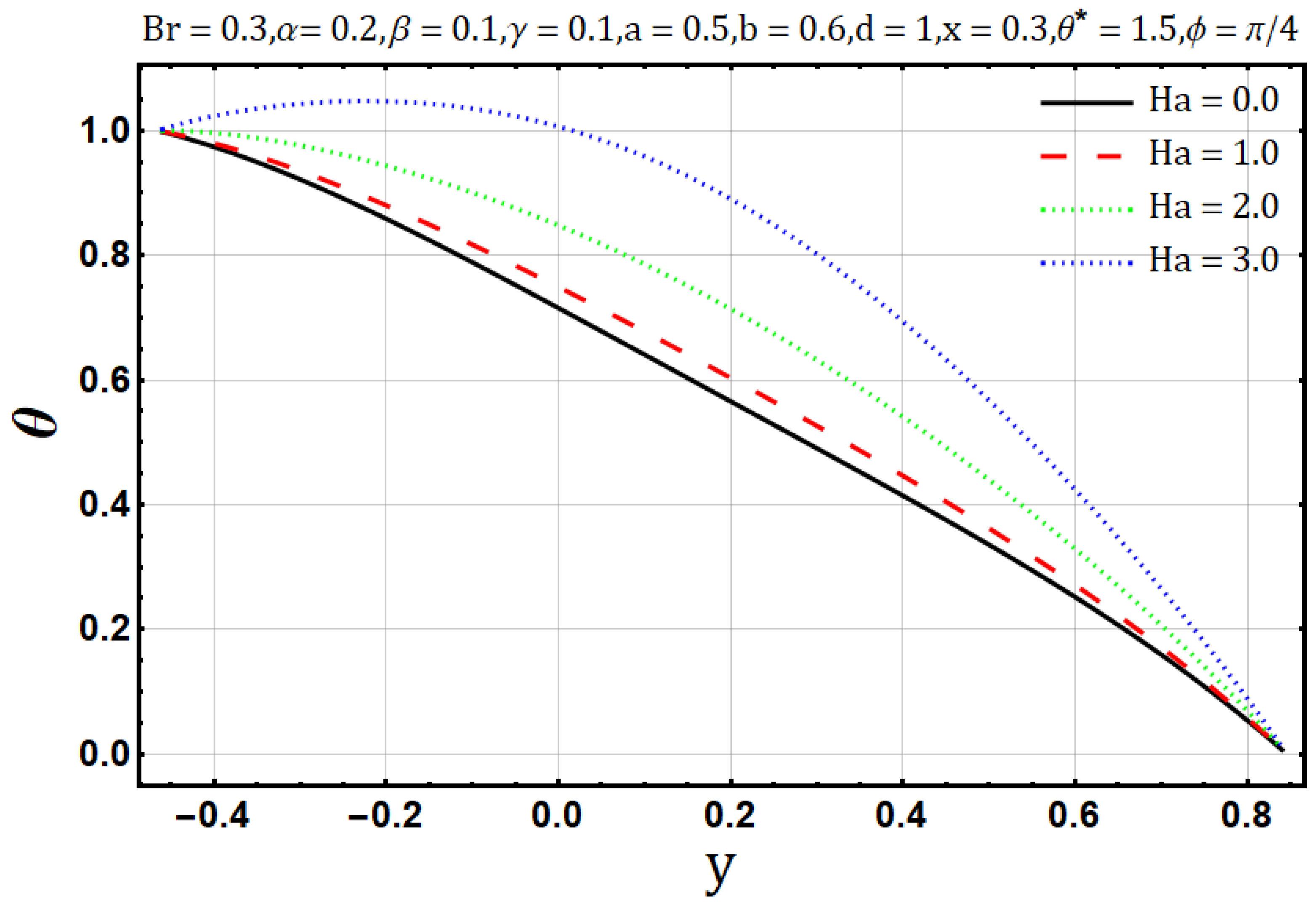
- Fluid flow is observed to reduce when the Hartman number , viscosity parameter and electrical conductivity parameters are enhanced.
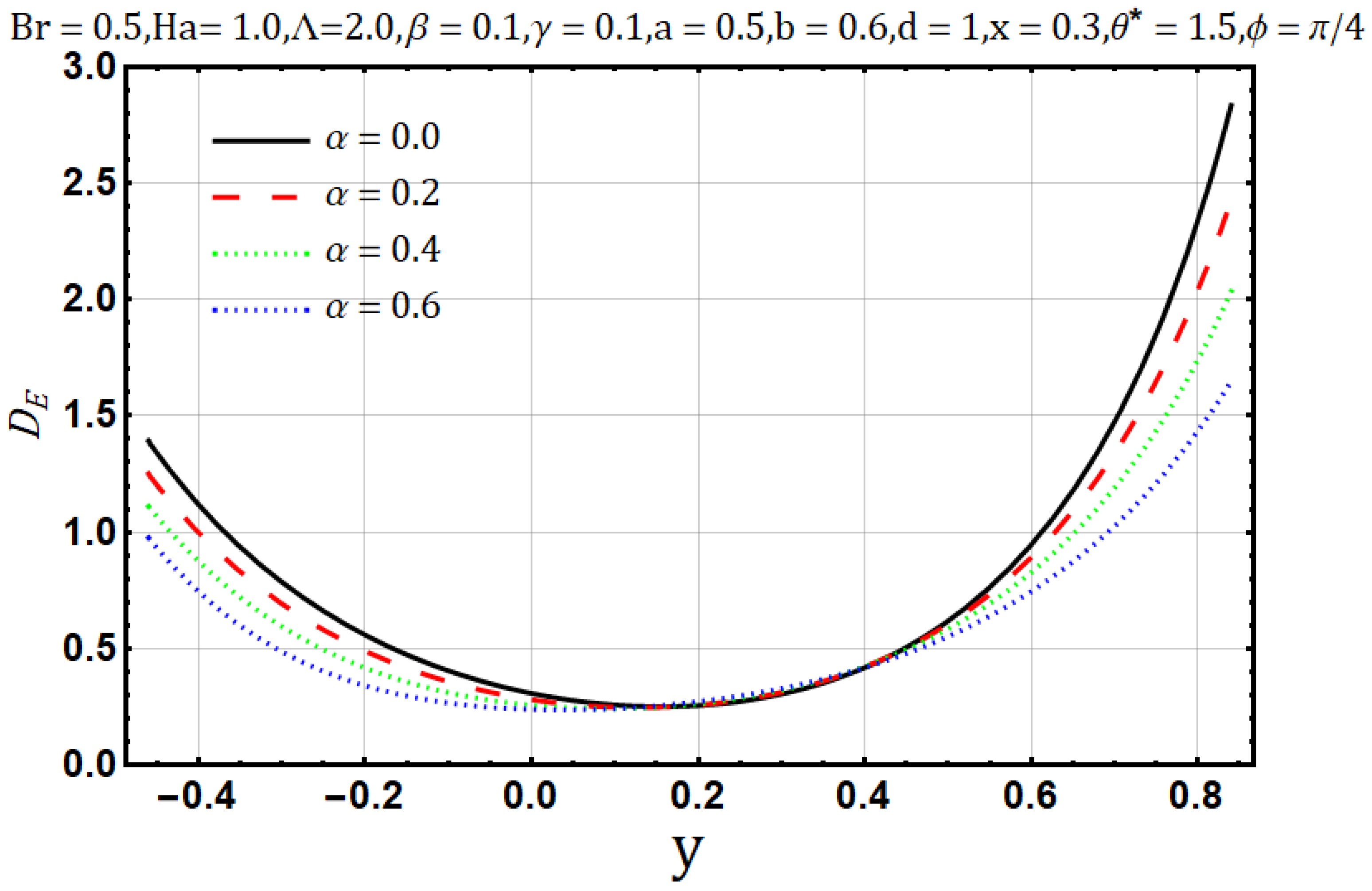
- Heat transfer is reported to behave similarly for variation of Hartman number , electrical conductivity parameters and Brinkman number but it presents opposite behavior in the case of the viscosity parameter .
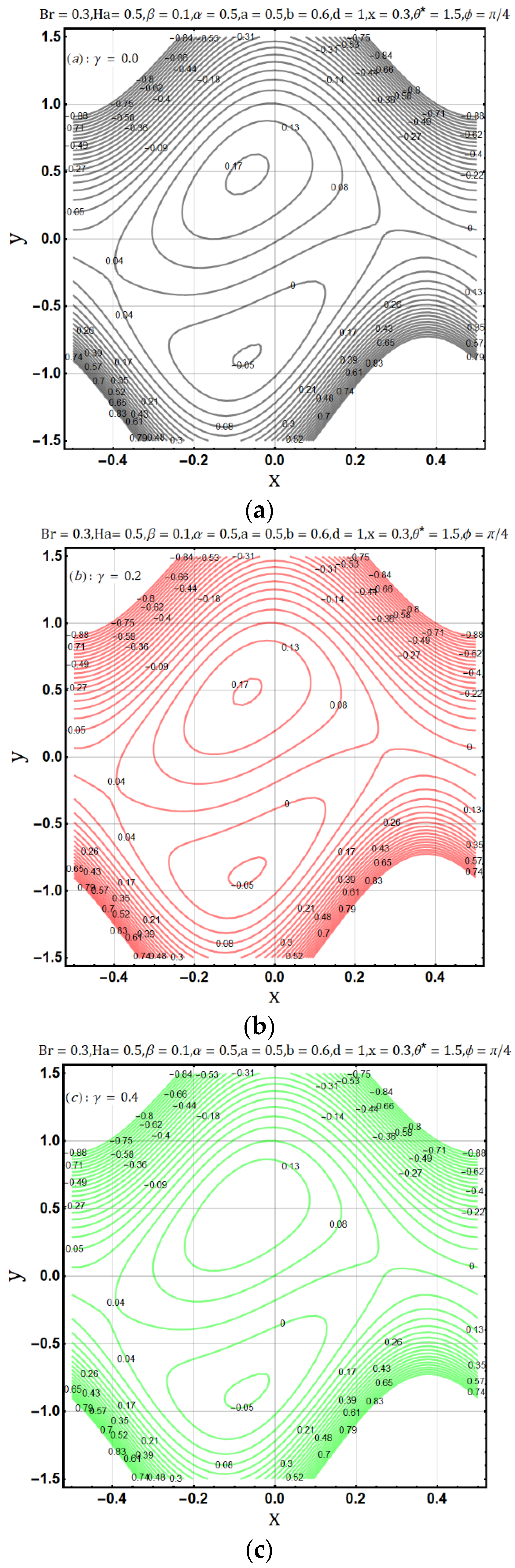
- Entropy generation is amplified by the variation of Hartman number , electrical conductivity parameters and Brinkman number .
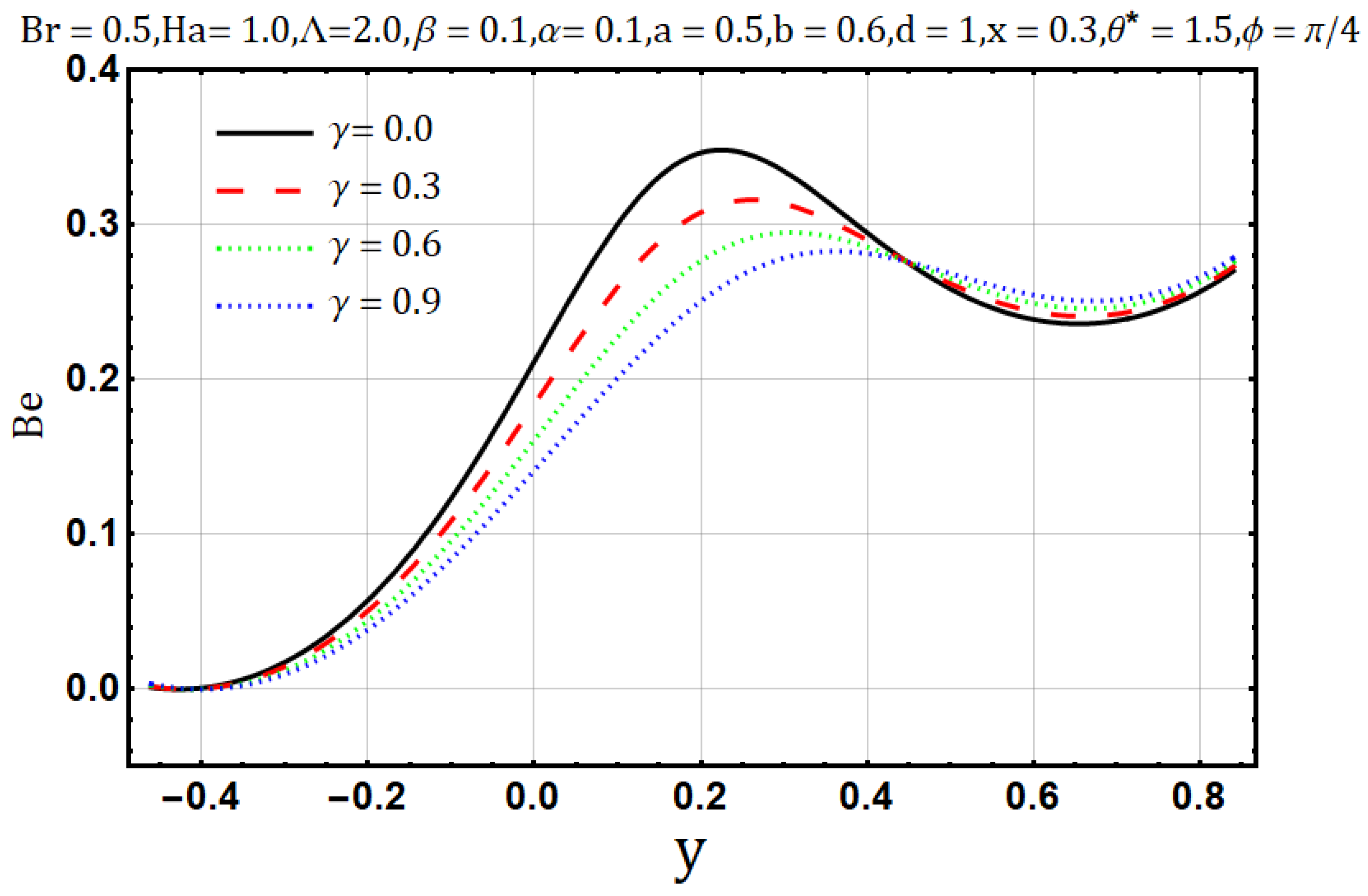
- Bejan number is reduced when Hartman number , electrical conductivity parameters and Brinkman number are enhanced.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Latham, T.W. Fluid Motion in a Peristaltic Pump. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Burns, J.C.; Parkes, T. Peristaltic Motion. J. Fluid Mech. 1967, 29, 731–743. [Google Scholar] [CrossRef]
- Jaffrin, M.Y.; Shapiro, A.H. Peristaltic pumping. Annu. Rev. Fluid Mech. 1971, 3, 13–36. [Google Scholar] [CrossRef]
- Zien, T.F.; Ostrach, S.A. A long wave approximation to peristaltic motion. J. Biomech. 1970, 63, 63–75. [Google Scholar] [CrossRef]
- Vries, K.D.; Lyons, E.A.; Ballard, G.; Levi, C.S.; Lindsay, D.J. Contractions of the inner third of the myometrium. Am. J. Obstet. Gynecol. 1990, 162, 679–682. [Google Scholar] [CrossRef]
- Taylor, G. Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A 1951, 209, 447–461. [Google Scholar]
- Carew, E.O.; Pedley, T.J. An active membrane model for peristaltic pumping: Part-I, Periodic activation waves in an infinite tube. J. Biomech. Eng. 1997, 119, 66–76. [Google Scholar] [CrossRef]
- Shukla, J.B.; Gupta, S.P. Peristaltic Transport of a Power-Law Fluid with Variable Consistency. J. Biomech. Eng. 1982, 104, 182–186. [Google Scholar] [CrossRef]
- Srivastava, L.M.; Srivastava, V.P. Peristaltic transport of blood: Casson model-II. J. Biomech. 1984, 17, 821–829. [Google Scholar] [CrossRef]
- Eytan, O.; Elad, D. Analysis of intra-uterine fluid motion induced by uterine contractions. Bull. Math. Biol. 1999, 61, 221–238. [Google Scholar] [CrossRef]
- Tenforde, T.S. Magnetically induced electric fields and currents in the circulatory system. Prog. Biophys. Mol. Biol. 2008, 87, 279. [Google Scholar] [CrossRef]
- Sud, V.K.; Sekhon, G.S.; Mishra, R.K. Pumping action on blood flow by a magnetic field. Bull. Math. Biol. 1977, 39, 385–390. [Google Scholar] [CrossRef]
- Agarwal, H.L.; Anwaruddin, B. Peristaltic flow of blood in a branch. Ranchi Univ. Math. J. 1984, 15, 111–121. [Google Scholar]
- Mekheimer, K.S. Peristaltic flow of blood under effect of a magnetic field in a nonuniform channels. Appl. Math. Comput. 2004, 153, 763–777. [Google Scholar]
- Hayat, T.; Afsar, A.; Khan, M.; Asghar, S. Peristaltic transport of a third order fluid under the effect of a magnetic field. Comput. Math. Appl. 2007, 53, 1074–1087. [Google Scholar] [CrossRef] [Green Version]
- Elmaboud, Y.A. Influence of induced magnetic field on peristaltic flow in an annulus. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 685–698. [Google Scholar] [CrossRef]
- Noreen, S. Effects of Joule heating and convective boundary conditions on MHD peristaltic flow of couple-stress fluid. J. Heat Transf. 2016, 138, 094502. [Google Scholar] [CrossRef]
- Hayat, T.; Bhatti, Z.A.; Abbasi, F.M.; Ahmad, B.; Alsaedi, A. Effects of variable viscosity and inclined magnetic field on peristaltic motion of fourth-grade fluid with heat transfer. Heat Transf. Res. 2016, 47. [Google Scholar] [CrossRef]
- Noreen, S.; Qasim, M.; Khan, Z.H. MHD pressure driven flow of nanofluid in curved channel. J. Magn. Magn. Mater. 2015, 393, 490–497. [Google Scholar] [CrossRef]
- Noreen, S. Induced magnetic field effects on peristaltic flow in a curved channel. Z. Fur Nat. A 2015, 70, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, F.M.; Hayat, T.; Alsaedi, A.; Ahmed, B. Soret and Dufour effects on peristaltic transport of MHD fluid with variable viscosity. Appl. Math. Inf. Sci. 2014, 8, 211–219. [Google Scholar] [CrossRef] [Green Version]
- Animasaun, I.L.; Oyem, A.O. Effect of variable viscosity, Dufour, Soret and thermal conductivity on free convective heat and mass transfer of non-Darcian flow past porous flat surface. Am. J. Comput. Math. 2014, 4, 357–365. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, L.M.; Srivastava, V.P.; Sinha, S.N. Peristaltic transport of a physiological fluid Part-I Flow in non-uniform geometry. Biorheology 1983, 20, 153. [Google Scholar] [CrossRef]
- El Misery, A.M.; El Hakeem, A.; El Naby, A.; El Nagar, A.H. Effects of a Fluid with Variable Viscosity and an Endoscope on Peristaltic Motion. J. Phys. Soc. Jpn. 2003, 72, 89–93. [Google Scholar] [CrossRef]
- El Hakeem, A.; El Naby, A.; El Misery, A.E.M.; El Shamy, I.I. Hydromagnetic flow of fluid with variable viscosity in a uniform tube with peristalsis. J. Phys. A Math. Gen. 2003, 36, 8535. [Google Scholar]
- Ali, N.; Hussain, Q.; Hayat, T.; Asghar, S. Slip effects on the peristaltic transport of MHD fluid with variable viscosity. Phys. Lett. A 2008, 372, 1477–1489. [Google Scholar] [CrossRef]
- El Hakeem, A.; El Naby, A.; El Misery, A.M.; El Shamy, I.I. Effects of an endoscope and fluid with variable viscosity on peristaltic motion. Appl. Math. Comput. 2004, 158, 497. [Google Scholar]
- Hussain, Q.; Hayat, T.; Asghar, S.; Alsaadi, F. Heat and mass transfer analysis in variable viscosity peristaltic flow with hall current and ion-slip. J. Mech. Med. Biol. 2016, 16, 1650047. [Google Scholar] [CrossRef]
- Reddy, M.S.; Reddy, M.V.V.; Reddy, B.J.; Krishna, S.R. Peristaltic pumping of Jeffery fluid with variable viscosity in a tube under the effect of magnetic field. J. Math. Comput. Sci. 2012, 2, 907–925. [Google Scholar]
- Hayat, T.; Abbasi, F.M. Variable viscosity effects on the peristaltic motion of a third order fluid. Int. J. Numer. Methods Fluids 2011, 67, 1500–1515. [Google Scholar] [CrossRef]
- Reddy, M.V.S.; Reddy, D.P. Peristaltic pumping of a Jeffrey fluid with variable viscosity through a porous medium in a planar channel. Int. J. Math. Arch. 2010, 1, 42–54. [Google Scholar]
- Hussain, Q.; Asghar, S.; Hayat, T.; Alsaedi, A. Peristaltic transport of hydromagnetic Jeffrey fluid with temperature dependent viscosity and thermal conductivity. Int. J. Biomath. 2016, 9, 1650029. [Google Scholar] [CrossRef]
- Hussain, Q.; Asghar, S.; Hayat, T.; Alsaedi, A. Heat transfer analysis in peristaltic flow of MHD Jeffrey fluid with variable thermal conductivity. Appl. Math. Mech. 2015, 36, 499–516. [Google Scholar] [CrossRef]
- Mekheimer, K.H.S.; Elmaboud, A.Y. Simultaneous effects of variable viscosity and thermal conductivity on peristaltic flow in a vertical asymmetric channel. Can. J. Phys. 2014, 92, 1541–1555. [Google Scholar] [CrossRef]
- Hayat, T.; Abbasi, F.M.; Ahmad, B.; Alsaedi, A. MHD mixed convection peristaltic flow with variable Viscosity and thermal conductivity. Sains Malays. 2014, 43, 1583–1590. [Google Scholar]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef] [Green Version]
- Abbassi, H. Entropy generation analysis in a uniformly heated microchannel heat sink. Energy 2007, 32, 1932–1947. [Google Scholar] [CrossRef]
- Abu-Hijleh, B.A.K. Natural Convection Heat Transfer and Entropy Generation from a Horizontal Cylinder with Baffles. ASME J. Heat Transf. 2000, 122, 679–692. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Shafie, S.; Alshomrani, A.S. Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet. Entropy 2017, 19, 10. [Google Scholar] [CrossRef] [Green Version]
- Afridi, M.I.; Qasim, M.; Shafie, S. Entropy generation in hydromagnetic boundary flow under the effects of frictional and Joule heating: Exact solutions. Eur. Phys. J. Plus 2017, 132, 404. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of nonlinear Rosseland radiation. Int. J. Therm. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Khan, I.; Al-Mdallal, Q.M. Analysis of Entropy Generation in Flow of Methanol-Based Nanofluid in a Sinusoidal Wavy Channel. Entropy 2017, 19, 490. [Google Scholar] [CrossRef]
- Noreen, S.; Ain, Q.U. Entropy generation analysis on electroosmotic flow in non-Darcy porous medium via peristaltic pumping. J. Therm. Anal. Calorim. 2019, 137, 1991–2006. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Maraj, E.N.; Nadeem, S. Theoretical analysis of entropy generation in peristaltic transport of nanofluid in an asymmetric channel. Int. J. Exergy 2016, 20, 294–317. [Google Scholar] [CrossRef]
- Munawar, S.; Saleem, N. Second law analysis in the peristaltic flow of variable viscosity fluid. Int. J. Exergy 2016, 20, 170–185. [Google Scholar]
- Narla, V.K.; Prasad, K.M.; Murthy, J.V.R. Second-Law Analysis of the Peristaltic Flow of an Incompressible Viscous Fluid in a Curved Channel. J. Eng. Phys. Thermophys. 2016, 89, 441. [Google Scholar] [CrossRef]
- Hayat, T.; Sadaf, N.; Ahmed, A.; Maimona, R. Analysis of entropy generation in mixed convective peristaltic flow of nanofluid. Entropy 2016, 18, 355. [Google Scholar] [CrossRef] [Green Version]
- Ranjit, K.; Shit, G.C. Entropy generation on electro-osmotic flow pumping by a uniform peristaltic wave under magnetic environment. Energy 2017, 128, 649–660. [Google Scholar] [CrossRef]
- Attia, H.A. Steady MHD Couette flow with temperature-dependent physical properties. Arch. Appl. Mech. 2006, 75, 268. [Google Scholar] [CrossRef]
- Muhammad, T.; Hayat, T.; Alsaedi, A.; Qayyum, A. Hydromagnetic unsteady squeezing flow of Jeffrey fluid between two parallel plates. Chin. J. Phys. 2017, 55, 1511–1522. [Google Scholar] [CrossRef]
- Aziz, A.; Alsaedi, A.; Muhammad, T.; Hayat, T. Numerical study for heat generation/absorption in flow of nanofluid by a rotating disk. Results Phys. 2018, 8, 785–792. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.A.M.; Muhammad, T. Numerical Study for Darcy—Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius Activation Energy. Mathematics 2019, 7, 921. [Google Scholar] [CrossRef] [Green Version]
- Kierzenka, J.; Shampine, L.F. A BVP solver based on residual control and the MATLAB PSE. ACM Trans. Math. Softw. 2001, 27, 299–316. [Google Scholar] [CrossRef]
- Srinivas, S.; Kothandapani, M. Peristaltic transport in an asymmetric channel with heat transfer—A note. Int. Commun. Heat Mass Transf. 2008, 35, 514–522. [Google Scholar] [CrossRef]
















| [56] | [56] | [56] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | −2.0 | 2.0 | 1.0 | 1.0586 | 1.0586 | 1.4556 | 1.4556 | 1.7596 | 1.7596 |
| 0.7 | −2.0 | 2.0 | 1.0 | 1.5418 | 1.5418 | 2.0650 | 2.0650 | 2.6909 | 2.6909 |
| 0.9 | −2.0 | 2.0 | 1.0 | 2.0542 | 2.0542 | 2.6953 | 2.6953 | 3.8524 | 3.8524 |
| 1.1 | −2.0 | 2.0 | 1.0 | 2.5920 | 2.5920 | 3.3484 | 3.3484 | 5.3457 | 5.3457 |
| 0.5 | −0.5 | 2.0 | 3.0 | 8.9333 | 8.9333 | 15.9061 | 15.9061 | 17.4565 | 17.4565 |
| 0.5 | −1.0 | 2.0 | 3.0 | 5.9373 | 5.9373 | 9.1554 | 9.1554 | 7.6982 | 7.6982 |
| 0.5 | −1.5 | 2.0 | 3.0 | 3.6075 | 3.6075 | 4.4727 | 4.4727 | 2.5390 | 2.5390 |
| 0.5 | −2.0 | 2.0 | 3.0 | 1.9440 | 1.9440 | 1.8582 | 1.8582 | 1.9789 | 1.9789 |
| 0.5 | −2.0 | 0.0 | 3.0 | 1.8449 | 1.8449 | 1.8352 | 1.8352 | 1.9738 | 1.9738 |
| 0.5 | −2.0 | 2.0 | 3.0 | 1.9440 | 1.9440 | 1.8582 | 1.8582 | 1.9789 | 1.9789 |
| 0.5 | −2.0 | 3.0 | 3.0 | 2.1353 | 2.1353 | 1.9120 | 1.9120 | 1.9932 | 1.9932 |
| 0.5 | −2.0 | 4.0 | 3.0 | 2.3848 | 2.3848 | 1.9920 | 1.9920 | 2.0182 | 2.0182 |
| 0.5 | −2.0 | 2.0 | 1.0 | 1.0586 | 1.0586 | 1.4556 | 1.4556 | 1.7596 | 1.7596 |
| 0.5 | −2.0 | 2.0 | 2.0 | 1.5013 | 1.5013 | 1.6569 | 1.6569 | 1.8692 | 1.8692 |
| 0.5 | −2.0 | 2.0 | 3.0 | 1.9440 | 1.9440 | 1.8582 | 1.8582 | 1.9789 | 1.9789 |
| 0.5 | −2.0 | 2.0 | 4.0 | 2.3868 | 2.3868 | 2.0595 | 2.0595 | 2.0885 | 2.0885 |
| Parameters | ||||||
|---|---|---|---|---|---|---|
| NDSolve | bvp4c | |||||
| 0.0 | 0.3 | 0.2 | 0.1 | 0.1 | 3.69812 | 3.69811 |
| 1.0 | 0.3 | 0.2 | 0.1 | 0.1 | 3.93678 | 3.93676 |
| 2.0 | 0.3 | 0.2 | 0.1 | 0.1 | 4.65001 | 4.65001 |
| 0.5 | 0.0 | 0.2 | 0.1 | 0.1 | 2.37393 | 2.37393 |
| 0.5 | 0.1 | 0.2 | 0.1 | 0.1 | 2.83928 | 2.83928 |
| 0.5 | 0.3 | 0.2 | 0.1 | 0.1 | 3.30056 | 3.30057 |
| 0.5 | 0.3 | 0.0 | 0.1 | 0.1 | 3.91107 | 3.91107 |
| 0.5 | 0.3 | 0.2 | 0.1 | 0.1 | 3.75783 | 3.75783 |
| 0.5 | 0.3 | 0.4 | 0.1 | 0.1 | 3.59546 | 3.59544 |
| 0.5 | 0.3 | 0.3 | 0.0 | 0.1 | 3.71009 | 3.71007 |
| 0.5 | 0.3 | 0.3 | 0.1 | 0.1 | 3.67806 | 3.67803 |
| 0.5 | 0.3 | 0.3 | 0.2 | 0.1 | 3.64911 | 3.64898 |
| 0.5 | 0.3 | 0.4 | 0.2 | 0.0 | 3.56551 | 3.56549 |
| 0.5 | 0.3 | 0.4 | 0.2 | 0.3 | 3.57507 | 3.57504 |
| 0.5 | 0.3 | 0.4 | 0.2 | 0.6 | 3.58466 | 3.58463 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasim, M.; Ali, Z.; Farooq, U.; Lu, D. Investigation of Entropy in Two-Dimensional Peristaltic Flow with Temperature Dependent Viscosity, Thermal and Electrical Conductivity. Entropy 2020, 22, 200. https://doi.org/10.3390/e22020200
Qasim M, Ali Z, Farooq U, Lu D. Investigation of Entropy in Two-Dimensional Peristaltic Flow with Temperature Dependent Viscosity, Thermal and Electrical Conductivity. Entropy. 2020; 22(2):200. https://doi.org/10.3390/e22020200
Chicago/Turabian StyleQasim, Muhammad, Zafar Ali, Umer Farooq, and Dianchen Lu. 2020. "Investigation of Entropy in Two-Dimensional Peristaltic Flow with Temperature Dependent Viscosity, Thermal and Electrical Conductivity" Entropy 22, no. 2: 200. https://doi.org/10.3390/e22020200





