Robust Power Optimization for Downlink Cloud Radio Access Networks with Physical Layer Security
Abstract
:1. Introduction
2. System Model and Problem Formulation
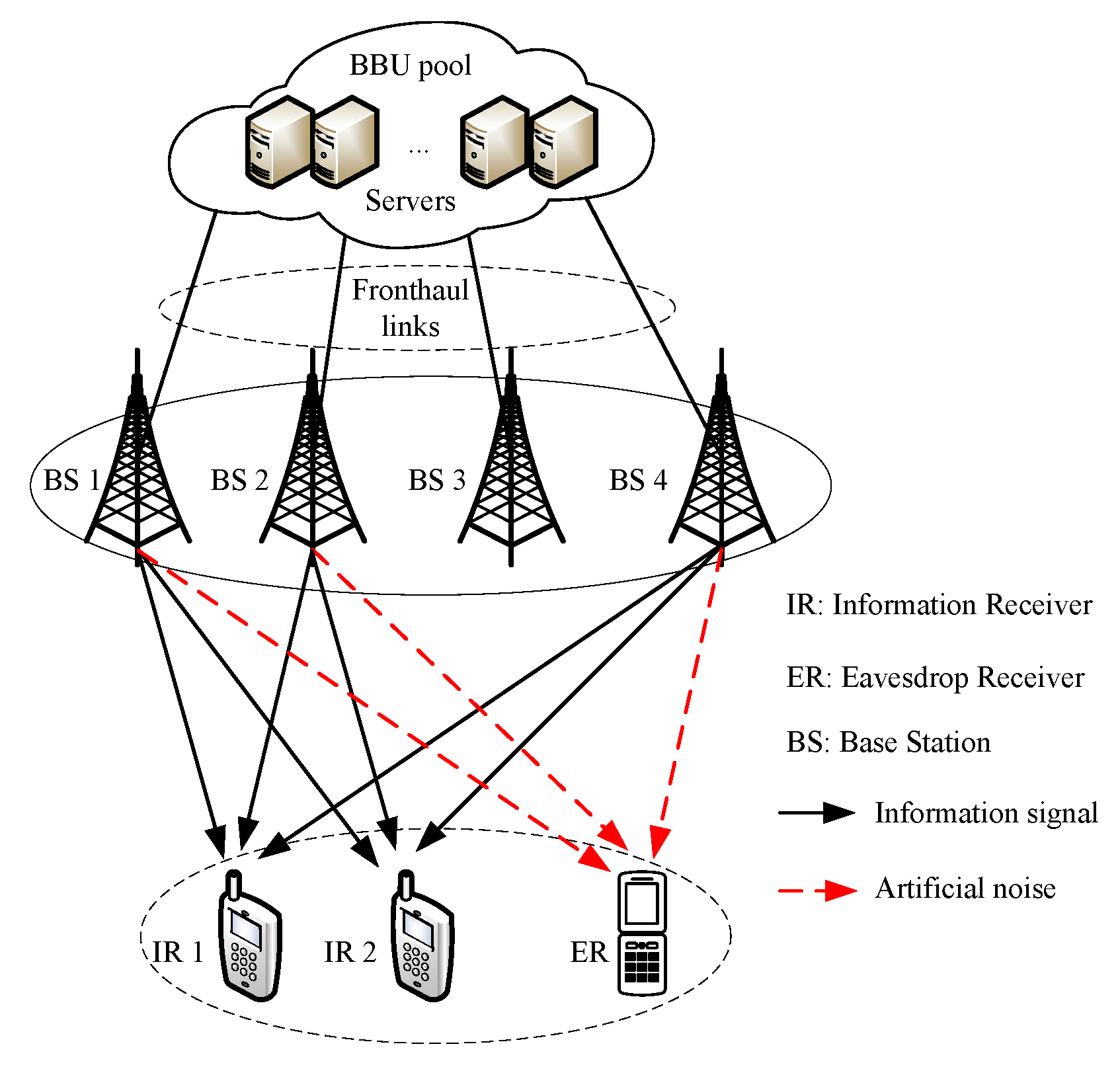
2.1. System Model
2.1.1. Signal Model
2.1.2. Channel Model
2.1.3. Power Model
2.2. Problem Formulation
3. DC-Based Sparse Beamforming Design
3.1. Problem Reformulation
3.1.1. Sparse Beamforming Problem
3.1.2. Smooth -Norm Approximation
3.2. Generalized IDC Procedure
3.2.1. IDC Procedure
3.2.2. Updating Rule of
4. Proposed Optimization Algorithm
4.1. Stage 1: IDC-Based SDP Algorithm
| Algorithm 1 IDC-based SDP algorithm. |
| Initialization: Set the initial values for by letting be a feasible point to problem ; Repeat: Step 1: Fix , solve problem and return instantaneous optimal solution ; Step 2: Update , update using . Until convergence or maximum iteration is reached. |
4.2. Stage 2: Post Processing Procedure
4.3. Stage 3: Transmit Power Optimization
| Algorithm 2 Post processing procedure for finding the final active BSs. |
| Initialization: let , the network power consumption and the iteration index . Step 1: Update the iteration number . Step 2: Let , and solve problem . Step 3: If problem is infeasible, go to Step 5; Otherwise, go to Step 4. Step 4: If , go to Step 1; Otherwise, go to Step 5. Step 5: Obtain the final active BS set . Step 6: Solve problem and obtain the final network power consumption , beamforming and AN (i.e., ). |
4.4. Initialization and Complexity Analysis
4.4.1. Initialization
4.4.2. Complexity Analysis
5. Simulation Results and Discussion
5.1. Power Distribution of the BSs
5.2. Convergence Analysis
5.3. Impact of SINR Threshold of IR on Performance
5.4. Impact of SINR Threshold of ER on Performance
5.5. Performance of the Proposed Algorithm
5.5.1. Impact of BS Antennas on Performance
5.5.2. Impact of CSI Error Radius of ERs on Performance
5.5.3. Network Power Consumption versus ER Number
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Proposition 1
References
- Chen, K.; Duan, R. C-RAN the road towards green RAN. China Mobile Research Institute, White Paper. 2011. Available online: https://pdfs.semanticscholar.org/eaa3/ca62c9d5653e4f2318aed9ddb8992a505d3c.pdf (accessed on 13 February 2020).
- Peng, M.; Li, Y.; Jiang, J.; Li, J.; Wang, C. Heterogeneous cloud radio access networks: A new perspective for enhancing spectral and energy efficiencies. IEEE Wirel. Commun. 2014, 21, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Andrews, J.; Buzzi, S.; Choi, W.; Hanly, S.; Lozano, A.; Soong, A.; Zhang, J. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, J.; Letaief, K.B. Group sparse beamforming for green cloud-ran. IEEE Trans. Wirel. Commun. 2014, 13, 2809–2823. [Google Scholar]
- Wu, J.; Zhang, Y.; Zukerman, M.; Yung, K.N. Energy-efficient base-stations sleep-mode techniques in green cellular networks: A survey. IEEE Commun. Surv. Tutor. 2015, 17, 803–826. [Google Scholar] [CrossRef]
- Tang, J.; Tay, W.; Quek, T. Cross-layer resource allocation with elastic service scaling in cloud radio access network. IEEE Trans. Wirel. Commun. 2015, 14, 5068–5081. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, L.; Xu, Y.; Wei, X. Computationally efficient energy optimization for cloud radio access networks with csi uncertainty. IEEE Trans. Commun. 2017, 65, 5499–5513. [Google Scholar] [CrossRef]
- Dai, B.; Yu, W. Energy efficiency of downlink transmission strategies for cloud radio access networks. IEEE J. Sel. Areas Commun. 2016, 34, 1037–1050. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wu, J.; Peng, M.; Zhang, P. Queue-aware energy-efficient joint remote radio head activation and beamforming in cloud radio access networks. IEEE Trans. Wirel. Commun. 2016, 15, 3880–3894. [Google Scholar] [CrossRef]
- Wyner, A. The Wire-Tap Channel; Technical Report; Wiley-VCH: Hoboken, NJ, USA, 1975. [Google Scholar]
- Khisti, A.; Wornell, G. Secure transmission with multiple antennas-part I the misome wiretap channel. IEEE Trans. Inf. Theory 2010, 56, 3088–3104. [Google Scholar] [CrossRef] [Green Version]
- Khisti, A.; Wornell, G. Secure transmission with multiple antennas-part II the mimome wiretap channel. IEEE Trans. Inf. Theory 2010, 56, 5515–5532. [Google Scholar] [CrossRef] [Green Version]
- Goel, S.; Negi, R. Guaranteeing secrecy using artificial noise. IEEE Trans. Wirel. Commun. 2008, 7, 2180–2189. [Google Scholar] [CrossRef]
- Cumanan, K.; Ding, Z.; Sharif, B.; Tian, G.; Leung, K. Secrecy rate optimizations for a mimo secrecy channel with a multiple-antenna eavesdropper. IEEE Trans. Veh. Technol. 2014, 63, 1678–1690. [Google Scholar] [CrossRef]
- Ng, D.; Lo, E.; Schober, R. Robust beamforming for secure communication in systems with wireless information and power transfer. IEEE Trans. Wirel. Comm. 2014, 13, 4599–4615. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wang, C.; Ng, D.; Lee, M.; Xiao, J. Artificial noise assisted secure transmission for distributed antenna systems. IEEE Trans. Signal Process. 2016, 64, 4050–4064. [Google Scholar] [CrossRef]
- Love, D.; Heath, R., Jr.; Lau, V.; Gesbert, D.; Rao, B.; Andrews, M. An overview of limited feedback in wireless communication systems. IEEE J. Sel. Areas Commun. 2008, 26, 1341–1365. [Google Scholar] [CrossRef]
- Wang, J.; Bengtsson, M.; Ottersten, B.; Palomar, D. Robust MIMO precoding for several classes of channel uncertainty. IEEE Trans. Signal Process. 2013, 61, 3056–3070. [Google Scholar] [CrossRef]
- Shen, C.; Chang, T.; Wang, K.; Qiu, Z.; Chi, C. Distributed robust multicell coordinated beamforming with imperfect CSI: An admm approach. IEEE Trans. Signal Process. 2012, 60, 2988–3003. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Li, Z.; Cheng, J.; Li, Q.; Si, J. Robust AN-aided beamforming and power splitting design for secure MISO cognitive radio with SWIPT. IEEE Trans. Wirel. Commun. 2017, 16, 2450–2464. [Google Scholar] [CrossRef] [Green Version]
- Stephen, B.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; p. 655. [Google Scholar]
- Luo, S.; Zhang, R.; Lim, T. Downlink and uplink energy minimization through user association and beamforming in cloud ran. IEEE Trans. Wirel. Commun. 2015, 14, 494–508. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Gao, Y.; Hanzo, L. Enhancing the physical layer security of non-orthogonal multiple access in large-scale networks. IEEE Trans. Wirel. Commun. 2017, 16, 1656–1672. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, L.; Elkashlan, M.; Nallanathan, A.; Mallik, R.K. Physical layer security in three-tier wireless sensor networks: A stochastic geometry approach. IEEE Trans. Inf. Forensic Secur. 2016, 11, 1128–1138. [Google Scholar] [CrossRef] [Green Version]
- Ng, D.; Schober, R. Secure and green SWIPT in distributed antenna networks with limited backhaul capacity. IEEE Trans. Wirel. Commun. 2015, 14, 5082–5097. [Google Scholar] [CrossRef] [Green Version]
- Shojaeifard, A.; Wong, K.K.; Yu, W.; Zheng, G.; Tang, J. Full-Duplex Cloud Radio Access Network: Stochastic Design and Analysis. IEEE Trans. Wirel. Commun. 2018, 17, 7190–7207. [Google Scholar] [CrossRef]
- Auer, G.; Giannini, V.; Desset, C.; Godor, I.; Skillermark, P.; Olsson, M.; Imran, M.A.; Sabella, D.; Gonzalez, M.J.; Blume, O.; et al. How much energy is needed to run a wireless network? IEEE Wirel. Commun. 2011, 18, 40–49. [Google Scholar] [CrossRef]
- Dhaini, A.; Ho, P.; Shen, G.; Shihada, B. Energy efficiency in tdma-based next-generation passive optical access networks. IEEE/ACM Trans. Netw. 2014, 22, 850–863. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-H.; Simeone, O.; Shamai, S. Fronthaul quantization as artificial noise for enhanced secret communication in C-RAN. In Proceedings of the IEEE International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017. [Google Scholar]
- Rinaldi, F.; Schoen, F.; Sciandrone, M. Concave programming for minimizing the zero-norm over polyhedral sets. Comput. Optim. Appl. 2010, 46, 467–486. [Google Scholar] [CrossRef]
- Tao, M.; Chen, E.; Zhou, H.; Yu, W. Content-centric sparse multicast beamforming for cache-enabled cloud RAN. IEEE Trans. Wirel. Commun. 2016, 15, 6118–6131. [Google Scholar] [CrossRef] [Green Version]
- Marks, B.; Wright, G. A general inner approximation algorithm for nonconvex mathematical programs. Oper. Res. 1978, 26, 681–683. [Google Scholar] [CrossRef]
- Bomze, I.; Lemaréchal, C. Necessary conditions for local optimality in difference-of-convex programming. J. Convex Anal. 2010, 17, 673–680. [Google Scholar]
- Yuille, A.; Rangarajan, A. The concave-convex procedure. Neural Comput. 2003, 15, 915–936. [Google Scholar] [CrossRef]
- Smola, A.; Vishwanathan, S.; Hofmann, T. Kernel methods for missing variables. In Proceedings of the International Workshop Artificial Intelligence and Statistics, Bridgetown, Barbados, 6–8 January 2005; pp. 325–332. [Google Scholar]
- Lipp, T.; Boyd, S. Variations and extension of the convex-concave procedure. Optim. Eng. 2016, 17, 263–287. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0 Beta. 2012. Available online: http://cvxr.com/cvx (accessed on 13 February 2020).
- Luo, Z.; Ma, E.; Thus, M.; Ye, Y.; Zhang, S. Semidefinite relaxation of quadratic optimization problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Pólik, I.; Terlaky, T. Interior point methods for nonlinear optimization. In Nonlinear Optimization; Springer: Berlin/Heidelberger, Germany, 2010; Volume 4, pp. 45–47. [Google Scholar]
- LTE. Evolved Universal Terrestrial Radio Access (E-UTRA); Radio Frequency (RF) Requirements for LTE Pico Node B (Release 9), 3rd Generation Partnership Project (3GPP), TS 36.931, Version 9.0.0; Technical Report; 3GPP: Valbonne, France, 2011. [Google Scholar]






| Sym | Description | Sym | Description |
|---|---|---|---|
| trace of a matrix | expectation operator | ||
| uncertainty channel shape of the ellipsoid of IR k | set of complex numbers | ||
| uncertainty channel shape of the ellipsoid of ER m | transpose | ||
| set of uncertainty channel region of IR k | conjugate transpose | ||
| set of uncertainty channel region of ER m | identity matrix | ||
| complex gaussian distribution | zero matrix | ||
| hardware power consumption of BS l in the active mode | Hermite matrix | ||
| power consumption of BS l in the sleep mode | BS set | ||
| saved power by switching BS l in the sleep mode | active BS set | ||
| constant power consumption of OLT | inactive BS set | ||
| power consumption of ONU l in the active mode | set of exclude | ||
| power consumption of ONU l in the sleep mode | -norm | ||
| both BS l and its corresponding fronthaul link in active mode | -norm | ||
| both BS l and its corresponding fronthaul link in sleep mode | -norm | ||
| mode operator |
| Ch | BS 1 | BS 2 | BS 3 | BS 4 | BS 5 | BS 6 | BS 7 |
|---|---|---|---|---|---|---|---|
| Ch 1 | 0.19 | 0.09 | 0.07 | 0.07 | 0.13 | 1.59 | 0.23 |
| Ch 2 | 8.58 | 2.22 | 3.19 | 1.02 | 2.76 | 12.32 | 2.18 |
| Ch 3 | 4.09 | 2.55 | 2.76 | 4.85 | 12.56 | 7.71 | 1.16 |
| Ch 4 | 2.08 | 0.70 | 1.68 | 3.44 | 2.63 | 1.58 | 2.64 |
| Ch 5 | 4.39 | 12.68 | 2.19 | 0.37 | 1.67 | 2.18 | 14.49 |
| Ch 6 | 7.99 | 1.52 | 6.88 | 7.93 | 1.01 | 1.13 | 0.52 |
| Ch 7 | 4.14 | 5.79 | 1.99 | 0.09 | 2.57 | 3.64 | 0.86 |
| Ch 8 | 1.50 | 10.27 | 3.68 | 0.22 | 2.99 | 0.44 | 2.70 |
| Algorithms | A | (Watt) | (Watt) |
|---|---|---|---|
| Proposed algorithm | 3 | 15.56 | 0.14 |
| -norm algorithm | 4 | 20.28 | 0.07 |
| ExSearch algorithm | 3 | 15.56 | 0.14 |
| Baseline algorithm | 7 | 35.13 | 0.03 |
| Algorithms | ||||
|---|---|---|---|---|
| AN (Watt) | 0.160 | 0.053 | 0.004 | 0.001 |
| DTP (Watt) | 0.317 | 0.134 | 0.013 | 0.008 |
| NP (Watt) | 27.43 | 18.18 | 15.32 | 12.79 |
| AN/DTP(%) | 50.50 | 39.55 | 30.77 | 12.50 |
| 0 | 0.001 | 0.01 | 0.05 | 0.1 | 0.12 | |
|---|---|---|---|---|---|---|
| AN + DTP | 0.149 | 0.409 | 0.545 | 1.028 | 1.443 | 1.767 |
| NP | 15.599 | 17.553 | 18.191 | 18.998 | 19.971 | 20.929 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, R. Robust Power Optimization for Downlink Cloud Radio Access Networks with Physical Layer Security. Entropy 2020, 22, 223. https://doi.org/10.3390/e22020223
Zhang Y, Liu R. Robust Power Optimization for Downlink Cloud Radio Access Networks with Physical Layer Security. Entropy. 2020; 22(2):223. https://doi.org/10.3390/e22020223
Chicago/Turabian StyleZhang, Yijia, and Ruiying Liu. 2020. "Robust Power Optimization for Downlink Cloud Radio Access Networks with Physical Layer Security" Entropy 22, no. 2: 223. https://doi.org/10.3390/e22020223
APA StyleZhang, Y., & Liu, R. (2020). Robust Power Optimization for Downlink Cloud Radio Access Networks with Physical Layer Security. Entropy, 22(2), 223. https://doi.org/10.3390/e22020223




