Thermomass Theory in the Framework of GENERIC
Abstract
:1. Introduction
2. Thermomass Theory
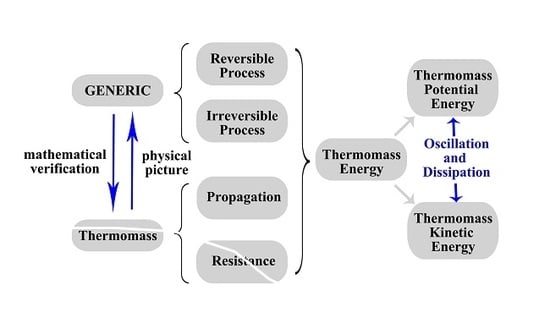
3. Thermomass Theory in the Framework of GENERIC
4. Discussion and Extensions
4.1. Comparisons Between GENERIC Theory and Thermomass Theory
4.2. Thermomass Energy
4.3. Extension in the Framework of GENERIC
5. Numerical Results
5.1. Influences of the Convective Term
5.2. Influences of the Distortion Matrix
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Letters | Greek symbols | ||
| A | function of state variables | β | coefficient (K2/(J·m3)) |
| a | label vector (m) | γ | coefficient (m3·s/kg) |
| CV | specific heat (J/(kg·K)) | ε | coefficient (J·m3/kg2) |
| D | distortion matrix (1) | η | eta-function (J/K) |
| E | energy (J) | κ | coefficient (J·s2·K2/(m11)) |
| e | energy density (J/m3) | π | pressure potential (N/m2) |
| f | resistance force (N/m3) | ρ | density (kg/m3) |
| H | Hamiltonian energy (J/m3) | τ | relaxation time (s) |
| k | thermal conductivity (W/(m·K)) | μ | coefficient (N·s/m4) |
| V | Volume (m3) | φ | coefficient (J/K) |
| L | Poisson bivector | Ξ | dissipation potential (J/m3) |
| M | mass (kg) | χ | coefficient (J/m3) |
| p | thermomass momentum (kg/(m2s) | subscripts | |
| n | state variable | 1,2,3 | orders |
| P | pressure (N/m2) | i,j | component of tensor |
| Q | heat source (W/m3) | h | thermomass |
| s | thermomass source (kg/(m3·s) | k | kinetic energy |
| T | temperature (K) | p | potential energy |
| t | time (s) | c | convective effect |
| x | spatial coordinate (m) | D | distortion effect |
| u | velocity (m/s) | a | label field |
| Y | amplitude (W/m2) | ||
Appendix A. Details of the Numerical Simulations


| Grid Size | 100 × 100 | 150 × 150 | 200 × 200 | 300 × 300 |
|---|---|---|---|---|
| Deviation Percent | 1.07% | 0.3% | — | <0.01% |
| Time Step | 1 × 10−4 | 5 × 10−5 | 2 × 10−5 | 1 × 10−5 | 5 × 10−6 |
|---|---|---|---|---|---|
| Deviation Percent | 0.24% | 0.1% | 0.02% | — | <0.01% |
References
- Ackerman, C.C.; Bertman, B.; Fairbank, H.A.; Guyer, R.A. Second Sound in Solid Helium. Phys. Rev. Lett. 1966, 16, 789–791. [Google Scholar] [CrossRef]
- McNelly, T.F.; Rogers, S.J.; Channin, D.J.; Rollefson, R.J.; Goubau, W.M.; Schmidt, G.E.; Krumhansl, J.A.; Pohl, R.O. Heat pulses in NaF: Onset of second sound. Phys. Rev. Lett. 1970, 24, 100. [Google Scholar] [CrossRef]
- Jackson, H.E.; Walker, C.T.; McNelly, T.F. Second sound in NaF. Phys. Rev. Lett. 1970, 25, 26. [Google Scholar] [CrossRef]
- Narayanamurti, V.; Dynes, R. Observation of second sound in bismuth. Phys. Rev. Lett. 1972, 28, 1461. [Google Scholar] [CrossRef]
- Pohl, D.W.; Irniger, V. Observation of Second Sound in NaF by Means of Light Scattering. Phys. Rev. Lett. 1976, 36, 480–483. [Google Scholar] [CrossRef]
- Huberman, S.; Duncan, R.A.; Chen, K.; Song, B.; Chiloyan, V.; Ding, Z.; Maznev, A.A.; Chen, G.; Nelson, K.A. Observation of second sound in graphite at temperatures above 100 K. Science 2019, 364, 375–379. [Google Scholar] [CrossRef] [Green Version]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Highland, M.; Gundrum, B.C.; Koh, Y.K.; Averback, R.S.; Cahill, D.G.; Elarde, V.C.; Coleman, J.J.; Walko, D.A.; Landahl, E.C. Ballistic-phonon heat conduction at the nanoscale as revealed by time-resolved X-ray diffraction and time-domain thermoreflectance. Phys. Rev. B 2007, 76, 075337. [Google Scholar] [CrossRef]
- Siemens, M.E.; Li, Q.; Yang, R.; Nelson, K.A.; Anderson, E.H.; Murnane, M.M.; Kapteyn, H.C. Quasi-ballistic thermal transport from nanoscale interfaces observed using ultrafast coherent soft X-ray beams. Nat. Mater. 2010, 9, 26–30. [Google Scholar] [CrossRef] [Green Version]
- Hochbaum, A.I.; Chen, R.; Delgado, R.D.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef]
- Hua, Y.C.; Cao, B.Y. Slip Boundary Conditions in Ballistic–Diffusive Heat Transport in Nanostructures. Nanoscale Microscale Thermophys. Eng. 2017, 21, 159–176. [Google Scholar] [CrossRef]
- Hua, Y.C.; Cao, B.Y. Anisotropic Heat Conduction in Two-Dimensional Periodic Silicon Nanoporous Films. J. Phys. Chem. C 2017, 121, 5293–5301. [Google Scholar] [CrossRef]
- Mingo, N.; Broido, D. Length dependence of carbon nanotube thermal conductivity and the “problem of long waves”. Nano lett. 2005, 5, 1221–1225. [Google Scholar] [CrossRef] [PubMed]
- Hyun Oh, J.; Shin, M.; Jang, M.G. Phonon thermal conductivity in silicon nanowires: The effects of surface roughness at low temperatures. J. Appl. Phys. 2012, 111, 044304. [Google Scholar] [CrossRef]
- Straughan, B. Heat Waves; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Tang, D.S.; Hua, Y.C.; Cao, B.Y. Thermal wave propagation through nanofilms in ballistic-diffusive regime by Monte Carlo simulations. Int. J. Therm. Sci. 2016, 109, 81–89. [Google Scholar] [CrossRef]
- Tang, D.S.; Cao, B.Y. Ballistic thermal wave propagation along nanowires modeled using phonon Monte Carlo simulations. Appl. Therm. Eng. 2017, 117, 609–616. [Google Scholar] [CrossRef]
- Hong, B.S.; Su, P.-J.; Chou, C.-Y.; Hung, C.-I. Realization of non-Fourier phenomena in heat transfer with 2D transfer function. Appl. Math. Model. 2011, 35, 4031–4043. [Google Scholar] [CrossRef]
- Hong, B.S.; Chou, C.Y. Realization of Thermal Inertia in Frequency Domain. Entropy 2014, 16, 1101–1121. [Google Scholar] [CrossRef] [Green Version]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Vernotte, P. Paradoxes in the continuous theory of the heat equation. CR Acad. Sci. 1958, 246, 154–155. [Google Scholar]
- Hu, R.; Cao, B. Study on thermal wave based on the thermal mass theory. Sci. China Ser. E Technol. Sci. 2009, 52, 1786–1792. [Google Scholar] [CrossRef]
- Tzou, D.Y. The generalized lagging response in small-scale and high-rate heating. Int. J. Heat Mass Transf. 1995, 38, 3231–3240. [Google Scholar] [CrossRef]
- Tzou, D.Y. Experimental support for the lagging behavior in heat propagation. J. Thermophys. Heat Transf. 1995, 9, 686–693. [Google Scholar] [CrossRef]
- Shen, B.; Zhang, P. Notable physical anomalies manifested in non-Fourier heat conduction under the dual-phase-lag model. Int. J. Heat Mass Transf. 2008, 51, 1713–1727. [Google Scholar] [CrossRef]
- Rukolaine, S.A. Unphysical effects of the dual-phase-lag model of heat conduction. Int. J. Heat Mass Transfer 2014, 78, 58–63. [Google Scholar] [CrossRef]
- Rukolaine, S.A. Unphysical effects of the dual-phase-lag model of heat conduction: Higher-order approximations. Int. J. Therm. Sci. 2017, 113, 83–88. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Solution of the Linearized Phonon Boltzmann Equation. Phys. Rev. 1966, 148, 766–778. [Google Scholar] [CrossRef]
- Guyer, R.A.; Krumhansl, J.A. Thermal Conductivity, Second Sound, and Phonon Hydrodynamic Phenomena in Nonmetallic Crystals. Phys. Rev. 1966, 148, 778–788. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, M. Phonon hydrodynamics and its applications in nanoscale heat transport. Phys. Rep. 2015, 595, 1–44. [Google Scholar] [CrossRef]
- Zhukovsky, K. Violation of the maximum principle and negative solutions for pulse propagation in Guyer–Krumhansl model. Int. J. Heat Mass Transf. 2016, 98, 523–529. [Google Scholar] [CrossRef]
- Zhukovsky, K.V. Exact solution of Guyer–Krumhansl type heat equation by operational method. Int. J. Heat Mass Transf. 2016, 96, 132–144. [Google Scholar] [CrossRef]
- Cao, B.Y.; Guo, Z.Y. Equation of motion of a phonon gas and non-Fourier heat conduction. J. Appl. Phys. 2007, 102, 053503. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Hou, Q.W. Thermal wave based on the thermomass model. J. Heat Transf. 2010, 132, 072403. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, B.Y.; Guo, Z.Y. Generalized heat conduction laws based on thermomass theory and phonon hydrodynamics. J. Appl. Phys. 2011, 110, 063504. [Google Scholar]
- Guo, Z.Y. Energy-Mass Duality of Heat and Its Applications. ES Energy Environ. 2018, 1, 4–15. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, B.Y.; Guo, Z.Y. General expression for entropy production in transport processes based on the thermomass model. Phys. Rev. E 2012, 85, 061107. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Guo, Z.Y. Entropy analyses for hyperbolic heat conduction based on the thermomass model. Int. J. Heat Mass Transf. 2011, 54, 1924–1929. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, B.Y.; Guo, Z.Y. Size dependent thermal conductivity of Si nanosystems based on phonon gas dynamics. Physica E 2014, 56, 256–262. [Google Scholar] [CrossRef]
- Müller, I.; Weiss, W. Thermodynamics of irreversible processes—Past and present. Eur. Phys. J. H 2012, 37, 139–236. [Google Scholar] [CrossRef]
- Grmela, M. Contact Geometry of Mesoscopic Thermodynamics and Dynamics. Entropy 2014, 16, 1652–1686. [Google Scholar] [CrossRef] [Green Version]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended irreversible thermodynamics revisited (1988–98). Rep. Progr. Phys. 1999, 62, 1035. [Google Scholar] [CrossRef]
- Lebon, G.; Casas-Vázquez, J.; Jou, D. Extended irreversible thermodynamics of heat transport. A brief introduction. Proc. Est. Acad. Sci. 2008, 57, 3. [Google Scholar]
- Ván, P. Weakly nonlocal irreversible thermodynamics—The Guyer–Krumhansl and the Cahn–Hilliard equations. Phys. Lett. A 2001, 290, 88–92. [Google Scholar] [CrossRef] [Green Version]
- Ván, P. Weakly nonlocal irreversible thermodynamics. Ann. Phys. 2003, 12, 146–173. [Google Scholar] [CrossRef] [Green Version]
- Ván, P.; Fülöp, T. Universality in heat conduction theory: Weakly nonlocal thermodynamics. Ann. Phys. 2012, 524, 470–478. [Google Scholar] [CrossRef] [Green Version]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Zhu, Y.; Hong, L.; Yang, Z.; Yong, W.-A. Conservation-dissipation formalism of irreversible thermodynamics. J. Non-Equilib. Thermodyn. 2015, 40, 67–74. [Google Scholar] [CrossRef] [Green Version]
- Öttinger, H.C.; Grmela, M. Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism. Phys. Rev. E 1997, 56, 6633. [Google Scholar]
- Grmela, M.; Hong, L.; Jou, D.; Lebon, G.; Pavelka, M. Hamiltonian and Godunov structures of the Grad hierarchy. Phys. Rev. E 2017, 95, 033121. [Google Scholar] [CrossRef] [Green Version]
- Peshkov, I.; Pavelka, M.; Romenski, E.; Grmela, M. Continuum Mechanics and Thermodynamics in the Hamilton and the Godunov-type Formulations. Continuum Mech. Thermodyn. 2017, 30, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620. [Google Scholar] [CrossRef]
- Hoyuelos, M. GENERIC framework for the Fokker–Planck equation. Physica A 2016, 442, 350–358. [Google Scholar] [CrossRef]
- Grmela, M.; Lebon, G.; Dubois, C. Multiscale thermodynamics and mechanics of heat. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2011, 83, 061134. [Google Scholar] [CrossRef] [PubMed]
- Grmela, M.; Teichmann, J. Lagrangian formulation of the Maxwell-Cattaneo hydrodynamics. Int. J. Eng. Sci. 1983, 21, 297–313. [Google Scholar] [CrossRef]
- Grmela, M. A framework for elasto-plastic hydrodynamics. Phys. Lett. A 2003, 312, 136–146. [Google Scholar] [CrossRef]
- Maldovan, M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D. A Course in Computational Fluid Dynamics; Higher Education Press: Beijing, China, 2010; pp. 185–189. [Google Scholar]
- Zhang, M.K.; Cao, B.Y.; Guo, Y.C. Numerical studies on damping of thermal waves. Int. J. Therm. Sci. 2014, 84, 9–20. [Google Scholar] [CrossRef]
- Zhang, M.K.; Cao, B.Y.; Guo, Y.C. Numerical studies on dispersion of thermal waves. Int. J. Heat Mass Transf. 2013, 67, 1072–1082. [Google Scholar] [CrossRef]
- Nie, B.D.; Cao, B.Y. Reflection and refraction of a thermal wave at an ideal interface. Int. J. Heat Mass Transf. 2018, 116, 314–328. [Google Scholar] [CrossRef]
- Nie, B.D.; Cao, B.Y. Three mathematical representations and an improved ADI method for hyperbolic heat conduction. Int. J. Heat Mass Transf. 2019, 135, 974–984. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, B.-D.; Cao, B.-Y.; Guo, Z.-Y.; Hua, Y.-C. Thermomass Theory in the Framework of GENERIC. Entropy 2020, 22, 227. https://doi.org/10.3390/e22020227
Nie B-D, Cao B-Y, Guo Z-Y, Hua Y-C. Thermomass Theory in the Framework of GENERIC. Entropy. 2020; 22(2):227. https://doi.org/10.3390/e22020227
Chicago/Turabian StyleNie, Ben-Dian, Bing-Yang Cao, Zeng-Yuan Guo, and Yu-Chao Hua. 2020. "Thermomass Theory in the Framework of GENERIC" Entropy 22, no. 2: 227. https://doi.org/10.3390/e22020227