Detrending the Waveforms of Steady-State Vowels
Abstract
Relation of This Work to the Conference Paper
1. Introduction
1.1. Background
1.2. The Pinson Model
1.3. The Proposed Model for a Single Pitch Period
1.4. Outline
2. A Pitch-Synchronous Linear Model for Steady-State Vowels
2.1. The Model Function
2.2. The Priors
2.3. The Likelihood Function
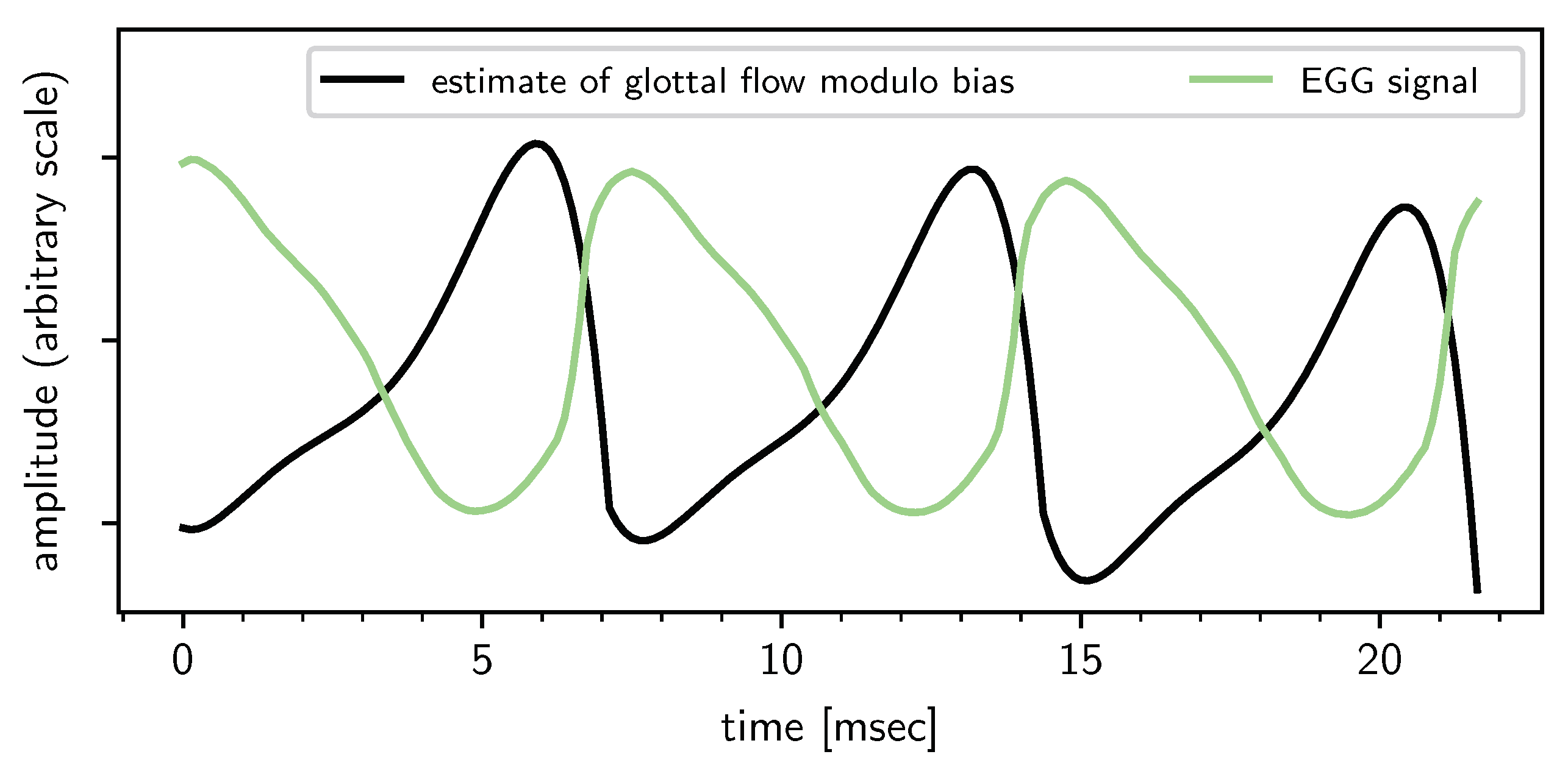
2.4. The Origin of the Trend
3. Inferring the Formant Bandwidths and Frequencies: Theory
3.1. The Integrated Likelihood
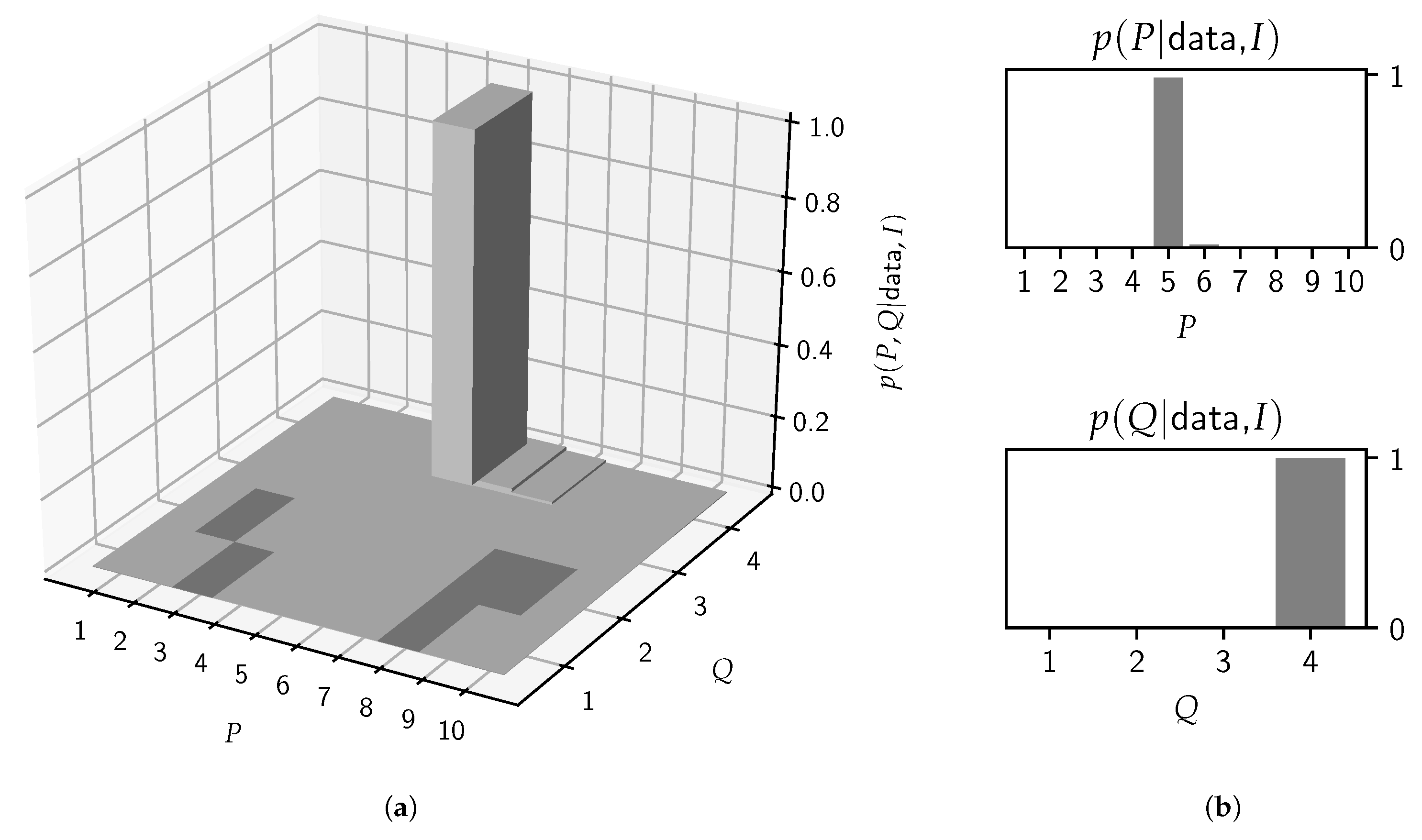
3.2. Optimization Approaches
4. Application to Data
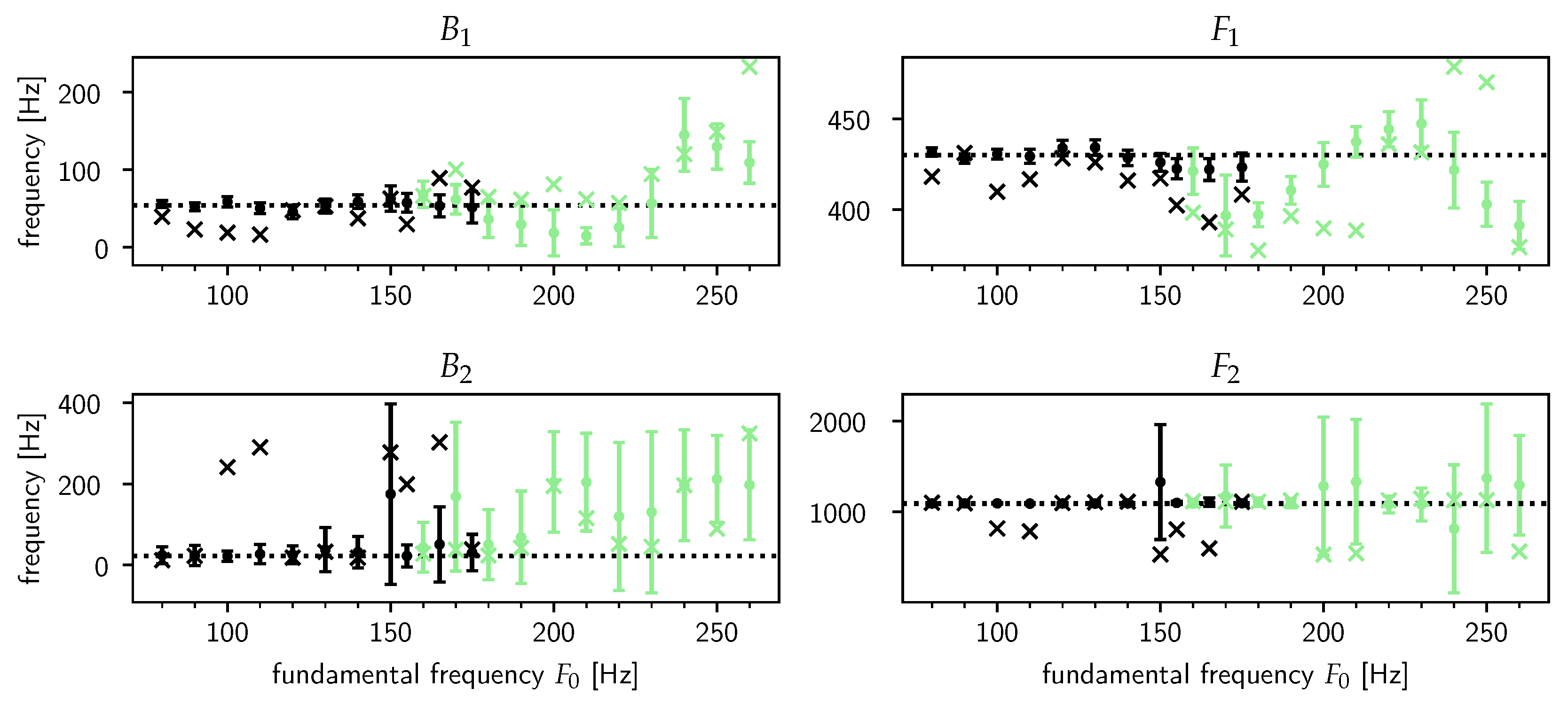
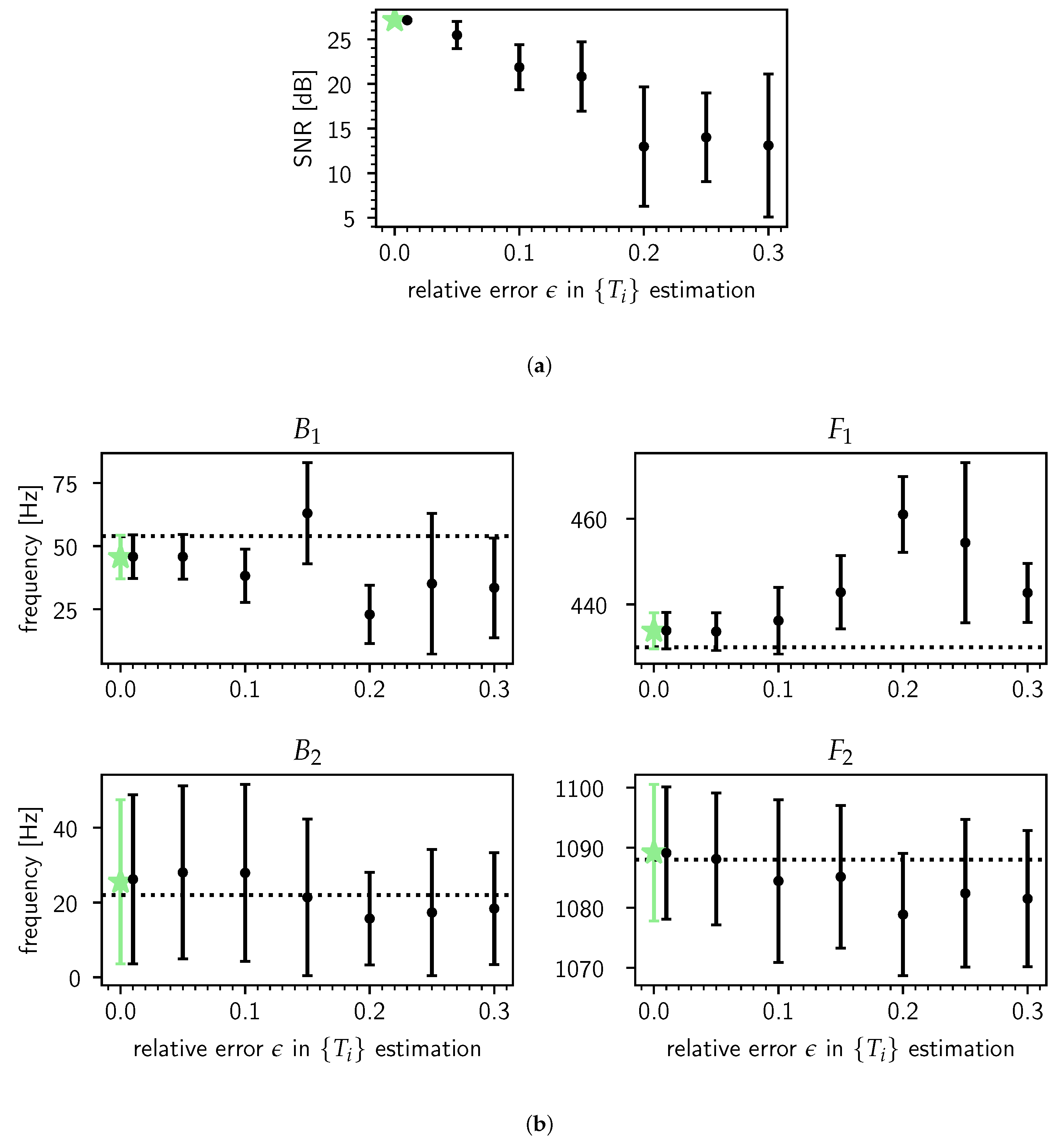
4.1. Synthesized Steady-State /ɤ/
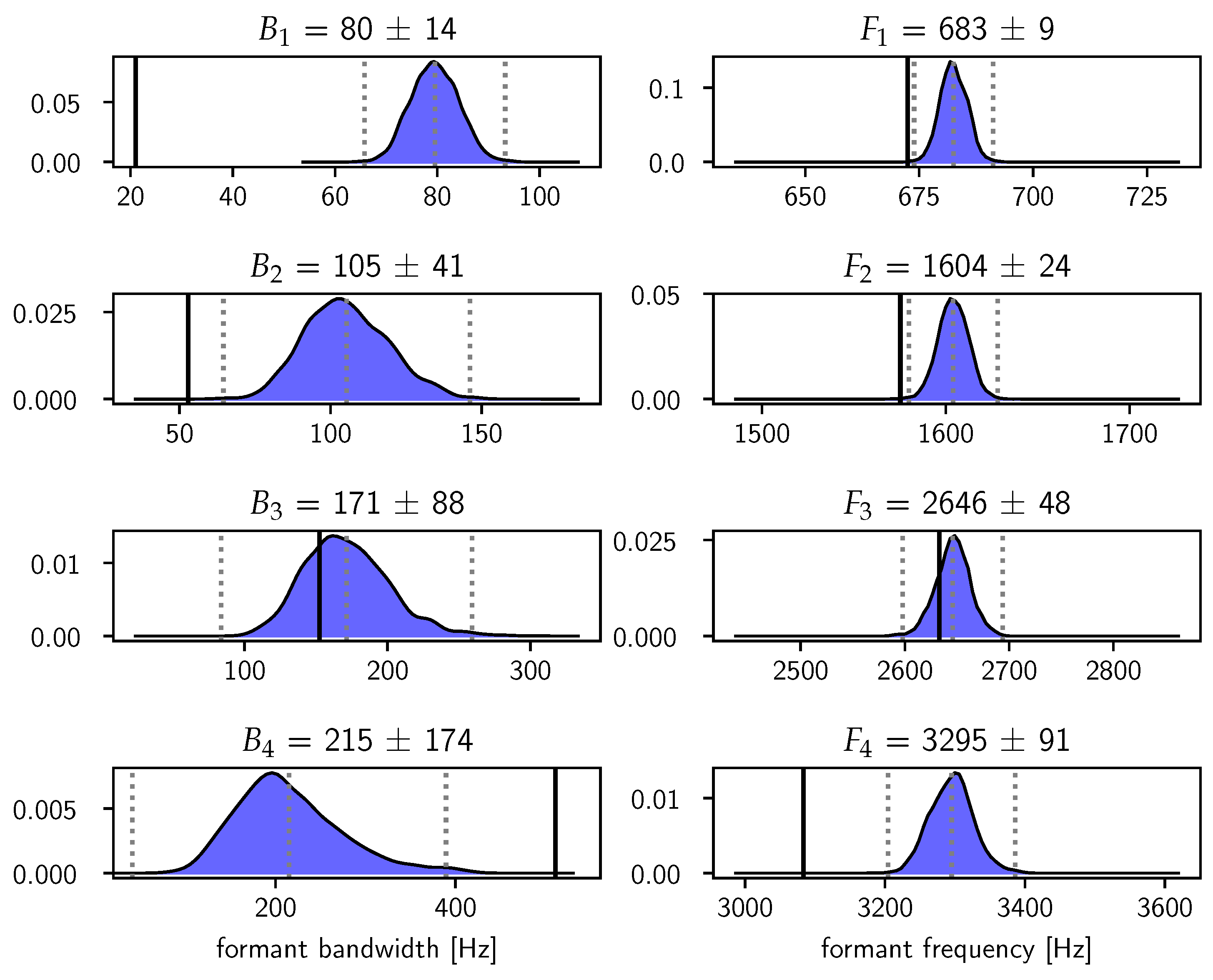
4.2. Real Steady-State /æ/
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Notes
- Van Soom, M.; de Boer, B. A New Approach to the Formant Measuring Problem. Proceedings 2019, 33, 29. [Google Scholar] [CrossRef]
- Fulop, S.A. Speech Spectrum Analysis; OCLC: 746243279; Signals and Communication Technology; Springer: Berlin, Germany, 2011. [Google Scholar]
- Fant, G. Acoustic Theory of Speech Production; Mouton: Den Haag, The Netherlands, 1960. [Google Scholar]
- Stevens, K.N. Acoustic Phonetics; MIT Press: Cambridge, CA, USA, 2000. [Google Scholar]
- Rabiner, L.R.; Schafer, R.W. Introduction to Digital Speech Processing; Foundations and Trends in Signal Processing: Hanover, MA, USA, 2007. [Google Scholar] [CrossRef]
- Rose, P. Forensic Speaker Identification; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Ng, A.K.; Koh, T.S.; Baey, E.; Lee, T.H.; Abeyratne, U.R.; Puvanendran, K. Could Formant Frequencies of Snore Signals Be an Alternative Means for the Diagnosis of Obstructive Sleep Apnea? Sleep Med. 2008, 9, 894–898. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Raj, B.; Gencaga, D. Forensic Anthropometry from Voice: An Articulatory-Phonetic Approach. In Proceedings of the 2016 39th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 30 May–3 June 2016; pp. 1375–1380. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Bretthorst, G.L., Ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2003. [Google Scholar]
- Bonastre, J.F.; Kahn, J.; Rossato, S.; Ajili, M. Forensic Speaker Recognition: Mirages and Reality. Available online: https://www.oapen.org/download?type=document&docid=1002748#page=257 (accessed on 12 March 2020).
- Hughes, N.; Karabiyik, U. Towards reliable digital forensics investigations through measurement science. WIREs Forensic Sci. 2020, e1367. [Google Scholar] [CrossRef]
- De Witte, W. A Forensic Speaker Identification Study: An Auditory-Acoustic Analysis of Phonetic Features and an Exploration of the “Telephone Effect”. Ph.D. Thesis, Universitat Autònoma de Barcelona, Bellaterra, Spain, 2017. [Google Scholar]
- Kent, R.D.; Vorperian, H.K. Static Measurements of Vowel Formant Frequencies and Bandwidths: A Review. J. Commun. Disord. 2018, 74, 74–97. [Google Scholar] [CrossRef]
- Mehta, D.D.; Wolfe, P.J. Statistical Properties of Linear Prediction Analysis Underlying the Challenge of Formant Bandwidth Estimation. J. Acoust. Soc. Am. 2015, 137, 944–950. [Google Scholar] [CrossRef]
- Harrison, P. Making Accurate Formant Measurements: An Empirical Investigation of the Influence of the Measurement Tool, Analysis Settings and Speaker on Formant Measurements. Ph.D. Thesis, University of York, York, UK, 2013. [Google Scholar]
- Maurer, D. Acoustics of the Vowel; Peter Lang: Bern, Switzerland, 2016. [Google Scholar]
- Shadle, C.H.; Nam, H.; Whalen, D.H. Comparing Measurement Errors for Formants in Synthetic and Natural Vowels. J. Acoust. Soc. Am. 2016, 139, 713–727. [Google Scholar] [CrossRef]
- Knuth, K.H.; Skilling, J. Foundations of Inference. Axioms 2012, 1, 38–73. [Google Scholar] [CrossRef]
- Pinson, E.N. Pitch-Synchronous Time-Domain Estimation of Formant Frequencies and Bandwidths. J. Acoust. Soc. Am. 1963, 35, 1264–1273. [Google Scholar] [CrossRef]
- Fitzgerald, W.J.; Niranjan, M. Speech Processing Using Bayesian Inference. In Maximum Entropy and Bayesian Methods: Paris, France, 1992; Mohammad-Djafari, A., Demoment, G., Eds.; Fundamental Theories of Physics; Springer: Dordrecht, The Netherlands, 1993; pp. 215–223. [Google Scholar] [CrossRef]
- Nielsen, J.K.; Christensen, M.G.; Jensen, S.H. Default Bayesian Estimation of the Fundamental Frequency. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 598–610. [Google Scholar] [CrossRef]
- Peterson, G.E.; Shoup, J.E. The Elements of an Acoustic Phonetic Theory. J. Speech Hear. Res. 1966, 9, 68–99. [Google Scholar] [CrossRef] [PubMed]
- Little, M.A.; McSharry, P.E.; Roberts, S.J.; Costello, D.A.; Moroz, I.M. Exploiting Nonlinear Recurrence and Fractal Scaling Properties for Voice Disorder Detection. Biomed. Eng. Online 2007, 6, 23. [Google Scholar] [CrossRef] [PubMed]
- Titze, I.R. Workshop on Acoustic Voice Analysis: Summary Statement; National Center for Voice and Speech: Salt Lake City, UT, USA, 1995. [Google Scholar]
- While our (and others’ [27]) everyday experience of looking at speech waveforms confirms this, we would be very interested in a formal study on this subject.
- Hermann, L. Phonophotographische Untersuchungen. Pflüg. Arch. 1889, 45, 582–592. [Google Scholar] [CrossRef]
- Chen, C.J. Elements of Human Voice; World Scientific: Singapore, 2016. [Google Scholar] [CrossRef]
- Scripture, E.W. The Elements of Experimental Phonetics; C. Scribner’s Sons: New York, NY, USA, 1904. [Google Scholar]
- Kominek, J.; Black, A.W. The CMU Arctic Speech Databases. 2004. Available online: http://festvox.org/cmu_arctic/cmu_arctic_report.pdf (accessed on 12 March 2020).
- Ladefoged, P. Elements of Acoustic Phonetics; University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Drugman, T.; Thomas, M.; Gudnason, J.; Naylor, P.; Dutoit, T. Detection of Glottal Closure Instants From Speech Signals: A Quantitative Review. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 994–1006. [Google Scholar] [CrossRef]
- Fant, G. The LF-model revisited. Transformations and frequency domain analysis. Speech Trans. Lab. Q. Rep. R. Inst. Tech. Stockh. 1995, 2, 40. [Google Scholar]
- Thus, when a vowel is perceived with a clear and constant pitch, it is reasonable to assume that the vowel attained steady-state at some point (though perceptual effects forbid a one-to-one correspondence).
- Fant, G. Formant Bandwidth Data. STL-QPSR 1962, 3, 1–3. [Google Scholar]
- House, A.S.; Stevens, K.N. Estimation of Formant Band Widths from Measurements of Transient Response of the Vocal Tract. J. Speech Hear. Res. 1958, 1, 309–315. [Google Scholar] [CrossRef]
- Sanchez, J. Application of Classical, Bayesian and Maximum Entropy Spectrum Analysis to Nonstationary Time Series Data. In Maximum Entropy and Bayesian Methods; Springer: Berlin/Heidelberger, Germany, 1989; pp. 309–319. [Google Scholar]
- Skilling, J. Nested Sampling for General Bayesian Computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- ÓRuanaidh, J.J.K.; Fitzgerald, W.J. Numerical Bayesian Methods Applied to Signal Processing; Statistics and Computing; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Bretthorst, G.L. Bayesian Spectrum Analysis and Parameter Estimation; Springer Science & Business Media: Berlin/Heidelberger, Germany, 1988. [Google Scholar]
- Jaynes, E.T. Bayesian Spectrum and Chirp Analysis. In Maximum-Entropy and Bayesian Spectral Analysis and Estimation Problems; Reidel: Dordrecht, The Netherlands, 1987; pp. 1–29. [Google Scholar]
- Sivia, D.; Skilling, J. Data Analysis: A Bayesian Tutorial; OUP: Oxford, UK, 2006. [Google Scholar]
- These are improved versions of the ones used in the conference paper.
- This makes no difference in the posterior distribution for θ because the Legendre functions are linear combinations of the polynomials.
- In our experiments, this regularizer prevented a situation that can best be described as polynomial and sinusoidal basis functions with huge amplitudes conspiring together into creating beats that, added together, fitted the data quite well but would yield nonphysical values for the θ.
- Peterson, G.E.; Barney, H.L. Control Methods Used in a Study of the Vowels. J. Acoust. Soc. Am. 1952, 24, 175–184. [Google Scholar] [CrossRef]
- Another approach which avoids setting these prior ranges explicitly uses the perceived reliability of the LPC estimates to assign an expected relative accuracy ρ (e.g., 10%) to the LPC estimates LPC. It is then possible to assign lognormal prior pdfs for the θ which are parametrized by setting the mean and standard deviation of the underlying normal distributions to logLPC and ρ, respectively [41]. This works well as long as ρ ≤ 0.40, regardless of the value of LPC. We use the same technique in Section 4.1 to simulate errors in pitch period segmentation.
- Fant, G. The Voice Source-Acoustic Modeling. STL-QPSR 1982, 4, 28–48. [Google Scholar]
- Rabiner, L.R.; Juang, B.H.; Rutledge, J.C. Fundamentals of Speech Recognition; PTR Prentice Hall Englewood Cliffs: Upper Saddle River, NJ, USA, 1993; Volume 14. [Google Scholar]
- Deller, J.R. On the Time Domain Properties of the Two-Pole Model of the Glottal Waveform and Implications for LPC. Speech Commun. 1983, 2, 57–63. [Google Scholar] [CrossRef]
- Petersen, K.; Pedersen, M. The Matrix Cookbook; Technical University of Denmark: Copenhagen, Denmark, 2008; Volume 7. [Google Scholar]
- Golub, G.; Pereyra, V. Separable nonlinear least squares: The variable projection method and its applications. Inverse Prob. 2003, 19, R1. [Google Scholar] [CrossRef]
- Boersma, P. Praat, a system for doing phonetics by computer. Glot. Int. 2001, 5, 341–345. [Google Scholar]
- Jadoul, Y.; Thompson, B.; de Boer, B. Introducing Parselmouth: A Python interface to Praat. J. Phonetics 2018, 71, 1–15. [Google Scholar] [CrossRef]
- Speagle, J.S. dynesty: A dynamic nested sampling package for estimating Bayesian posteriors and evidences. arXiv 2019, arXiv:1904.02180. [Google Scholar] [CrossRef]
- Vallée, N. Systèmes Vocaliques: De La Typologie Aux Prédictions. Ph.D. Thesis, l’Université Stendhal, Leeuwarden, The Netherlands, 1994. [Google Scholar]
- Fant, G.; Liljencrants, J.; Lin, Q.G. A Four-Parameter Model of Glottal Flow. STL-QPSR 1985, 4, 1–13. [Google Scholar]
- Praat’s default formant estimation algorithm preprocesses the speech data by applying a +6 dB/octave pre-emphasis filter to boost the amplitudes of the higher formants. The goal of this common technique [2] is to facilitate the measurement of the higher formants’ bandwidths and frequencies. We have not applied pre-emphasis in our experiments, so it remains to be seen whether the third formant could have been picked up in this case. On that note, it might be of interest that this plus 6 dB/oct pre-emphasis filter can be expressed in our Bayesian approach as prior covariance matrices {Σi} for the noise vectors {ei} in Equation (5) specifying approximately a minus 6 dB/oct slope for the prior noise spectral density. To see this, write the pre-emphasis operation on the data and model functions as: di → Eidi, Gi→EiGi, (i = 1 ⋯ n), where Ei is a real and invertible Ni × Ni matrix representing the pre-emphasis filter (for example, Praat by default uses yt ≈ xt − 0.98xt−1 which corresponds to Ei having ones on the principal diagonal and −0.98 on the subdiagonal). Then, the likelihood function in Equation (8) is proportional to exp{−(1/2) (di − Gibi)T (di − Gibi)} where the Σi ∝ (Ei)−1 are positive definite covariance matrices specifying the prior for the spectral density of the noise, which turns out to be approximately −6 dB/oct. Thus, pre-emphasis preprocessing can be interpreted as a more informative noise prior.
- Titze, I.R. Principles of Voice Production (Second Printing); National Center for Voice and Speech: Iowa City, IA, USA, 2000. [Google Scholar]
- Sundberg, J. Synthesis of singing. Swed. J. Musicol. 1978, 107–112. [Google Scholar]
- Schroeder, M.R. Computer Speech: Recognition, Compression, Synthesis; Springer Series in Information Sciences; Springer-Verlag: Berlin/Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]



| /ɤ/ | 10 | 180 | 10 | 250 | 10 | 420 | / | 200 | 700 | 700 | 1500 | 1500 | 3000 | / | ||
| /æ/ | 40 | 180 | 40 | 250 | 60 | 420 | 60 | 420 | 300 | 900 | 1000 | 2000 | 2000 | 3000 | 2500 | 4000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Soom, M.; de Boer, B. Detrending the Waveforms of Steady-State Vowels. Entropy 2020, 22, 331. https://doi.org/10.3390/e22030331
Van Soom M, de Boer B. Detrending the Waveforms of Steady-State Vowels. Entropy. 2020; 22(3):331. https://doi.org/10.3390/e22030331
Chicago/Turabian StyleVan Soom, Marnix, and Bart de Boer. 2020. "Detrending the Waveforms of Steady-State Vowels" Entropy 22, no. 3: 331. https://doi.org/10.3390/e22030331
APA StyleVan Soom, M., & de Boer, B. (2020). Detrending the Waveforms of Steady-State Vowels. Entropy, 22(3), 331. https://doi.org/10.3390/e22030331





