Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues
Abstract
:1. Introduction
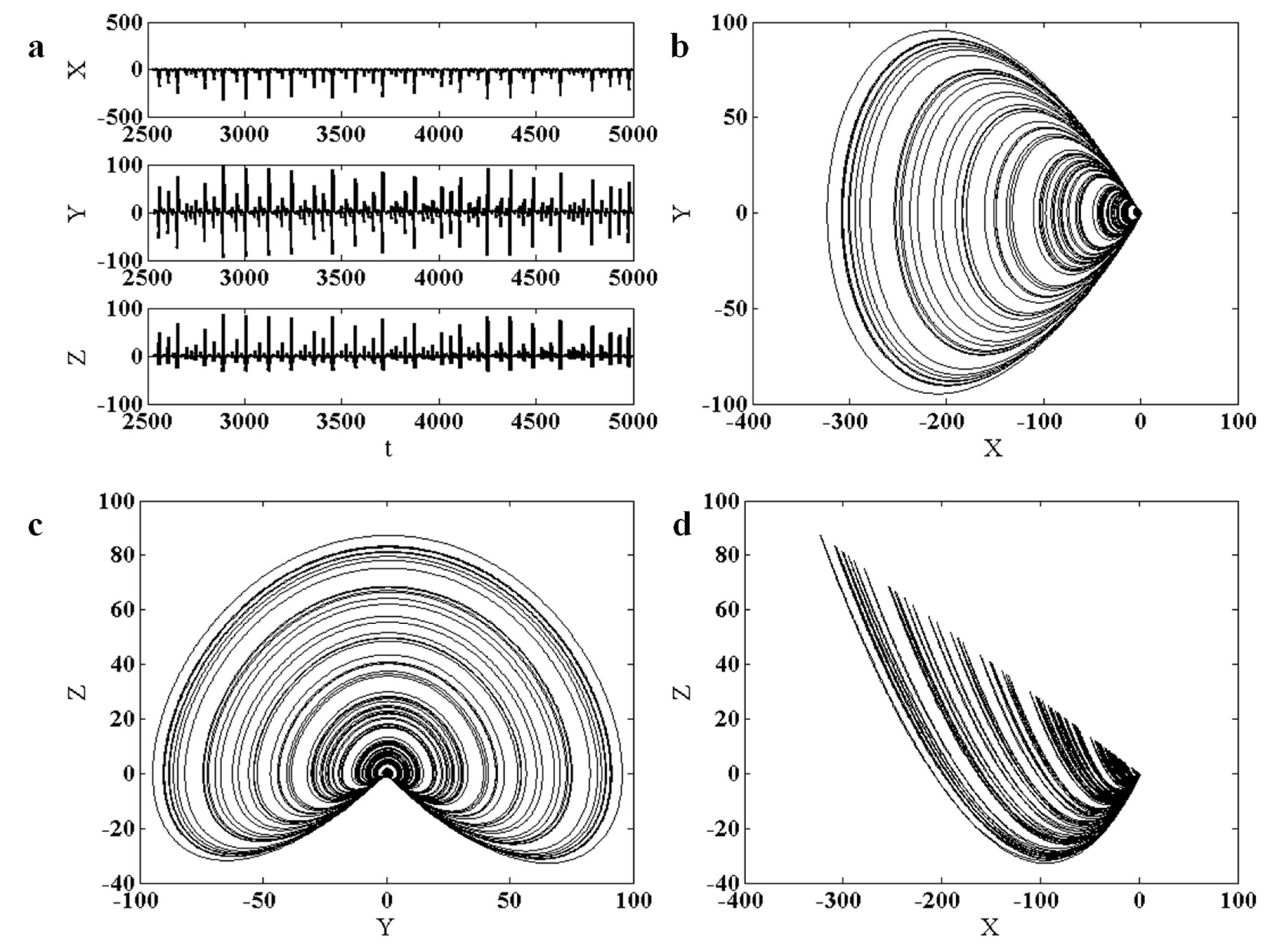
2. The Proposed Chaotic System and Its Properties
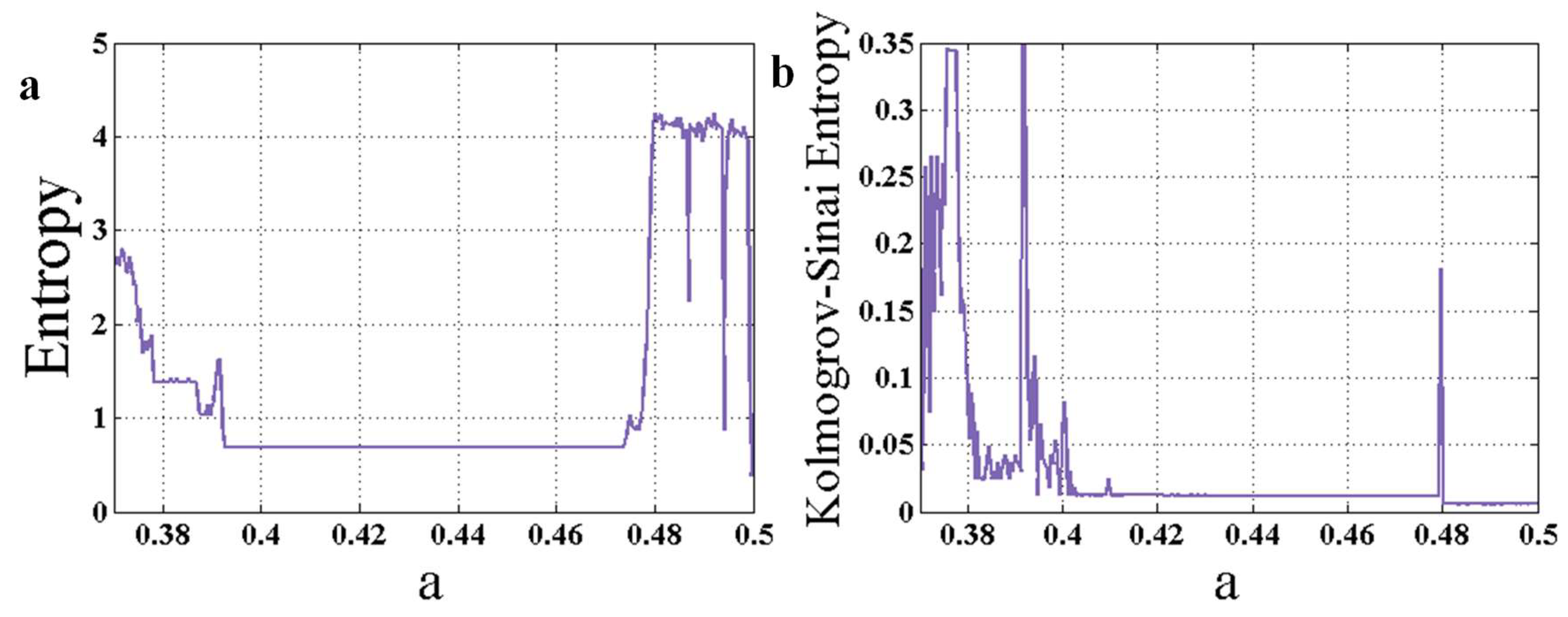
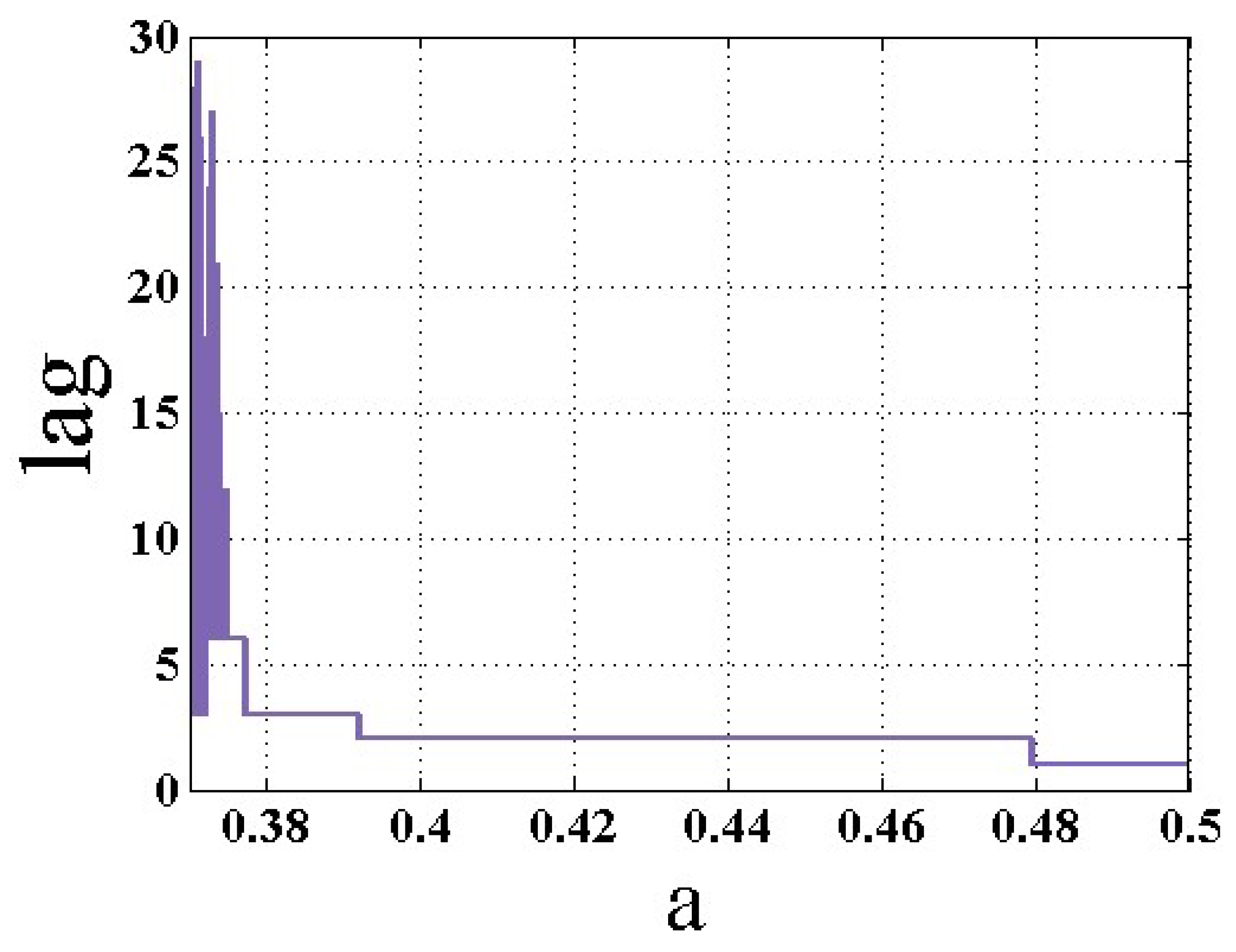
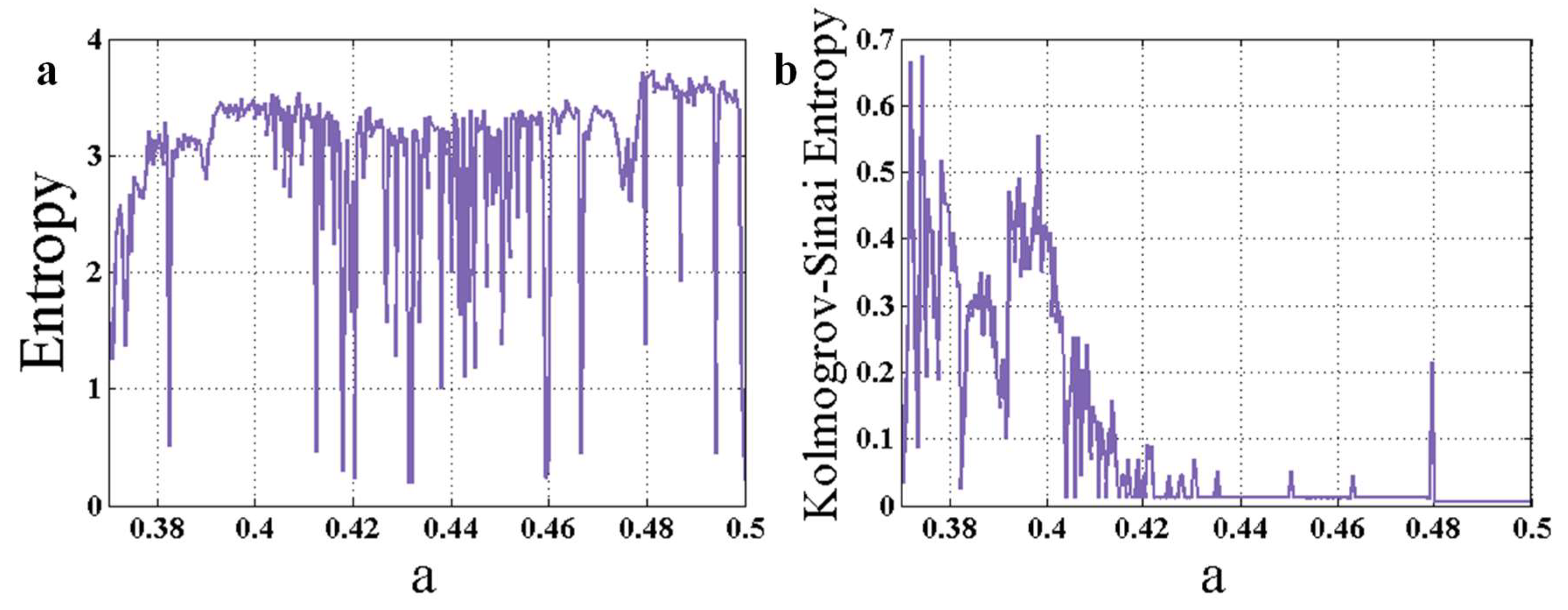
3. Entropy Analysis as an Early Warning Signal
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, H.; Bao, B.; Liu, Z.; Xu, Q.; Jiang, P. Chaotic and periodic bursting phenomena in a memristive Wien-bridge oscillator. Nonlinear Dyn. 2016, 83, 893–903. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef] [Green Version]
- Jafari, S.; Sprott, J.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Ruan, J.; Sun, K.; Mou, J.; He, S.; Zhang, L. Fractional-order simplest memristor-based chaotic circuit with new derivative. Eur. Phys. J. Plus 2018, 133, 3. [Google Scholar] [CrossRef]
- Alamodi, A.O.; Sun, K.; Ai, W.; Chen, C.; Peng, D. Design new chaotic maps based on dimension expansion. Chin. Phys. B 2019, 28, 020503. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Hashemi Golpayegani, S.M.R. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Gotthans, T.; Sprott, J.C.; Petrzela, J. Simple chaotic flow with circle and square equilibrium. Int. J. Bifurc. Chaos 2016, 26, 1650137. [Google Scholar] [CrossRef]
- Ai, W.; Sun, K.; Fu, Y. Design of multiwing-multiscroll grid compound chaotic system and its circuit implementation. Int. J. Mod. Phys. C 2018, 29, 1850049. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Molaie, M. A simple chaotic flow with a plane of equilibria. Int. J. Bifurc. Chaos 2016, 26, 1650098. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Gotthans, T.; Petržela, J. New class of chaotic systems with circular equilibrium. Nonlinear Dyn. 2015, 81, 1143–1149. [Google Scholar] [CrossRef] [Green Version]
- Sambas, A.; Mamat, M.; Arafa, A.A.; Mahmoud, G.M.; Mohamed, M.A.; Sanjaya, W. A new chaotic system with line of equilibria: Dynamics, passive control and circuit design. Int. J. Electr. Comput. Eng. 2019, 9. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud, G.M.; Abed-Elhameed, T.M.; Ahmed, M.E. Generalization of combination–combination synchronization of chaotic n-dimensional fractional-order dynamical systems. Nonlinear Dyn. 2016, 83, 1885–1893. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; He, S.; Wang, H.; Xu, Y. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. Eur. Phys. J. Plus 2017, 132, 31. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Arafa, A.A.; Abed-Elhameed, T.M.; Mahmoud, E.E. Chaos control of integer and fractional orders of chaotic Burke–Shaw system using time delayed feedback control. Chaos Solitons Fractals 2017, 104, 680–692. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Farghaly, A.A.; Abed-Elhameed, T.M.; Aly, S.A.; Arafa, A.A. Dynamics of distributed-order hyperchaotic complex van der Pol oscillators and their synchronization and control. Eur. Phys. J. Plus 2020, 135, 32. [Google Scholar] [CrossRef]
- Dina, Q.; Elabbasyb, E.; Elsadanyc, A.; Ibrahimd, S. Bifurcation analysis and chaos control of a second-order exponential difference equation. Filomat 2019, 33, 5003–5022. [Google Scholar] [CrossRef] [Green Version]
- Din, Q.; Elsadany, A.; Ibrahim, S. Bifurcation analysis and chaos control in a second-order rational difference equation. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 53–68. [Google Scholar] [CrossRef]
- Hilborn, R.C. Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Sprott, J.C. Elegant Chaos: Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Khajanchi, S.; Perc, M.; Ghosh, D. The influence of time delay in a chaotic cancer model. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 103101. [Google Scholar] [CrossRef]
- Ginoux, J.-M.; Ruskeepää, H.; Perc, M.; Naeck, R.; Di Costanzo, V.; Bouchouicha, M.; Fnaiech, F.; Sayadi, M.; Hamdi, T. Is type 1 diabetes a chaotic phenomenon? Chaos Solitons Fractals 2018, 111, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Elsonbaty, A.; Elsadany, A. Bifurcation analysis of chaotic geomagnetic field model. Chaos Solitons Fractals 2017, 103, 325–335. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Jafari, S.; Hashemi Golpayegani, S.M.R.; Perc, M.; Sprott, J.C. Predicting tipping points of dynamical systems during a period-doubling route to chaos. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 073102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Golpayegani, S.M.R.H.; Hatef, B. Does the onset of epileptic seizure start from a bifurcation point? Eur. Phys. J. Spec. Top. 2018, 227, 697–705. [Google Scholar] [CrossRef]
- Dakos, V.; Carpenter, S.R.; Brock, W.A.; Ellison, A.M.; Guttal, V.; Ives, A.R.; Kefi, S.; Livina, V.; Seekell, D.A.; van Nes, E.H. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 2012, 7, 41010. [Google Scholar] [CrossRef] [Green Version]
- Nazarimehr, F.; Ghaffari, A.; Jafari, S.; Golpayegani, S.M.R.H. Sparse Recovery and Dictionary Learning to Identify the Nonlinear Dynamical Systems: One Step Toward Finding Bifurcation Points in Real Systems. Int. J. Bifurc. Chaos 2019, 29, 1950030. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Jafari, S.; Golpayegani, S.M.R.H.; Sprott, J. Can Lyapunov exponent predict critical transitions in biological systems? Nonlinear Dyn. 2017, 88, 1493–1500. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; Van de Koppel, J.; Van de Leemput, I.A.; Levin, S.A.; Van Nes, E.H. Anticipating critical transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef] [Green Version]
- Blahut, R.E.; Blahut, R.E. Principles and Practice of Information Theory; Addison-Wesley: Reading, MA, USA, 1987; Volume 1. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois press: Champaign, IL, USA, 1998. [Google Scholar]
- Baptista, M.; Ngamga, E.; Pinto, P.R.; Brito, M.; Kurths, J. Kolmogorov–Sinai entropy from recurrence times. Phys. Lett. A 2010, 374, 1135–1140. [Google Scholar] [CrossRef] [Green Version]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Nazarimehr, F.; Jafari, S.; Tlelo-Cuautle, E.; Hussain, I. Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues. Entropy 2020, 22, 341. https://doi.org/10.3390/e22030341
Chen L, Nazarimehr F, Jafari S, Tlelo-Cuautle E, Hussain I. Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues. Entropy. 2020; 22(3):341. https://doi.org/10.3390/e22030341
Chicago/Turabian StyleChen, Lianyu, Fahimeh Nazarimehr, Sajad Jafari, Esteban Tlelo-Cuautle, and Iqtadar Hussain. 2020. "Investigation of Early Warning Indexes in a Three-Dimensional Chaotic System with Zero Eigenvalues" Entropy 22, no. 3: 341. https://doi.org/10.3390/e22030341





