Heat Transfer Enhancement in Unsteady MHD Natural Convective Flow of CNTs Oldroyd-B Nanofluid under Ramped Wall Velocity and Ramped Wall Temperature
Abstract
1. Introduction
2. Mathematical Modeling and Formulation of Problem
3. Analytical Solutions
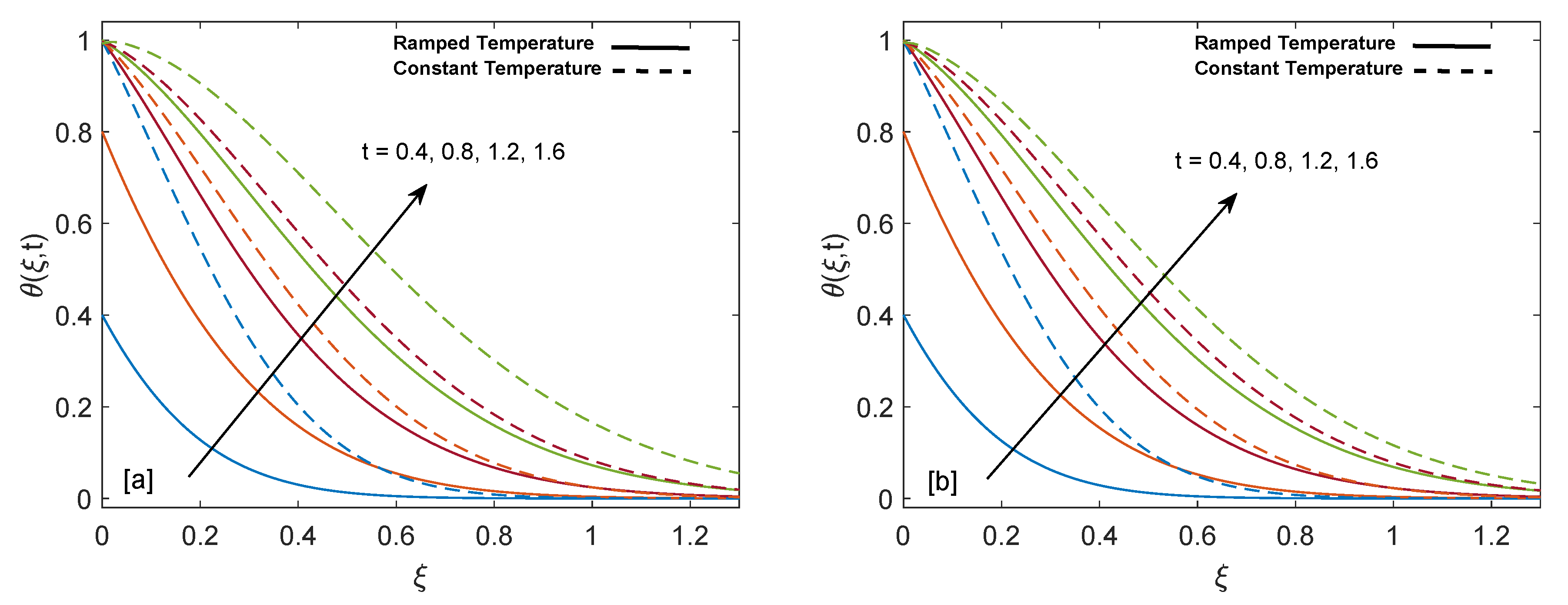
3.1. Temperature Field
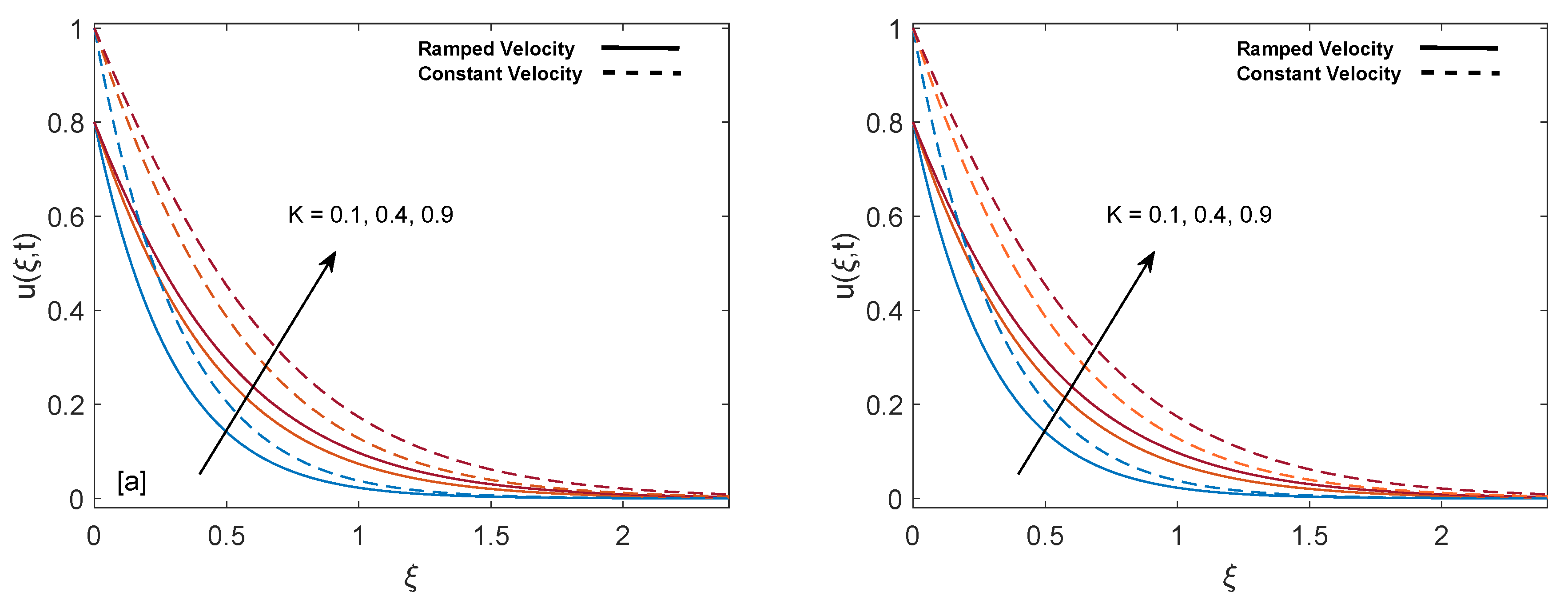
3.2. Velocity Field
3.3. Shear Field
3.4. Nusselt Number
4. Special Cases
4.1. Case 1
4.2. Case 2
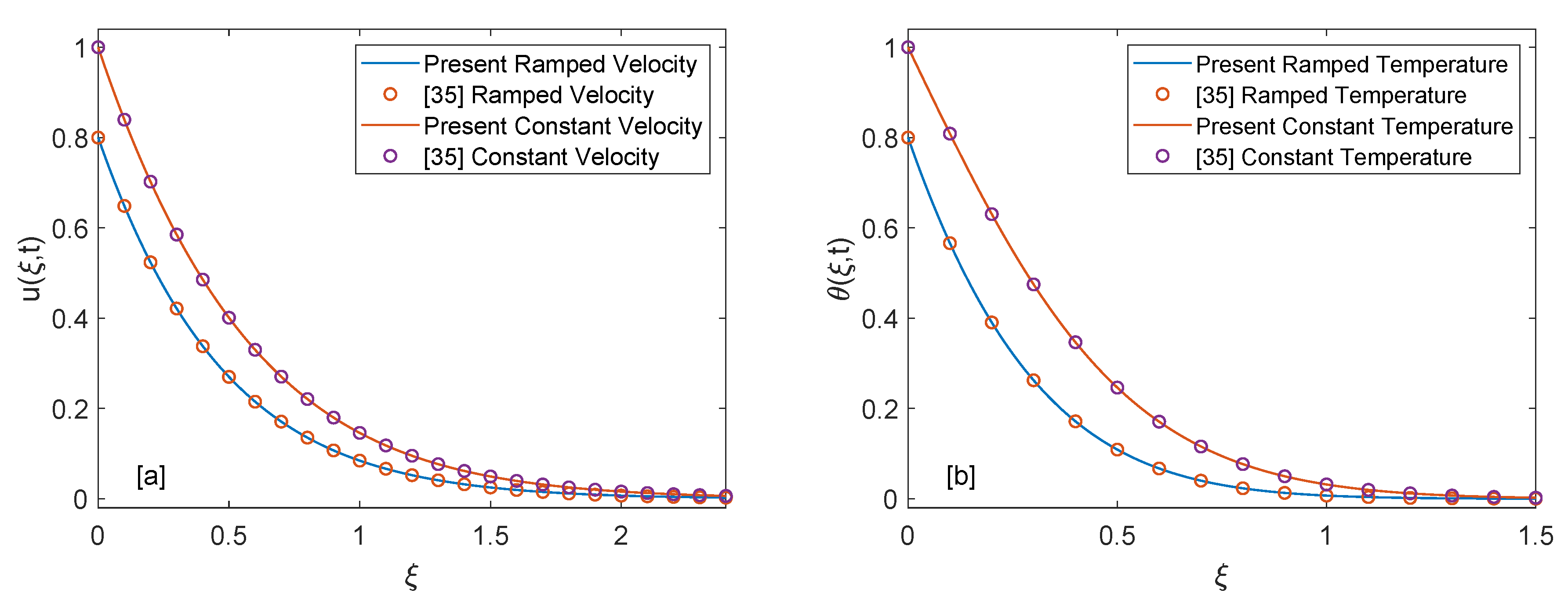
5. Results and Discussion
6. Conclusions
- Mass profile gets elevation with increase in , Gr, K, and . Oppositely, an increase in relaxation time and magnetic parameter M decelerate the flow.
- An increase in the amount of heat injection and volume fraction of nanoparticles enhances the temperature, while an inverse behavior is witnessed for the increase in the amount of heat suction.
- Heat transfer enhances when the volume fraction of CNTs increases. The values of are calculated using model proposed by Xue [44]. It is found that maximization in volume fraction boosts the thermal conductivity, which results in a higher rate of heat transfer.
- Velocity on the plate (skin friction) increases with an increase in retardation time and behaves oppositely for relaxation time and volume fraction .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. London. Ser. Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar]
- Heymans, N.; Bauwens, J.C. Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheol. Acta 1994, 33, 210–219. [Google Scholar] [CrossRef]
- Maxwell, J.C. Iv. on the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar]
- Das, K.; Chakraborty, T.; Kundu, P.K. Effect of magnetic field on Oldroyd-B type nanofluid flow over a permeable stretching surface. Propuls. Power Res. 2018, 7, 238–246. [Google Scholar] [CrossRef]
- Rao, A.S.; Nagendra, N. Thermal radiation effects on Oldroyd-B nano fluid from a stretching sheet in a non-Darcy porous medium. Glob. J. Pure Appl. Math. (GJPAM) 2015, 11, 2015. [Google Scholar]
- Gupta, S.; Gupta, S. MHD three dimensional flow of Oldroyd-B nanofluid over a bidirectional stretching sheet: DTM-Padé Solution. Nonlinear Eng. 2019, 8, 744–754. [Google Scholar] [CrossRef]
- Awad, F.G.; Ahamed, S.M.; Sibanda, P.; Khumalo, M. The effect of thermophoresis on unsteady Oldroyd-B nanofluid flow over stretching surface. PLoS ONE 2015, 10, e0135914. [Google Scholar] [CrossRef]
- Khan, W.A.; Khan, M.; Malik, R. Three-dimensional flow of an Oldroyd-B nanofluid towards stretching surface with heat generation/absorption. PLoS ONE 2014, 9, e105107. [Google Scholar]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Al-Mdallal, Q.M. Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 2017, 7, 2445. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab: San Francisco, CA, USA, 1995. [Google Scholar]
- Aaiza, G.; Khan, I.; Shafie, S. Energy transfer in mixed convection MHD flow of nanofluid containing different shapes of nanoparticles in a channel filled with saturated porous medium. Nanoscale Res. Lett. 2015, 10, 490. [Google Scholar] [CrossRef]
- Hussanan, A.; Khan, I.; Hashim, H.; Anuar, M.K.; Ishak, N.; Sarif, N.M.; Salleh, M.Z. Unsteady MHD flow of some nanofluids past an accelerated vertical plate embedded in a porous medium. J. Teknol. 2016, 78, 121–126. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Seyyedi, S.; Ganji, D.; Rokni, H.B.; Soleimani, S. Application of LBM in simulation of natural convection in a nanofluid filled square cavity with curve boundaries. Powder Technol. 2013, 247, 87–94. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D. Lattice Boltzmann method for MHD natural convection heat transfer using nanofluid. Powder Technol. 2014, 254, 82–93. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Vajravelu, K. Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3–water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder. Int. J. Heat Mass Transf. 2015, 80, 16–25. [Google Scholar] [CrossRef]
- Eid, M.R.; Al-Hossainy, A.; Zoromba, M.S. FEM for Blood-Based SWCNTs Flow Through a Circular Cylinder in a Porous Medium with Electromagnetic Radiation. Commun. Theor. Phys. 2019, 71, 1425. [Google Scholar] [CrossRef]
- Boumaiza, N.; Kezzar, M.; Eid, M.R.; Tabet, I. On numerical and analytical solutions for mixed convection Falkner-Skan flow of nanofluids with variable thermal conductivity. Waves Random Complex Media 2019, 1–20. [Google Scholar] [CrossRef]
- Lahmar, S.; Kezzar, M.; Eid, M.R.; Sari, M.R. Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Phys. Stat. Mech. Its Appl. 2020, 540, 123138. [Google Scholar] [CrossRef]
- Eid, M.R. Effects of NP Shapes on Non-Newtonian Bio-Nanofluid Flow in Suction/Blowing Process with Convective Condition: Sisko Model. J.-Non-Equilib. Thermodyn. 2019. [Google Scholar] [CrossRef]
- Kundu, B. Exact analysis for propagation of heat in a biological tissue subject to different surface conditions for therapeutic applications. Appl. Math. Comput. 2016, 285, 204–216. [Google Scholar] [CrossRef]
- Sobral Filho, D.C.; Barbosa e Silva, O. A new proposal to guide velocity and inclination in the ramp protocol for the treadmill ergometer. Arq. Bras. Cardiol. 2003, 81, 48–53. [Google Scholar]
- Ästrand, P.; Rodahl, K. Avaliação da capacidade de trabalho físico na base dos testes. In Tratado de Fisiologia do Exercício, 2nd ed.; Interamericana: Rio de Janeiro, Brazil, 1977; pp. 304–336. [Google Scholar]
- Bruce, R. Evaluation of functional capacity and exercise tolerance of cardiac patients. Mod. Concepts Cardiovasc. Dis. 1956, 25, 321. [Google Scholar] [PubMed]
- Myers, J.; Bellin, D. Ramp exercise protocols for clinical and cardiopulmonary exercise testing. Sport. Med. 2000, 30, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, N.; Dutta, M. Transient mass transfer flow past an impulsively started infinite vertical plate with ramped plate velocity and ramped temperature. Int. J. Phys. Sci. 2013, 8, 254–263. [Google Scholar]
- Seth, G.; Hussain, S.; Sarkar, S. Hydromagnetic natural convection flow with heat and mass transfer of a chemically reacting and heat absorbing fluid past an accelerated moving vertical plate with ramped temperature and ramped surface concentration through a porous medium. J. Egypt. Math. Soc. 2015, 23, 197–207. [Google Scholar] [CrossRef]
- Seth, G.; Sharma, R.; Sarkar, S. Natural Convection Heat and Mass Transfer Flow with Hall Current, Rotation, Radiation and Heat Absorption Past an Accelerated Moving Vertical Plate with Ramped Temperature. J. Appl. Fluid Mech. 2015, 8, 7–20. [Google Scholar]
- Seth, G.; Sarkar, S. MHD natural convection heat and mass transfer flow past a time dependent moving vertical plate with ramped temperature in a rotating medium with Hall effects, radiation and chemical reaction. J. Mech. 2015, 31, 91–104. [Google Scholar] [CrossRef]
- Narahari, M.; Bég, O.A.; Ghosh, S.K. Mathematical modelling of mass transfer and free convection current effects on unsteady viscous flow with ramped wall temperature. World J. Mech. 2011, 1, 176–184. [Google Scholar] [CrossRef]
- Chandran, P.; Sacheti, N.C.; Singh, A.K. Natural convection near a vertical plate with ramped wall temperature. Heat Mass Transf. 2005, 41, 459–464. [Google Scholar] [CrossRef]
- Mohd Zin, N.A.; Khan, I.; Shafie, S. Influence of thermal radiation on unsteady MHD free convection flow of Jeffrey fluid over a vertical plate with ramped wall temperature. Math. Probl. Eng. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Khan, I. A note on exact solutions for the unsteady free convection flow of a Jeffrey fluid. Z. Naturforsch. 2015, 70, 397–401. [Google Scholar] [CrossRef]
- Maqbool, K.; Mann, A.; Tiwana, M. Unsteady MHD convective flow of a Jeffery fluid embedded in a porous medium with ramped wall velocity and temperature. Alex. Eng. J. 2018, 57, 1071–1078. [Google Scholar] [CrossRef]
- Tiwana, M.H.; Mann, A.B.; Rizwan, M.; Maqbool, K.; Javeed, S.; Raza, S.; Khan, M.S. Unsteady Magnetohydrodynamic Convective Fluid Flow of Oldroyd-B Model Considering Ramped Wall Temperature and Ramped Wall Velocity. Mathematics 2019, 7, 676. [Google Scholar] [CrossRef]
- Schetz, J. On the approximate solution of viscous-flow problems. J. Appl. Mech. 1963, 30, 263–268. [Google Scholar] [CrossRef]
- Hayday, A.A.; Bowlus, D.A.; McGraw, R.A. Free convection from a vertical flat Plate with step discontinuities in surface temperature. J. Heat Transf. 1967, 89, 244–249. [Google Scholar] [CrossRef]
- Malhotra, C.P.; Mahajan, R.L.; Sampath, W.; Barth, K.L.; Enzenroth, R.A. Control of temperature uniformity during the manufacture of stable thin-film photovoltaic devices. Int. J. Heat Mass Transf. 2006, 49, 2840–2850. [Google Scholar] [CrossRef]
- Rajagopal, K.; Ruzicka, M.; Srinivasa, A. On the Oberbeck-Boussinesq approximation. Math. Model. Methods Appl. Sci. 1996, 6, 1157–1167. [Google Scholar] [CrossRef]
- Hayat, T.; Siddiqui, A.M.; Asghar, S. Some simple flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2001, 39, 135–147. [Google Scholar] [CrossRef]
- Asghar, S.; Parveen, S.; Hanif, S.; Siddiqui, A.M.; Hayat, T. Hall effects on the unsteady hydromagnetic flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2003, 41, 609–619. [Google Scholar] [CrossRef]
- Loganathan, P.; Nirmal Chand, P.; Ganesan, P. Radiation effects on an unsteady natural convective flow of a nanofluid past an infinite vertical plate. Nano 2013, 8, 1350001. [Google Scholar] [CrossRef]
- Das, S.; Jana, R. Natural convective magneto-nanofluid flow and radiative heat transfer past a moving vertical plate. Alex. Eng. J. 2015, 54, 55–64. [Google Scholar] [CrossRef]
- Xue, Q. Model for thermal conductivity of carbon nanotube-based composites. Phys. Condens. Matter 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Le Page, W.R. Complex Variables and the Laplace Ttransform for Engineers; Courier Corporation: North Chelmsford, MA, USA, 1980. [Google Scholar]
- Durbin, F. Numerical inversion of Laplace transforms: An efficient improvement to Dubner and Abate’s method. Comput. J. 1974, 17, 371–376. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Ali, F.; ul Karim, F.; Imran, M. MHD flow of Sodium Alginate-based Casson type nanofluid passing through a porous medium with Newtonian heating. Sci. Rep. 2018, 8, 8645. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S.; Tlili, I. Case study of MHD blood flow in a porous medium with CNTS and thermal analysis. Case Stud. Therm. Eng. 2018, 12, 374–380. [Google Scholar] [CrossRef]











| Physical Properties | Sodium Alginate | SWCNTs | MWCNTs |
|---|---|---|---|
| k (W/m K) | 0.613 | 6600 | 3000 |
| 989 | 2600 | 1600 | |
| (J/kg K) | 4175 | 425 | 796 |
| (1/K) | 0.99 | 27 | 44 |
| Volume Fraction | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 |
| Thermal Conductivity for SWCNT | 0.145 | 0.174 | 0.204 | 0.235 | 0.266 |
| Thermal Conductivity for MWCNT | 0.145 | 0.172 | 0.2 | 0.228 | 0.257 |
| t | Q | Nu for SWCNT | Nu for MWCNT | |
|---|---|---|---|---|
| 0.6 | 0.5 | 0.02 | 3.0803 | 3.0438 |
| 0.7 | - | - | 3.2597 | 3.2212 |
| 0.8 | - | - | 3.4120 | 3.3717 |
| 0.8 | −1 | - | 4.9698 | 4.9097 |
| - | −0.5 | - | 4.4898 | 4.4358 |
| - | 0 | - | 3.9728 | 3.9253 |
| - | 0.5 | - | 3.4120 | 3.3717 |
| - | 1 | - | 2.7988 | 2.7664 |
| - | 0.5 | 0.0 | 3.0099 | 3.0099 |
| - | - | 0.02 | 3.4120 | 3.3717 |
| - | - | 0.04 | 3.7718 | 3.6994 |
| y | t | Q | Temperature of SWCNTs | Temperature of MWCNTs | |
|---|---|---|---|---|---|
| 0.3 | 0.8 | 0.5 | 0.0 | 0.2040 | 0.2040 |
| - | - | - | 0.02 | 0.2521 | 0.2477 |
| - | - | - | 0.04 | 0.2923 | 0.2851 |
| - | - | −1 | 0.02 | 0.1741 | 0.1704 |
| - | - | −0.5 | - | 0.1958 | 0.1920 |
| - | - | 0 | - | 0.2215 | 0.2174 |
| - | - | 0.5 | - | 0.2521 | 0.2477 |
| - | - | 1 | - | 0.2886 | 0.2840 |
| - | 0.6 | 0.5 | - | 0.1475 | 0.1444 |
| - | 0.7 | - | - | 0.1975 | 0.1937 |
| - | 0.8 | - | - | 0.2521 | 0.2477 |
| 0.4 | 0.8 | - | - | 0.1581 | 0.1541 |
| 0.5 | - | - | - | 0.0950 | 0.0918 |
| 0.6 | - | - | - | 0.0547 | 0.0523 |
| y | t | M | Gr | K | Velocity for SWCNT | Velocity for MWCNT | |||
|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.8 | 0.02 | 2.0 | 1.0 | 0.6 | 1.0 | 1.0 | 0.4336 | 0.4350 |
| 0.4 | - | - | - | - | - | - | - | 0.3484 | 0.3499 |
| 0.5 | - | - | - | - | - | - | - | 0.2785 | 0.2800 |
| 0.3 | 0.6 | - | - | - | - | - | - | 0.3098 | 0.3110 |
| - | 0.7 | - | - | - | - | - | - | 0.3713 | 0.3726 |
| - | 0.8 | - | - | - | - | - | - | 0.4336 | 0.4350 |
| - | 0.8 | 0.0 | - | - | - | - | - | 0.4180 | 0.4180 |
| - | - | 0.02 | - | - | - | - | - | 0.4336 | 0.4350 |
| - | - | 0.04 | - | - | - | - | - | 0.4483 | 0.4511 |
| - | - | 0.02 | 2.0 | - | - | - | - | 0.4336 | 0.4350 |
| - | - | - | 4.0 | - | - | - | - | 0.3848 | 0.3862 |
| - | - | - | 6.0 | - | - | - | - | 0.3466 | 0.3480 |
| - | - | - | 2.0 | 1.0 | - | - | - | 0.4336 | 0.4350 |
| - | - | - | - | 2.0 | - | - | - | 0.4604 | 0.4620 |
| - | - | - | - | 3.0 | - | - | - | 0.4872 | 0.4889 |
| - | - | - | - | 1.0 | 0.1 | - | - | 0.4336 | 0.4350 |
| - | - | - | - | - | 0.4 | - | - | 0.4604 | 0.4620 |
| - | - | - | - | - | 0.9 | - | - | 0.4872 | 0.4889 |
| - | - | - | - | - | 0.6 | 1.0 | - | 0.4336 | 0.4350 |
| - | - | - | - | - | - | 2.0 | - | 0.3924 | 0.3943 |
| - | - | - | - | - | - | 3.0 | - | 0.3601 | 0.3622 |
| - | - | - | - | - | - | 1.0 | 1.0 | 0.4336 | 0.4350 |
| - | - | - | - | - | - | - | 2.0 | 0.4662 | 0.4673 |
| - | - | - | - | - | - | - | 3.0 | 0.4837 | 0.4845 |
| t | M | K | Shear Stress for SWCNT | Shear Stress for MWCNT | |||
|---|---|---|---|---|---|---|---|
| 0.6 | 0.02 | 2.0 | 0.6 | 1.0 | 1.0 | −1.5388 | −1.5308 |
| 0.7 | - | - | - | - | - | −1.7952 | −1.7859 |
| 0.8 | - | - | - | - | - | −2.0517 | −2.0411 |
| 0.8 | 0.0 | - | - | - | - | −1.9546 | −1.9546 |
| - | 0.02 | - | - | - | - | −2.0517 | −2.0411 |
| - | 0.04 | - | - | - | - | −2.1544 | −2.1329 |
| - | 0.02 | 2.0 | - | - | - | −2.0517 | −2.0411 |
| - | - | 4.0 | - | - | - | −2.3745 | −2.3628 |
| - | - | 6.0 | - | - | - | −2.6583 | −2.6457 |
| - | - | 2.0 | 0.1 | - | - | −3.1796 | −3.1727 |
| - | - | - | 0.4 | - | - | −2.1907 | −2.1808 |
| - | - | - | 0.9 | - | - | −1.9535 | −1.9423 |
| - | - | - | 0.6 | 1.0 | - | −2.0517 | −2.0411 |
| - | - | - | - | 2.0 | - | −1.4781 | −1.4695 |
| - | - | - | - | 3.0 | - | −1.2047 | −1.1972 |
| - | - | - | - | 1.0 | 2.0 | −2.9071 | −2.8946 |
| - | - | - | - | - | 3.0 | −3.7164 | −2.8946 |
| - | - | - | - | - | 4.0 | −4.5045 | −4.4899 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, T.; Kumam, P.; Khan, I.; Watthayu, W. Heat Transfer Enhancement in Unsteady MHD Natural Convective Flow of CNTs Oldroyd-B Nanofluid under Ramped Wall Velocity and Ramped Wall Temperature. Entropy 2020, 22, 401. https://doi.org/10.3390/e22040401
Anwar T, Kumam P, Khan I, Watthayu W. Heat Transfer Enhancement in Unsteady MHD Natural Convective Flow of CNTs Oldroyd-B Nanofluid under Ramped Wall Velocity and Ramped Wall Temperature. Entropy. 2020; 22(4):401. https://doi.org/10.3390/e22040401
Chicago/Turabian StyleAnwar, Talha, Poom Kumam, Ilyas Khan, and Wiboonsak Watthayu. 2020. "Heat Transfer Enhancement in Unsteady MHD Natural Convective Flow of CNTs Oldroyd-B Nanofluid under Ramped Wall Velocity and Ramped Wall Temperature" Entropy 22, no. 4: 401. https://doi.org/10.3390/e22040401
APA StyleAnwar, T., Kumam, P., Khan, I., & Watthayu, W. (2020). Heat Transfer Enhancement in Unsteady MHD Natural Convective Flow of CNTs Oldroyd-B Nanofluid under Ramped Wall Velocity and Ramped Wall Temperature. Entropy, 22(4), 401. https://doi.org/10.3390/e22040401






