Simulation of S-Entropy Production during the Transport of Non-Electrolyte Solutions in the Double-Membrane System
Abstract
1. Introduction
2. Theory
2.1. Membrane System
2.2. Model Equations
3. Results and Discussion
4. Conclusions
- We created nonlinear model equations of the concentration in the inter-membrane compartment (Cm), volume flux (Jv), solute flux (Js), and S-entropy produced by Jv, and by Js for binary homogeneous, non-electrolyte solutions. The created model equations, illustrated by Equations (12)–(15), consist of quadratic equations describing the concentration in the inter-membrane compartment (Cm), volume flux (Jv), and solute flux (Js) through the double-membrane system.
- The double-membrane system, composed of two membranes (Ml, Mr), separates the compartments l, m, and r containing the homogeneous, non-electrolyte binary solutions. The compartment m consists of the infinitesimal layer of the solution and its volume fulfills the condition Vm → 0. The volume of the compartments l and r fulfills the condition Vl = Vr → ∞. At the initial moment, the solution concentrations in the cell satisfy the condition Cl < Cm < Cr.
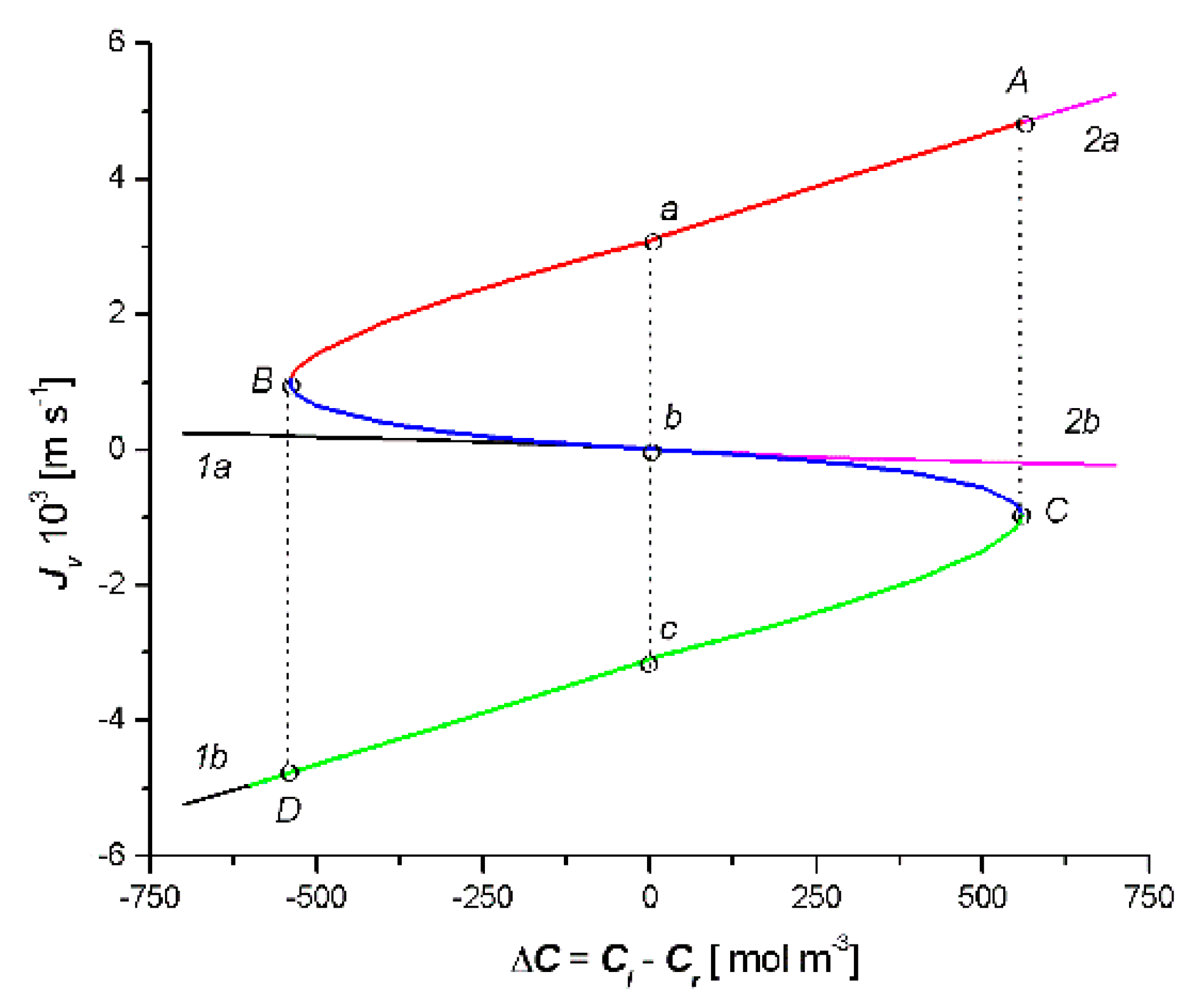
- Based on this model, for the fixed values of the reflection (σl, σr), hydraulic permeability (Lpl, Lpr), and solute permeability (ωl, ωr) coefficients, the dependencies Cm = f(Cl − Cr), Jv = f(Cl − Cr) and Js = f(Cl − Cr) were calculated. Each of the obtained characteristics was specifically arranged as a pair of parabolas.
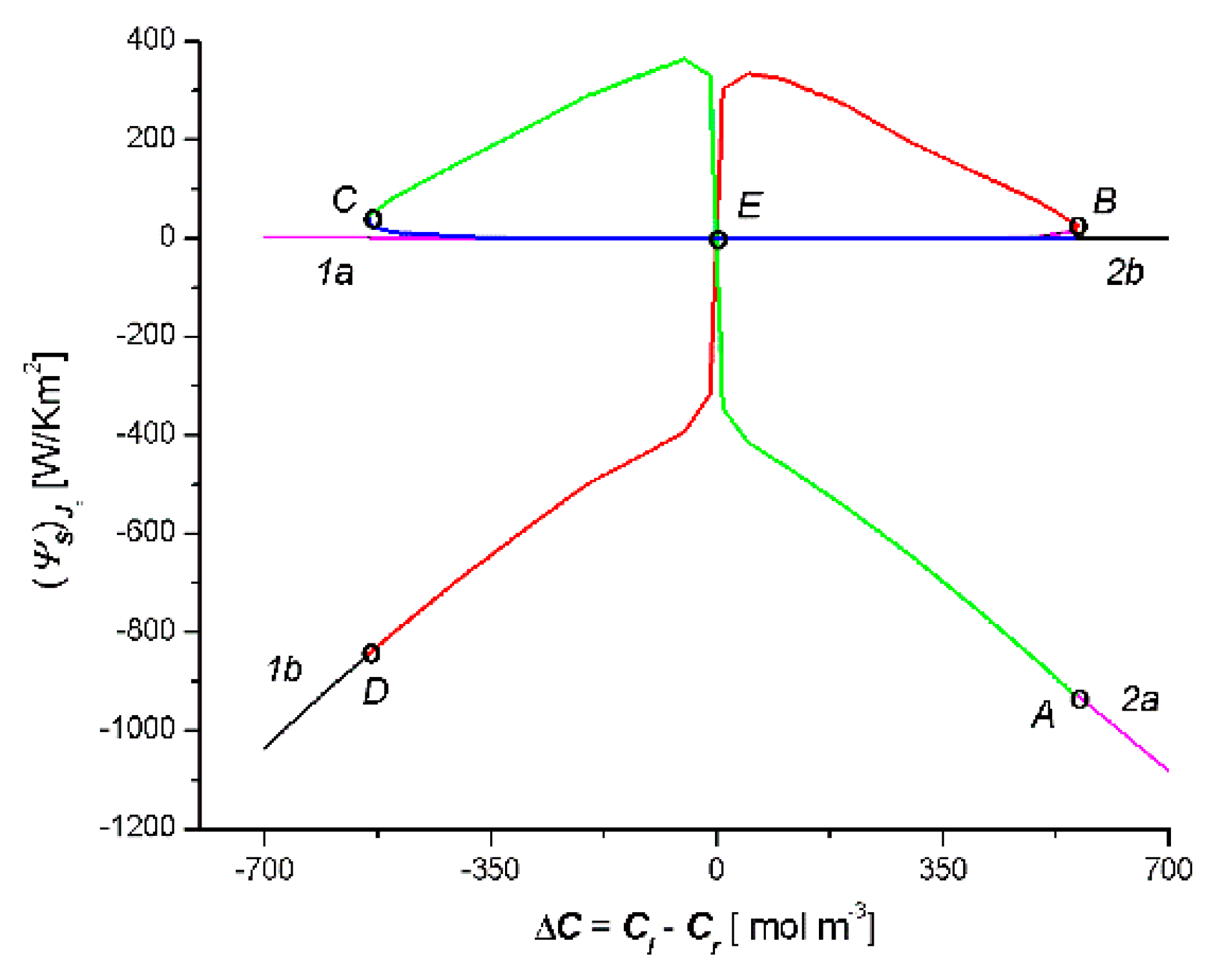
- The relationship = f(Cl − Cr) was a combination of two curves, 1a1b and 2a2b (two crossed bows in the shape of an inverted V), which intersected at the point with the coordinates = 0 and ΔC = 0. The sign was the consequence of the sign Jv and ΔC: > 0 when simultaneously Jv > 0 and ΔC > 0, or when simultaneously Jv < 0 and ΔC < 0. If simultaneously Jv < 0 and ΔC > 0 or when simultaneously Jv < 0 and ΔC > 0, then < 0. In turn, the relationship = f(Cl − Cr) is a bow in the shape of a jellyfish. The sign was the consequence of the sign Js and ΔC: > 0 when simultaneously Js > 0 and ΔC > 0 or when simultaneously Js < 0 and ΔC < 0. If simultaneously Js < 0 and ΔC > 0 or when simultaneously Js < 0 and ΔC > 0, then < 0. The cases < 0 and < 0 indicate a deviation from the second law of thermodynamics caused by the phenomenon of the accumulation or depletion of the dissolved substance in the inter-membrane compartment of the double-membrane system.
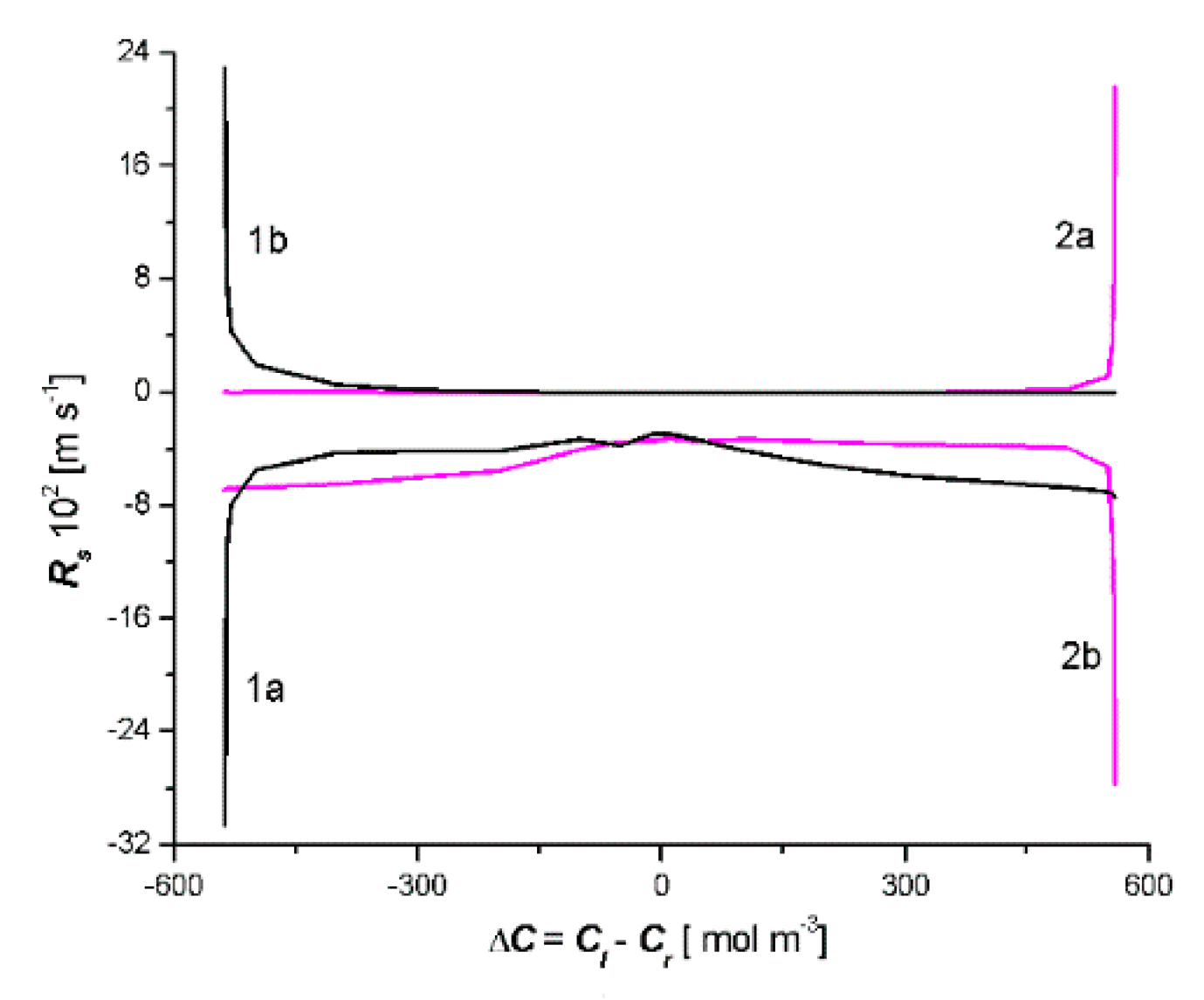
- In the solution concentration areas, where the relations were ΔC < 0, Jv > 0 and Js > 0, ΔC > 0, Jv < 0 and Js < 0, osmotic and diffusion transport (against the concentration gradient) occurred. In addition, in the areas where osmotic and diffusive transport took place (against the concentration gradient), osmotic and diffusion resistances (Rv, Rs) satisfied the conditions Rv < 0 and Rs < 0.
Author Contributions
Funding
Conflicts of Interest
References
- Demirel, Y. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems; Elsevier: Amsterdam, The Netherlands, 2014; pp. 275–540. ISBN 978-0-444-53079-0. [Google Scholar]
- Srivastava, R.C.; Saha, S.K.; Jain, A.K. Thermodynamics: A Core Course; PHI Learning: New Delhi, India, 2010; pp. 214–273. ISBN 978-81-203-3296-6. [Google Scholar]
- Delmotte, M.; Chanu, J. Non-equilibrium thermodynamics and membrane potential measurement in biology. In Topics Bioelectrochemistry and Bioenergetics; Millazzo, G., Ed.; John Wiley Publish & Sons: Chichester, UK, 1979; pp. 307–359. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Baker, R. Membrane Technology and Application; John Wiley & Sons: New York, NY, USA, 2012; ISBN 978-0-470-74372-0. [Google Scholar]
- Cheng, X.; Pinsky, P.M. The balance of fluid and osmotic pressures across active biological membranes with application to the corneal endothelium. PLoS ONE 2015, 10, e0145422. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jadhav, S.V.; Marathe, K.V.; Rathod, V.K. A pilot scale concurrent removal of fluoride, arsenic, sulfate and nitrate by using nanofiltration: Competing ion interaction and modelling approach. J. Water. Proc. Eng. 2016, 13, 153–167. [Google Scholar] [CrossRef]
- Teugels, L. Double Membrane Transducer Protector. U.S. Patent No 7,516,665 B2, 14 April 2009. [Google Scholar]
- Yan, Y.; Gu, S.; Gong, K. Double-Membrane Triple-Electrolyte Redox Flow Battery Design. U.S. Patent No. 9,917,323 B2, 13 March 2018. [Google Scholar]
- Curran, P.F.; McIntosh, J.R. A model system for biological water transport. Nature 1962, 193, 347–348. [Google Scholar] [CrossRef] [PubMed]
- Patlak, C.S.; Goldstein, D.; Hoffman, J.F. The flow of solute and solvent across a two-membrane system. J. Theor. Biol. 1963, 5, 426–442. [Google Scholar] [CrossRef]
- Richardson, I.W. Multiple membrane system as biological models (current-voltage behavior). J. Membr. Biol. 1972, 8, 219–236. [Google Scholar] [CrossRef] [PubMed]
- Ginsburg, H. Model for iso-osmotic water flow in plant roots. J. Theor. Biol. 1971, 32, 147–158. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. Permeability of composite membranes. Part 3. Series array of elements. Trans. Faraday Soc. 1963, 59, 1941–1953. [Google Scholar] [CrossRef]
- Katchalsky, A.; Curran, P.F. Nonequilibrium Thermodynamics in Biophysics; Harvard University Press: Cambridge, MA, USA, 1965; ISBN 9780674494121. [Google Scholar]
- Naparstek, A.; Caplan, S.R.; Katzir-Katchalsky, A. Series arrays of ion-exchange membranes concentration of electric current. Israel J. Chem. 1973, 11, 255–270. [Google Scholar] [CrossRef]
- Ohki, S. Rectification by double membranes. J. Phys. Sci. Jpn. 1965, 20, 1674–1685. [Google Scholar] [CrossRef]
- Tsukahara, S.; Nanzai, B.; Igawa, M. Selective transport of amino acids across a double membrane system composed of a cation- and an anion-exchange membrane. J. Membr. Sci. 2013, 448, 300–307. [Google Scholar] [CrossRef]
- Ueno, K.; Doi, T.; Nanzai, B.; Igawa, M. Selective transport of neutral amino acids across a double-membrane system comprising cation and anion exchange membranes. J. Membr. Sci. 2017, 537, 344–352. [Google Scholar] [CrossRef]
- Kargol, M.; Dworecki, K.; Przestalski, S. Graviosmotic flow amplification effects in a series membrane system. Stud. Biophys. 1979, 76, 137–144. [Google Scholar]
- Ślęzak, A.; Wasik, J.; Ślęzak, K. Effect of concentration boundary layers on mechanical pressure in a double-membrane system. Desalination 2004, 168, 423–433. [Google Scholar] [CrossRef]
- Ślęzak, A.; Wasik, J.; Grzegorczyn, S. Irreversible thermodynamics model equations for heterogeneous solute flux in a double-membrane system. Desalination 2004, 163, 155–175. [Google Scholar] [CrossRef]
- Ślęzak, A.; Jasik-Ślęzak, J.; Grzegorczyn, S.; Ślęzak-Prochazka, I. Nonlinear effects in osmotic volume flows of electrolyte solutions through double-membrane system. Transp. Porous Med. 2012, 92, 337–356. [Google Scholar] [CrossRef]
- Ślęzak, A.; Ślęzak-Prochazka, I.; Grzegorczyn, S.; Jasik-Ślęzak, J. Evaluation of S-Entropy production in a single-membrane system in concentration polarization conditions. Trans. Porous Med. 2017, 116, 941–957. [Google Scholar] [CrossRef]
- Rubin, A.B. Thermodynamics of Biological Processes; Moscow State University Press: Moscow, Russia, 1984. [Google Scholar]
- Weber, W.H.; Ford, G.W. Double injection in semiconductors heavily doped with deep two-level traps. Solid-State Electron. 1970, 13, 1333–1356. [Google Scholar] [CrossRef]
- Anderson, J.E. A model for current-controlled negative resistance in ion/membrane systems. J. Membr. Sci. 1978, 4, 35–40. [Google Scholar] [CrossRef]
- Abu-Rjal, R.; Prigozhin, L.; Rubinstein, I.; Zaltzman, B. Teorell instability in concentration polarization. Phys. Rev. E 2015, 92, 022305. [Google Scholar] [CrossRef] [PubMed]
- Franck, U.F. Phänomene an biologischen und künstlichen membrane. Berichte Bunsengess. 1967, 71, 789–799. [Google Scholar] [CrossRef]
- Cole, K.S. Membranes, Ions and Impulses; University California Press: Berkeley, CA, USA, 1968; ISBN 0-520-00252-2. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ślęzak, A.; Bajdur, W.M.; Batko, K.M.; Šcurek, R. Simulation of S-Entropy Production during the Transport of Non-Electrolyte Solutions in the Double-Membrane System. Entropy 2020, 22, 463. https://doi.org/10.3390/e22040463
Ślęzak A, Bajdur WM, Batko KM, Šcurek R. Simulation of S-Entropy Production during the Transport of Non-Electrolyte Solutions in the Double-Membrane System. Entropy. 2020; 22(4):463. https://doi.org/10.3390/e22040463
Chicago/Turabian StyleŚlęzak, Andrzej, Wioletta M. Bajdur, Kornelia M. Batko, and Radomir Šcurek. 2020. "Simulation of S-Entropy Production during the Transport of Non-Electrolyte Solutions in the Double-Membrane System" Entropy 22, no. 4: 463. https://doi.org/10.3390/e22040463
APA StyleŚlęzak, A., Bajdur, W. M., Batko, K. M., & Šcurek, R. (2020). Simulation of S-Entropy Production during the Transport of Non-Electrolyte Solutions in the Double-Membrane System. Entropy, 22(4), 463. https://doi.org/10.3390/e22040463







