Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model
Abstract
:1. Introduction
2. Fermi Distributions and Steric Potential
3. Fourth-Order Poisson-Bikerman Equation and Correlations
4. Generalized Gibbs Free Energy Functional
5. Poisson-Nernst-Planck-Bikerman Model of Saturating Phenomena
6. Generalized Debye-Hückel Theory
7. Numerical Methods
7.1. Nonlinear Iterative Methods
- Solve Laplace Equation for in once for all with on .
- Solve Poisson Equation for in with , on , and the jump condition on as (39), where V denotes applied voltage.
- an initial voltage.
- Solve 4PBik1 Equation for in with on , on , , , and .
- Solve 4PBik2 Equation for in with on and the same jump condition in Step 2, where is the derivative of with respect to .
- If the maximum error norm , a preset tolerance, then set and go to Step 4, else go to Step 7.
- Solve NP Equation for in for all with , , on , and on .
- Solve 4PBik1 Equation for as in Step 4 with in place of .
- Solve 4PBik2 Equation for as in Step 5.
- If , then set and go to Step 7, else go to Step 11.
- and go to Step 4 until the desired voltage is reached.
7.2. Discretization Methods
8. Applications
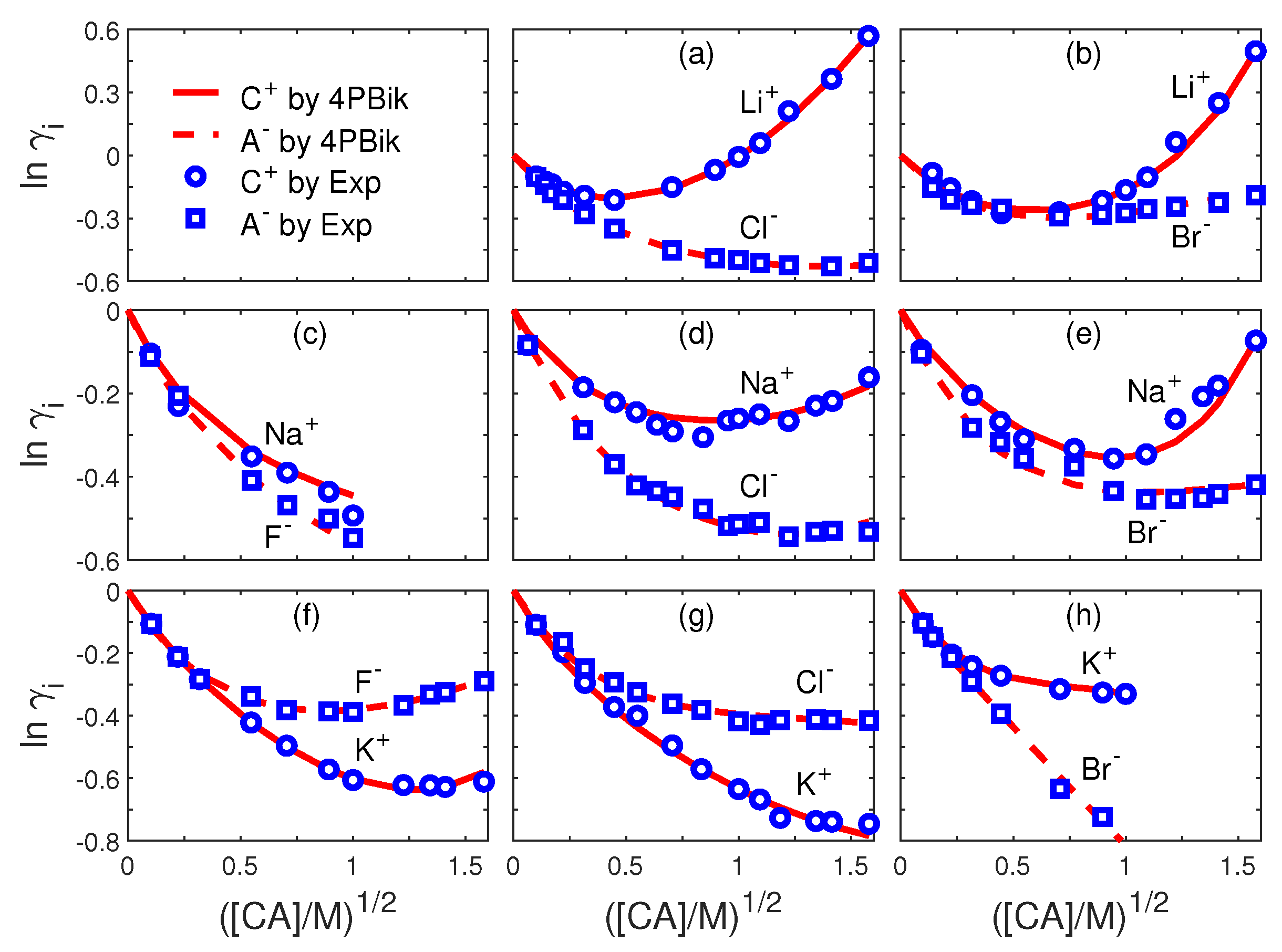
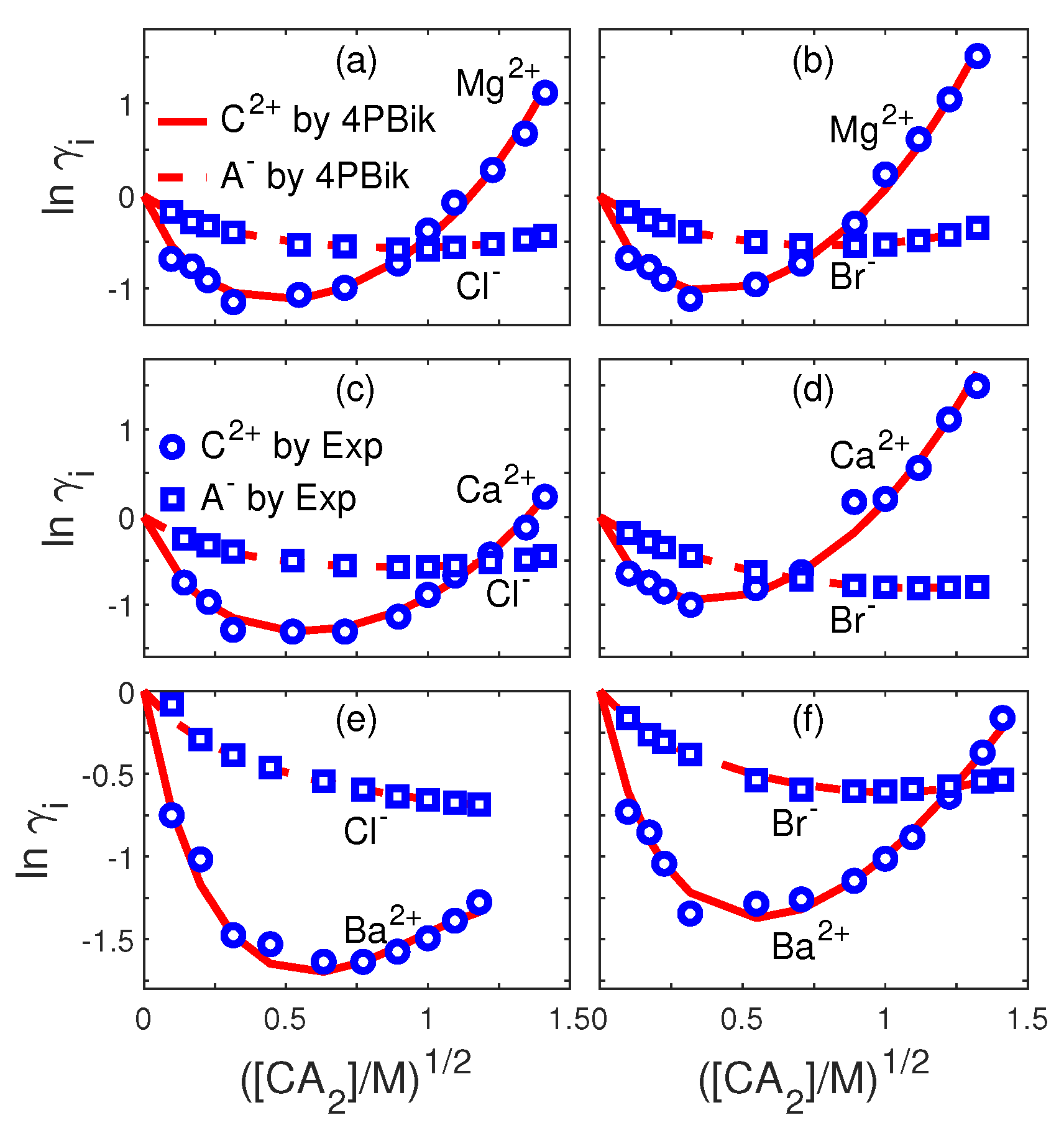
8.1. Ion Activities
8.2. Electric Double Layers
8.3. Biological Ion Channels
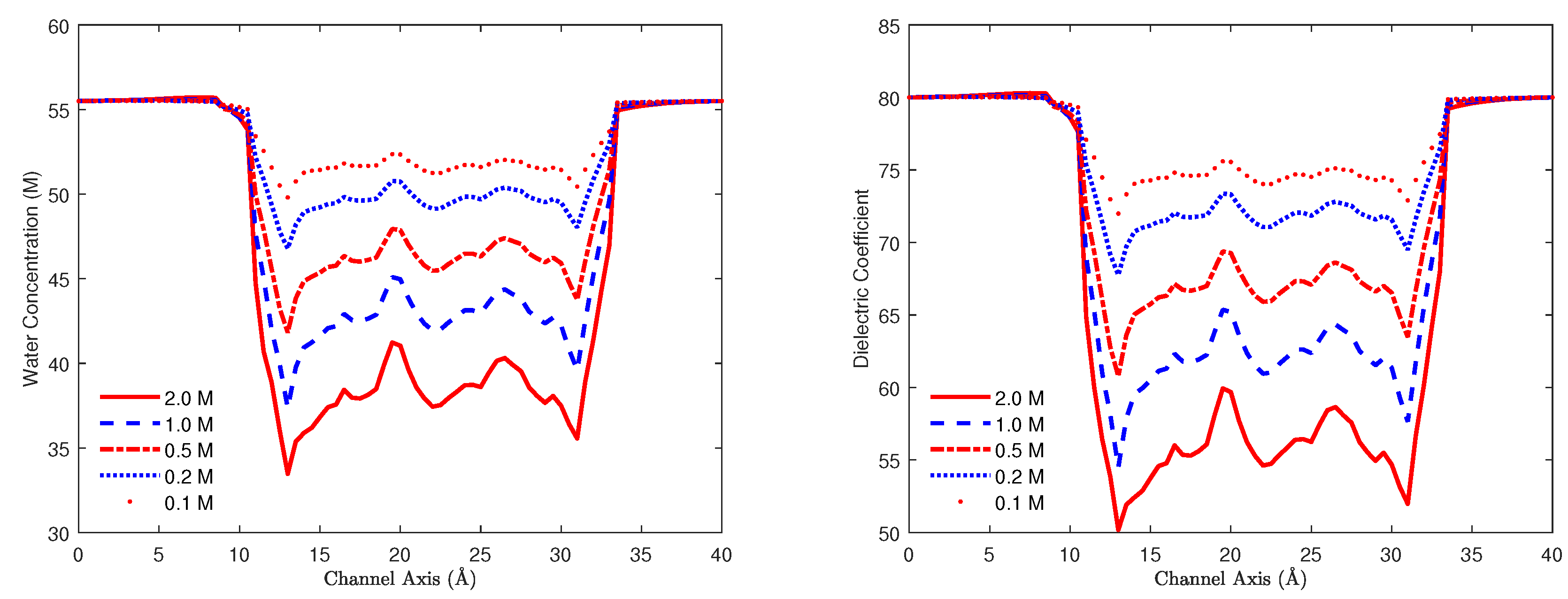
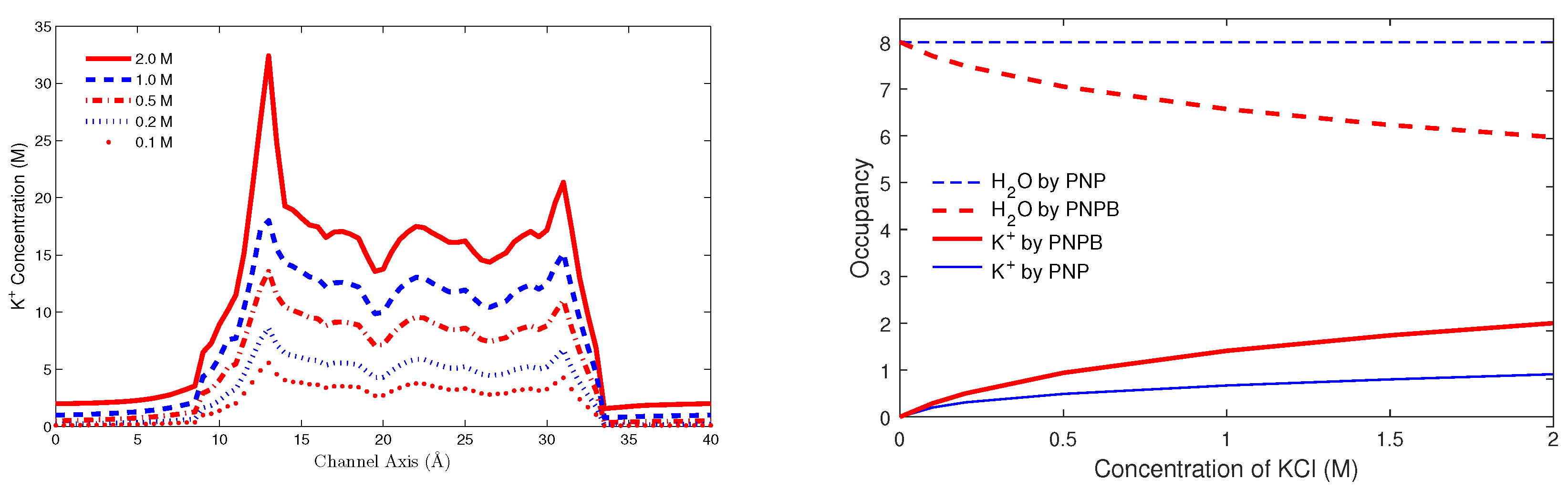
8.3.1. Gramicidin A Channel
8.3.2. L-Type Calcium Channel
8.3.3. Potassium Channel
8.3.4. Sodium Calcium Exchanger
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 4PBik | Fourth-Order Poisson-Bikerman |
| BD | Brownian Dynamics |
| bi-CG | bi-Conjugate Gradient Stabilized |
| DH | Debye-Hückel |
| EDL | Electric Double-Layer |
| FD | Finite Difference |
| GA | Gramicidin A |
| JESS | Joint Expert Speciation System |
| L-J | Lennard–Jones |
| MC | Monte Carlo |
| MD | Molecular Dynamics |
| NCX | Sodium Calcium Exchanger |
| NP | Nernst-Planck |
| ODE | Ordinary Differential Equation |
| OZ | Ornstein-Zernike |
| PB | Poisson–Boltzmann |
| PDE | Partial Differential Equation |
| PDB | Protein Data Bank |
| PNP | Poisson-Nernst-Planck |
| PNPB | Poisson-Nernst-Planck-Bikerman |
| SG | Scharfetter-Gummel |
| TPS | Total Potential State |
References
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions; Courier Corporation: North Chelmsford, MA, USA, 2002. [Google Scholar]
- Zemaitis, J.F.; Clark, D.M.; Rafal, M.; Scrivner, N.C. Handbook of Aqueous Electrolyte Thermodynamics; Design Institute for Physical Property Data, American Institute of Chemical Engineers: New York, NY, USA, 1986. [Google Scholar]
- Sharp, K.A.; Honig, B. Electrostatic interactions in macromolecules: Theory and applications. Annu. Rev. Biophys. Biophys. Chem. 1990, 19, 301–332. [Google Scholar] [CrossRef] [PubMed]
- Newman, J. Electrochemical Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Honig, B.; Nicholls, A. Classical electrostatics in biology and chemistry. Science 1995, 268, 1144–1149. [Google Scholar] [CrossRef] [Green Version]
- Pitzer, K.S. Thermodynamics; McGraw Hill: New York, NY, USA, 1995. [Google Scholar]
- Attard, P. Electrolytes and the electric double layer. Adv. Chem. Phys. 1996, 92, 1–159. [Google Scholar]
- Eisenberg, R.S. Computing the field in protein and channels. J. Membr. Biol. 1996, 150, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Hille, B. Ionic Channels of Excitable Membranes; Sinauer Associates Inc.: Sunderland, MA, USA, 2001. [Google Scholar]
- Fogolari, F.; Brigo, A.; Molinari, H. The Poisson-Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit. 2002, 15, 379–385. [Google Scholar] [CrossRef]
- Laidler, K.J.; Meiser, J.H.; Sanctuary, B.C. Physical Chemistry; Brooks Cole: Belmont, CA, USA, 2003. [Google Scholar]
- Fawcett, W.R. Liquids, Solutions, and Interfaces: From Classical Macroscopic Descriptions to Modern Microscopic Details; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Lebon, G.; Jou, D.; Casas-Vazquez, J. Understanding Non-Equilibrium Thermodynamics: Foundations, Applications, Frontiers; Springer: Berlin, Germany, 2008. [Google Scholar]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Coll. Interf. Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef] [Green Version]
- Kontogeorgis, G.M.; Folas, G.K. Thermodynamic Models for Industrial Applications: From Classical and Advanced Mixing Rules to Association Theories; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kunz, W. Specific Ion Effects; World Scientific: Singapore, 2010. [Google Scholar]
- Eisenberg, B. Crowded Charges in Ion Channels, Advances in Chemical Physics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 77–223. [Google Scholar]
- Hunenberger, P.; Reif, M. Single-Ion Solvation. Experimental and Theoretical Approaches to Elusive Thermodynamic Quantities; Royal Society of Chemistry: London, UK, 2011. [Google Scholar]
- Voigt, W. Chemistry of salts in aqueous solutions: Applications, experiments, and theory. Pure Appl. Chem. 2011, 83, 1015–1030. [Google Scholar] [CrossRef]
- Merlet, C.; Rotenberg, B.; Madden, P.A.; Taberna, P.L.; Simon, P.; Gogotsi, Y.; Salanne, M. On the molecular origin of supercapacitance in nanoporous carbon electrodes. Nat. Mater. 2012, 11, 306. [Google Scholar] [CrossRef]
- Wei, G.-W.; Zheng, Q.; Chen, Z.; Xia, K. Variational multiscale models for charge transport. SIAM Rev. 2012, 54, 699–754. [Google Scholar] [CrossRef] [Green Version]
- Fedorov, M.V.; Kornyshev, A.A. Ionic liquids at electrified interfaces. Chem. Rev. 2014, 114, 2978–3036. [Google Scholar] [CrossRef] [Green Version]
- Köpfer, D.A.; Song, C.; Gruene, T.; Sheldrick, G.M.; Zachariae, U.; de Groot, B.L. Ion permeation in K+ channels occurs by direct Coulomb knock-on. Science 2014, 346, 352–355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H., Jr.; Watanabe, M.; Simon, P.; Angell, A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; El-Din, T.M.G.; Payandeh, J.; Martinez, G.Q.; Heard, T.M.; Scheuer, T.; Zheng, N.; Catterall, W.A. Structural basis for Ca2+ selectivity of a voltage-gated calcium channel. Nature 2014, 505, 56–62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perreault, F.; De Faria, A.F.; Elimelech, M. Environmental applications of graphene-based nanomaterials. Chem. Soci. Rev. 2015, 44, 5861–5896. [Google Scholar] [CrossRef]
- Pilon, L.; Wang, H.; d’Entremont, A. Recent advances in continuum modeling of interfacial and transport phenomena in electric double layer capacitors. J. Electrochem. Soci. 2015, 162, A5158–A5178. [Google Scholar] [CrossRef] [Green Version]
- Shattock, M.J.; Ottolia, M.; Bers, D.M.; Blaustein, M.P.; Boguslavskyi, A.; Bossuyt, J.; Chen-Izu, Y.; Clancy, C.E.; Edwards, A.; Goldhaber, J.; et al. Na+/Ca2+ exchange and Na+/K+-ATPase in the heart. J. Physiol. 2015, 593, 1361–1382. [Google Scholar] [CrossRef] [Green Version]
- Zamponi, G.W.; Striessnig, J.; Koschak, A.; Dolphin, A.C. The physiology, pathology, and pharmacology of voltage-gated calcium channels and their future therapeutic potential. Pharmacol. Rev. 2015, 67, 821–870. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Trudeau, M.C. Handbook of Ion Channels; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Smith, A.M.; Lee, A.A.; Perkin, S. The electrostatic screening length in concentrated electrolytes increases with concentration. J. Phys. Chem. Lett. 2016, 7, 2157–2163. [Google Scholar] [CrossRef] [Green Version]
- Vera, J.H.; Wilczek-Vera, G. Classical Thermodynamics of Fluid Systems: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Faucher, S.; Aluru, N.; Bazant, M.Z.; Blankschtein, D.; Brozena, A.H.; Cumings, J.; de Souza, J.P.; Elimelech, M.; Epsztein, R.; Fourkas, J.T.; et al. Critical knowledge gaps in mass transport through single-digit nanopores: A review and perspective. J. Phys.Chem. C 2019, 123, 21309–21326. [Google Scholar] [CrossRef]
- Lian, T.; Koper, M.T.; Reuter, K.; Subotnik, J.E. Special topic on interfacial electrochemistry and photo(electro)catalysis. J. Chem. Phys. 2019, 150, 041401. [Google Scholar] [CrossRef] [Green Version]
- Chisholm, H.; Poisson, S.D. Encyclopadia Britannica; Cambridge University Press: Cambridge, UK, 1911; p. 896. [Google Scholar]
- Bjerrum, N.J.; Bohr, N. Niels Bjerrum: Selected Papers; Edited by Friends and Coworkers on the Occasion of His 70th Birthday the 11th of March, 1949; Munksgaard: Copenhagen, Denmark, 1949. [Google Scholar]
- Cercignani, C. The Boltzmann Equation and Its Applications; Springer: New York, NY, USA, 1988. [Google Scholar]
- Nernst, W. Die elektromotorische wirksamkeit der jonen. Z. Phys. Chem. 1889, 4, 129–181. [Google Scholar] [CrossRef]
- Planck, M. Ueber die erregung von electricität und warme in electrolyten. Ann. Der Phys. 1890, 275, 161–186. [Google Scholar] [CrossRef] [Green Version]
- Gouy, M. Sur la constitution de la charge electrique a la surface d’un electrolyte (Constitution of the electric charge at the surface of an electrolyte). J. Phys. 1910, 9, 457–468. [Google Scholar]
- Chapman, D.L. A contribution to the theory of electrocapillarity. Phil. Mag. 1913, 25, 475–481. [Google Scholar] [CrossRef] [Green Version]
- Bikerman, J.J. Structure and capacity of electrical double layer. Philos. Mag. 1942, 33, 384–397. [Google Scholar] [CrossRef]
- Eisenberg, R.; Chen, D. Poisson-Nernst-Planck (PNP) theory of an open ionic channel. Biophys. J. 1993, 64, A22. [Google Scholar]
- Shockley, W. Electrons and Holes in Semiconductors to Applications in Transistor Electronics; van Nostrand: New York, NY, USA, 1950. [Google Scholar]
- Van Roosbroeck, W. Theory of flow of electrons and holes in germanium and other semiconductors. Bell Syst. Tech. J. 1950, 29, 560–607. [Google Scholar] [CrossRef]
- Blotekjaer, K. Transport equations for electrons in two-valley semiconductors. IEEE Trans. Elec. Dev. 1970, 17, 38–47. [Google Scholar] [CrossRef]
- Kahng, D. A historical perspective on the development of MOS transistors and related devices. IEEE Trans. Elec. Dev. 1976, 23, 655–657. [Google Scholar] [CrossRef]
- Shockley, W. The path to the conception of the junction transistor. IEEE Trans. Elec. Dev. 1976, 23, 597–620. [Google Scholar] [CrossRef]
- Teal, G.K. Single crystals of germanium and silicon-Basic to the transistor and integrated circuit. IEEE Trans. Elec. Dev. 1976, 23, 621–639. [Google Scholar] [CrossRef]
- Selberherr, S. Analysis and Simulation of Semiconductor Devices; Springer: New York, NY, USA, 1984. [Google Scholar]
- Jacoboni, C.; Lugli, P. The Monte Carlo Method for Semiconductor Device Simulation; Springer: New York, NY, USA, 1989. [Google Scholar]
- Markowich, P.A.; Ringhofer, C.A.; Schmeiser, C. Semiconductor Equations; Springer: New York, NY, USA, 1990. [Google Scholar]
- Jerome, J.W. Analysis of Charge Transport. Mathematical Theory and Approximation of Semiconductor Models; Springer: New York, NY, USA, 1995. [Google Scholar]
- Ferry, D.K.; Goodnick, S.M.; Bird, J. Transport in Nanostructures; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Vasileska, D.; Goodnick, S.M.; Klimeck, G. Computational Electronics: Semiclassical and Quantum Device Modeling and Simulation; CRC Press: New York, NY, USA, 2010. [Google Scholar]
- Sakmann, B.; Neher, E. Single Channel Recording; Plenum: New York, NY, USA, 1995. [Google Scholar]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gross, L.; Mohn, F.; Moll, N.; Liljeroth, P.; Meyer, G. The chemical structure of a molecule resolved by atomic force microscopy. Science 2009, 325, 1110–1114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shklovskii, B.I. Screening of a macroion by multivalent ions: Correlation-induced inversion of charge. Phys. Rev. E 1999, 60, 5802–5811. [Google Scholar] [CrossRef] [Green Version]
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Prog. Phys. 2002, 65, 1577–1632. [Google Scholar] [CrossRef] [Green Version]
- Abrashkin, A.; Andelman, D.; Orland, H. Dipolar Poisson-Boltzmann equation: Ions and dipoles close to charge interfaces. Phys. Rev. Lett. 2007, 99, 077801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levy, A.; Andelman, D.; Orland, H. Dielectric constant of ionic solutions: A field-theory approach. Phys. Rev. Lett. 2012, 108, 227801. [Google Scholar] [CrossRef] [Green Version]
- Gavish, N.; Promislow, K. Dependence of the dielectric constant of electrolyte solutions on ionic concentration: A microfield approach. Phys. Rev. E 2016, 94, 012611. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-L. Numerical methods for the Poisson-Fermi equation in electrolytes. J. Comput. Phys. 2013, 247, 88–99. [Google Scholar] [CrossRef]
- Liu, J.-L.; Eisenberg, B. Correlated ions in a calcium channel model: A Poisson-Fermi theory. J. Phys. Chem. B 2013, 117, 12051–12058. [Google Scholar] [CrossRef]
- Liu, J.-L.; Eisenberg, B. Poisson-Nernst-Planck-Fermi theory for modeling biological ion channels. J. Chem. Phys. 2014, 141, 22D532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.-L.; Eisenberg, B. Analytical models of calcium binding in a calcium channel. J. Chem. Phys. 2014, 141, 075102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.-L.; Eisenberg, B. Numerical methods for a Poisson-Nernst-Planck-Fermi model of biological ion channels. Phys. Rev. E 2015, 92, 012711. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-L.; Eisenberg, B. Poisson-Fermi model of single ion activities in aqueous solutions. Chem. Phys. Lett. 2015, 637, 1–6. [Google Scholar] [CrossRef]
- Liu, J.-L.; Hsieh, H.-j.; Eisenberg, B. Poisson-Fermi modeling of the ion exchange mechanism of the sodium/calcium exchanger. J. Phys. Chem. B 2016, 120, 2658–2669. [Google Scholar] [CrossRef]
- Xie, D.; Liu, J.-L.; Eisenberg, B. Nonlocal Poisson-Fermi model for ionic solvent. Phys. Rev. E 2016, 94, 012114. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-L.; Xie, D.; Eisenberg, B. Poisson-Fermi formulation of nonlocal electrostatics in electrolyte solutions. Mol. Based Math. Biol. 2017, 5, 116–124. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-L.; Eisenberg, B. Poisson-Fermi modeling of ion activities in aqueous single and mixed electrolyte solutions at variable temperature. J. Chem. Phys. 2018, 148, 054501. [Google Scholar] [CrossRef]
- Chen, J.-H.; Chen, R.-C.; Liu, J.-L. A GPU Poisson-Fermi solver for ion channel simulations. Comput. Phys. Commun. 2018, 229, 99–105. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-L.; Li, C.-L. A generalized Debye-Huckel theory of electrolyte solutions. AIP Adv. 2019, 9, 015214. [Google Scholar] [CrossRef] [Green Version]
- Li, C.-L.; Liu, J.-L. Analysis of generalized Debye-Hückel equation from Poisson-Fermi theory. arXiv 2018, arXiv:1801.03470. [Google Scholar]
- Santangelo, C.D. Computing counterion densities at intermediate coupling. Phys. Rev. E 2006, 73, 041512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bazant, M.Z.; Storey, B.D.; Kornyshev, A.A. Double layer in ionic liquids: Overscreening versus crowding. Phys. Rev. Lett. 2011, 106, 046102. [Google Scholar] [CrossRef] [Green Version]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Karlin, S.; Taylor, H.E. A Second Course in Stochastic Processes; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 1926, 28, 1049. [Google Scholar] [CrossRef]
- Fermi, E. Sulla quantizzazione del gas perfetto monoatomico. Rend. Lincei 1926, arXiv:99122293, 145–149, Translated as Zannoni, A. On the quantization of the monoatomic ideal gas. arXiv 1999. [Google Scholar]
- Pauli, W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Z. Phys. 1925, 31, 765–783. [Google Scholar] [CrossRef]
- Van der Waals, J.D. Thermodynamische Theorie der Capillariteit in de Onderstelling van Continue Dichtheidsverandering; Verhand. Kon. Akad. V Wetensch. Amst. Sect. 1, 1893. (English Translation, The thermodynamik theory of capillarity under the hypothesis of a continuous variation of density. J. Stat. Phys. 1979, 20, 197. [Google Scholar]
- Hill, T.L. Steric effects. I. Van der Waals potential energy curves. J. Chem. Phys. 1948, 16, 399–404. [Google Scholar] [CrossRef]
- Regan, C.K.; Craig, S.L.; Brauman, J.I. Steric effects and solvent effects in ionic reactions. Science 2002, 295, 2245–2247. [Google Scholar] [CrossRef] [Green Version]
- Kornyshev, A.A. Double-layer in ionic liquids: Paradigm change? J. Phys. Chem. B 2007, 111, 5545–5557. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F.; Katz, B. Ionic currents underlying activity in the giant axon of the squid. Arch. Sci. Physiol. 1949, 3, 129–150. [Google Scholar]
- Bezanilla, F. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 2000, 80, 555–592. [Google Scholar] [CrossRef] [PubMed]
- Bezanilla, F.; Villalba-Galea, C.A. The gating charge should not be estimated by fitting a two-state model to a Q-V curve. J. Gen. Physiol. 2013, 142, 575–578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McQuarrie, D.A. Statistical Mechanics; Harper and Row: New York, NY, USA, 1976. [Google Scholar]
- Verlet, L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Heinz, H.; Vaia, R.A.; Farmer, B.L.; Naik, R.R. Accurate simulation of surfaces and interfaces of face-centered cubic metals using 12- 6 and 9- 6 Lennard-Jones potentials. J. Phys. Chem. C 2008, 112, 17281–17290. [Google Scholar] [CrossRef]
- Lu, B.; McCammon, J.A. Molecular surface-free continuum model for electrodiffusion processes. Chem. Phys. Lett. 2008, 451, 282–286. [Google Scholar] [CrossRef] [Green Version]
- Simakov, N.A.; Kurnikova, M.G. Soft wall ion channel in continuum representation with application to modeling ion currents in α-Hemolysin. J. Phys. Chem. B 2010, 114, 15180–15190. [Google Scholar] [CrossRef] [Green Version]
- Hyon, Y.K.; Fonseca, J.E.; Eisenberg, B.; Liu, C. Energy variational approach to study charge inversion (layering) near charged walls. Discret. Cont. Dyn. Sys. Ser. A 2012, 17, 2725–2743. [Google Scholar] [CrossRef]
- Horng, T.-L.; Lin, T.-C.; Liu, C.; Eisenberg, B. PNP equations with steric effects: A model of ion flow through channels. J. Phys. Chem. B 2012, 116, 11422–11441. [Google Scholar] [CrossRef]
- Maffeo, C.; Bhattacharya, S.; Yoo, J.; Wells, D.; Aksimentiev, A. Modeling and simulation of ion channels. Chem. Rev. 2012, 112, 6250–6284. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.-C.; Eisenberg, B. A new approach to the Lennard-Jones potential and a new model: PNP-steric equations. Commun. Math. Sci. 2014, 12, 149–173. [Google Scholar] [CrossRef] [Green Version]
- Gavish, N. Poisson–Nernst–Planck equations with steric effects—non-convexity and multiple stationary solutions. Physica D 2018, 368, 50–65. [Google Scholar] [CrossRef] [Green Version]
- Gavish, N.; Elad, D.; Yochelis, A. From solvent-free to dilute electrolytes: Essential components for a continuum theory. Phys. Chem. Lett. 2018, 9, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Zangwill, A. Modern Electrodynamics; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Eisenberg, B. Updating Maxwell with electrons, charge, and more realistic polarization. arXiv 2019, arXiv:1904.09695. [Google Scholar]
- Liu, J.-L. A quantum corrected Poisson-Nernst-Planck model for biological ion channels. Mol. Based Math. Biol. 2015, 3, 70–77. [Google Scholar] [CrossRef]
- Eisenberg, B.; Oriols, X.; Ferry, D. Dynamics of current, charge, and mass. Mol. Based Math. Biol. 2017, 5, 78–115. [Google Scholar] [CrossRef] [Green Version]
- Hildebrandt, A.; Blossey, R.; Rjasanow, S.; Kohlbacher, O.; Lenhof, H.-P. Novel formulation of nonlocal electrostatics. Phys. Rev. Lett. 2004, 93, 108104. [Google Scholar] [CrossRef] [Green Version]
- Rowlinson, J.S. The Yukawa potential. Physica A 1989, 156, 15–34. [Google Scholar] [CrossRef]
- Eisenberg, B. Dielectric dilemma. arXiv 2019, arXiv:1901.10805. [Google Scholar]
- Barthel, J.; Buchner, R.; Münsterer, M. Electrolyte Data Collection Vol. 12, Part 2: Dielectric Properties of Water and Aqueous Electrolyte Solutions; Frankfurt am Main: Dechema, Czech Republic, 1995. [Google Scholar]
- Buchner, R.; Barthel, J. Dielectric relaxation in solutions. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 2001, 97, 349–382. [Google Scholar] [CrossRef]
- Yukawa, H. On the interaction of elementary particles. I. Proc. Phys.-Math. Soc. Jpn. Ser. 1935, 17, 48–57. [Google Scholar]
- Rowlinson, J.S. Cohesion: A Scientific History of Intermolecular Forces; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ornstein, L.S.; Zernike, F. Accidental deviations of density and opalescence at the critical point of a single substance. R. Netherlands Acad. Arts Sci. Proc. 1914, 17, 793–806. [Google Scholar]
- Blossey, R.; Maggs, A.C.; Podgornik, R. Structural interactions in ionic liquids linked to higher-order Poisson-Boltzmann equations. Phys. Rev. E 2017, 95, 060602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Downing, R.; Berntson, B.K.; Bossa, G.V.; May, S. Differential capacitance of ionic liquids according to lattice-gas mean-field model with nearest-neighbor interactions. J. Chem. Phys. 2018, 149, 204703. [Google Scholar] [CrossRef] [PubMed]
- Kornyshev, A.A.; Sutmann, G. The shape of the nonlocal dielectric function of polar liquids and the implications for thermodynamic properties of electrolytes: A comparative study. J. Chem. Phys. 1996, 104, 1524. [Google Scholar] [CrossRef]
- Schutz, C.N.; Warshel, A. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins Struct. Funct. Bioinf. 2001, 44, 400–417. [Google Scholar] [CrossRef] [PubMed]
- Mallik, B.; Masunov, A.; Lazaridis, T. Distance and exposure dependent effective dielectric function. J. Comput. Chem. 2002, 23, 1090–1099. [Google Scholar] [CrossRef]
- Corry, B.; Kuyucak, S.; Chung, S.-H. Dielectric self-energy in Poisson-Boltzmann and Poisson-Nernst-Planck models of ion channels. Biophys. J. 2003, 84, 3594–3606. [Google Scholar] [CrossRef] [Green Version]
- Graf, P.; Kurnikova, M.G.; Coalson, R.D.; Nitzan, A. Comparison of dynamic lattice Monte Carlo simulations and the dielectric self-energy Poisson-Nernst-Planck continuum theory for model ion channels. J. Phys. Chem. B 2004, 108, 2006–2015. [Google Scholar] [CrossRef]
- Cheng, M.H.; Coalson, R.D. An accurate and efficient empirical approach for calculating the dielectric self-energy and ion-ion pair potential in continuum models of biological ion channels. J. Phys. Chem. B 2005, 4, 81–93. [Google Scholar] [CrossRef]
- Ng, J.A.; Vora, T.; Krishnamurthy, V.; Chung, S.-H. Estimating the dielectric constant of the channel protein and pore. Eur. Biophys. J. 2008, 37, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Silalahi, A.R.J.; Boschitsch, A.H.; Harris, R.C.; Fenley, M.O. Comparing the predictions of the nonlinear Poisson-Boltzmann equation and the ion size-modified Poisson-Boltzmann equation for a low-dielectric charged spherical cavity in an aqueous salt solution. J. Chem. Theory Comput. 2010, 6, 3631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopéz-García, J.J.; Horno, J.; Grosse, C. Poisson-Boltzmann description of the electrical double layer including ion size effects. Langmuir 2011, 27, 13970–13974. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, I. Effects of dielectric inhomogeneity and electrostatic correlation on the solvation energy of ions in liquids. J. Phys. Chem. B 2018, 122, 6064–6071. [Google Scholar] [CrossRef] [PubMed]
- Kjellander, R. Focus Article: Oscillatory and longrange monotonic exponential decays of electrostatic interactions in ionic liquids and other electrolytes: The significance of dielectric permittivity and renormalized charges. J. Chem. Phys. 2018, 148, 193701. [Google Scholar] [CrossRef] [PubMed]
- Fogolari, F.; Briggs, J.M. On the variational approach to Poisson–Boltzmann free energies. Chem. Phys. Lett. 1997, 281, 135–139. [Google Scholar] [CrossRef]
- Li, B. Minimization of electrostatic free energy and the Poisson-Boltzmann equation for molecular solvation with implicit solvent. SIAM J. Math. Anal. 2009, 40, 2536–2566. [Google Scholar] [CrossRef] [Green Version]
- Sharp, K.A.; Honig, B. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 1990, 94, 7684–7692. [Google Scholar] [CrossRef]
- Reiner, E.S.; Radke, C.J. Variational approach to the electrostatic free energy in charged colloidal suspensions: General theory for open systems. J. Chem. Soci. Faraday Trans. 1990, 86, 3901–3912. [Google Scholar] [CrossRef]
- Gilson, M.K.; Davis, M.E.; Luty, B.A.; McCammon, J.A. Computation of electrostatic forces on solvated molecules using the Poisson-Boltzmann equation. J. Phys. Chem. 1993, 97, 3591–3600. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orland, H. Steric effects in electrolytes: A modified Poisson-Boltzmann equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef] [Green Version]
- Ben-Yaakov, D.; Andelman, D.; Podgornik, R. Ion-specific hydration effects: Extending the Poisson-Boltzmann theory. Curr. Opin. Colloid Interface Sci. 2011, 16, 542–550. [Google Scholar] [CrossRef] [Green Version]
- Lu, B.; Zhou, Y.C. Poisson-Nernst-Planck equations for simulating biomolecular diffusion-reaction processes II: Size effects on ionic distributions and diffusion-reaction rates. Biophys. J. 2011, 100, 2475–2485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, S.; Wang, Z.; Li, B. Mean-field description of ionic size effects with non-uniform ionic sizes: A numerical approach. Phys. Rev. E 2011, 84, 021901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiao, Y.; Tu, B.; Lu, B. Ionic size effects to molecular solvation energy and to ion current across a channel resulted from the nonuniform size-modified PNP equations. J. Chem. Phys. 2014, 140, 174102. [Google Scholar] [CrossRef] [Green Version]
- Grimley, T.B.; Mott, N.F. The contact between a solid and a liquid electrolyte. Discuss. Faraday Soc. 1947, 1, 3–11. [Google Scholar] [CrossRef]
- Tresset, G. Generalized Poisson-Fermi formalism for investigating size correlation effects with multiple ions. Phys. Rev. E 2008, 78, 061506. [Google Scholar] [CrossRef]
- Bohinc, K.; Kralj-Iglič, V.; Iglič, A. Thickness of electrical double layer. Effect of ion size. Electrochim. Acta 2001, 46, 3033–3040. [Google Scholar] [CrossRef] [Green Version]
- McEldrew, M.; Goodwin, Z.A.; Kornyshev, A.A.; Bazant, M.Z. Theory of the double layer in water-in-salt electrolytes. Phys. Chem. Lett. 2018, 9, 5840–5846. [Google Scholar] [CrossRef] [Green Version]
- Maggs, A.C.; Podgornik, R. General theory of asymmetric steric interactions in electrostatic double layers. Soft Matter 2016, 12, 1219–1229. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.P.; Barcilon, V.; Eisenberg, R.S. Constant fields and constant gradients in open ionic channels. Biophys. J. 1992, 61, 1372–1393. [Google Scholar] [CrossRef] [Green Version]
- Eisenberg, R.S.; Kłosek, M.M.; Schuss, Z. Diffusion as a chemical reaction: Stochastic trajectories between fixed concentrations. J. Chem. Phys. 1995, 102, 1767–1780. [Google Scholar] [CrossRef]
- Eisenberg, B.; Hyon, Y.K.; Liu, C. Energy variational analysis EnVarA of ions in water and channels: Field theory for primitive models of complex ionic fluids. J. Chem. Phys. 2010, 133, 104104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.; Wu, H. An energetic variational approach for the Cahn–Hilliard equation with dynamic boundary condition: Model derivation and mathematical analysis. Arch. Ration. Mech. Anal. 2019, 233, 167–247. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Eisenberg, B.; Song, Z.; Huang, H. Osmosis through a semi-permeable membrane: A consistent approach to interactions. arXiv 2018, arXiv:1806.00646. [Google Scholar]
- Zhu, Y.; Xu, S.; Eisenberg, B.; Huang, H. A bidomain model for lens microcirculation. Biophys. J. 2019, 116, 1171–1184. [Google Scholar] [CrossRef] [Green Version]
- Debye, P.; Hückel, E. Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinunge (The theory of electrolytes. I. Lowering of freezing point and related phenomena). Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Hückel, E. Zur Theorie konzentrierterer wässeriger L ösungen starker Elektrolyte. Phys. Z. 1925, 26, 93–147. [Google Scholar]
- Myers, J.A.; Sandler, S.I.; Wood, R.H. An equation of state for electrolyte solutions covering wide ranges of temperature, pressure, and composition. Ind. Eng. Chem. Res. 2002, 41, 3282–3297. [Google Scholar] [CrossRef]
- Voigt, W.; Brendler, V.; Marsh, K.; Rarey, R.; Wanner, H.; Gaune-Escard, M.; Cloke, P.; Vercouter, T.; Bastrakov, E.; Hagemann, S. Quality assurance in thermodynamic databases for performance assessment studies in waste disposal. Pure Appl. Chem. 2007, 79, 883–894. [Google Scholar] [CrossRef]
- Rowland, D.; Königsberger, E.; Hefter, G.; May, P.M. Aqueous electrolyte solution modelling: Some limitations of the Pitzer equations. Appl. Geochem. 2015, 55, 170. [Google Scholar] [CrossRef] [Green Version]
- Kontogeorgis, G.M.; Maribo-Mogensen, B.; Thomsen, K. The Debye-Hückel theory and its importance in modeling electrolyte solutions. Fluid Phase Equil. 2018, 462, 130–152. [Google Scholar] [CrossRef] [Green Version]
- Bell, I.H.; Mickoleit, E.; Hsieh, C.M.; Lin, S.T.; Vrabec, J.; Breitkopf, C.; Jager, A. A Benchmark Open-Source Implementation of COSMO-SAC. J. Chem. Theory Comput. 2020. [Google Scholar] [CrossRef] [PubMed]
- Fraenkel, D. Simplified electrostatic model for the thermodynamic excess potentials of binary strong electrolyte solutions with size-dissimilar ions. Mol. Phys. 2010, 108, 1435. [Google Scholar] [CrossRef]
- May, P.M.; Rowland, D.; Murray, K.; May, E.F. JESS: Joint Expert Speciation System. Available online: http://jess.murdoch.edu.au/jess_home.htm (accessed on 13 May 2020).
- May, P.M.; Rowland, D.; Königsberger, E.; Hefter, G. JESS, a Joint Expert Speciation System—IV: A large database of aqueous solution physicochemical properties with an automatic means of achieving thermodynamic consistency. Talanta 2010, 81, 142–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stokes, R.H.; Robinson, R.A. Ionic hydration and activity in electrolyte solutions. J. Am. Chem. Soc. 1948, 70, 1870–1878. [Google Scholar] [CrossRef]
- Rashin, A.A.; Honig, B. Reevaluation of the Born model of ion hydration. J. Phys. Chem. 1985, 89, 5588–5593. [Google Scholar] [CrossRef]
- Marcus, Y. Thermodynamics of solvation of ions. Part 5.— Gibbs free energy of hydration at 298.15 K. J. Chem. Soc. Faraday Trans. 1991, 87, 2995–2999. [Google Scholar] [CrossRef]
- Ohtaki, H.; Radnai, T. Structure and dynamics of hydrated ions. Chem. Rev. 1993, 93, 1157–1204. [Google Scholar] [CrossRef]
- Babu, C.S.; Lim, C. Theory of ionic hydration: Insights from molecular dynamics simulations and experiment. J. Phys. Chem. B 1999, 103, 7958–7968. [Google Scholar] [CrossRef]
- Varma, S.; Rempe, S.B. Coordination numbers of alkali metal ions in aqueous solutions. Biophys. Chem. 2006, 124, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Mähler, J.; Persson, I. A study of the hydration of the alkali metal ions in aqueous solution. Inorg. Chem. 2011, 51, 425–438. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Irmer, G. Hydration of the calcium(II) ion in an aqueous solution of common anions (ClO4-, Cl−, Br−, and NO3−). Dalton Trans. 2013, 42, 3919. [Google Scholar] [CrossRef]
- Bashford, D.; Case, D.A. Generalized Born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000, 51, 129–152. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.P.; Fisher, M.E. Density fluctuations in an electrolyte from generalized Debye-Hueckel theory. Phys. Rev. Lett. 1996, 76, 2906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chern, I.-L.; Liu, J.-G.; Wang, W.-C. Accurate evaluation of electrostatics for macromolecules in solution. Methods Appl. Anal. 2003, 10, 309–328. [Google Scholar] [CrossRef]
- Geng, W.; Yu, S.; Wei, G. Treatment of charge singularities in implicit solvent models. J. Chem. Phys. 2007, 127, 114106. [Google Scholar] [CrossRef] [PubMed]
- de Souza, J.P.; Bazant, M.Z. Continuum theory of electrostatic correlations at charged surfaces. arXiv 2019, arXiv:1902.05493. [Google Scholar] [CrossRef]
- Misra, R.P.; de Souza, J.P.; Blankschtein, D.; Bazant, M.Z. Theory of surface forces in multivalent electrolytes. Langmuir 2019, 35, 11550–11565. [Google Scholar] [CrossRef] [Green Version]
- Valiskó, M.; Boda, D. Unraveling the behavior of the individual ionic activity coefficients on the basis of the balance of ion-ion and ion-water interactions. J. Phys. Chem. B 2015, 119, 1546. [Google Scholar] [CrossRef] [Green Version]
- Grenthe, I.; Puigdomenech, I. Modelling in Aquatic Chemistry; OECD Nuclear Energy Agency: Paris, France, 1997. [Google Scholar]
- Davies, C.W. The extent of dissociation of salts in water. Part VIII. An equation for the mean ionic activity coefficient of an electrolyte in water, and a revision of the dissociation constants of some sulphates. J. Chem. Soc. (Resumed) 1938, 2093–2098. [Google Scholar] [CrossRef]
- Im, W.; Roux, B. Ion permeation and selectivity of ompf porin: A theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 2002, 322, 851–869. [Google Scholar] [CrossRef]
- Lu, B.; Holst, M.J.; McCammon, J.A.; Zhou, Y.C. Poisson-Nernst-Planck Equations for simulating biomolecular diffusion-reaction processes I: Finite element solutions. J. Comput. Phys. 2010, 229, 6979–6994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, Q.; Chen, D.; Wei, G.-W. Second-order Poisson Nernst-Planck solver for ion channel transport. J. Comput. Phys. 2011, 230, 5239–5262. [Google Scholar] [CrossRef]
- Eisenberg, B. Multiple scales in the simulation of ion channels and proteins. J. Phys. Chem. C 2010, 114, 20719–20733. [Google Scholar] [CrossRef] [Green Version]
- Eisenberg, B. A leading role for mathematics in the study of ionic solutions. SIAM News 2012, 45, 11–12. [Google Scholar]
- Eisenberg, B. Ionic interactions are everywhere. Physiology 2013, 28, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Berti, C.; Furini, S.; Gillespie, D.; Boda, D.; Eisenberg, R.S.; Sangiorgi, E.; Fiegna, C. Three-dimensional Brownian dynamics simulator for the study of ion permeation through membrane pores. J. Chem. Theory Comput. 2014, 10, 2911–2926. [Google Scholar] [CrossRef]
- Kaufman, I.K.; McClintock, P.V.E.; Eisenberg, R.S. Coulomb blockade model of permeation and selectivity in biological ion channels. New J. Phys. 2015, 17, 083021. [Google Scholar] [CrossRef]
- Luchinsky, D.G.; Gibby, W.A.T.; Kaufman, I.K.; McClintock, P.V.E.; Timucin, D.A. Relation between selectivity and conductivity in narrow ion channels. In Proceedings of the International Conference on Noise and Fluctuations (ICNF), Vilnius, Lithuania, 20–23 June 2017; pp. 1–4. [Google Scholar]
- Catacuzzeno, L.; Franciolini, F. Simulation of gating currents of the Shaker K channel using a Brownian model of the voltage sensor. Biophys. J. 2019, 117, 2005–2019. [Google Scholar] [CrossRef] [Green Version]
- Hou, S.M.; Liu, X.-D. A numerical method for solving variable coefficient elliptic equation with interfaces. J. Comput. Phys. 2005, 202, 411–445. [Google Scholar] [CrossRef]
- Scharfetter, D.L.; Gummel, H.K. Large-signal analysis of a silicon Read diode oscillator. IEEE Trans. Elec. Dev. 1969, 16, 64–77. [Google Scholar] [CrossRef]
- Snowden, C.M. Semiconductor Device Modelling; Peter Peregrinus Ltd.: London, UK, 1988. [Google Scholar]
- Markowich, P.A.; Ringhofer, C.A.; Selberherr, S.; Lentini, M. A singular perturbation approach for the analysis of the fundamental semiconductor equations. IEEE Trans. Elec. Dev. 1983, 30, 1165–1180. [Google Scholar] [CrossRef]
- Brezzi, F.; Marini, L.D.; Pietra, P. Two-dimensional exponential fitting and applications to drift-diffusion models. SIAMJ Numer. Anal. 1989, 26, 1342–1355. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Volume II, Mainly Electromagnetism and Matter; Addison-Wesley Publishing Co.: New York, NY, USA, 1963. [Google Scholar]
- Wilczek-Vera, G.; Rodil, E.; Vera, J.H. On the activity of ions and the junction potential: Revised values for all data. AIChE J. 2004, 50, 445. [Google Scholar] [CrossRef]
- Stern, O. Zur theorie der electrolytischen doppelschicht. Z. Elektrochem. 1924, 30, 508–516. [Google Scholar]
- Oldham, K.B. A Gouy–Chapman–Stern model of the double layer at a (metal)/(ionic liquid) interface. J. Electr. Chem. 2008, 613, 131–138. [Google Scholar] [CrossRef]
- Gongadze, E.; Van Rienen, U.; Iglič, A. Generalized stern models of the electric double layer considering the spatial variation of permittvity and finite size of ions in saturation regime. Cell. Mol. Biol. Lett. 2011, 16, 576. [Google Scholar] [CrossRef]
- Brown, M.A.; Goel, A.; Abbas, Z. Effect of electrolyte concentration on the stern layer thickness at a charged interface. Angewandte Chem. Int. Ed. 2016, 55, 3790–3794. [Google Scholar] [CrossRef]
- Cole, C.D.; Frost, A.S.; Thompson, N.; Cotten, M.; Cross, T.A.; Busath, D.D. Noncontact dipole effects on channel permeation. VI. 5f- and 6F-Trp gramicidin channel currents. Biophys. J. 2002, 83, 1974–1986. [Google Scholar] [CrossRef] [Green Version]
- Gillespie, D. Energetics of divalent selectivity in a calcium channel: The ryanodine receptor case study. Biophys. J. 2008, 94, 1169–1184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, G.R.; Sansom, M.S.P. Dynamic properties of Na+ ions in models of ion channels: A molecular dynamics study. Biophys. J. 1998, 75, 2767–2782. [Google Scholar] [CrossRef] [Green Version]
- Allen, T.W.; Kuyucak, S.; Chung, S.H. Molecular dynamics estimates of ion diffusion in model hydrophobic and KcsA potassium channels. Biophys. Chem. 2000, 86, 1–14. [Google Scholar] [CrossRef]
- Mamonov, A.; Coalson, R.D.; Nitzan, A.; Kurnikova, M.G. The role of the dielectric barrier in narrow biological channels: A novel composite approach to modeling single channel currents. Biophys. J. 2003, 84, 3646–3661. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.P.; Nonner, W.; Eisenberg, R.S. PNP theory fits current-voltage (IV) relations of a neuronal anion channel in 13 solutions. Biophys. J. 1995, 68, A370. [Google Scholar]
- Nonner, W.; Eisenberg, B. Ion permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-type calcium channels. Biophys. J. 1998, 75, 1287–1305. [Google Scholar] [CrossRef] [Green Version]
- Nonner, W.; Catacuzzeno, L.; Eisenberg, B. Binding and selectivity in L-type calcium channels: A mean spherical approximation. Biophys. J. 2000, 79, 1976–1992. [Google Scholar] [CrossRef] [Green Version]
- Boda, D.; Busath, D.; Eisenberg, B.; Henderson, D.; Nonner, W. Monte Carlo simulations of ion selectivity in a biological Na+ channel: Charge-space competition. Phys. Chem. Chem. Phys. 2002, 4, 5154–5160. [Google Scholar] [CrossRef]
- Eisenberg, B. Proteins, channels, and crowded ions. Biophys. Chem. 2003, 100, 507–517. [Google Scholar] [CrossRef]
- Boda, D.; Henderson, D.; Gillespie, D. The role of solvation in the binding selectivity of the L-type calcium channel. J. Chem. Phys. 2013, 139, 055103–055110. [Google Scholar] [CrossRef]
- Boda, D. Monte Carlo simulation of electrolyte solutions in biology: In and out of equilibrium. Annu. Rev. Comput. Chem. 2014, 10, 127–164. [Google Scholar]
- Gillespie, D. A review of steric interactions of ions: Why some theories succeed and others fail to account for ion size. Microfluid. Nanofluid. 2015, 18, 717–738. [Google Scholar] [CrossRef]
- Matejczyk, B.; Valisko, M.; Wolfram, M.T.; Pietschmann, J.F.; Boda, D. Multiscale modeling of a rectifying bipolar nanopore: Comparing Poisson-Nernst-Planck to Monte Carlo. J. Chem. Phys. 2017, 146, 124125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roux, B.; Prod’hom, B.; Karplus, M. Ion transport in the gramicidin channel: Molecular dynamics study of single and double occupancy. Biophys. J. 1995, 68, 876–892. [Google Scholar] [CrossRef] [Green Version]
- Almers, W.; McCleskey, E.W. Non-selective conductance in calcium channels of frog muscle: Calcium selectivity in a single-file pore. J. Physiol. 1984, 353, 585–608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lipkind, G.M.; Fozzard, H.A. Modeling of the outer vestibule and selectivity filter of the L-type Ca2+ channel. Biochemistry 2001, 40, 6786–6794. [Google Scholar] [CrossRef]
- Cuello, L.G.; Jogini, V.; Cortes, D.M.; Perozo, E. Structural mechanism of C-type inactivation in K+ channels. Nature 2010, 466, 203–208. [Google Scholar] [CrossRef] [Green Version]
- Noskov, S.Y.; Berneche, S.; Roux, B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature 2004, 431, 830–834. [Google Scholar] [CrossRef]
- Neyton, J.; Miller, C. Discrete Ba2+ block as a probe of ion occupancy and pore structure in the high-conductance Ca2+ activated K+ channel. J. Gen. Physiol. 1988, 92, 569–596. [Google Scholar] [CrossRef] [Green Version]
- LeMasurier, M.; Heginbotham, L.; Miller, C. KcsA: It’s a potassium channel. J. Gen. Physiol. 2001, 118, 303–314. [Google Scholar] [CrossRef]
- Nimigean, C.M.; Miller, C. Na+ block and permeation in K+ channel of known structure. J. Gen. Physiol. 2002, 120, 323–325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dolinsky, T.J.; Czodrowski, P.; Li, H.; Nielsen, J.E.; Jensen, J.H.; Klebe, G.; Baker, N.A. PDB2PQR: Expanding and upgrading automated preparation of biomolecular structures for molecular simulations. Nucleic Acids Res. 2007, 35, W522–W525. [Google Scholar] [CrossRef] [PubMed]
- Lüttgau, H.-C.; Niedergerke, R. The antagonism between Ca and Na ions on the frog’s heart. J. Physiol. 1958, 143, 486–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicoll, D.A.; Longoni, S.; Philipson, K.D. Molecular cloning and functional expression of the cardiac sarcolemmal Na(+)-Ca2+ exchanger. Science 1990, 250, 562–565. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.; Li, H.; Zeng, W.; Sauer, D.B.; Belmares, R.; Jiang, Y. Structural insight into the ion-exchange mechanism of the sodium/calcium exchanger. Science 2012, 335, 686–690. [Google Scholar] [CrossRef] [PubMed]
- Blaustein, M.P.; Lederer, W.J. Sodium/calcium exchange: Its physiological implications. Physiol. Rev. 1999, 79, 763–854. [Google Scholar] [CrossRef]
- Dipolo, R.; Beaugé, L. Sodium/calcium exchanger: Influence of metabolic regulation on ion carrier interactions. Physiol. Rev. 2006, 86, 155–203. [Google Scholar] [CrossRef] [Green Version]
- Reeves, J.P.; Hale, C.C. The stoichiometry of the cardiac sodium-calcium exchange system. J. Biol. Chem. 1984, 259, 7733–7739. [Google Scholar]







| Fig.# | i | Fig.# | i | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3a | Li | 3e | Na | ||||||
| 3a | Cl | 0 | 3e | Br | |||||
| 3b | Li | 3f | K | ||||||
| 3b | Br | 3f | F | ||||||
| 3c | Na | 0 | 0 | 0 | 3g | K | |||
| 3c | F | 0 | 0 | 3g | Cl | ||||
| 3d | Na | 3h | K | ||||||
| 3d | Cl | 3h | Br | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.-L.; Eisenberg, B. Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model. Entropy 2020, 22, 550. https://doi.org/10.3390/e22050550
Liu J-L, Eisenberg B. Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model. Entropy. 2020; 22(5):550. https://doi.org/10.3390/e22050550
Chicago/Turabian StyleLiu, Jinn-Liang, and Bob Eisenberg. 2020. "Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model" Entropy 22, no. 5: 550. https://doi.org/10.3390/e22050550
APA StyleLiu, J.-L., & Eisenberg, B. (2020). Molecular Mean-Field Theory of Ionic Solutions: A Poisson-Nernst-Planck-Bikerman Model. Entropy, 22(5), 550. https://doi.org/10.3390/e22050550






