Effect of Finite-Size Heat Source’s Heat Capacity on the Efficiency of Heat Engine
Abstract
:1. Introduction
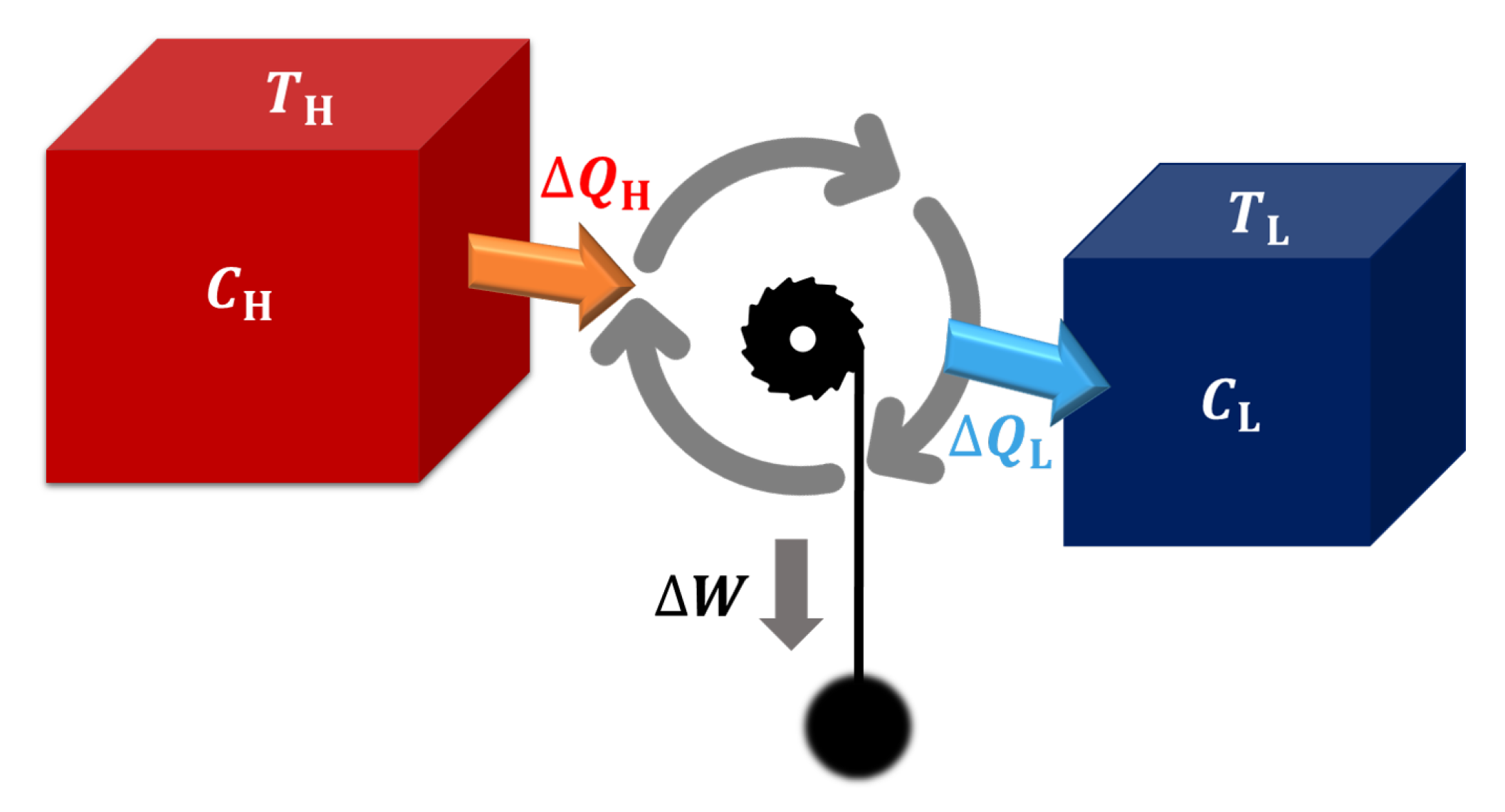
2. Heat Engine Working between Finite-Size Heat Source
2.1. High Temperature Regime
2.2. Low Temperature Regime
3. Finite-Time Performance of the Heat Engine
4. Black Holes Served as Heat Sources
5. Conclusions and Discussion
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Optimization of Low-Dissipation Carnot-Like Engine
Appendix B. Bounds for Efficiency in Finite Time in the Limit of
References
- Huang, K. Introduction To Statistical Physics, 2nd ed.; T&F/CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Tolman, R.C.; Fine, P.C. On the irreversible production of entropy. Rev. Mod. Phys. 1948, 20, 51. [Google Scholar] [CrossRef] [Green Version]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef] [Green Version]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef] [Green Version]
- Kosloff, R.; Levy, A. Quantum heat engines and refrigerators: Continuous devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef] [Green Version]
- Pekola, J.P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 2015, 11, 118–123. [Google Scholar] [CrossRef] [Green Version]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef] [Green Version]
- Binder, F.; Correa, L.A.; Gogolin, C.; Anders, J.; Adesso, G. (Eds.) Thermodynamics in the Quantum Regime; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Kosloff, R. Quantum thermodynamics and open-systems modeling. J. Chem. Phys. 2019, 150, 204105. [Google Scholar] [CrossRef]
- Scovil, H.; Schulz-DuBois, E. Three-level masers as heat engines. Phys. Rev. Lett. 1959, 2, 262. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A Math. Gen. 1979, 12, L103. [Google Scholar] [CrossRef]
- Kosloff, R. A quantum mechanical open system as a model of a heat engine. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Liu, Y.X.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brantut, J.P.; Grenier, C.; Meineke, J.; Stadler, D.; Krinner, S.; Kollath, C.; Esslinger, T.; Georges, A. A Thermoelectric Heat Engine with Ultracold Atoms. Science 2013, 342, 713–715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dechant, A.; Kiesel, N.; Lutz, E. All-Optical Nanomechanical Heat Engine. Phys. Rev. Lett. 2015, 114, 183602. [Google Scholar] [CrossRef] [Green Version]
- Rossnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325–329. [Google Scholar] [CrossRef] [Green Version]
- Abah, O.; Lutz, E. Performance of shortcut-to-adiabaticity quantum engines. Phys. Rev. E 2018, 98, 032121. [Google Scholar] [CrossRef] [Green Version]
- Passos, M.; Santos, A.C.; Sarandy, M.S.; Huguenin, J. Optical simulation of a quantum thermal machine. Phys. Rev. A 2019, 100, 022113. [Google Scholar] [CrossRef] [Green Version]
- Fialko, O.; Hallwood, D.W. Isolated Quantum Heat Engine. Phys. Rev. Lett. 2012, 108, 085303. [Google Scholar] [CrossRef]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef]
- Ma, Y.H.; Su, S.H.; Sun, C.P. Quantum thermodynamic cycle with quantum phase transition. Phys. Rev. E 2017, 96, 022143. [Google Scholar] [CrossRef] [Green Version]
- Brandner, K.; Bauer, M.; Seifert, U. Universal Coherence-Induced Power Losses of Quantum Heat Engines in Linear Response. Phys. Rev. Lett. 2017, 119, 170602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, S.; Chen, J.; Ma, Y.; Chen, J.; Sun, C. The heat and work of quantum thermodynamic processes with quantum coherence. Chin. Phys. B 2018, 27, 060502. [Google Scholar] [CrossRef] [Green Version]
- Dorfman, K.E.; Xu, D.; Cao, J. Efficiency at maximum power of a laser quantum heat engine enhanced by noise-induced coherence. Phys. Rev. E 2018, 97, 042120. [Google Scholar] [CrossRef] [Green Version]
- Camati, P.A.; Santos, J.F.G.; Serra, R.M. Coherence effects in the performance of the quantum Otto heat engine. Phys. Rev. A 2019, 99, 062103. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.F.; Sun, C.P.; Dong, H. Boosting the performance of quantum Otto heat engines. Phys. Rev. E 2019, 100, 032144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Andresen, B. Finite-Time Thermodynamics; University of Copenhagen Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Andresen, B.; Berry, R.S.; Ondrechen, M.J.; Salamon, P. Thermodynamics for processes in finite time. Acc. Chem. Res. 1984, 17, 266–271. [Google Scholar] [CrossRef]
- Wu, C. Recent Advances in Finite-Time Thermodynamics; Nova Publishers: Hauppauge, NY, USA, 1999. [Google Scholar]
- Tu, Z.C. Recent advance on the efficiency at maximum power of heat engines. Chin. Phys. B 2012, 21, 020513. [Google Scholar] [CrossRef]
- Holubec, V.; Ryabov, A. Diverging, but negligible power at Carnot efficiency: Theory and experiment. Phys. Rev. E 2017, 96, 062107. [Google Scholar] [CrossRef] [Green Version]
- Yvon, J. The Saclay Reactor: Two Years of Experience in the Use of a Compressed Gas as a Heat Transfer Agent. In Proceedings of the First Geneva Conf. Proc. UN, Geneva, Switzerland, 8–20 August 1955. [Google Scholar]
- Novikov, I. The efficiency of atomic power stations (a review). J. Nuclear Energy (1954) 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Andresen, B.; Berry, R.S.; Nitzan, A.; Salamon, P. Thermodynamics in finite time. I. The step-Carnot cycle. Phys. Rev. A 1977, 15, 2086–2093. [Google Scholar] [CrossRef]
- Chen, J. The maximum power output and maximum efficiency of an irreversible Carnot heat engine. J. Phys. D Appl. Phys. 1994, 27, 1144. [Google Scholar] [CrossRef]
- Sekimoto, K.; Sasa, S.I. Complementarity Relation for Irreversible Process Derived from Stochastic Energetics. J. Phys. Soc. Jpn. 1997, 66, 3326–3328. [Google Scholar] [CrossRef] [Green Version]
- den Broeck, C.V. Thermodynamic Efficiency at Maximum Power. Phys. Rev. Lett. 2005, 95, 190602. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Kawai, R.; Lindenberg, K.; den Broeck, C.V. Efficiency at Maximum Power of Low-Dissipation Carnot Engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.C. Efficiency at maximum power of Feynman’s ratchet as a heat engine. J. Phys. A Math. Theor. 2008, 41, 312003. [Google Scholar] [CrossRef] [Green Version]
- Holubec, V.; Ryabov, A. Maximum efficiency of low-dissipation heat engines at arbitrary power. J. Stat. Mech. Theory Exp. 2016, 2016, 073204. [Google Scholar] [CrossRef] [Green Version]
- Shiraishi, N.; Saito, K.; Tasaki, H. Universal Trade-Off Relation between Power and Efficiency for Heat Engines. Phys. Rev. Lett. 2016, 117, 190601. [Google Scholar] [CrossRef]
- Cavina, V.; Mari, A.; Giovannetti, V. Slow Dynamics and Thermodynamics of Open Quantum Systems. Phys. Rev. Lett. 2017, 119, 050601. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.H.; Xu, D.; Dong, H.; Sun, C.P. Universal constraint for efficiency and power of a low-dissipation heat engine. Phys. Rev. E 2018, 98, 042112. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.H.; Xu, D.; Dong, H.; Sun, C.P. Optimal operating protocol to achieve efficiency at maximum power of heat engines. Phys. Rev. E 2018, 98, 022133. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.H.; Zhai, R.X.; Sun, C.P.; Dong, H. Experimental validation of the 1/τ -scaling entropy generation in finite-time thermodynamics with dry air. arXiv 2019, arXiv:1910.13434. [Google Scholar]
- Ondrechen, M.J.; Andresen, B.; Mozurkewich, M.; Berry, R.S. Maximum work from a finite reservoir by sequential Carnot cycles. Am. J. Phys. 1981, 49, 681–685. [Google Scholar] [CrossRef] [Green Version]
- Ondrechen, M.J.; Rubin, M.H.; Band, Y.B. The generalized Carnot cycle: A working fluid operating in finite time between finite heat sources and sinks. J. Chem. Phys. 1983, 78, 4721–4727. [Google Scholar] [CrossRef]
- Leff, H.S. Available work from a finite source and sink: How effective is a Maxwell’s demon? Am. J. Phys. 1987, 55, 701–705. [Google Scholar] [CrossRef]
- Izumida, Y.; Okuda, K. Work output and efficiency at maximum power of linear irreversible heat engines operating with a finite-sized heat source. Phys. Rev. Lett. 2014, 112, 180603. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y. Optimization in finite-reservoir finite-time thermodynamics. Phys. Rev. E 2014, 90, 062140. [Google Scholar] [CrossRef]
- Johal, R.S. Optimal performance of heat engines with a finite source or sink and inequalities between means. Phys. Rev. E 2016, 94, 012123. [Google Scholar] [CrossRef] [Green Version]
- Johal, R.S.; Rai, R. Near-equilibrium universality and bounds on efficiency in quasi-static regime with finite source and sink. EPL (Europhys. Lett.) 2016, 113, 10006. [Google Scholar] [CrossRef] [Green Version]
- Tajima, H.; Hayashi, M. Finite-size effect on optimal efficiency of heat engines. Phys. Rev. E 2017, 96, 012128. [Google Scholar] [CrossRef] [Green Version]
- Sparaciari, C.; Oppenheim, J.; Fritz, T. Resource theory for work and heat. Phys. Rev. A 2017, 96, 052112. [Google Scholar] [CrossRef] [Green Version]
- Richens, J.G.; Alhambra, Á.M.; Masanes, L. Finite-bath corrections to the second law of thermodynamics. Phys. Rev. E 2018, 97, 062132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pozas-Kerstjens, A.; Brown, E.G.; Hovhannisyan, K.V. A quantum Otto engine with finite heat baths: Energy, correlations, and degradation. New J. Phys. 2018, 20, 043034. [Google Scholar] [CrossRef] [Green Version]
- Mohammady, M.H.; Romito, A. Efficiency of a cyclic quantum heat engine with finite-size baths. arXiv 2019, arXiv:1902.09378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barra, F. Dissipative charging of a quantum battery. Phys. Rev. Lett. 2019, 122, 210601. [Google Scholar] [CrossRef] [Green Version]
- Leff, H.S. Thermal efficiency at maximum work output: New results for old heat engines. Am. J. Phys. 1987, 55, 602–610. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1976; Volume 8. [Google Scholar]
- Esposito, M.; Lindenberg, K.; Van den Broeck, C. Universality of efficiency at maximum power. Phys. Rev. Lett. 2009, 102, 130602. [Google Scholar] [CrossRef] [Green Version]
- Pathria, R.; Beale, P. Statistical Mechanics, 3rd ed.; Academic Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Salamon, P.; Nitzan, A.; Andresen, B.; Berry, R.S. Minimum entropy production and the optimization of heat engines. Phys. Rev. A 1980, 21, 2115–2129. [Google Scholar] [CrossRef]
- Martínez, I.A.; Roldán, É.; Dinis, L.; Petrov, D.; Parrondo, J.M.R.; Rica, R.A. Brownian Carnot engine. Nat. Phys. 2015, 12, 67–70. [Google Scholar] [CrossRef]
- Taylor, E.F.; Wheeler, J.A. Exploring black holes: Introduction to general relativity, 2nd ed.; Addison-Wesley: San Francisco, CA, USA, 1975. [Google Scholar]
- Bekenstein, J.D. Black-hole thermodynamics. Phys. Today 1980, 33, 24–31. [Google Scholar] [CrossRef]
- Opatrnỳ, T.; Richterek, L. Black hole heat engine. Am. J. Phys. 2012, 80, 66–71. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Cai, Q.Y.; You, L.; Zhan, M.S. Hidden messenger revealed in Hawking radiation: A resolution to the paradox of black hole information loss. Phys. Lett. B 2009, 675, 98–101. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.H.; Cai, Q.Y.; Dong, H.; Sun, C.P. Non-thermal radiation of black holes off canonical typicality. EPL (Europhys. Lett.) 2018, 122, 30001. [Google Scholar] [CrossRef]
- Ma, Y.H.; Chen, J.F.; Sun, C.P. Dark information of black hole radiation raised by dark energy. Nucl. Phys. B 2018, 931, 418–436. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Johnson, C.V. Holographic heat engines. Class. Quantum Gravity 2014, 31, 205002. [Google Scholar] [CrossRef] [Green Version]
- Hendi, S.; Panah, B.E.; Panahiyan, S.; Liu, H.; Meng, X.H. Black holes in massive gravity as heat engines. Phys. Lett. B 2018, 781, 40–47. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Charged AdS black hole heat engines. Nucl. Phys. B 2019, 946, 114700. [Google Scholar] [CrossRef]
- d’Agostino, M.; Gulminelli, F.; Chomaz, P.; Bruno, M.; Cannata, F.; Bougault, R.; Gramegna, F.; Iori, I.; Le Neindre, N.; Margagliotti, G.; et al. Negative heat capacity in the critical region of nuclear fragmentation: An experimental evidence of the liquid-gas phase transition. Phys. Lett. B 2000, 473, 219–225. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, M.; Kusche, R.; Hippler, T.; Donges, J.; Kronmüller, W.; Von Issendorff, B.; Haberland, H. Negative heat capacity for a cluster of 147 sodium atoms. Phys. Rev. Lett. 2001, 86, 1191. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Nava, J.A.; Garzón, I.L.; Michaelian, K. Negative heat capacity of sodium clusters. Phys. Rev. B 2003, 67, 165401. [Google Scholar] [CrossRef] [Green Version]
- Campisi, M.; Fazio, R. The power of a critical heat engine. Nat. Commun. 2016, 7, 11895. [Google Scholar] [CrossRef] [PubMed]
- Abiuso, P.; Perarnau-Llobet, M. Optimal cycles for low-dissipation heat engines. arXiv 2019, arXiv:1907.02939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reitlinger, H.B. Sur l’Utilisation De La Chaleur Dans Les Machines a Feu; Vaillant-Carmanne; Beranger: Paris, France; Liege, Belgium, 1929. [Google Scholar]
- Chambadal, P. Recuperation de Chaleura la Sortie d’ un Reacteur. Les Cent. Nucl. 1957, Chapter 3. 39–58. [Google Scholar]
- Vaudrey, A.; Lanzetta, F.; Feidt, M. HB Reitlinger and the origins of the efficiency at maximum power formula for heat engines. J. Non-Equilib. Thermodyn. 2014, 39, 199–203. [Google Scholar] [CrossRef] [Green Version]
- Moreau, M.; Pomeau, Y. Carnot principle and its generalizations: A very short story of a long journey. Eur. Phys. J. Spec. Top. 2015, 224, 769–780. [Google Scholar] [CrossRef]





© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.-H. Effect of Finite-Size Heat Source’s Heat Capacity on the Efficiency of Heat Engine. Entropy 2020, 22, 1002. https://doi.org/10.3390/e22091002
Ma Y-H. Effect of Finite-Size Heat Source’s Heat Capacity on the Efficiency of Heat Engine. Entropy. 2020; 22(9):1002. https://doi.org/10.3390/e22091002
Chicago/Turabian StyleMa, Yu-Han. 2020. "Effect of Finite-Size Heat Source’s Heat Capacity on the Efficiency of Heat Engine" Entropy 22, no. 9: 1002. https://doi.org/10.3390/e22091002




