1. Introduction
Hash functions can be used in various applications such as Message Authentication, Digital Signature, Data Integrity, and Authenticated Encryption [
1]. As a definition, a hash function
H takes an input message
M, and produces an output value
h, named hash code, digital fingerprint, message digest, or simply hash. Precisely, the hash function
H takes a bit sequence
M (e.g., data, image, video, and file) with an arbitrary finite length, and produces a fixed length digest
h of
u bits. The digest acts as a kind of signature for the input data. Moreover, when the same hash function
H is run for the same input message
M, the same hash value
h is obtained [
2].
A cryptographic hash function employs an encryption algorithm in producing the output value
h. The advantage of cryptographic hash functions is to meet some security requirements and to be immune against different attacks such as statistical, brute-force, and cryptanalytic attacks, etc. Recently, CNN based hash functions [
3,
4] attract the interest of research community because of the important properties of chaotic systems and neural networks related to the nonlinear security [
5,
6].
In general, chaos is a kind of deterministic random-like process generated by nonlinear dynamical systems. Chaos was given by Edward Lorenz [
7], and its main properties have been investigated by a large community of research [
8]. Chaotic systems are appropriate to be used in cryptographic hash algorithms due to their pertinent properties such as random-like behavior, sensitivity to tiny changes in initial conditions, and unstable periodic orbits. In addition, neural networks are powerful computational models, designed to simulate the human brain and adopted to solve many problems in different fields. Neural networks exhibit, by construction, many convenient properties to be used in cryptographic hash algorithms such as parallel implementation, flexibility, nonlinearity, one-way, data diffusion, and compression functions.
At first, some designers combine both these systems (chaos and neural network) in the
Merkle–Dmgard structure to build robust CNN hash functions [
9,
10]. In our previous work [
2], Abdoun et al. designed, implemented, and analyzed the performance, in terms of security and speed, of two proposed keyed CNN hash functions based on the
Merkle–Dmgard (MD) construction with three output schemes, i.e., CNN–Matyas–Meyer–Oseas, Modified CNN–Matyas–Meyer–Oseas, and CNN–Miyaguchi–Preneel. However, the
Merkle–Dmgard construction has several vulnerabilities to some attacks such as Second preimage, Multicollisions, Herding, and Length extension attacks [
11,
12]. To resist these attacks, a new Secure Hash Algorithm called
SHA-3 [
13] based on an instance of the
KECCAK algorithm was selected as a winner of the National Institute of Standards and Technology (
NIST) hash function competition in 2015 [
13,
14,
15,
16,
17,
18]. Indeed, the
SHA-3 family consists of four cryptographic hash functions such as,
SHA3-224,
SHA3-256,
SHA3-384, and
SHA3-512 and two Extendable-Output Functions (XOFs) such as
SHAKE128 and
SHAKE256 [
13]. For the XOFs, the length of the output can be chosen to meet the requirements of user applications. There are different structures being used to build various hash functions such as
Wide Pipe [
19],
Merkle–Dmgard [
20,
21],
Haifa [
22],
Fast Wide Pipe [
23],
Sponge [
24], etc. Indeed, a number of these existing structures are employed in the design of many popular hash functions. The
Merkle–Dmgard construction is used in the design of
MD5 [
25] family like
SHA-1 [
26], and
SHA-2 [
27] standards, while the
Sponge construction is used to design a new secured standard hash algorithm
SHA-3 [
13], which will be used when the current standard
SHA-2 will be inevitably compromised. In our previous work [
28], Abdoun et al. proposed, implemented, and analyzed the performance of a new structure for keyed hash function based on chaotic maps, neural network, and
Sponge construction.
Since 2009, there are several lightweight cryptographic hash functions [
29] proposed that are based on a
Sponge construction such as
LightMAC [
30],
TuLP [
31],
SipHash [
32],
QUARK [
33],
PHOTON [
34], and
SPONGENT [
35].
In this paper, two robust keyed hash functions that contain a chaotic system (
CS) and a CNN-based
Sponge construction are proposed. In these two proposed structures, the input message
M is hashed to a hash value
h with a fixed length of bits equal to 256 or 512 bits. The combination of
Sponge construction and
CNN results the increase in the robustness of the proposed hash function. The proposed structures are based on the efficient CS [
36]. The efficient CS in [
36] produces pseudo-chaotic samples and those are used as the parameter values of the neural network. In addition, the proposed activation function of neural network is formed of two chaotic maps that are connected in parallel. The proposed CNN and CS ensure that our hash functions are more secure against different attacks in comparison with other hash functions that are based on
Sponge construction. Indeed, the various experimental results and theoretical analysis demonstrate the effectiveness and prove that the proposed hash functions have very good statistical properties, high message sensitivity, high key sensitivity, strong collision resistance, and are immune against collision, preimage, and second preimage attacks [
37].
The rest of the paper is organized as follows:
Section 2 introduces a brief reminder of cryptographic hash function properties. Then, the general models of
Sponge and
keyed-Sponge constructions are presented.
Section 3 describes in detail the proposed structures of the two keyed
CNN hash functions based on
Sponge construction with their important constitutive elements.
Section 4 shows the results and analysis in terms of security and computational performance for the proposed hash functions, and comparison with the two standards
SHA-2 and
SHA-3. Finally, in
Section 5, conclusions for the contribution and the future work are given.
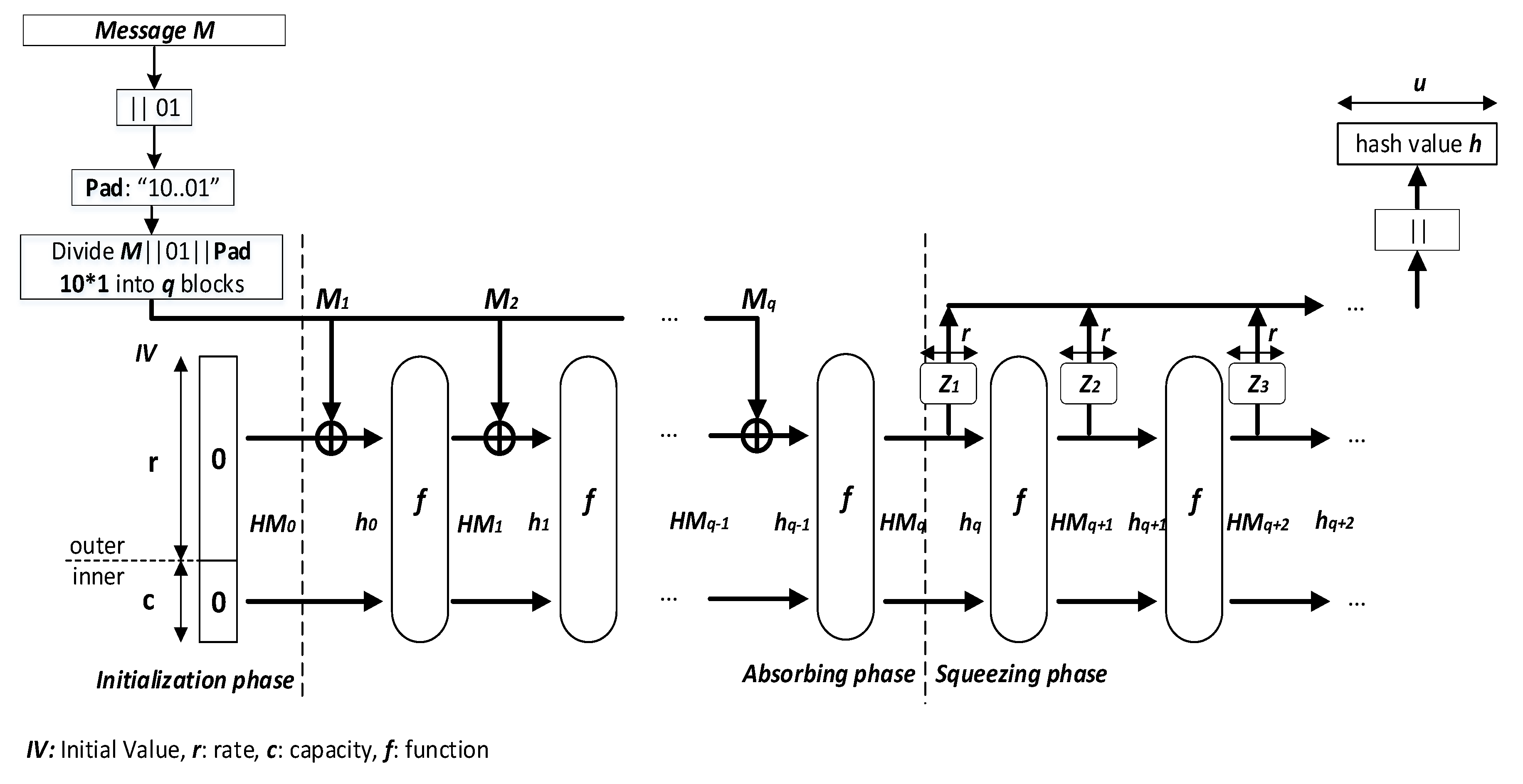
3. Proposed Keyed-Sponge Chaotic Neural Network Hash Functions
The proposed
keyed-Sponge hash functions are the chaotic functions
that contain a
CS and a
CNN [
47]. These chaotic functions use a padded message block
of size
b-bit, subkeys
of length 128 bits and a secret key
of length
= 160 bits and produce hash values with two variant lengths, 256 bits and 512 bits, depending on the value of
r and
c as shown in
Figure 3.
The first
CNN hash function is made up of a two-layered Neural Network called Structure 1, whereas the second hash function is made up of a one-layered Neural Network followed by a combination of Nonlinear (
NL) functions called Structure 2 [
28].
In the following subsection, the architecture of the two proposed keyed-Sponge CNN hash functions is described.
3.1. Description of the General Structure of the Two Proposed Keyed-Sponge CNN Hash Functions
The general structure of the proposed
keyed-Sponge CNN hash functions (
KSCNN[
c](
,
u)) is composed of three phases, i.e., Initialization, Absorbing, and Squeezing phases (see
Figure 3).
3.1.1. Phase 1: Initialization
This phase initializes the secret key
and the initial value
to 0, and determines the values of
r and
c according to
Table 1. In addition, the input message
M is appended by the suffix 01, in this phase. Then, the appended message
is padded using the function
Pad (explained below), and divided into
q blocks of the
r-bit size,
with
.
For Structures 1 and 2, we adopt the same value of c like the standard SHA-3, i.e., c equal to 512 bits (like SHA3-256) for the 256-bit hash value, and c equal to 1024 bits (like SHA3-512) for the 512-bit hash value.
We use the multi-rate padding
Pad in our proposed hash functions, which appends a bit sequence
of length
v + 2 bits (a bit 1 followed by the minimum number
v of bits 0, and lastly a bit 1), as shown in Equation (
5):
where
mod is the modulo function and
. In general, we have three cases of padding as shown in
Figure 4:
Now, let’s take a look at the three cases of padding, where
r = 1088 bits as follows:
Then, we divide the padded message into
q blocks, and the obtained message is processed as a sequence of blocks:
3.1.2. Phase 2: Absorbing
In the second phase, the
q blocks of the message,
, are absorbed, and each block is of
r bits. Each message block
,
, is padded by the sequence
. Then, the obtained blocks
with the length of
b bits are xored with the intermediate hash values
,
. It is noted that
is defined in the initialization phase (
). The obtained values from the xor operation
,
, with the length of 1600 bits form the inputs of chaotic functions
, in addition to the subkeys
,
, of 128 bits. For every
r-bit input message block
,
, the chaining variables
,
, of
b bits (e.g.,
b = 1600 bits) are filled from the outputs of
.
is the secret key of 160 bits for the first chaotic function
[
48]. For the other chaotic functions
, the subkeys
are obtained from the Least Significant Bit (
LSB) of
, or
,
. These subkeys
are used by the
CS to generate initial conditions and the necessary parameters for the
CNN. For the final chaotic function
,
forms the final hash value
with the length equal to
b bits as the output of the absorbing phase of the message
M. The pseudo-code of the absorbing phase Algorithm 1 is presented below:
| Algorithm 1 The absorbing phase. |
Require: for i = 1 to q do end for Return.
|
3.1.3. Phase 3: Squeezing
Squeezing phase is only used when the length of the hash value
u is greater than the width
b, i.e.,
. In this case, the hash value
of
b bits generated by the absorbing phase is the input to the squeezing phase, and the obtained hash values
, (
), are sequentially forwarded to
. For each
, we extract the
r most significant bits to form
, and the 128 least significant bits to produce the key
, for the
CS of each
. Finally, the
r-bit size of all obtained values
, are concatenated to constitute the final hash value
h of the desired length of
u bits as follows:
The obtained hash value
h can be used as a Message Authentication Code (
MAC) for Digital Signature (
DS) and Authenticated Encryption (
AE) applications [
49,
50]. The pseudo-code of the squeezing phase Algorithm 2 is given below:
| Algorithm 2 The squeezing phase. |
|
In the next paragraph, the proposed CS will be used in the chaotic functions , to generate the necessary parameters and initial conditions for CNN as described above.
3.2. Detailed Description of the Proposed Chaotic System
As shown in
Figure 5, the proposed
CS is a simple version of that given by
S. El Assad and
H. Noura [
36]. It is based on the Discrete Skew Tent map (
DSTmap) in Equation (
8) as
where
N is the finite precision equal to 32 bits; and
Q1 is the control parameter of
DSTmap.
KSs(
n − 1) and
KSs(n) are the outputs of
DSTmap at the
and
iterations, respectively. The value range of
Q1,
KSs(
n − 1), and
KSs(n) is from 1 to
. The secret key
K of the first input block message,
, is represented by the following equation:
where
,
,
,
, and
are parts of the secret key
K.
is only used for generation of the first sample. The components of the secret key
K are samples of 32 bits, and its size is:
3.3. Keyed-Sponge Hash Functions Based on Two-Layered CNN Structure (Structure 1)
The structure of the chaotic function
for
KSCNN[512] and
KSCNN[1024] is shown in
Figure 6. It contains two layers of neurons, i.e., a
CNN input layer of five neurons and a
CNN output layer of eight neurons. The necessary samples, Key Stream
KS, are generated by the
CS to supply the both layers. The
KS is composed as follows:
The size of
must be:
where
= 5 samples,
= 50 samples, = 10 samples, = 8 samples,
= 40
samples and
= 16 samples. Each component has 32 bits in length.
Indeed, all neurons of the two
CNN layers use the same activation function with different number of inputs. For the input layer, each neuron has 10 inputs receiving data from
as displayed in
Figure 6 and
Figure 7. In addition, for
, the first five inputs
,
, of each neuron are weighted by the
,
, and then added together with the bias
(weighted by 1), to form the input of the chaotic map
DSTmap. The last five inputs
, are weighted by
, and then combined together with the same bias
to form the input of the chaotic map
DPWLCmap. All inputs
, biases
and weights
are samples (integer values) of 32 bits.
and
are the control parameters of
DSTmap and
DPWLCmap, respectively. The biases
,
, are necessary in case the input message is null as seen in
Figure 7. The chaotic map
DPWLCmap is realized as follows:
where
KSp(
n − 1) and
KSp(n) are the outputs of
DPWLCmap at the
and
iterations, respectively;
N is the number of bits defining the finite precision,
bits;
Q2 is the control parameter;
KSp(
n − 1),
KSp(n) and
Q2 range between 1 to
.
After computation, the two outputs of
DSTmap and
DPWLCmap are xored together to produce the output of neurons represented by
,
, which is presented by the following equation:
At the output layer, each neuron has five inputs,
, where
k represents the index of output neurons,
j represents the index of input neurons;
,
, are the weights associated with the connections between output and input layers, and
,
are the outputs of neurons at the input layer;
,
, and
,
, both are samples of 32-bit length. As presented in
Figure 8 for the inputs of each neuron at the output layer, the outputs of the first three neurons at the input layer,
,
and
, are fed to the chaotic map
DSTmap, and the last two outputs
and
from the input layer are sent to the chaotic map
DPWLCmap. After computation, the outputs of chaotic maps
DSTmap and
DPWLCmap are xored together to generate the output of the neuron, given by the following equation:
Here, the control parameters , , , and the biases , , used by the two chaotic maps, are also samples of 32 bits in length.
Finally, the output layer of the proposed structure is iterated seven times to produce the intermediate hash values with the length b = bits.
3.4. Keyed-Sponge Hash Functions Based on One-Layered CNN and One NL Output Layer (Structure 2)
The architecture of the second proposed
KSCNN hash function uses the same input
CNN layer as that in Structure 1, and the second layer is replaced by
NL functions. The
NL functions are similarly used in
SHA-2 as displayed in
Figure 9. The
CS generates the necessary samples to supply the
CNN of each
,
as
and its size is
Here, = 5 samples instead of 40 samples as used in Structure 1.
The outputs of neurons at the input layer
,
are calculated by Equation (
14). As seen in
Figure 10, the outputs of neurons are weighted by
,
, to form the inputs
for the
NL functions of the output layer;
. The outputs
are calculated by the following equations:
where
,
are values of 32-bit length and
,
are truncated to 32 bits. The four
NL functions,
Maj,
Ch,
and
, are defined by the equations as
where the denotations are ¬: NOT logic, ∧: AND logic, ∨: OR logic, ⊕: XOR logic, ≪: binary shift left operation, and ≫: binary shift right operation.
To compute the intermediate hash values, the output layer is iterated times firstly, while the value of (1, 2, 4, 8, 16, and 24) depends on the desired security level. The obtained results given in the performance section indicate that = 8 rounds is sufficient. Then, with fixed , we again iterate the output layer seven times to obtain the desired length of the intermediate hash values as done in Structure 1.
4. Performance Analysis
In order to evaluate the performance of
KSCNN[512] and
KSCNN[1024], the performance analysis focuses on the security and the number of needed cycles per byte (
NCpB). In addition, we compare the obtained performance with the standard hash algorithm
SHA-3. First, we analyze the preimage resistance (one-way property) of the proposed structures. Then, we evaluate the statistical tests such as the collision resistance, the distribution of hash value, the sensitivity of hash value
h to the message
M and the sensitivity of hash value
h to the secret key
K, and the diffusion effect. In addition, we study the immunity of the proposed structures against the brute-force and cryptanalytic attacks. The detailed description of these tests is presented in our previous work [
47]. For that, we just resume in this section the necessary test description to interpret the obtained results.
4.1. One-Way Property
According to Equations (
14) and (
15), for a hash value
h, it is highly difficult to retrieve the secret key
K and the message
M. For a given secret key
K, the attacker tries to find the message
M using the brute force attack (as explained in the
Section 4.3.1), such that its hash is equal to a given hash value. On average, an attacker tries
values of the message, to find the hash value
h of length
u (
u is equal to 256 or 512 bits). Nowadays, with such lengths, this attack is infeasible [
51,
52].
4.2. Statistical Tests
In this sub-section, we implement and analyze the different statistical tests.
4.2.1. Collision Resistance Analysis
This statistical test quantitatively evaluates the collision resistance [
51]. For that, given a hash value
h of a random message
M in the ASCII format
, and its corresponding
obtained with one bit flipping of the same message
M, we calculate the number of hits
as follows:
where the function
The value , and is the function that converts the entries to their equivalent decimal values.
In theory, the relation between a number of tests and a number of hits
as mentioned in [
53] that
where
J represents the number of independent experiments. These theoretical values of
according to Equation (
22) are given in
Table 2 and
Table 3 for hash values with the lengths of 256 and 512 bits, respectively.
For the two lengths of hash values, the obtained results in
Table 4 indicate that the number of rounds
= 8 and
= 24 give the best results. Indeed, for 256-bit hash value length with
= 8, there are two hits for 17 tests, one hit for 244 tests, and zero hits for 1787 tests. For
= 24, there are two hits for 11 tests, one hit for 213 tests, and zero hits for 1824 tests. Similar behavior is obtained for the 512-bit hash value with a slight increase in the number of hits.
In
Table 5, we summarize the obtained number of hits
for the two proposed structures. As expected, we obtain comparable results. The absolute difference
d of two hash values is calculated as
The mean, mean/character, minimum, and maximum of
d are presented in
Table 6. It is clear that the values of mean/character are close to the expected ones as observed from the obtained results, evaluated by Equation (
24) that are equal to 85.33 for 256-bit hash value length (
L = 256) and equal to 170.66 for 512-bit hash value length [
54]:
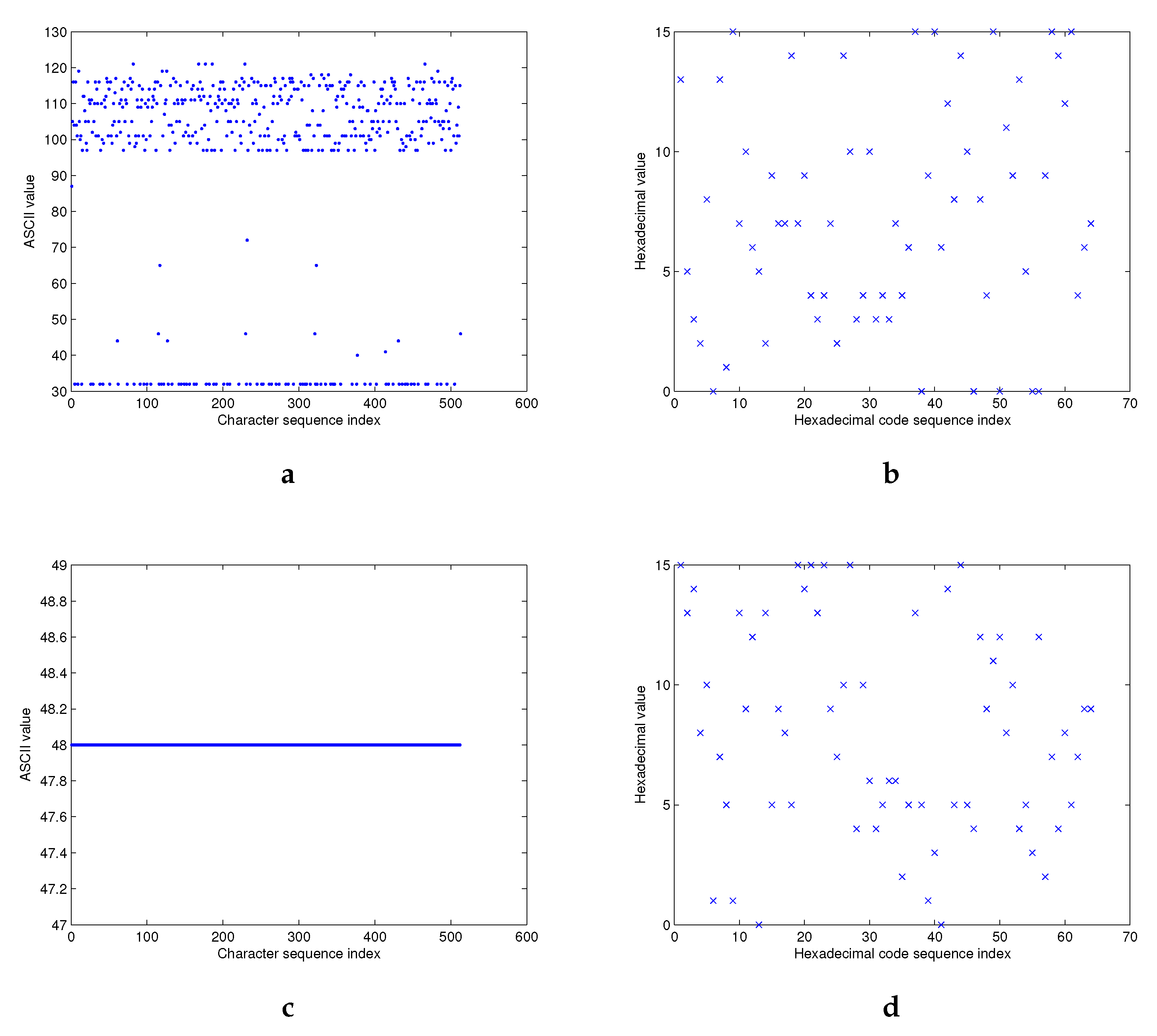
4.2.2. Hash Value Distribution
Theoretically, the hash value h, produced by a hash function H, should be uniformly distributed in the entire output range. For this purpose, we execute the following test for a given message M as:
“With the wide application of Internet and computer technique, information security becomes more and more important. As we know, hash function is one of the cores of cryptography and plays an important role in information security. Hash function takes a message as input and produces an output referred to as a hash value. A hash value serves as a compact representative image (sometimes called digital fingerprint) of input string and can be used for data integrity in conjunction with digital signature schemes.”
The hash value
h is computed using Structures 1 and 2 with the 256-bit and 512-bit hash value lengths. In
Figure 11, we exhibit the ASCII values of the message
M (
Figure 11a), and its hexadecimal hash value
h (
Figure 11b) according to their index of positions.
As predicted, the distribution of the original message is located around a small area, while the distribution of hexadecimal hash value looks like a mess. The distribution of the hash value
h (
Figure 11d) is also verified, even under the worst case of zero input message (
Figure 11c). Similar results are obtained for the two proposed structures with their two variant hash output lengths.
4.2.3. Sensitivity of Hash Value h to the Input Message M
A hash function
H is very sensitive to an input message
M. It means that a small change in its input will generate a totally different hash value
. To this end, for a given secret key
K, the hash value
in hexadecimal, the number of changed bits
, and the sensitivity of the hash value
h to the original message
M are measured by Hamming Distance
for the two proposed structures with their two variants of hash value lengths of 256 and 512 bits as
and
The different message variants are obtained under the following six conditions:
Condition 1: The input message
M is the one given in
Section 4.2.2.
Condition 2: The first character W in the input message is changed to X.
Condition 3: The word With in the input message is changed to Without.
Condition 4: The dot at the end of the input message is changed to the comma.
Condition 5: A blank space at the end of the input message is added.
Condition 6: We exchange the first block
“With the wide application of Internet and computer technique, information security becomes more and more important. As we know, hash function is one of the cores of cryptography and plays an important role in information security. Hash function takes a mes,”
with the second block
“sage as input and produces an output referred to as a hash value. A hash value serves as a compact representative image (sometimes called digital fingerprint) of input string and can be used for data integrity in conjunction with digital signature schemes.”
With each condition,
Table 7 shows the obtained results of
, and
for the 256-bit hash value. Similar results are obtained for
= 512 bits. In
Table 8, the obtained results for the two structures with their two lengths of 256 and 512 bits are compared. All the results are close to the expected values (
= 128 bits for the 256-bit hash value length,
= 256 for the 512-bit hash value length, and
= 50% for all proposed structures), demonstrating the high sensitivity to the input message
M for the two proposed structures.
4.2.4. Sensitivity of Hash Value h to the Secret Key K
A hash function H is highly sensitive to the secret key K when a slight change in K produces a completely different hash value . Here, for the previous message M with each of the five following conditions and for the two proposed structures with their two variants of hash value length 256 and 512 bits, we calculate the hash value (hexadecimal), the number of changed bits (bits), and the sensitivity of the hash value h to the secret key K measured by Hamming Distance :
Condition 1: The original secret key K is used.
In each of these conditions, we flip the LSB in the aforementioned parameters and initial conditions.
Condition 2: The initial condition KSs(0) in the secret key is changed.
Condition 3: The parameter Ks in the secret key is changed.
Condition 4: The initial condition KSs(−1) in the secret key is changed.
Condition 5: The control parameter Q1 in the secret key is changed.
Table 9 presents the obtained results of
, and
for 256-bit hash value length. Comparable results are obtained for
= 512 bits. We compare the results of the two proposed structures for two lengths of 256 and 512 bits in
Table 10. All results obtained are close to the expected values (
= 128 bits for the 256-bit hash value length,
= 256 for the 512-bit hash value length, and
= 50% for all proposed structures), demonstrating the high sensitivity to the secret key
K of the two proposed structures.
4.2.5. Statistical Analysis of the Diffusion Effect
We obtain the optimal value of diffusion effect when flipping any bit in the input message
M that causes a change of each output bit (binary format) in the hash value
h with a probability of 50% [
55]. This is often mentioned as the
Strict Avalanche Criterion (
SAC) in literature [
56].
To quantify the performance of Structures 1 and 2 with their variants of hash output lengths of 256 and 512 bits, we execute the following diffusion test.
First, the hash value h for the previous message M is generated. Next, a new hash value h’ for the same message M with one randomly changed bit is produced. Then, the number of bits changed between the two obtained hash values h and h’ is calculated. This experiment is repeated J times, with J = 512, 1024, and 2048. Finally, we compute the six following statistical tests as below:
Minimum number of bits changed:
bits
Maximum number of bits changed:
bits
Mean number of bits changed:
bits
Mean changed probability (mean of ):
%
Standard variance of the changed bit number:
Standard variance of the changed probability:
%
The obtained results given in
Table 11 with 2048 tests demonstrate that the diffusion effect is close to the expected results (
= 128 bits for the 256-bit hash value length,
= 256 for the 512-bit hash value length, and
P = 50% for all proposed structures). In addition, it is noted that the diffusion is extremely stable for whatever the hash value length
in both Structure 1 and 2 because both the mean of number of changed bits
and the mean of changed probability
P are very close to the ideal values, while
and
are very small.
For different number of tests (J = 512, 1024, and so on), similar results are obtained for the two proposed structures with their different hash value lengths (256 and 512 bits).
In addition, the histograms of
as seen in
Figure 12 and
Figure 13 of Structure 1 illustrate that the values of
are centered on the ideal values 128 and 256 bits for
u = 256 and 512 bits, respectively. We obtain similar results for Structure 2.
4.3. Cryptanalysis
In the literature, there exist known attacks, which can be applied to the two categories of hash functions, unkeyed or keyed. In [
24],
Bertoni et al. demonstrate the dependency of these known attacks on the hash value length
u for the unkeyed hash function with the secret key length
and for the keyed hash function with the hash value length
u. Normally, if an attacker comprises the secret key
K, then the system is completely compromised during the key life time [
57]. In the following, the robustness of the proposed two structures, Structures 1 and 2, against these known attacks is demonstrated.
4.3.1. Brute Force Attacks
The brute force attacks can be carried out on the secret key K (namely, exhaustive key search attack) and on the hash value h. We order the attacks on the hash value h from the easiest one to the hardest one:
Exhaustive Key Search Attack [
58]:
With this kind of attack, the attacker needs = tries for the two proposed hash functions. Thus, this attack is ineffective.
Collision Resistance Attack (Birthday Attack) [
59]:
With this kind of attack, the attacker tries to find two different messages , which the proposed hash functions produce the same hash value h. To break the collision resistance property, the smaller workload expected by the attacker is approximately equal to .
Preimage and Second Preimage Attacks [
60]:
With the Preimage attack, the attacker tries to find the original message M for a known value h such that H(M) = h. In the Second preimage attack, knowing the hash value h for a given input message M, the attacker tries to find another message that produces the same hash value h. With these two types of attacks, the smaller expected workload required by the attacker to break the collision resistance property is approximately .
In conclusion, to realize the attack on the hash value h for the two proposed structures with the minimum length (u = 256 bits), the minimum workload required by the attacker is attempts, which is infeasible.
4.3.2. Cryptanalytic Attacks
With these kinds of attacks, the attacker tries to find specific weaknesses in the structure of a hash function, and performs on it some attacks, and it is expected that the amount of effort less than that with the brute force attack. In the next paragraphs, the two most common cryptanalytic attacks in the literature against the proposed hash functions are considered such that:
In the two proposed hash functions, the secret key K is used as an input for the CS to produce the necessary supplies to the CNN, and is not prepended to the message M. Then, this type of attack cannot be conducted.
Meet-in-the-Middle Preimage Attack [
62]:
The Meet-in-the-middle (
MITM) attack is a generic cryptanalytic approach that is originally applied to the cryptographic systems based on block ciphers (chosen-plaintext attack). In 2008,
Aoki and
Sasaki [
62] noticed that the
MITM attack could be applied to hash functions, to find collision, preimage, or second preimage for intermediate hash chaining values instead of the final hash value
h. This attack has successfully broken several hash function designs. As our hash functions are preimage resistant, the minimum effort (with
u = 256 bits) to succeed the
MITM attack with probability 0.632 is
tries.
4.4. Computing and Complexity Analysis
Here, the computing performance and the computational complexity of the two proposed structures are analyzed. Firstly, the computing performance of the two proposed structures with their hash value lengths of 256 and 512 bits for different message lengths is estimated. Then, the average hashing throughput
HTH [MBytes/second] and the needed number of cycles to hash one Byte
NCpB [cycles/byte] are calculated by Equations (
27) and (
28), respectively, as
where
HT [second] is the average hashing time. The calculation is done in C code, running an Ubuntu Linux 14.04.1 (64-bit) operating system and using a computer with a 2.9 GHZ Intel core i7-4910MQ CPU and with 4 GB of RAM. In
Table 12 and
Table 13, the average
HT, the average
HTH, and the average
NCpB for the two proposed structures with their two hash value lengths of 256 and 512 bits are given. When the overhead related to the structures becomes negligible (from 10,000 data bytes and more), we observe that for any length of the hash values (256 or 512 bits), the hash throughput
HTH of Structure 2 is just over twice that compared to Structure 1. In addition, we observe that, with any proposed structure, the hash throughput
HTH with
equal to 256 bits (
r = 1088 bits and
c = 512 bits) is approximately twice the value with
equal to 512 bits (
r = 576 bits and
c = 1024 bits). Indeed, when
r is increased, the hash time
HT of the absorbing phase is decreased. Additionally, the
HTH for the two proposed structures with their different hash value lengths are shown in
Figure 14.
In addition, the computational complexity of the proposed functions varies with the number of required instructions and the latency of executions of these instructions. The computational complexity can be estimated by the big-
O notation, which excludes constants, coefficients, and lower order terms. Indeed, the complexity is represented as a function
O(
f(
n)) that depends on the input size
n. It should be noted that the complexity of a series of sentences is in the same order of the sum of the individual complexities. In addition, some practical rules are considered to calculate the complexity [
63] as
Input–output simple sentences are on the order of O(1).
If sentences are on the order of O(1).
For cycle is on the order of O(1) for k iterations independent of the input n or on the order of O(n) for n iterations.
For double nested cycle is on the order of O() for n iterations for each cycle.
Iterative cycles with divisive-multiplicative sentences are on the order of O(log n) for n iterations.
O(log n) in the For cycle with n iterations is on the order of O(n log n).
The two proposed hash functions (Structures 1 and 2) are based on Sponge construction. These proposed hash functions are built as follows:
The hashing process starts by taking a block message with fixed length as input.
The message block is padded using a cryptographically secure padding scheme.
The padded message block is entered for a combination of operations with a key obtained from the output of the previous block.
The final hash block outputs a fixed length hash value having the same size as the input block.
In our proposed hash functions, the equations of the key generator, neural network layers, and nonlinear functions are realized by multiplication/division and addition/subtraction operations. In addition,
for double nested operations are used. This means that the computational complexity of the two proposed hash functions is on the order of
O(
) [
64,
65].
4.5. Performance Comparison with the Standards SHA3, SHA2, and with Other Chaos-Based Hash Functions
This section presents the comparison of the computing performance for our proposed hash functions with the standard hash functions SHA-3, SHA-2 and some chaos-based hash functions in the literature in terms of robustness and speed. To the best of our knowledge, there has not been any chaos-based hash function using Sponge construction in the literature.
In
Table 14,
Table 15,
Table 16,
Table 17 and
Table 18, we compare the obtained statistical results (collision resistance, diffusion, and message sensitivity) of our proposed chaos-based hash functions with the standard
SHA-3 for
with the lengths of 256 and 512 bits, and with the standard
SHA-2 and some other chaos-based hash functions in the literature for
equal to 256 bits. We can conclude that, after carefully analyzing the values in these tables, all of our obtained statistical results are close to those of the standard
SHA-3 and of the other hash functions.
A comparison in terms of the needed number of cycles to hash one byte (
NCpB) of the proposed chaos-based hash functions with the standard
SHA-3 for 2048 tests and different data sizes is given in
Table 19. We observe that globally the performance of the standard hash algorithm
SHA-3 in terms of
NCpB is better than that obtained by the proposed our hash functions. For example, for the long messages with length equal to 1 MB, the
NCpB obtained by
SHA-3 for both the hash length value, is seven times less than the
NCpB of Structure 1, but it is only less than three times of the
NCpB obtained by Structure 2 with
= 8. However, we do our simulations in the sequential implementation without optimization. Thus, with a parallel implementation (with 50 output neurons at the input layer) using optimized calculation, the performance computing will be at least similar to that obtained on
SHA-3 [
66]. It can be even better than that of
SHA-3 when using our proposed Structure 2 with
= 8.
Finally, we give a comparison of
NCpB of the proposed structures with 256-bit and 512-bit hash values with some chaos-based hash functions and with the standards
SHA-2 and
SHA-3 for one Mbits data size in
Table 20. We observe that the obtained
NCpB is better than the
NCpB of the other cited works, except for that obtained in our previous work [
47]. It is because the the structure of the
Sponge construction is more complex than that of the
Merkle–Dmgard construction.
Table 14.
Comparison of collision resistance for the two proposed structures with = 256 bits with the standards SHA-3, SHA-2 and with some chaos-based hash functions.
Table 14.
Comparison of collision resistance for the two proposed structures with = 256 bits with the standards SHA-3, SHA-2 and with some chaos-based hash functions.
| Hash Function | Number of Hits | Absolute Difference d |
|---|
| | 0 | 1 | 2 | 3 | | Mean | Mean/Character | Minimum | Maximum |
|---|
| Structure 1 | 1806 | 229 | 13 | 0 | | 2715.39 | 84.85 | 1695 | 3831 |
| Structure 2 with = 8 | 1787 | 244 | 17 | 0 | | 2584.51 | 80.76 | 1654 | 3759 |
| Structure 2 with = 24 | 1824 | 213 | 11 | 0 | | 2665.24 | 83.28 | 1642 | 3784 |
| Abdoun et al. 1 [47] | 1931 | 114 | 3 | 0 | | 1291.64 | 80.72 | 480 | 2038 |
| Abdoun et al. 2- = 8 [47] | 1929 | 114 | 5 | 0 | | 1426.23 | 89.13 | 730 | 2213 |
| Abdoun et al. 2- = 24 [47] | 1942 | 106 | 0 | 0 | | 1338.85 | 83.67 | 629 | 2071 |
| SHA3-256 [13] | 1818 | 211 | 19 | 0 | | 2776.16 | 86.75 | 1686 | 3895 |
| SHA2-256 [27] | 1817 | 220 | 11 | 0 | | 2707.10 | 84.59 | 1789 | 3819 |
| Xiao et al. [51] | - | - | - | - | | 1506 | 94.12 | 696 | 2221 |
| Xiao et al. [67] | 1926 | 120 | 2 | 0 | | 1227.8 | 76.73 | 605 | 1952 |
| Deng et al. [68] | 1940 | 104 | 4 | 0 | | 1399.8 | 87.49 | 583 | 2206 |
| Yang et al. [69] | - | - | - | - | | - | 93.25 | - | - |
| Xiao et al. [70] | 1915 | 132 | 1 | 0 | | 1349.1 | 84.31 | 812 | 2034 |
| Li et al. [71] | 1901 | 146 | 1 | 0 | | 1388.9 | 86.81 | 669 | 2228 |
| Wang et al. [72] | 1917 | 126 | 5 | 0 | | 1323 | 82.70 | 663 | 2098 |
| Huang [73] | 1932 | 111 | 5 | 0 | | 1251.2 | 78.2 | 650 | 1882 |
| Li et al. [74] | 1928 | 118 | 2 | 0 | | 1432.1 | 89.51 | 687 | 2220 |
| Li et al. [3] | 1899 | 124 | 25 | 0 | | 1367.6 | 85.47 | 514 | 2221 |
| Li et al. [75] | 1920 | 124 | 4 | 0 | | 1319.5 | 82.46 | 603 | 2149 |
| He et al. [4] | 1926 | 118 | 4 | 0 | | 1504 | 94 | 683 | 2312 |
| Xiao et al. [76] | 1924 | 120 | 4 | 0 | | 1431.3 | 89.45 | 658 | 2156 |
| Yu-Ling et al. [77] | 1928 | 117 | 3 | 0 | | 1598.6 | 99.91 | 796 | 2418 |
| Xiao et al. [78] | 1932 | 114 | 2 | 0 | | 1401.1 | 87.56 | 573 | 2224 |
| Li et al. [79] | 1920 | 122 | 6 | 0 | | - | - | - | - |
| Li et al. [80] | 1905 | 135 | 8 | 0 | | 1335 | 83.41 | 577 | 2089 |
| Ahmad et al. [81] | 1923 | 121 | 4 | 0 | | 1364.7 | 85.29 | 537 | 2399 |
| Li et al. [82] | 1957 | 82 | 9 | 0 | | 1425 | 89.07 | 646 | 2096 |
| Lin et al. [83] | 1931 | 114 | 3 | 0 | | - | 90.23 | - | - |
Table 15.
Comparison of collision resistance for the two proposed structures with the standard SHA-3 for = 512 bits.
Table 15.
Comparison of collision resistance for the two proposed structures with the standard SHA-3 for = 512 bits.
| Hash Function | Number of Hits | Absolute Difference d |
|---|
| | 0 | 1 | 2 | 3 | 4 | | Mean | Mean/Character | Minimum | Maximum |
|---|
| Structure 1 | 1572 | 419 | 51 | 6 | 0 | | 5414.34 | 169.19 | 3911 | 7062 |
| Structure 2 with = 8 | 1607 | 371 | 67 | 3 | 0 | | 5478.30 | 171.19 | 3874 | 6871 |
| Structure 2 with = 24 | 1600 | 399 | 46 | 2 | 1 | | 5233.34 | 163.54 | 3767 | 6606 |
| SHA3-512 [13] | 1593 | 418 | 35 | 2 | 0 | | 5502.66 | 171.95 | 3933 | 7106 |
Table 16.
Comparison of the statistical results of diffusion effect for the two proposed structures with = 256 bits with the standards SHA-3, SHA-2 and with some chaos-based hash functions.
Table 16.
Comparison of the statistical results of diffusion effect for the two proposed structures with = 256 bits with the standards SHA-3, SHA-2 and with some chaos-based hash functions.
| Hash Function | | | | P(%) | | |
|---|
| Structure 1 | 101 | 155 | 128.10 | 50.04 | 7.96 | 3.11 |
| Structure 2 with = 8 | 99 | 156 | 127.70 | 49.88 | 8.22 | 3.21 |
| Structure 2 with = 24 | 99 | 154 | 127.88 | 49.95 | 8.02 | 3.13 |
| Abdoun et al. 1 [47] | 100 | 154 | 127.95 | 49.98 | 8.03 | 3.13 |
| Abdoun et al. 2- = 8 [47] | 103 | 157 | 127.97 | 49.99 | 8.01 | 3.13 |
| Abdoun et al. 2- = 24 [47] | 100 | 157 | 127.88 | 49.95 | 7.94 | 3.10 |
| SHA3-256 [13] | 101 | 153 | 128.05 | 50.02 | 8.01 | 3.13 |
| SHA2-256 [27] | 104 | 154 | 128.01 | 50.00 | 7.94 | 3.10 |
| Xiao et al. [51] | - | - | 63.85 | 49.88 | 5.78 | 4.52 |
| Lian et al. [52] | - | - | 63.85 | 49.88 | 5.79 | 4.52 |
| Zhang et al. [53] | 46 | 80 | 63.91 | 49.92 | 5.58 | 4.36 |
| Wang et al. [84] | - | - | 63.98 | 49.98 | 5.53 | 4.33 |
| Xiao et al. [67] | - | - | 64.01 | 50.01 | 5.72 | 4.47 |
| Deng et al. [85] | - | - | 63.91 | 49.92 | 5.58 | 4.36 |
| Deng et al. [68] | - | - | 63.84 | 49.88 | 5.88 | 4.59 |
| Yang et al. [69] | - | - | 64.14 | 50.11 | 5.55 | 4.33 |
| Xiao et al. [70] | - | - | 64.09 | 50.07 | 5.48 | 4.28 |
| Amin et al. [86] | - | - | 63.84 | 49.88 | 5.58 | 4.37 |
| Li et al. [71] | 45 | 81 | 63.88 | 49.90 | 5.37 | 4.20 |
| Wang et al. [72] | - | - | 63.90 | 49.93 | 5.64 | 4.41 |
| Akhavan et al. [87] | 42 | 83 | 63.91 | 49.92 | 5.69 | 4.45 |
| Huang [73] | - | - | 63.88 | 49.91 | 5.75 | 4.50 |
| Li et al. [74] | - | - | 63.80 | 49.84 | 5.75 | 4.49 |
| Wang et al. [88] | 44 | 82 | 64.15 | 50.11 | 5.76 | 4.50 |
| Li et al. [3] | - | - | 63.56 | 49.66 | 7.42 | 5.80 |
| Li et al. [75] | - | - | 63.97 | 49.98 | 5.84 | 4.56 |
| He et al. [4] | 45 | 83 | 64.03 | 50.02 | 5.60 | 4.40 |
| Jiteurtragool et al. [89] | 43 | 81 | 62.84 | 49.09 | 5.63 | 4.40 |
| Teh et al. [10] | - | - | 64.01 | 50.01 | 5.61 | 4.38 |
| Chenaghlu et al. [90] | - | - | 64.12 | 50.09 | 5.63 | 4.41 |
| Akhavan et al. [91] | 43 | 82 | 63.89 | 49.91 | 5.77 | 4.50 |
| Nouri et al. [92] | - | - | 64.08 | 50.06 | 5.72 | 4.72 |
| Xiao et al. [76] | 47 | 83 | 63.92 | 49.94 | 5.62 | 4.39 |
| Yu-Ling et al. [77] | - | - | 64.17 | 50.14 | 5.74 | 4.49 |
| Xiao et al. [78] | - | - | 64.18 | 50.14 | 5.59 | 4.36 |
| Li et al. [79] | - | - | 64.07 | 50.06 | 5.74 | 4.48 |
| Li et al. [80] | - | - | 63.89 | 49.91 | 5.64 | 4.41 |
| Ren et al. [93] | - | - | 63.92 | 49.94 | 5.78 | 4.52 |
| Guo et al. [94] | - | - | 63.40 | 49.53 | 7.13 | 6.35 |
| Yu et al. [95] | 45.6 | 81.8 | 63.98 | 49.98 | 5.73 | 4.47 |
| Zhang et al. [96] | - | - | 64.43 | 49.46 | 5.57 | 4.51 |
| Jiteurtragool et al. [89] | 101 | 153 | 126.75 | 49.51 | 7.98 | 3.12 |
| Chenaghlu et al. [90] | 101 | 168 | 128.08 | 50.03 | 8.12 | 3.21 |
| Teh et al. [97] | - | - | 64.00 | 50.00 | 5.44 | 4.25 |
| Li et al. [82] | 45 | 84 | 64.27 | 50.21 | 5.59 | 4.36 |
| Ahmad et al. [81] | 45 | 82 | 63.87 | 49.90 | 5.58 | 4.36 |
| Lin et al. [83] | - | - | 64.10 | 50.08 | 5.58 | 4.36 |
Table 17.
Comparison of the statistical results of diffusion effect for the proposed structures with the standard SHA-3 for = 512 bits.
Table 17.
Comparison of the statistical results of diffusion effect for the proposed structures with the standard SHA-3 for = 512 bits.
| Hash Function | | | | P (%) | | |
|---|
| Structure 1 | 217 | 293 | 256.20 | 50.04 | 11.20 | 2.18 |
| Structure 2 with = 8 | 214 | 291 | 255.90 | 49.98 | 11.37 | 2.22 |
| Structure 2 with = 24 | 215 | 296 | 255.53 | 49.90 | 11.41 | 2.23 |
| SHA3-512 [13] | 221 | 288 | 255.82 | 49.96 | 11.08 | 2.16 |
Table 18.
Comparison of average and for the sensitivity of the hash value to the message of the two proposed structures with the standard SHA-3 for equal to 256 and 512 bits.
Table 18.
Comparison of average and for the sensitivity of the hash value to the message of the two proposed structures with the standard SHA-3 for equal to 256 and 512 bits.
| | Length of Hash Values | | |
|---|
| Structure 1 | 256 | 137.60 | 53.75 |
| | 512 | 266.00 | 51.95 |
| Structure 2 | 256 | 128.00 | 50.00 |
| = 8 | 512 | 204.40 | 39.92 |
| Structure 2 | 256 | 134.60 | 52.57 |
| = 24 | 512 | 254.20 | 49.64 |
| SHA-3 [13] | 256 | 124.00 | 48.43 |
| | 512 | 248.00 | 48.43 |
Table 19.
Comparison of NCpB of the two proposed structures with the standard SHA-3 for equal to 256 and 512 bits.
Table 19.
Comparison of NCpB of the two proposed structures with the standard SHA-3 for equal to 256 and 512 bits.
| Message Length | Structure 1 | Structure 2 with = 8 | Structure 2 with = 24 | SHA-3 |
|---|
| | 256 | 512 | 256 | 512 | 256 | 512 | 256 | 512 |
|---|
| 513 | 124.33 | 172.47 | 30.24 | 54.61 | 28.20 | 75.04 | 13.53 | 59.39 |
| 1024 | 60.68 | 103.42 | 24.45 | 57.64 | 51.78 | 78.30 | 32.12 | 48.83 |
| 2048 | 93.56 | 107.66 | 24.43 | 42.32 | 27.08 | 57.99 | 27.10 | 41.22 |
| 4096 | 53.28 | 98.48 | 33.38 | 55.19 | 35.27 | 54.32 | 15.92 | 13.82 |
| 63.51 | 101.87 | 22.44 | 42.49 | 30.71 | 47.82 | 13.28 | 13.43 |
| 50.30 | 93.67 | 21.21 | 40.12 | 24.56 | 46.16 | 6.92 | 12.95 |
Table 20.
Comparison of NCpB of Structures 1 and 2 with 256-bit and 512-bit hash values length with the standards SHA-3 and SHA-2 and with some chaos-based hash functions and.
Table 20.
Comparison of NCpB of Structures 1 and 2 with 256-bit and 512-bit hash values length with the standards SHA-3 and SHA-2 and with some chaos-based hash functions and.
| Hash Function | Structure 1 | Structure 2 with = 8 | Structure 2 with = 24 | SHA-3 | SHA-2 |
|---|
| | 256 | 512 | 256 | 512 | 256 | 512 | 256 | 512 | 256 | 512 |
|---|
| NCpB | 50.30 | 93.67 | 21.21 | 40.12 | 24.56 | 46.16 | 6.92 | 12.95 | 11.87 | 13.72 |
| Hash function | 1 [47] | 2 [47] | Wang [84] | Akhavan [87] | Teh [10] | | | |
| | | | = 8 | = 24 | | | | | | |
| NCpB | 30.85 | | 15.24 | 16.25 | 122.4 | 105.5 | 28.45 | | | |
5. Conclusions and Future Work
In this paper, we have designed and realized the two proposed keyed
CNN hash functions, conducted analysis of the computing performance, and performed security. These two structures are based on the
Sponge construction and have two hash output lengths, i.e., 256 and 512 bits. The results of analysis in terms of cryptanalytical attacks and statistical analyses are similar to those obtained by the standard hash algorithm
SHA-3. For the computing performance term, the results of our two proposed structures are less than the standard hash algorithm
SHA-3 due to the sequential implementation. For a parallel implementation using 50 output neurons [
66], the computing performance of Structure 2 with
= 8 will be better than
SHA-3. Then, the proposed
keyed-Sponge CNN hash functions can be used in Digital Signature, Message Authentication, and Data Integrity applications.
Our future work will focus on the Extendable-Output Functions (XOFs), based on the keyed-Sponge CNN (CNN-SHAKE), where the proposed structures can produce hash outputs with variable length (as per user request). In addition, we will design and realize a new CNN structure based on the Duplex construction (CNN-DUPLEX) that will be useful for Authenticated Encryption with Associated Data (AEAD) applications.