A Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy and Its Application to Multivariate Signal of Rotating Machinery
Abstract
1. Introduction
2. Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy
2.1. Multivariate Fluctuating Dispersion Entropy (MFDE)
- (1)
- The multivariate time series is mapped to using a normal distribution functionwhere is the expected value and is the variance.
- (2)
- The linear transformation maps Y to .where c is an integer and int(·) represents the rounding function. According to the multi-variable embedding theory, the embedding vector is calculated by:where . The embedding dimension vector , The delay coefficient vector . Convert to ,
- (3)
- According to the definition of Shannon entropy, the multivariate fluctuation dispersion entropy of the original signal is:
2.2. Multivariate Multiscale Fluctuation Dispersion Entropy (MMFDE)
- (1)
- For a multivariable time series, with length L and number of signal channels N. Then, the coarse granulation time series of scale factor is:
- (2)
- MMFDE was obtained by calculating the MFDE of each coarse-grained multivariate time series under the same parameters. By extending the single-scale MFDE to the multi-scale, more information is obtained from the multi-scale coarse-grained time series of different scales to obtain the multi-scale MMFDE. However, in the coarse-grained multivariate time series whose MMFDE scale factor is , only the coarse-grained multivariate time series starting with is considered, and the remaining multivariable time series is missing. The relationship between the coarse-grained time series has not been taken into consideration, resulting in the lack of statistical information.
2.3. Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy (RCMMFDE)
- (1)
- For a multivariable time series with length L and number of signal channels N, the coarse-grained time series for the given scale factor is , where , where , .
- (2)
- The RCMMFDE of the original multivariable time series is:where m is the embedding dimension, c is the number of categories, d denotes the delay coefficient, represent the scale factor. is the average probability of the dispersion mode of coarse-grained sequence . is the frequency of scattering mode in the A multivariate coarse-grained time series .
2.4. RCMMFDE Feature Analysis
2.4.1. Mixed Analysis of White Noise and 1/f Noise
2.4.2. Analysis of Anti-Noise Performance
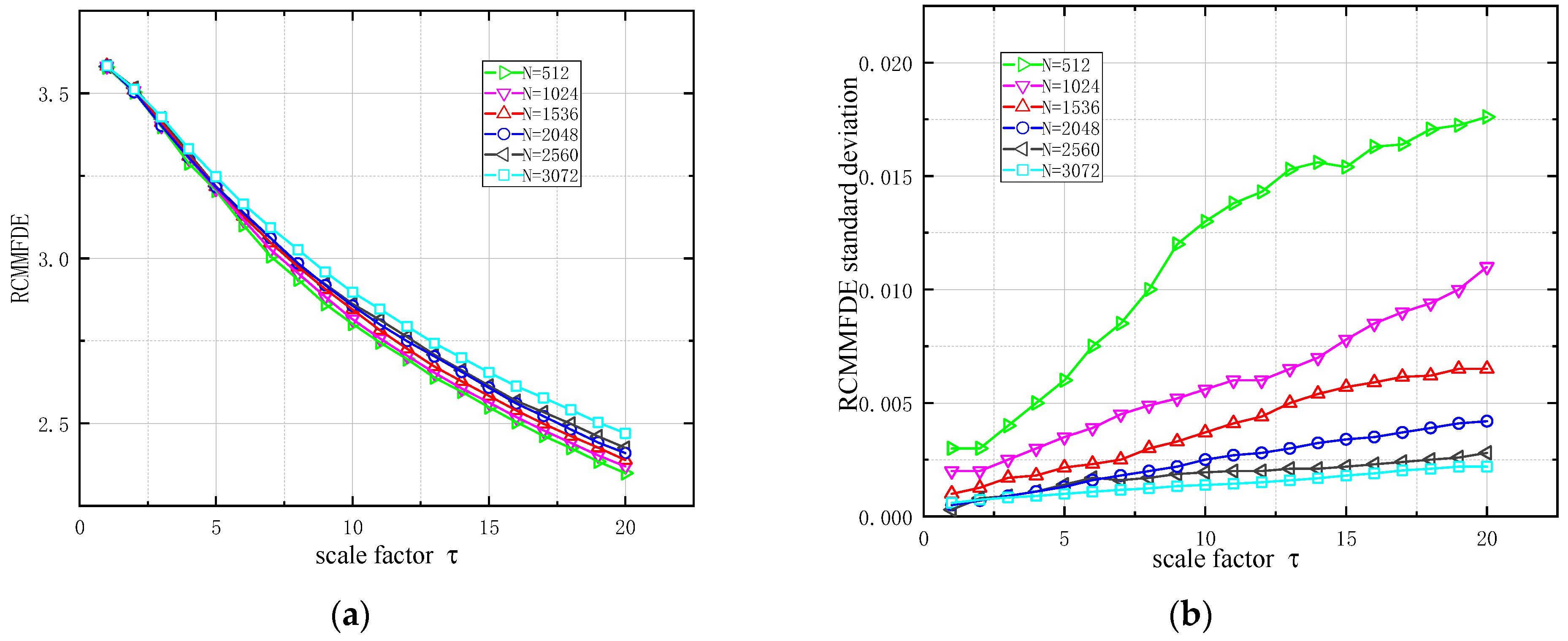
2.4.3. RCMMFDE Data Length Sensitivity Analysis
2.5. Fault Diagnosis Based on RCMMFDE
2.5.1. JMIM Feature Selection
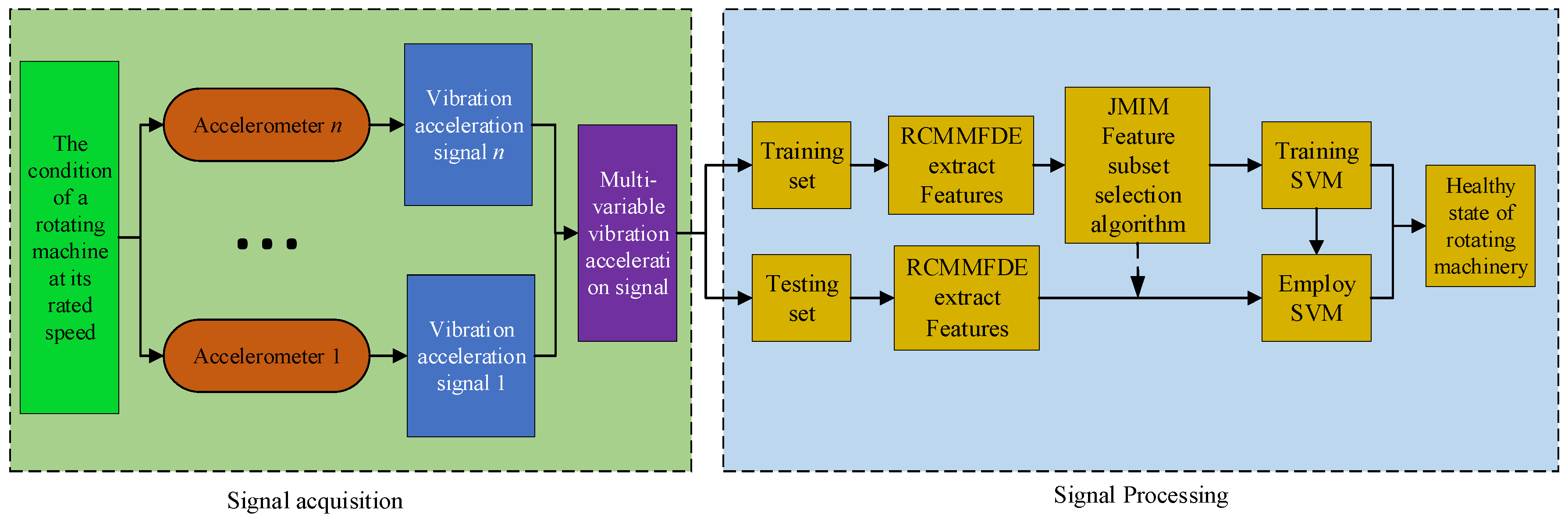
2.5.2. RCMMFDE-JMIM-SVM Fault Diagnosis Algorithm
- Step 1.
- Signal acquisition: Through acceleration sensors installed at different positions of the rotating machinery to be monitored, multi-channel vibration signals of the rotating machinery under different speeds are collected. The data samples collected under different running speeds can form a fault sample data set.
- Step 2.
- Feature extraction: RCMMFDE algorithm is used to extract features from fault sample data to form feature data sets, which are divided into training data sets and test data sets.
- Step 3.
- Feature selection: JMIM algorithm is used to select the most sensitive sub-features of the feature.
- Step 4.
- SVM model training: SVM classifier is trained using sensitive features. The SVM classifier includes M-1 dichotomous SVM, where M is the type of fault sample.
- Step 5.
- Fault diagnosis: Input the samples of the test data set into the RCMMFDE-JMIM-SVM classifier to identify the fault types of different bearing samples.
3. Experimental Verification and Analysis
3.1. Validation of Gearbox Fault Data Set
3.1.1. Data Set Description
3.1.2. RCMMFDE-JMIM-SVM Sensitive Feature Number Analysis
3.1.3. RCMMFDE-JMIM-SVM Performance Analysis at Constant Speed
3.1.4. RCMMFDE-JMIM-SVM Performance Verification
3.2. Verification of Rolling Bearing Fault Data
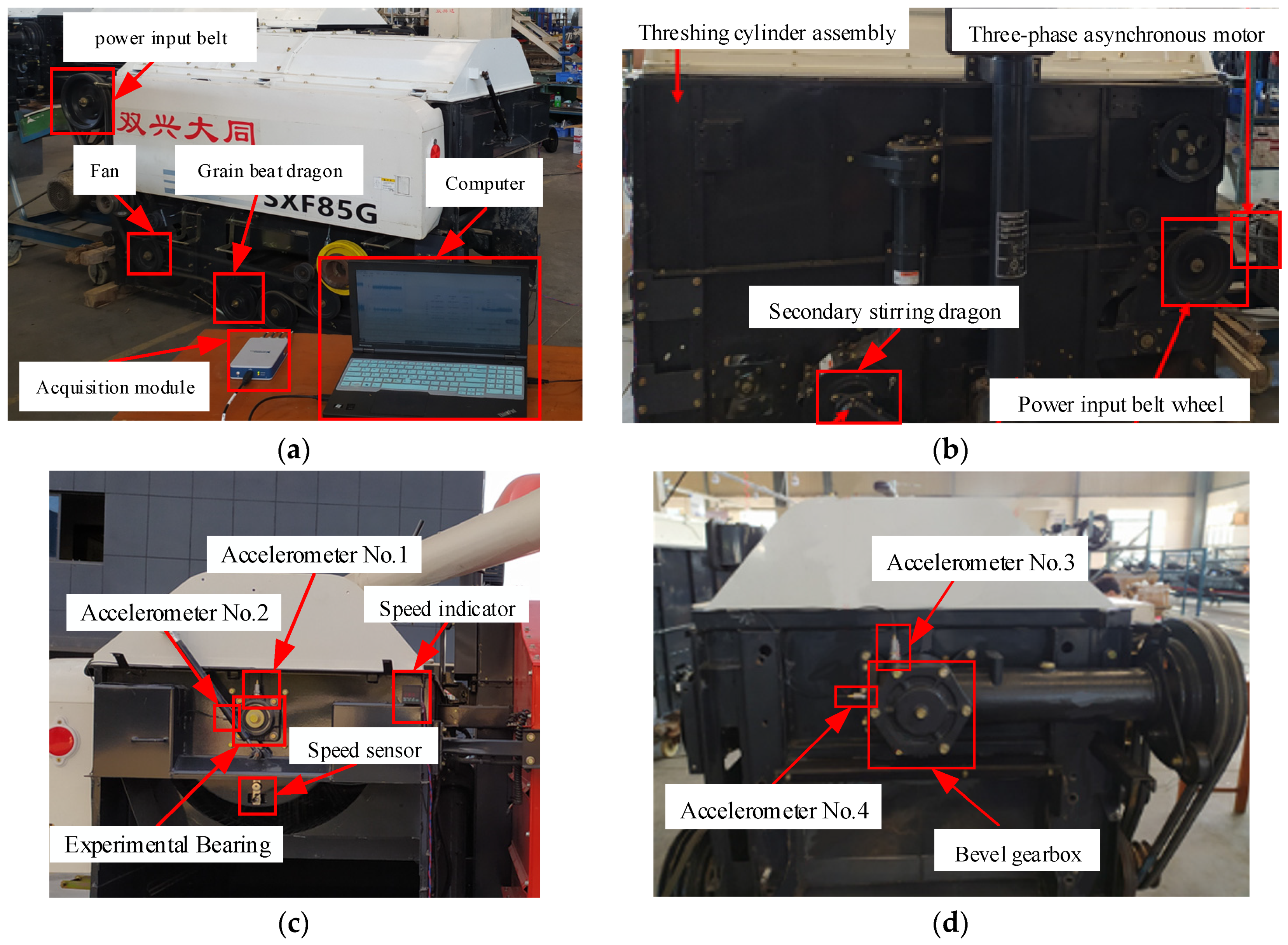
3.2.1. Description of Rolling Bearing Fault Data Set
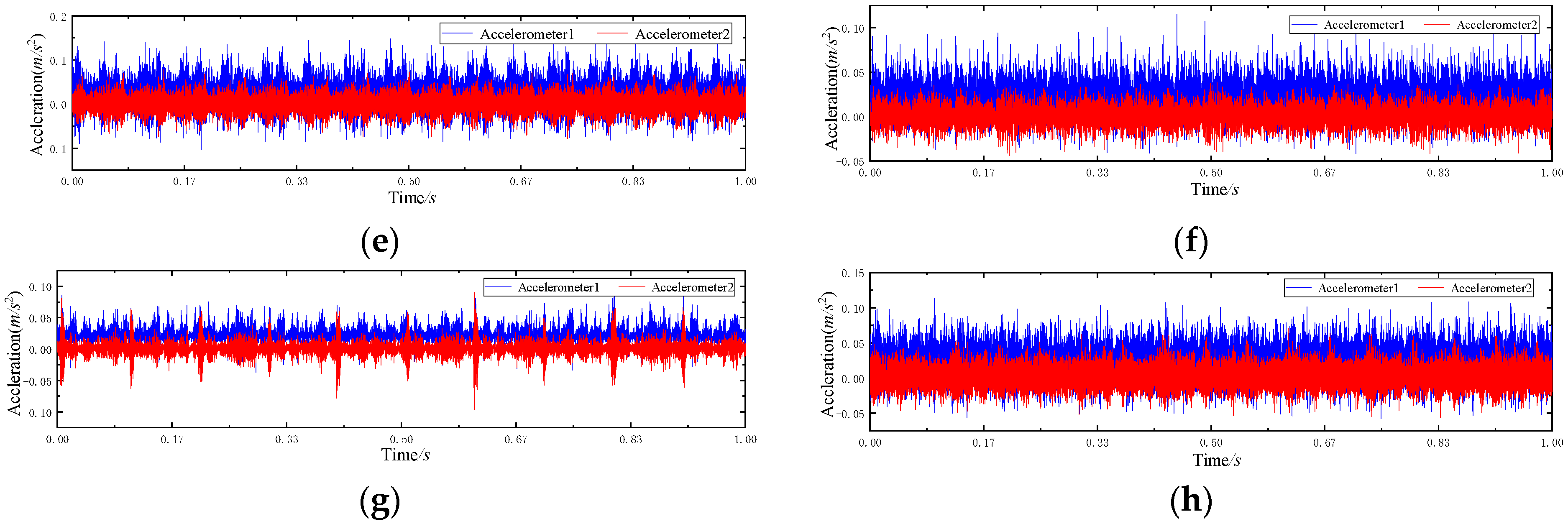
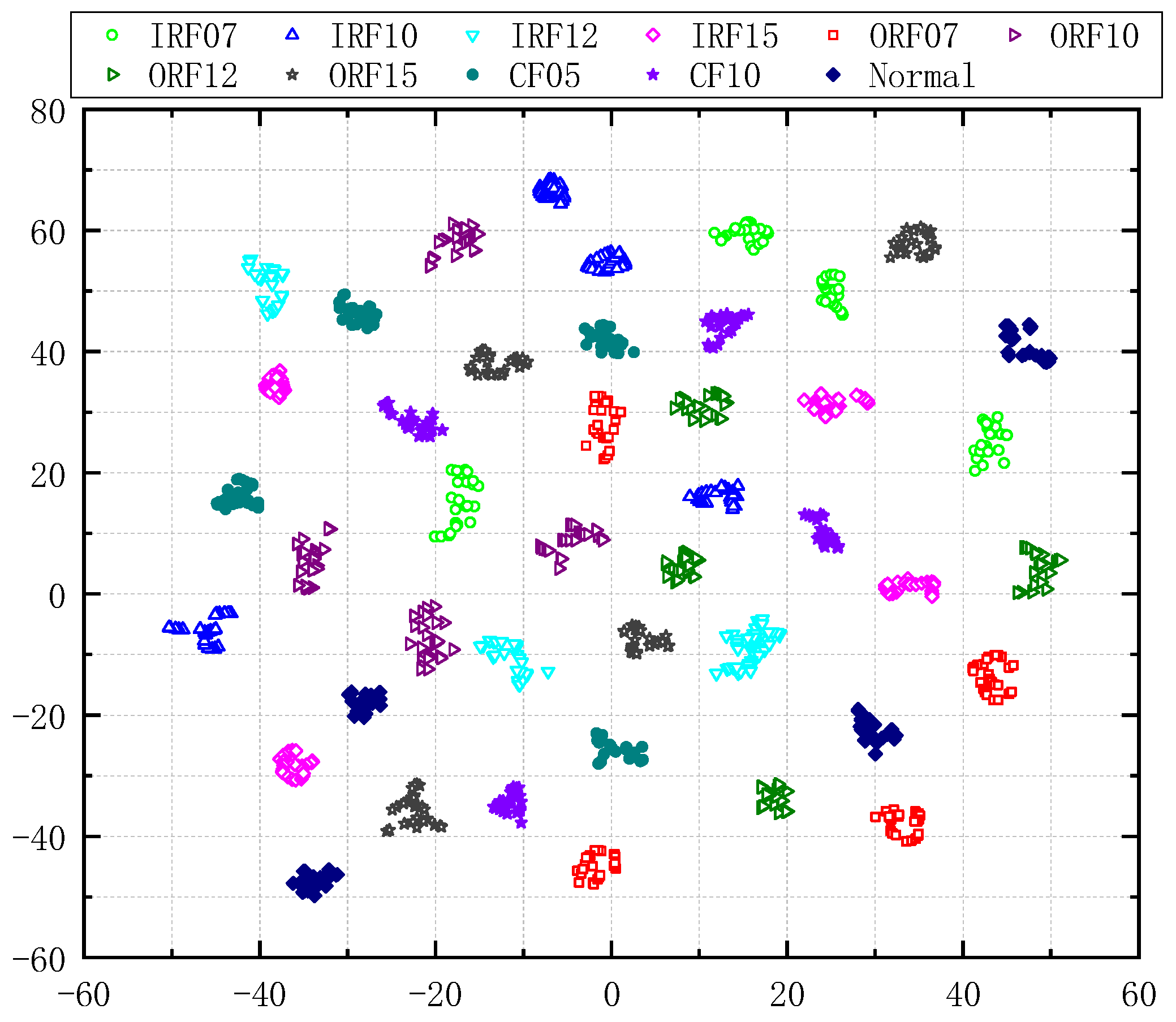
3.2.2. Rolling Bearing Fault Data Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, T. Rolling-bearings fault diagnosis based-on empirical mode decomposition and least square support vector machine. J. Mech. Eng. 2007, 43, 88–92. [Google Scholar] [CrossRef]
- Duan, Z.; Wu, T.; Guo, S.; Shao, T.; Malekian, R.; Li, Z. Development and trend of condition monitoring and fault diagnosis of multi-sensors information fusion for rolling bearings: A review. Int. J. Adv. Manuf. Technol. 2018, 96, 803–819. [Google Scholar] [CrossRef]
- De Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A review of wind turbine bearing condition monitoring: State of the art and challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, S.; Pan, H.; Jiang, K. An improved empirical wavelet transform and refined composite multiscale dispersion entropy based fault diagnosis method for rolling bearing. IEEE Access 2019, 8, 168732–168742. [Google Scholar] [CrossRef]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 2002, 38, 713–718. [Google Scholar] [CrossRef]
- Porta, A.; Bari, V.; De Maria, B.; Cairo, B.; Vaini, E.; Malacarne, M.; Pagani, M.; Lucini, D. On the Relevance of Computing a Local Version of Sample Entropy in Cardiovascular Control Analysis. IEEE Trans. Biomed. Eng. 2019, 3, 623–631. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate Entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Han, M.; Pan, J. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 76, 7–19. [Google Scholar] [CrossRef]
- Richman, J.S.; Lake, D.E.; Moorman, J.R. Sample Entropy. Method Enzym. 2004, 384, 172–184. [Google Scholar]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Rostaghi, M.; Ashory, M.R.; Azami, H. Application of dispersion entropy to status characterization of rotary machines. J. Sound Vib. 2019, 438, 291–308. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude- and Fluctuation-Based Dispersion Entropy. Entropy 2018, 20, 210. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Arnold, S.E.; Sanei, S.; Chang, Z.; Sapiro, G.; Escudero, J.; Gupta, A.S. Multiscale Fluctuation-based Dispersion Entropy and its Applications to Neurological Diseases. IEEE Access 2019, 7, 68718–68733. [Google Scholar] [CrossRef]
- Gan, X.; Lu, H.; Yang, G. Fault Diagnosis Method for Rolling Bearings Based on Composite Multiscale Fluctuation Dispersion Entropy. Entropy 2019, 21, 290. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Yang, X.; Shen, J.; Liu, W. Fault Diagnosis of Hydraulic Pumps Using PSO-VMD and Refined Composite Multiscale Fluctuation Dispersion Entropy. Shock Vib. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Azami, H.; Fernandez, A.; Escudero, J. Multivariate Multiscale Dispersion Entropy of Biomedical Times Series. Entropy 2017, 21, 913. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, H.; Yin, J.; Xu, M.; Chen, Y. Refined composite multivariate multiscale symbolic dynamic entropy and its application to fault diagnosis of rotating machine. Measurement 2020, 151, 107233. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate Multiscale Entropy Analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Zheng, J.; Tu, D.; Pan, H.; Hu, X.; Liu, T.; Liu, Q. A Refined Composite Multivariate Multiscale Fuzzy Entropy and Laplacian Score-Based Fault Diagnosis Method for Rolling Bearings. Entropy 2017, 19, 585. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J.; Fernández, A. Refined composite multivariate multiscale entropy based on variance for analysis of resting-state magnetoencephalograms in Alzheimer’s disease. In Proceedings of the 2016 International Conference for Students on Applied Engineering (ICSAE), Newcastle upon Tyne, UK, 20–21 October 2016; pp. 413–418. [Google Scholar] [CrossRef]
- Bennasar, M.; Hicks, Y.; Setchi, R. Feature selection using Joint Mutual Information Maximisation. Expert Syst. Appl. 2015, 42, 8520–8532. [Google Scholar] [CrossRef]
- Mao, Y.; Cao, H.; Ping, P.; Li, X. Feature selection based on maximum conditional and joint mutual information. J. Comput. Appl. 2019, 39, 734–741. [Google Scholar]
- Rajlakshmi, S.; Sane, S. JMIM: A Feature Selection Technique using Joint Mutual Information Maximization Approach. Int. J. Comput. Appl. 2017, 975, 8887. [Google Scholar]
- Dao, T.K.; Nguyen, T.T.; Pan, J.S.; Qiao, Y.; Lai, Q.A. Identification Failure Data for Cluster Heads Aggregation in WSN based on Improving Classification of SVM. IEEE Access 2020, 8, 61070–61084. [Google Scholar] [CrossRef]
- Venkatesan, C.; Karthigaikumar, P.; Paul, A.; Satheeskumaran, S.; Kumar, R.J. ECG Signal Preprocessing and SVM Classifier-Based Abnormality Detection in Remote Healthcare Applications. IEEE Access 2018, 6, 9767–9773. [Google Scholar] [CrossRef]
- Mao, X.; Wang, L.; Li, C. SVM Classifier for Analog Fault Diagnosis Using Fractal Features. In Proceedings of the Second International Symposium on Intelligent Information Technology Application (IITA’08), Shanghai, China, 20–22 December 2008. [Google Scholar]
- Azami, H.; Rostaghi, M.; Escudero, J. Refined Composite Multiscale Dispersion Entropy: A Fast Measure of Complexity. arXiv 2016, arXiv:1606.01379. [Google Scholar]
- Laurens, V.D.M.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]











| Abbreviation | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | |
|---|---|---|---|---|---|---|---|---|---|
| Shaft | Input | Normal | Normal | Normal | Normal | Normal | ISI | Normal | ISI |
| Output | Normal | Normal | Normal | Normal | Normal | Normal | Keyway wear | Normal | |
| Bearing | Input shaft—Input end | Normal | Normal | Normal | BBF | BIF | BIF | BIF | Normal |
| Intermediate shaft— Input shaft | Normal | Normal | Normal | Normal | BBF | BBF | Normal | BBF | |
| Output shaft—Input end | Normal | Normal | Normal | Normal | BOF | BOF | Normal | BOF | |
| Input shaft—Output end | Normal | Normal | Normal | Normal | Normal | Normal | Normal | Normal | |
| Intermediate shaft— Output end | Normal | Normal | Normal | Normal | Normal | Normal | Normal | Normal | |
| Output shaft—Output end | Normal | Normal | Normal | Normal | Normal | Normal | Normal | Normal | |
| Gear | 32T | Normal | TSC | Normal | Normal | TSC | Normal | Normal | Normal |
| 96T | Normal | Normal | Normal | Normal | Normal | Normal | Normal | Normal | |
| 48T | Normal | GI | GI | GI | GI | Normal | Normal | Normal | |
| 80T | Normal | Normal | Normal | TRF | TRF | TRF | Normal | Normal | |
| No | State | Training Samples | Testing Samples | Class Label |
|---|---|---|---|---|
| 1 | G1 | 200 | 100 | 1,0,0,0,0,0,0,0 |
| 2 | G2 | 200 | 100 | 0,1,0,0,0,0,0,0 |
| 3 | G3 | 200 | 100 | 0,0,1,0,0,0,0,0 |
| 4 | G4 | 200 | 100 | 0,0,0,1,0,0,0,0 |
| 5 | G5 | 200 | 100 | 0,0,0,0,1,0,0,0 |
| 6 | G6 | 200 | 100 | 0,0,0,0,0,1,0,0 |
| 7 | G7 | 200 | 100 | 0,0,0,0,0,0,1,0 |
| 8 | G8 | 200 | 100 | 0,0,0,0,0,0,0,1 |
| Method | Parameter | |||||
|---|---|---|---|---|---|---|
| RCMMFE-JMIM-SVM | = 17 | m = 2 | r = 0.15 | d = 1 | = 25 | f = 2 |
| RCMMSE-JMIM-SVM | = 12 | m = 2 | r = 0.15 | d = 1 | = 25 | |
| RCMMPE-JMIM-SVM | = 17 | m = 2 | = 17 | |||
| RCMMFDE-JMIM-SVM | = 20 | m = 2 | c = 6 | d = 1 | = 25 | |
| Method | Max Accuracy | Min Accuracy | Average Accuracy | Run Time |
|---|---|---|---|---|
| RCMMFDE-JMIM-SVM | 99.252 | 98.518 | 98.757 | 1.67 |
| RCMMSE-JMIM-SVM | 96.882 | 96.215 | 96.648 | 1.14 |
| RCMMPE-JMIM-SVM | 94.045 | 93.217 | 93.554 | 148.79 |
| RCMMFE-JMIM-SVM | 97.867 | 97.305 | 97.694 | 8.28 |
| State | Testing Samples | Accuracy/% | ||||
|---|---|---|---|---|---|---|
| RCMMFDE-JMIM-SVM | RCMMFE-JMIM-SVM | RCMMSE-JMIM-SVM | RCMMPE-JMIM-SVM | CFVS-SVM | ||
| G1 | 180 | 99.425 | 98.627 | 98.129 | 96.951 | 97.273 |
| G2 | 180 | 99.354 | 97.056 | 97.281 | 91.488 | 94.445 |
| G3 | 180 | 97.812 | 95.627 | 98.835 | 97.538 | 97.758 |
| G4 | 180 | 99.489 | 97.566 | 95.756 | 92.157 | 95.561 |
| G5 | 180 | 99.105 | 97.634 | 96.018 | 92.266 | 93.891 |
| G6 | 180 | 99.281 | 98.461 | 96.485 | 94.137 | 96.659 |
| G7 | 180 | 99.577 | 97.343 | 97.528 | 94.513 | 96.562 |
| G8 | 180 | 98.907 | 96.932 | 94.414 | 93.064 | 94.827 |
| Total | 900 | 99.173 | 97.782 | 96.619 | 93.751 | 94.658 |
| Bearing State | Abbreviation | Fault Width (mm) | Fault Depth (mm) | Threshing Cylinder Speed (r/min) |
|---|---|---|---|---|
| Normal | Normal | 0 | 0 | 80/160/240/320 |
| Outer Ring Fault 1 | IRF07 | 0.7 | 3.7 | 80/160/240/320 |
| Outer Ring Fault 2 | IRF10 | 1.0 | 3.7 | 80/160/240/320 |
| Outer Ring Fault 3 | IRF12 | 1.2 | 3.7 | 80/160/240/320 |
| Outer Ring Fault 4 | IRF15 | 1.5 | 3.7 | 80/160/240/320 |
| Outer Ring Fault 1 | ORF07 | 0.7 | 3.2 | 80/160/240/320 |
| Outer Ring Fault 2 | ORF10 | 1.0 | 3.2 | 80/160/240/320 |
| Outer Ring Fault 3 | ORF12 | 1.2 | 3.2 | 80/160/240/320 |
| Outer Ring Fault4 | ORF15 | 1.5 | 3.2 | 80/160/240/320 |
| Composite Fault 1 | CF05 | 0.5/0.5 | 3.2/3.7 | 80/160/240/320 |
| Composite Fault 2 | CF10 | 1.0/1.0 | 3.2/3.7 | 80/160/240/320 |
| Bearing State | Testing Samples | RCMMFDE-JMIM-SVM | RCMMFE-JMIM-SVM | RCMMSE-JMIM-SVM | RCMMPE-JMIM-SVM | CFVS-SVM | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MCR | Acc/% | MCR | Acc/% | MCR | Acc/% | MCR | Acc/% | MCR | Acc/% | ||
| Normal | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | CF05 | 96.00 |
| IRF07 | 25 | 0 | 100.00 | 0 | 100.00 | IRF10 | 96.00 | IRF12 | 88.00 | IRF10 | 92.00 |
| IRF10 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | IRF07 | 96.00 | 0 | 100.00 |
| IRF12 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | IRF10 | 96.00 |
| IRF15 | 25 | 0 | 100.00 | 0 | 100.00 | IRF12 | 96.00 | 0 | 100.00 | 0 | 100.00 |
| ORF07 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | ORF10 | 88.00 |
| ORF10 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | ORF15 | 96.00 | 0 | 100.00 |
| ORF12 | 25 | 0 | 100.00 | 0 | 100.00 | ORF12 | 92.00 | ORF10 | 96.00 | 0 | 100.00 |
| ORF15 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | ORF12 | 96.00 |
| CF05 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | CF10 | 96.00 | 0 | 100.00 |
| CF10 | 25 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | 0 | 100.00 | CF05 | 96.00 |
| Total | 275 | 0 | 100.00 | 0 | 100.00 | 4 | 99.27 | 7 | 97.46 | 9 | 96.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, C.; Yang, G.; Liu, L.; Jiang, H.; Chen, X. A Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy and Its Application to Multivariate Signal of Rotating Machinery. Entropy 2021, 23, 128. https://doi.org/10.3390/e23010128
Xi C, Yang G, Liu L, Jiang H, Chen X. A Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy and Its Application to Multivariate Signal of Rotating Machinery. Entropy. 2021; 23(1):128. https://doi.org/10.3390/e23010128
Chicago/Turabian StyleXi, Chenbo, Guangyou Yang, Lang Liu, Hongyuan Jiang, and Xuehai Chen. 2021. "A Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy and Its Application to Multivariate Signal of Rotating Machinery" Entropy 23, no. 1: 128. https://doi.org/10.3390/e23010128
APA StyleXi, C., Yang, G., Liu, L., Jiang, H., & Chen, X. (2021). A Refined Composite Multivariate Multiscale Fluctuation Dispersion Entropy and Its Application to Multivariate Signal of Rotating Machinery. Entropy, 23(1), 128. https://doi.org/10.3390/e23010128





