Figure 1.
Underlying Fréchet (), . (a) The means of ln-quantile estimators with the true (). (b) The RMSE of Ln-quantile estimation, ,
Figure 1.
Underlying Fréchet (), . (a) The means of ln-quantile estimators with the true (). (b) The RMSE of Ln-quantile estimation, ,
Figure 2.
Underlying (), , (a) The means of ln-quantile estimators with the true (b) The RMSE of Ln-quantile estimation, , .
Figure 2.
Underlying (), , (a) The means of ln-quantile estimators with the true (b) The RMSE of Ln-quantile estimation, , .
Figure 3.
Underlying (2), , (a) The means of ln-quantile estimators with the true (). (b) The RMSE of ln-quantile estimators, ,
Figure 3.
Underlying (2), , (a) The means of ln-quantile estimators with the true (). (b) The RMSE of ln-quantile estimators, ,
Figure 4.
(0.25) model, 95% confidence interval of quantile estimators, , Note that (purple) has shortest CI with length 0.2668. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 4.
(0.25) model, 95% confidence interval of quantile estimators, , Note that (purple) has shortest CI with length 0.2668. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 5.
The (0.5) model, 95% confidence interval of quantile estimators, Note that (purple) has shortest CI with length 0.7094. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 5.
The (0.5) model, 95% confidence interval of quantile estimators, Note that (purple) has shortest CI with length 0.7094. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 6.
The (2) model, 95% confidence interval of quantile estimators Note that (purple) has shortest CI with length 2.2511. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 6.
The (2) model, 95% confidence interval of quantile estimators Note that (purple) has shortest CI with length 2.2511. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 7.
Flu original data from 1 January 1997 to December 31 2019, 994 weeks, (a) Flu chart of type A flu viruses detected in Canada, and 111 weeks remaining after the threshold, of average 953 flu viruses. (b) Histogram of the number of type A flu viruses detected in Canada.
Figure 7.
Flu original data from 1 January 1997 to December 31 2019, 994 weeks, (a) Flu chart of type A flu viruses detected in Canada, and 111 weeks remaining after the threshold, of average 953 flu viruses. (b) Histogram of the number of type A flu viruses detected in Canada.
Figure 8.
After threshold 953 flu viruses, Flu transformation data, (a) Log-log plot of flu in Canada example. (b) Estimate GPD curve and the 99% high quantile and histogram of the distribution of type A flu viruses detested weekly.
Figure 8.
After threshold 953 flu viruses, Flu transformation data, (a) Log-log plot of flu in Canada example. (b) Estimate GPD curve and the 99% high quantile and histogram of the distribution of type A flu viruses detested weekly.
Figure 9.
For flu in the Canadian data, (a) Estimates of the second-order parameter and , (b) Estimates and (c) Tail index estimators, H, (d) ln-quantile estimators, The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level.
Figure 9.
For flu in the Canadian data, (a) Estimates of the second-order parameter and , (b) Estimates and (c) Tail index estimators, H, (d) ln-quantile estimators, The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level.
Figure 10.
95% confidence interval of three ln-quantile estimators after the threshold 953 for the flu in Canada example. , Note that (purple) has shortest CI with length 0.7966. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 10.
95% confidence interval of three ln-quantile estimators after the threshold 953 for the flu in Canada example. , Note that (purple) has shortest CI with length 0.7966. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 11.
Two weeks plot of gamma ray & X ray from July 2 to 16, 2012.
Figure 11.
Two weeks plot of gamma ray & X ray from July 2 to 16, 2012.
Figure 12.
Gamma ray original data from November 2008 to April 2017, (a) Gamma ray released V.S solar flare occurred. After the threshold of 86 million counts, flares remaining. (b) Histogram of gamma ray released from solar flares.
Figure 12.
Gamma ray original data from November 2008 to April 2017, (a) Gamma ray released V.S solar flare occurred. After the threshold of 86 million counts, flares remaining. (b) Histogram of gamma ray released from solar flares.
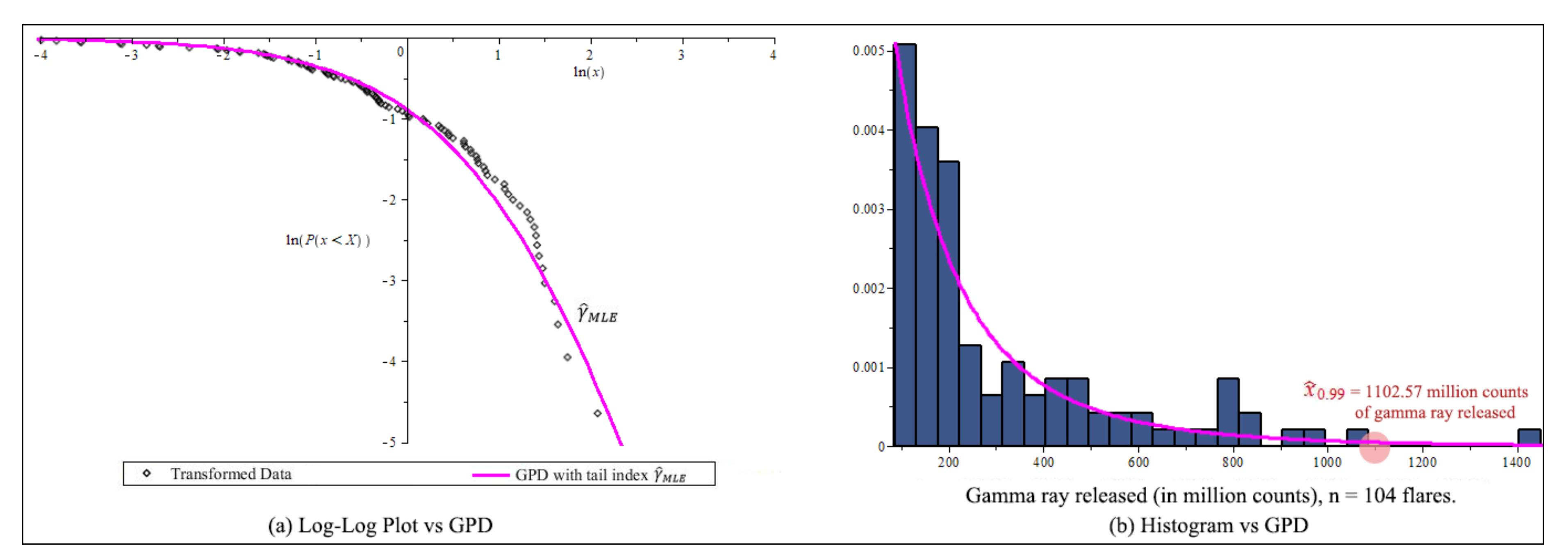
Figure 13.
After threshold 86 millions count, transformation data, (a) Log-log plot of gamma ray from solar flare example. (b) The Estimate GPD and the 99% high quantile of the distribution of gamma ray released by solar flare.
Figure 13.
After threshold 86 millions count, transformation data, (a) Log-log plot of gamma ray from solar flare example. (b) The Estimate GPD and the 99% high quantile of the distribution of gamma ray released by solar flare.
Figure 14.
For gamma ray of solar flare example, (a) Estimates of the second-order parameters and , , (b) Estimates and (c) Tail index estimators, H, . (d) ln-quantile estimators, The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level.
Figure 14.
For gamma ray of solar flare example, (a) Estimates of the second-order parameters and , , (b) Estimates and (c) Tail index estimators, H, . (d) ln-quantile estimators, The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level.
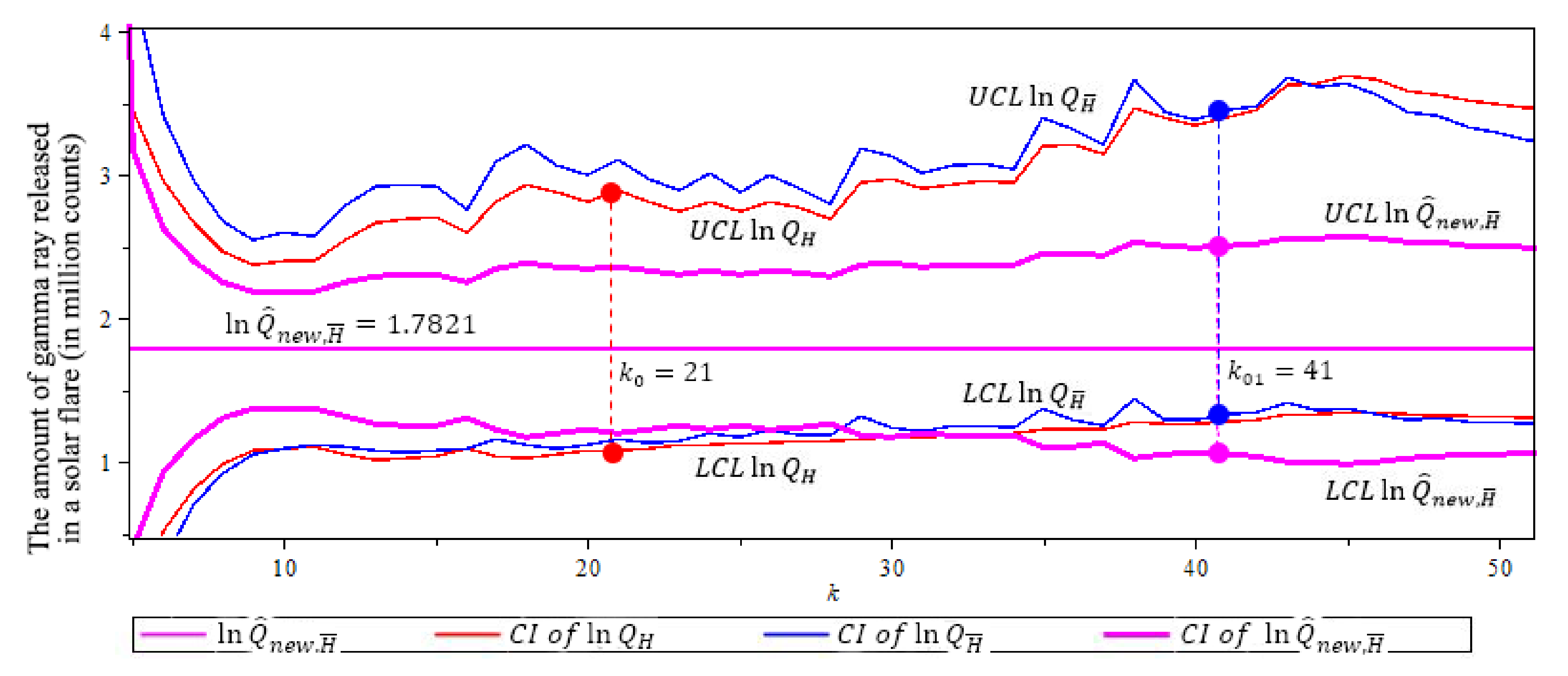
Figure 15.
95% confidence interval of three ln-quantile estimators after threshold of 86 million counts for the gamma ray example. , Note that (purple) has shortest CI with length 1.4451. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Figure 15.
95% confidence interval of three ln-quantile estimators after threshold of 86 million counts for the gamma ray example. , Note that (purple) has shortest CI with length 1.4451. (The solid circles “•” in the plot are the values of the quantile estimators at their optimal k level).
Table 1.
The four ln-quantile estimators we use in simulations.
Table 1.
The four ln-quantile estimators we use in simulations.
| Quantile Estimators | Defined in | Tail Index Estimator |
|---|
| (6) | H in (5) |
| (7) | H in (5) |
| | in (9) |
| (19) | in (9) |
Table 2.
Fréchet (, . Mean, MSE, REFF of the Estimators. The highest REFF values are in bold.
Table 2.
Fréchet (, . Mean, MSE, REFF of the Estimators. The highest REFF values are in bold.
| n | 500 | 1000 | 2000 | 5000 |
| 1.7268 | 1.9002 | 2.0735 | 2.3026 |
| 126 | 200 | 318 | 585 |
| 1.1218 | 1.1400 | 0.4991 | −0.0357 |
| Mean (MSE) | 1.8526 (0.0429) | 2.0038 (0.0300) | 2.1657 (0.0228) | 2.3755 (0.0147) |
| | REFF | 1 | 1 | 1 | 1 |
| Mean (MSE) | 1.7906 (0.0219) | 1.9540 (0.0154) | 2.1239 (0.0115) | 2.3431 (0.0074) |
| | REFF | 1.4004 | 1.3933 | 1.4104 | 1.4125 |
| Mean (MSE) | 1.7092 (0.0206) | 1.8849 (0.0141) | 2.0764 (0.0111) | 2.3073 (0.0072) |
| | REFF | 1.4419 | 1.4576 | 1.4347 | 1.4257 |
| Mean (MSE) | 1.7185 (0.0095) | 1.8791 (0.0065) | 2.0716 (0.0051) | 2.2798 (0.0044) |
| | REFF | 2.1252 | 2.1399 | 2.1139 | 1.8231 |
Table 3.
GPD ( . Mean, MSE, REFF of the estimators. The highest REFF values are in bold.
Table 3.
GPD ( . Mean, MSE, REFF of the estimators. The highest REFF values are in bold.
| n | 500 | 1000 | 2000 | 5000 |
| 4.1149 | 4.4710 | 4.8242 | 5.2883 |
| 34 | 48 | 68 | 107 |
| −0.7512 | −0.7482 | −0.7427 | −0.7244 |
| Mean (MSE) | 4.7019 (0.6349) | 4.9773 (0.4863) | 5.3065 (0.4554) | 5.7209 (0.3427) |
| | REFF | 1 | 1 | 1 | 1 |
| Mean (MSE) | 4.2913 (0.2172) | 4.6258 (0.1628) | 4.9904 (0.1491) | 5.4485 (0.1074) |
| | REFF | 1.7159 | 1.7282 | 1.7478 | 1.7865 |
| Mean (MSE) | 4.1140 (0.1654) | 4.4801 (0.1267) | 4.8656 (0.1166) | 5.3434 (0.0825) |
| | REFF | 1.9663 | 1.9591 | 1.9763 | 2.0379 |
| Mean (MSE) | 3.9076 (0.0779) | 4.4239 (0.0233) | 4.8674 (0.0241) | 5.4359 (0.0382) |
| | REFF | 2.8657 | 4.5666 | 4.3428 | 2.9954 |
Table 4.
GPD( Mean, MSE, REFF of the estimators. The highest REFF values are in bold.
Table 4.
GPD( Mean, MSE, REFF of the estimators. The highest REFF values are in bold.
| n | 500 | 1000 | 2000 | 5000 |
| 13.1224 | 14.5087 | 15.8949 | 17.7275 |
| 170 | 269 | 515 | 1071 |
| −2.7893 | −2.8417 | −2.8687 | −3.1684 |
| Mean (MSE) | 13.6276 (1.3232) | 14.9415 (0.9745) | 16.2733 (0.6548) | 18.0099 (0.3833) |
| | REFF | 1 | 1 | 1 | 1 |
| Mean (MSE) | 13.4502 (0.9965) | 14.8004 (0.7283) | 16.1618 (0.4779) | 17.9283 (0.2804) |
| | REFF | 1.1523 | 1.1567 | 1.2412 | 1.1693 |
| Mean (MSE) | 13.1933 (0.8926) | 14.5960 (0.6477) | 15.9719 (0.4491) | 17.7717 (0.2751) |
| | REFF | 1.2175 | 1.2267 | 1.2075 | 1.1804 |
| Mean (MSE) | 13.0009 (0.6007) | 14.4907 (0.3680) | 15.8926 (0.3070) | 17.6429 (0.2127) |
| | REFF | 1.4841 | 1.6274 | 1.4606 | 1.3426 |
Table 5.
efficiencies of 95% CI for .
Table 5.
efficiencies of 95% CI for .
| | of | at Optimal k | Length | | | |
|---|
| | | 165 | 0.5142 | 1 | 94.2% | 1 |
| Fréchet (0.25) | | 395 | 0.3564 | 1.4517 | 96.7% | 0.4706 |
| | | 395 | 0.2668 | 1.9275 | 99.6% | 0.1739 |
| | | 28 | 2.4922 | 1 | 47.4% | 1 |
| GPD(0.5) | | 93 | 1.5204 | 1.6392 | 79.0% | 2.9750 |
| | | 93 | 0.7094 | 3.5130 | 99.6% | 10.3478 |
| | | 270 | 3.4410 | 1 | 79.7% | 1 |
| GPD(2) | | 511 | 2.7291 | 1.2609 | 83.2% | 1.2966 |
| | | 511 | 2.2511 | 1.5286 | 99.6% | 3.3261 |
Table 6.
The goodness-of-fit tests under the model for the flu in Canada data.
Table 6.
The goodness-of-fit tests under the model for the flu in Canada data.
| | Goodness-of-Fit Tests |
|---|
| | K-S Test | A-D Test | C-v-M Test |
|---|
| | | p-Value | | -Value | | -Value |
|---|
| 0.0628 | 0.6406 | 0.4475 | 0.8007 | 0.0621 | 0.8006 |
Table 7.
and under the model for the flu in Canada data by using .
Table 7.
and under the model for the flu in Canada data by using .
| | Absolute Errors () | Integrated Errors () |
|---|
| | | |
| | | | | | | |
| 0.0450 | 0.0450 | 0.0628 | 0.0085 | 0.0071 | 0.0074 |
Table 8.
Estimated and for the flu in Canada data. (Unit: Type A flu viruses).
Table 8.
Estimated and for the flu in Canada data. (Unit: Type A flu viruses).
| Estimation | | | Mean | Median | | |
|---|
| | 0.4370 | 3219.29 | 2257.03 | 4519.70 | 8159.10 |
| | 0.3736 | 2989.93 | 2130.78 | 3736.80 | 6031.79 |
| | 0.3736 | 2989.93 | 1690.07 | 2924.80 | 5499.85 |
Table 9.
The 95% confidence interval for and .
Table 9.
The 95% confidence interval for and .
| k | |
( | | Length | |
|---|
| | 0.6920 | 1.7312 | 2.1452 | 1.4531 | 1 |
| ( | | (3502.14) | (8159.10) | (11854.31) | (8352.17) | (1) |
| | 0.7929 | 1.3814 | 1.9698 | 1.1770 | 1.2346 |
| ( | | (3772.58) | (6031.78) | (10101.19) | (6328.21) | (1.3197) |
| | 0.8724 | 1.2707 | 1.6690 | 0.7966 | 1.8242 |
| ( | | (4006.07) | (5499.85) | (7724.49) | (3718.42) | (2.2462) |
Table 10.
Compare the goodness-of-fit tests under the model for the gamma ray data.
Table 10.
Compare the goodness-of-fit tests under the model for the gamma ray data.
| | Goodness-of-Fit Tests |
|---|
| | Test | Test | Test |
|---|
| | | p-Value | | -Value | | -Value |
|---|
| 0.0697 | 0.5750 | 0.7276 | 0.5362 | 0.0991 | 0.5893 |
Table 11.
and under the model for the gamma ray data using .
Table 11.
and under the model for the gamma ray data using .
| | Absolute Errors () | Integrated Errors () |
|---|
| | rth Highest Gamma Ray Released | rth Highest Gamma Ray Released |
|---|
| | | | | | | |
| 0.0359 | 0.0697 | 0.0697 | 0.0062 | 0.0092 | 0.0089 |
Table 12.
Estimated and in the gamma ray example. (Unit: million counts).
Table 12.
Estimated and in the gamma ray example. (Unit: million counts).
| | | Mean | Median | | |
|---|
| N/A | 0.5324 | 451.82 | 315.27 | 867.12 | 1926.04 |
| N/A | 0.6517 | 577.22 | 232.28 | 742.01 | 1958.67 |
| 0.7269 | 0.6517 | 577.22 | 189.35 | 441.60 | 1102.57 |
Table 13.
The 95% confidence interval of and
Table 13.
The 95% confidence interval of and
| k | |
( | | Length | |
|---|
| | 1.0807 | 2.3755 | 2.8864 | 1.8057 | 1 |
| ( | | (590.12) | (1926.04) | (3153.18) | (2563.06) | (1) |
| | 1.3367 | 2.3930 | 3.4494 | 2.1128 | 0.8547 |
| ( | | (737.14) | (1958.67) | (5471.71) | (4734.56) | (0.5414) |
| | 1.0595 | 1.7821 | 2.5047 | 1.4451 | 1.2495 |
| ( | | (579.55) | (1102.57) | (2179.85) | (1600.30) | (1.6016) |