Nonlinear Topological Effects in Optical Coupled Hexagonal Lattice
Abstract
:1. Introduction
2. Nonlinear Dirac Cones and Dynamical Stability
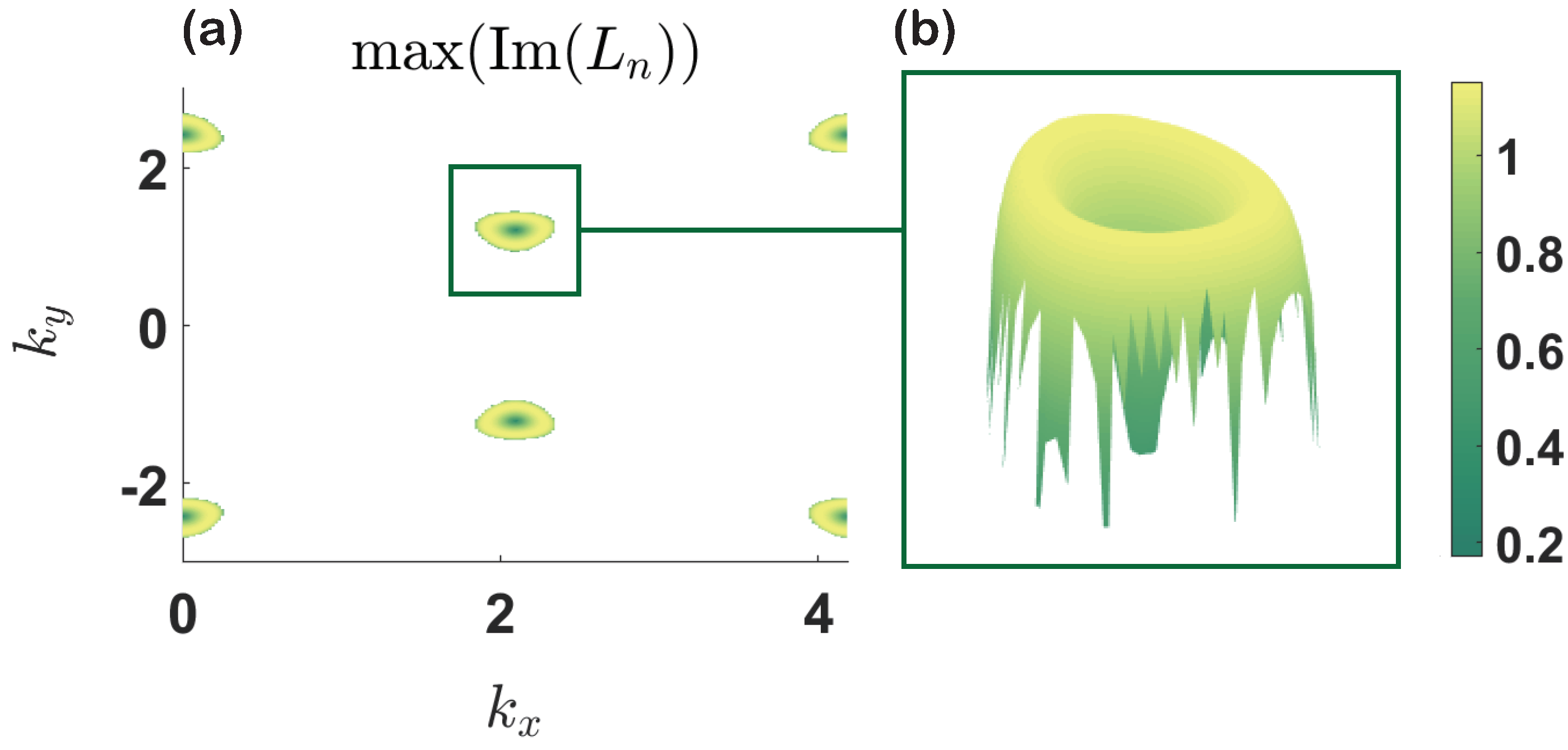
3. Nonlinear Berry Phase
4. Aharonov-Bohm (AB) Phase Accumulated in Adiabatic Transport
5. Site-Site Nonlinear Coupling, Perturbation and Noise
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AB | Aharonov-Bohm |
| NSE | Nonlinear Schrödinger equation |
| NDC | Nonlinear Dirac cone |
References
- Karplus, R.; Luttinger, J.M. Hall effect in ferromagnetics. Phys. Rev. 1954, 95, 1154. [Google Scholar] [CrossRef]
- Wen, X.G. Vacuum degeneracy of chiral spin states in compactified space. Phys. Rev. B 1989, 40, 7387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; Nijs, M. den. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef] [Green Version]
- Kohmoto, M.; Halperin, B.I.; Wu, Y.S. Diophantine equation for the three-dimensional quantum Hall effect. Phys. Rev. B 1992, 45, 13488. [Google Scholar] [CrossRef] [PubMed]
- Thouless, D.J. Quantization of particle transport. Phys. Rev. B 1983, 27, 6083. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766. [Google Scholar] [CrossRef] [Green Version]
- Xue, H.R.; Yang, Y.H.; Gao, F.; Chong, Y.D.; Zhang, B. Acoustic higher-order topological insulator on a kagome lattice. Nat. Mater. 2019, 18, 108. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.L.; Analytis, J.G.; Chu, J.H.; Liu, Z.K.; Mo, S.K.; Qi, X.L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z.; et al. Experimental Realization of a Three-Dimensional Topological Insulator Bi2Te3. Science 2009, 325, 178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H. Anomalous hall effect. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef] [Green Version]
- Yu, R.; Zhang, W.; Zhang, H.J.; Zhang, S.C.; Dai, X.; Fang, Z. Quantized Anomalous Hall Effect in Magnetic Topological Insulators. Science 2010, 329, 61. [Google Scholar] [CrossRef] [Green Version]
- Fidkowski, L.; Kitaev, A. Effects of interactions on the topological classification of free fermion systems. Phys. Rev. B 2010, 81, 134509. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Potter, A.C.; Senthil, T. Classification of Interacting Electronic Topological Insulators in Three Dimensions. Science 2014, 343, 629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, X.Y.; Schnyder, A.P. Interaction effects on the classification of crystalline topological insulators and superconductors. Phys. Rev. B 2017, 95, 195108. [Google Scholar] [CrossRef] [Green Version]
- Schnyder, A.P.; Ryu, S.; Furusaki, A.; Ludwig, A.W.W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 2008, 78, 195125. [Google Scholar] [CrossRef] [Green Version]
- Ryu, S.; Schnyder, A.P.; Furusaki, A.; Ludwig, A.W.W. Topological insulators and superconductors: Tenfold way and dimensional hierarchy. New J. Phys. 2010, 12, 065010. [Google Scholar] [CrossRef]
- Pook, W.; Hajdu, J. On the Topological Explanation of the Integer Quantum Hall Effect. Z. Phys. B-Condensed Matter 1987, 66, 427. [Google Scholar] [CrossRef]
- Simon, B.H. The Quantum Adiabatic Theorem, and Berry’s Phase. Phys. Rev. Lett. 1983, 51, 2167. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef] [Green Version]
- Chang, M.C.; Niu, Q. Berry Phase, Hyperorbits, and the Hofstadter Spectrum. Phys. Rev. Lett. 1995, 75, 1348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sundaram, G.; Niu, Q. Wave-packet dynamics in slowly perturbed crystals: Gradient corrections and Berry-phase effects. Phys. Rev. B 1999, 59, 14915. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.C.; Hu, J. A four-dimensional generalization of the quantum hall effect. Science 2001, 294, 823. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, X.W.; Zhou, X.X.; Li, C.F.; Xu, J.S.; Guo, G.C.; Zhou, Z.W. Quantum simulation of 2D topological physics in a 1D array of optical cavities. Nat. Commun. 2015, 6, 7704. [Google Scholar] [CrossRef]
- Ma, R.C.; Saxberg, B.; Owens, C.; Leung, N.; Lu, Y.; Simon, J.; Schuster, D.I. A dissipatively stabilized Mott insulator of photons. Nature 2019, 566, 51. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef] [Green Version]
- Smirnova, D.; Leykam, D.; Chong, Y.; Kivshar, Y. Nonlinear topological photonics. Appl. Phys. Rev. 2020, 7, 021306. [Google Scholar] [CrossRef]
- Galilo, B.; Lee, D.K.K.; Barnett, R. Topological Edge-State Manifestation of Interacting 2D Condensed Boson-Lattice Systems in a Harmonic Trap. Phys. Rev. Lett. 2017, 119, 203204. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.F.; Chen, X.F.; Kartashov, Y.V.; Konotop, V.V.; Ye, F.W. Coupling of Edge States and Topological Bragg Solitons. Phys. Rev. Lett. 2019, 123, 254103. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Ye, F.; Chen, X.; Kartashov, Y.V.; Torner, L.; Konotop, V.V. Topological edge states in Rashba-Dresselhaus spin-orbit-coupled atoms in a Zeeman lattice. Phys. Rev. Lett. 2018, 98, 061601. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, S.K.; Kartashov, Y.V.; Szameit, A.; Torner, L.; Konotop, V.V. Vector topological edge solitons in Floquet insulators. ACS Photonics 2020, 7, 735. [Google Scholar] [CrossRef]
- Peano, V.; Houde, M.; Marquardt, F.; Clerk, A.A. Topological Quantum Fluctuations and Traveling Wave Amplifiers. Phys. Rev. X 2016, 6, 041026. [Google Scholar] [CrossRef] [Green Version]
- Bardyn, C.E.; Karzig, T.; Refael, G.; Liew, T.C.H. Topological polaritons and excitons in garden-variety systems. Phys. Rev. B 2015, 91, 161413. [Google Scholar] [CrossRef] [Green Version]
- Bleu, O.; Solnyshkov, D.D.; Malpuech, G. Interacting quantum fluid in a polariton Chern insulator. Phys. Rev. B 2016, 93, 085438. [Google Scholar] [CrossRef] [Green Version]
- Flayac, H.; Shelykh, I.A.; Solnyshkov, D.D.; Malpuech, G. Topological stability of the half-vortices in spinor exciton-polariton condensates. Phys. Rev. B 2010, 81, 045318. [Google Scholar] [CrossRef] [Green Version]
- Plotnik, Y.; Rechtsman, M.; Song, D.; Heinrich, M.; Zeuner, J.; Nolte, S.; Lumer, Y.; Malkova, N.; Xu, J.; Szameit, A.; et al. Observation of unconventional edge states in ‘photonic graphene’. Nat. Mater. 2013, 13, 57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morimoto, T.; Nagaosa, N. Topological nature of nonlinear optical effects in solids. Sci. Adv. 2016, 2, e1501524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lumer, Y.; Plotnik, Y.; Rechtsman, M.C.; Segev, M. Self Localized States in Photonic Topological Insulators. Phys. Rev. Lett. 2013, 111, 243905. [Google Scholar] [CrossRef] [PubMed]
- Lumer, Y.; Rechtsman, M.C.; Plotnik, Y.; Segev, M. Instability of bosonic topological edge states inthe presence of interactions. Phys. Rev. A 2016, 94, 021801. [Google Scholar] [CrossRef] [Green Version]
- Hadad, Y.; Khanikaev, A.B.; Alù, A. Self-induced topological transitions and edge states supported by nonlinear staggered potentials. Phys. Rev. B 2016, 93, 155112. [Google Scholar] [CrossRef] [Green Version]
- Kartashov, Y.V.; Skryabin, D.V. Bistable Topological Insulator with Exciton-Polaritons. Phys. Rev. Lett. 2017, 119, 253904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharabi, Y.; Sheinfux, H.H.; Sagi, Y.; Eisenstein, G.; Segev, M. Self-Induced Diffusion in Disordered Nonlinear Photonic Media. Phys. Rev. Lett. 2018, 121, 233901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leykam, D.; Chong, Y.D. Edge Solitons in Nonlinear-Photonic Topological Insulators. Phys. Rev. Lett. 2016, 117, 143901. [Google Scholar] [CrossRef] [Green Version]
- Leggett, A.J. Bose-Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307. [Google Scholar] [CrossRef] [Green Version]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463. [Google Scholar] [CrossRef] [Green Version]
- Bernevig, B.A. Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haldane, F.D.M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef]
- Wu, B.; Niu, Q. Nonlinear Landau-Zener tunneling. Phys. Rev. A 2000, 61, 023402. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Zhao, W.; Zhou, L.; Gong, J. Nonlinear dirac cones. Phys. Rev. B 2017, 96, 121406. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wu, B.; Niu, Q. Nonlinear Evolution of Quantum States in the Adiabatic Regime. Phys. Rev. Lett. 2003, 90, 170404. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Fu, L.B.; Ou, B.Y.; Chen, S.G.; Choi, D.I.; Wu, B.; Niu, Q. Theory of nonlinear Landau-Zener tunneling. Phys. Rev. A 2002, 66, 023404. [Google Scholar] [CrossRef] [Green Version]
- Smirnova, D.; Smirnov, L.; Leykam, D.; Kivshar, Y. Topological Edge States and Gap Solitons in the Nonlinear Dirac Model. Laser Photon. Rev. 2019, 13, 1970053. [Google Scholar] [CrossRef]
- Jaksch, D.; Bruder, C.; Cirac, J.I.; Gardiner, C.W.; Zoller, P. Cold Bosonic Atoms in Optical Lattices. Phys. Rev. Lett. 1998, 81, 3108. [Google Scholar] [CrossRef]
- Cornish, S.L.; Claussen, N.R.; Roberts, J.L.; Cornell, E.A.; Wieman, C.E. Stable 85Rb Bose-Einstein Condensates with Widely Tunable Interactions. Phys. Rev. Lett. 2000, 85, 1795. [Google Scholar] [CrossRef] [Green Version]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 88. [Google Scholar] [CrossRef] [Green Version]
- Tarruell, L.; Greif, D.; Uehlinger, T.; Jotzu, G.; Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 2012, 483, 302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jotzu, G.; Messer, G.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237. [Google Scholar] [CrossRef] [Green Version]
- Wintersperger, K.; Braun, C.; Ünal, F.N.; Eckardt, A.; Liberto, M.D.; Goldman, N.; Bloch, I.; Aidelsburger, M. Realization of an anomalous Floquet topological system with ultracold atoms. Nat. Phys. 2020, 16, 1058. [Google Scholar] [CrossRef]
- Mishmash, R.V.; Carr, L.D. Ultracold atoms in 1D optical lattices: Mean field, quantum field, computation, and soliton formation, Mathematics and Computers in Simulation. Math. Comput. Simul. 2009, 80, 732. [Google Scholar] [CrossRef] [Green Version]
- Haddad, L.H.; Carr, L.D. The nonlinear Dirac equation in Bose-Einstein condensates: Foundation and symmetries. Physica D 2009, 238, 1413. [Google Scholar] [CrossRef] [Green Version]
- Pitaevskii, L.P. Vortex lines in an imperfect bose gas. Sov. Phys. JETP 1961, 13, 451. [Google Scholar]
- Tuloup, T.; Bomantara, R.W.; Lee, C.H.; Gong, J. Nonlinearity induced toological physics in momnetum space and real spance. Phys. Rev. B 2020, 102, 115411. [Google Scholar] [CrossRef]
- Kaiser, R.; Westbrook, C.; David, F. Coherent Atomic Matter Waves, 1st ed.; Spriner: Berlin/Heidelberg, Germany; New York, NY, USA; Barcelona, Spain; Hong Kong, China; London, UK; Milan, Italy; Paris, France; Singapore; Tokyo, Japan, 2001. [Google Scholar]
- Liu, J.; Fu, L.B. Berry phase in nonlinear systems. Phys. Rev. A 2010, 81, 052112. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45. [Google Scholar]
- Wilczek, F.; Shapere, A. Advanced Series in Mathematical Physics, Geometric Phases in Physics Volume 5; World Scientific: Singapore, 1989. [Google Scholar]
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. 1959, 115, 485. [Google Scholar] [CrossRef]
- Duca, L.; Li, T.; Reitter, M.; Bloch, I.; Schleier-Smith, M.; Schneider, U. An Aharonov-Bohm interferometer for determining Bloch band topology. Science 2015, 347, 288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.P.; Gui, Z.Q.; Chen, Y.Y. Nonlinear dynamics of a spin-orbit-coupled Bose-Einstein condensate. Phys. Rev. A 2019, 99, 023616. [Google Scholar] [CrossRef] [Green Version]
- Jin, J.S.; Rossini, D.; Fazio, R. Photon solid phases in driven arrays of nonlinearly coupled cavities. Phys. Rev. Lett. 2013, 110, 163605. [Google Scholar] [CrossRef] [PubMed]
- Kounalakis, M.; Dickel, C.; Bruno, A.; Langford, N.K.; Steele, G.A. Tuneable hopping and nonlinear cross-Kerr interactions in a high-coherence superconducting circuit. NPJ Quantum Inf. 2018, 4, 38. [Google Scholar] [CrossRef]
- Hartmann, M.; Brandão, F.; Plenio, M. Quantum many-body phenomena in coupled cavity arrays. Laser Photon. Rev. 2008, 2, 527. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Xue, K.; Yi, X. Nonlinear Topological Effects in Optical Coupled Hexagonal Lattice. Entropy 2021, 23, 1404. https://doi.org/10.3390/e23111404
Li F, Xue K, Yi X. Nonlinear Topological Effects in Optical Coupled Hexagonal Lattice. Entropy. 2021; 23(11):1404. https://doi.org/10.3390/e23111404
Chicago/Turabian StyleLi, Fude, Kang Xue, and Xuexi Yi. 2021. "Nonlinear Topological Effects in Optical Coupled Hexagonal Lattice" Entropy 23, no. 11: 1404. https://doi.org/10.3390/e23111404





