Detection of Mutual Exciting Structure in Stock Price Trend Dynamics
Abstract
:1. Introduction
2. Materials and Methods
2.1. DATA
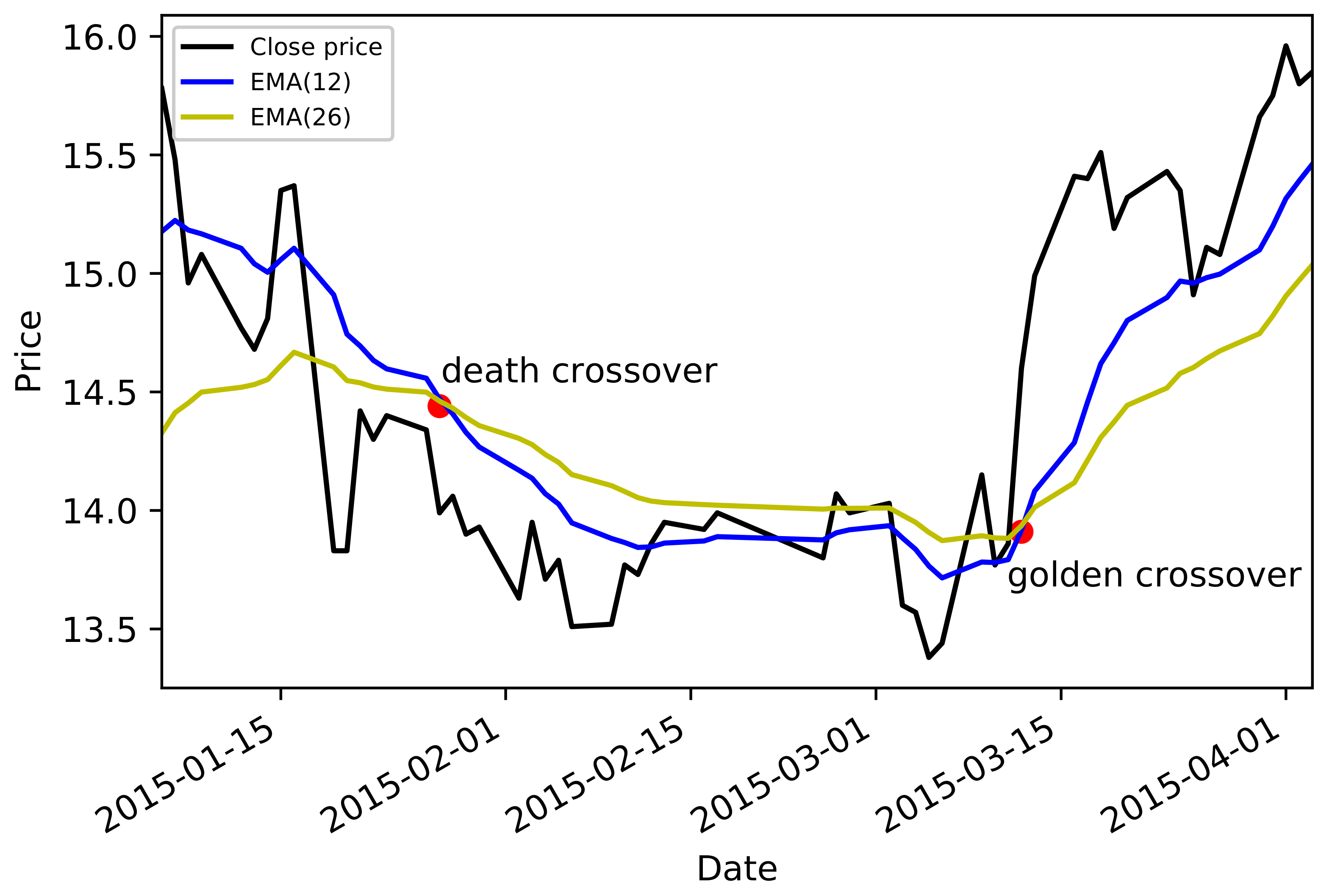
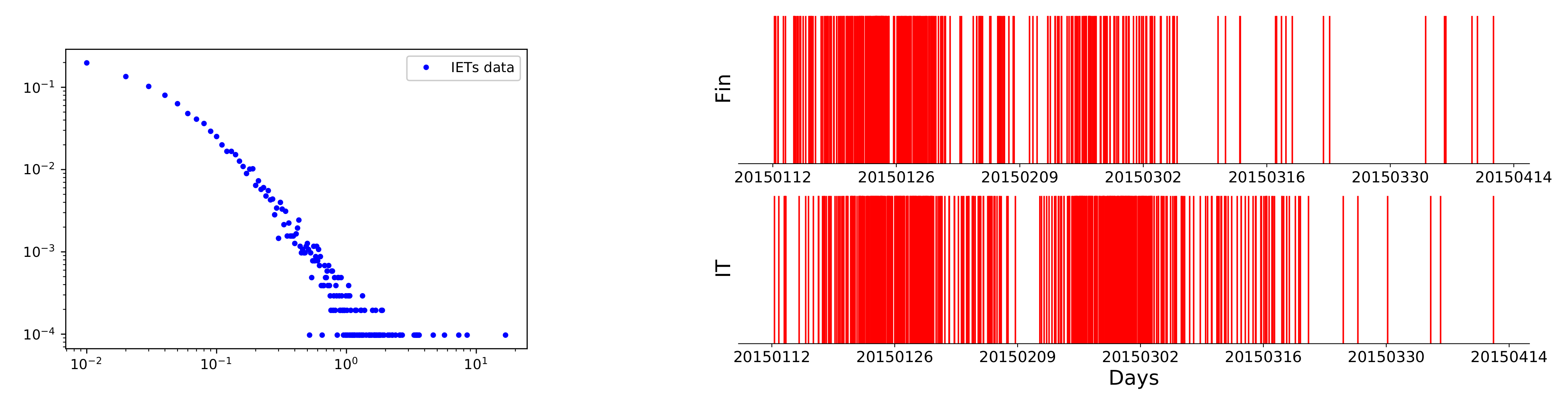
2.2. Statistical Measure for Crossover Event Sequences
2.3. The Univariate Hawkes Processes
2.4. The Mutual and Multidimensional Hawkes Processes
3. Results and Discussion
3.1. Single Sector
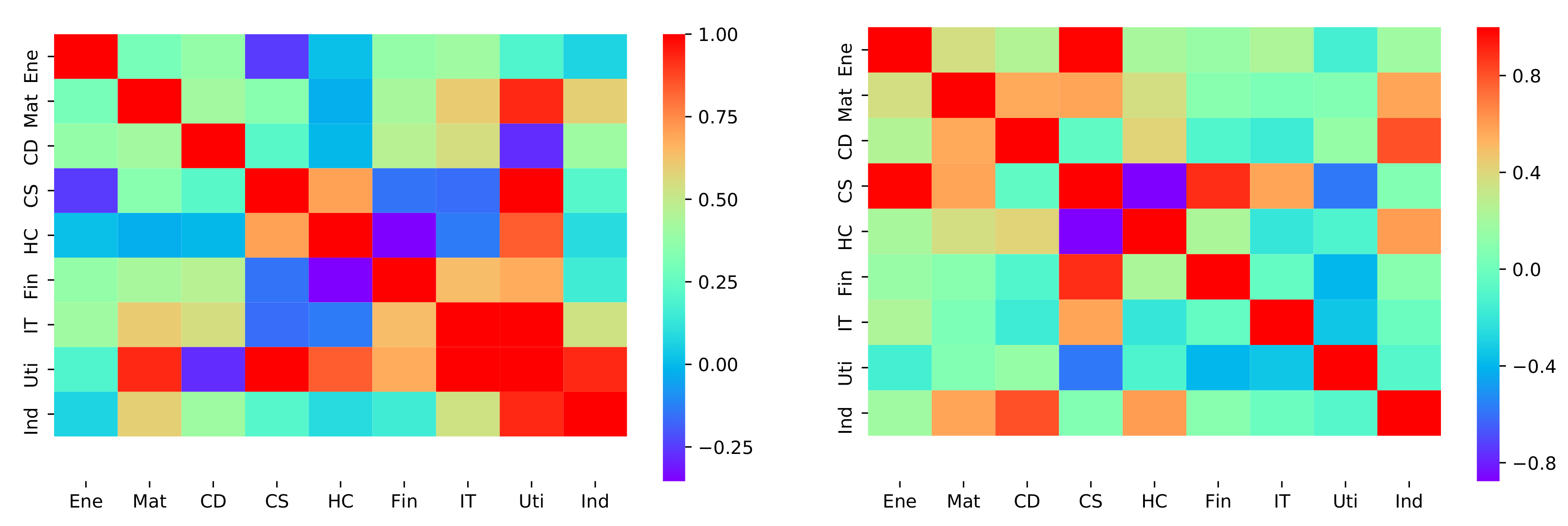
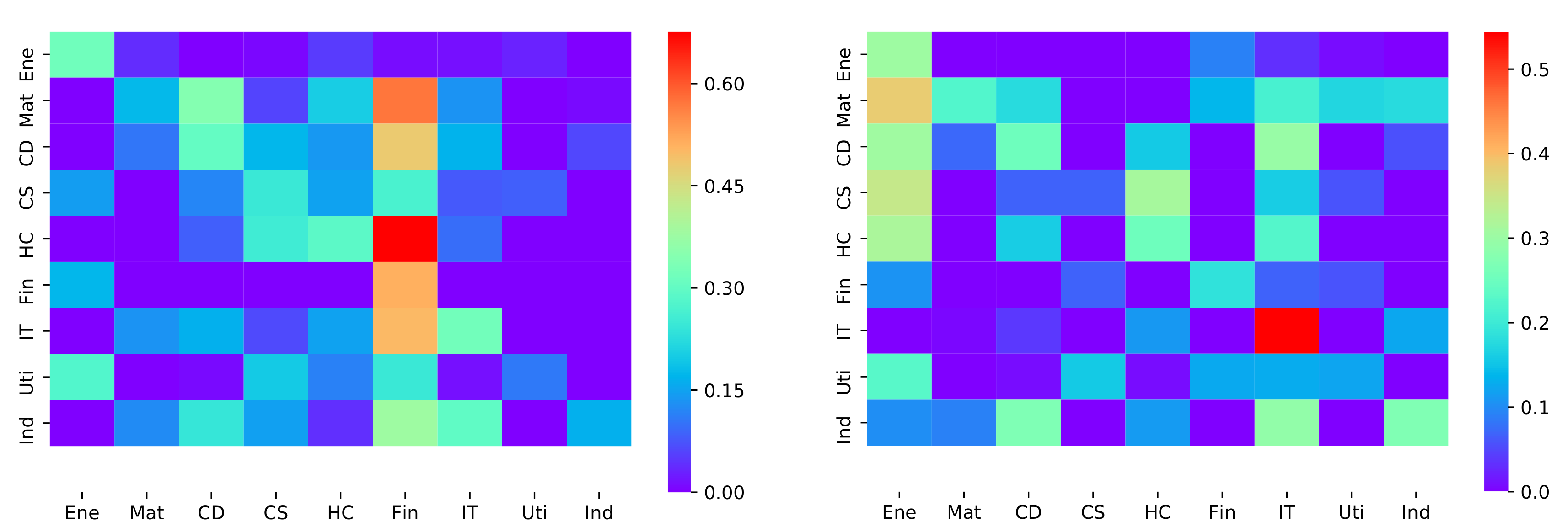
3.2. Multiple Sectors
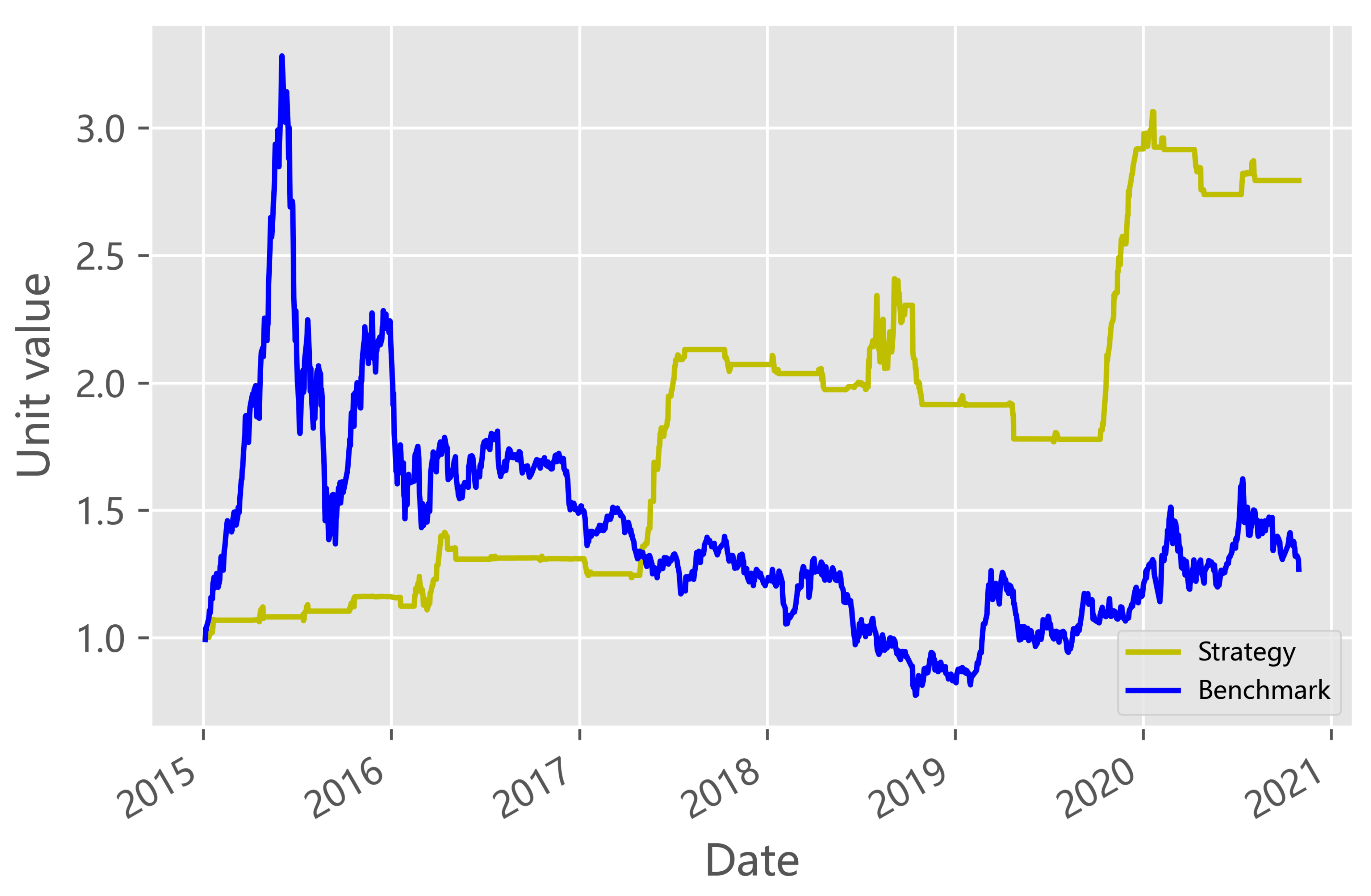
3.3. Strategy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hawkes, A. Cluster models for earthquakes-regional comparisons. Bull. Int. Stat. Inst. 1973, 45, 454–461. [Google Scholar]
- Ogata, Y. The asymptotic behaviour of maximum likelihood estimators for stationary point processes. Ann. Inst. Stat. Math. 1978, 30, 243–261. [Google Scholar] [CrossRef]
- Su, J.B. How to Promote the Performance of Parametric Volatility Forecasts in the Stock Market? A Neural Networks Approach. Entropy 2021, 23, 1151. [Google Scholar] [CrossRef] [PubMed]
- Yen, P.T.W.; Xia, K.; Cheong, S.A. Understanding Changes in the Topology and Geometry of Financial Market Correlations during a Market Crash. Entropy 2021, 23, 1211. [Google Scholar] [CrossRef] [PubMed]
- Fujita, K.; Medvedev, A.; Koyama, S.; Lambiotte, R.; Shinomoto, S. Identifying exogenous and endogenous activity in social media. Phys. Rev. E 2018, 98, 052304. [Google Scholar] [CrossRef] [Green Version]
- Krumin, M.; Reutsky, I.; Shoham, S. Correlation-based analysis and generation of multiple spike trains using Hawkes models with an exogenous input. Front. Comput. Neurosci. 2010, 4, 147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pernice, V.; Rotter, S. Reconstruction of sparse connectivity in neural networks from spike train covariances. J. Stat. Mech. Theory Exp. 2013, 2013, P03008. [Google Scholar] [CrossRef]
- Rambaldi, M.; Filimonov, V.; Lillo, F. Detection of intensity bursts using Hawkes processes: An application to high-frequency financial data. Phys. Rev. E 2018, 97, 032318. [Google Scholar] [CrossRef] [Green Version]
- Bacry, E.; Muzy, J.F. Hawkes model for price and trades high-frequency dynamics. Quant. Financ. 2014, 14, 1147–1166. [Google Scholar] [CrossRef] [Green Version]
- Bacry, E.; Delattre, S.; Hoffmann, M.; Muzy, J.F. Modeling microstructure noise with mutually exciting point processes. Quant. Financ. 2013, 13, 65–77. [Google Scholar] [CrossRef]
- Bacry, E.; Jaisson, T.; Muzy, J.F. Estimation of slowly decreasing hawkes kernels: Application to high-frequency order book dynamics. Quant. Financ. 2016, 16, 1179–1201. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Y.; Li, F. Feature Extraction of Sequence of Keystrokes in Fixed Text Using the Multivariate Hawkes Process. Math. Probl. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Rambaldi, M.; Pennesi, P.; Lillo, F. Modeling foreign exchange market activity around macroeconomic news: Hawkes-process approach. Phys. Rev. E 2015, 91, 012819. [Google Scholar] [CrossRef] [Green Version]
- Xia, L.; You, D.; Jiang, X.; Guo, Q. Comparison between global financial crisis and local stock disaster on top of Chinese stock network. Phys. Stat. Mech. Its Appl. 2018, 490, 222–230. [Google Scholar] [CrossRef]
- Hawkes, A.G. Point spectra of some mutually exciting point processes. J. R. Stat. Soc. Ser. (Methodol.) 1971, 33, 438–443. [Google Scholar] [CrossRef]
- Hawkes, A.G. Spectra of some self-exciting and mutually exciting point processes. Biometrika 1971, 58, 83–90. [Google Scholar] [CrossRef]
- Bauwens, L.; Hautsch, N. Modelling financial high frequency data using point processes. In Handbook of Financial Time Series; Springer: Berlin/Heidelberg, Germany, 2009; pp. 953–979. [Google Scholar]
- Omi, T.; Hirata, Y.; Aihara, K. Hawkes process model with a time-dependent background rate and its application to high-frequency financial data. Phys. Rev. E 2017, 96, 012303. [Google Scholar] [CrossRef] [Green Version]
- Bowsher, C.G. Modelling security market events in continuous time: Intensity based, multivariate point process models. J. Econom. 2007, 141, 876–912. [Google Scholar] [CrossRef] [Green Version]
- Hardiman. Branching-ratio approximation for the self-exciting Hawkes process. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2014, 90, 062807. [Google Scholar] [CrossRef] [Green Version]
- Filimonov, V.; Sornette, D. Quantifying reflexivity in financial markets: Toward a prediction of flash crashes. Phys. Rev. E 2012, 85, 056108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Embrechts, P.; Liniger, T.; Lin, L. Multivariate Hawkes Processes: An Application to Financial Data. J. Appl. Probab. 2011, 48, 367–378. [Google Scholar] [CrossRef] [Green Version]
- Jaisson, T.; Rosenbaum, M. Limit theorems for nearly unstable Hawkes processes. Ann. Appl. Probab. 2015, 25, 600–631. [Google Scholar] [CrossRef] [Green Version]
- Bacry, E.; Iuga, A.; Lasnier, M.; Lehalle, C.A. Market impacts and the life cycle of investors orders. Mark. Microstruct. Liq. 2015, 1, 1550009. [Google Scholar] [CrossRef]
- Hawkes, A.G. Hawkes processes and their applications to finance: A review. Quant. Financ. 2018, 18, 193–198. [Google Scholar] [CrossRef]
- Bacry, E.; Mastromatteo, I.; Muzy, J.F. Hawkes processes in finance. Mark. Microstruct. Liq. 2015, 1, 1550005. [Google Scholar] [CrossRef]
- At-Sahalia, Y.; Cacho-Diaz, J.; Laeven, R.J. Modeling financial contagion using mutually exciting jump processes. J. Financ. Econ. 2015, 117, 585–606. [Google Scholar] [CrossRef] [Green Version]
- Diep, H.T.; Desgranges, G. Dynamics of the price behavior in stock markets: A statistical physics approach. Phys. Stat. Mech. Its Appl. 2021, 570, 125813. [Google Scholar] [CrossRef]
- Pätäri, E.; Vilska, M. Performance of moving average trading strategies over varying stock market conditions: The Finnish evidence. Appl. Econ. 2014, 46, 2851–2872. [Google Scholar] [CrossRef]
- Shynkevich, A. Performance of technical analysis in growth and small cap segments of the US equity market. J. Bank. Financ. 2012, 36, 193–208. [Google Scholar] [CrossRef]
- Park, C.; Irwin, S.H. What do we know about the profitability of technical analysis? J. Econ. Surv. 2007, 21, 786–826. [Google Scholar] [CrossRef]
- Brock, W.; Lakonishok, J.; Lebaron, B. Simple Technical Trading Rules and the Stochastic Properties of Stock Returns. J. Financ. 1992, 47, 1731–1764. [Google Scholar] [CrossRef]
- Sullivan, R.; Timmermann, A.; White, H. Data-snooping, technical trading rule performance, and the bootstrap. J. Financ. 1999, 54, 1647–1691. [Google Scholar] [CrossRef]
- Toke, I.M. “Market Making” in an Order Book Model and Its Impact on the Spread. New Econ. Wind. 2011, 9, 49–64. [Google Scholar]
- Heeger, D. Poisson model of spike generation. Handout Univ. Standford 2000, 5, 1–13. [Google Scholar]
- Shinomoto, S.; Shima, K.; Tanji, J. Differences in spiking patterns among cortical neurons. Neural Comput. 2003, 15, 2823–2842. [Google Scholar] [CrossRef]
- Shinomoto, S.; Kim, H.; Shimokawa, T.; Matsuno, N.; Funahashi, S.; Shima, K.; Fujita, I.; Tamura, H.; Doi, T.; Kawano, K.; et al. Relating neuronal firing patterns to functional differentiation of cerebral cortex. PLoS Comput. Biol. 2009, 5, e1000433. [Google Scholar] [CrossRef]
- Aoki, T.; Takaguchi, T.; Kobayashi, R.; Lambiotte, R. Input-output relationship in social communications characterized by spike train analysis. Phys. Rev. E 2016, 94, 042313. [Google Scholar] [CrossRef] [Green Version]
- Sanlı, C.; Lambiotte, R. Local variation of hashtag spike trains and popularity in twitter. PLoS ONE 2015, 10, e0131704. [Google Scholar] [CrossRef]
- Abdullah, M. The implication of machine learning for financial solvency prediction: An empirical analysis on public listed companies of Bangladesh. J. Asian Bus. Econ. Stud. 2021. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z. Forecasting stock price movement: New evidence from a novel hybrid deep learning model. J. Asian Bus. Econ. Stud. 2021. [Google Scholar] [CrossRef]



| Sectors | Ene | Mat | CD | CS | HC | Fin | IT | Tel | Uti | Ind |
|---|---|---|---|---|---|---|---|---|---|---|
| No. of stocks | 83 | 618 | 596 | 214 | 293 | 98 | 668 | 4 | 121 | 924 |
| No. of golden crossovers | 847 | 5641 | 5274 | 2244 | 2813 | 978 | 5648 | 40 | 1384 | 8463 |
| No. of death crossovers | 812 | 5355 | 5011 | 2148 | 2671 | 920 | 5388 | 39 | 1354 | 8164 |
| Avg. interval of golden crossover | 13.9 | 12.8 | 11.6 | 12.4 | 12.8 | 11.1 | 12 | 37.4 | 11.4 | 10.1 |
| Avg. interval of death crossover | 14.2 | 13.8 | 12.6 | 13.4 | 13.4 | 11 | 12.5 | 36.9 | 11.2 | 12.9 |
| Ene | Mat | CD | CS | HC | Fin | IT | Uti | Ind |
|---|---|---|---|---|---|---|---|---|
| 2.3734 | 2.8053 | 2.6929 | 3.0038 | 2.6672 | 2.0956 | 2.7666 | 2.3319 | 2.5408 |
| Golden Crossover | |||||||||
| Sectors | Ene | Mat | CD | CS | HC | Fin | IT | Uti | Ind |
| 0.317 | 1.509 | 1.252 | 0.700 | 0.709 | 0.303 | 1.498 | 0.495 | 2.092 | |
| 0.512 | 0.609 | 0.709 | 0.667 | 0.720 | 0.595 | 0.661 | 0.590 | 0.619 | |
| 0.544 | 0.707 | 0.712 | 0.692 | 0.730 | 0.634 | 0.696 | 0.607 | 0.632 | |
| n | 0.941 | 0.861 | 0.996 | 0.964 | 0.986 | 0.938 | 0.950 | 0.972 | 0.979 |
| Death Crossover | |||||||||
| Sectors | Ene | Mat | CD | CS | HC | Fin | IT | Uti | Ind |
| 0.349 | 1.328 | 1.371 | 0.728 | 0.847 | 0.323 | 1.274 | 0.626 | 1.858 | |
| 0.351 | 0.648 | 0.616 | 0.614 | 0.614 | 0.469 | 0.679 | 0.492 | 0.631 | |
| 0.366 | 0.649 | 0.669 | 0.637 | 0.653 | 0.482 | 0.711 | 0.516 | 0.666 | |
| n | 0.959 | 0.998 | 0.921 | 0.963 | 0.940 | 0.973 | 0.955 | 0.953 | 0.947 |
| Golden Crossover | |||||||||
| Sectors | Ene | Mat | CD | CS | HC | Fin | IT | Uti | Ind |
| Activity (events/day) | 0.741 | 4.897 | 4.559 | 1.927 | 2.388 | 0.834 | 4.833 | 1.204 | 7.317 |
| 0.029 | 0.69 | 0.428 | 0.013 | 0.001 | 0.232 | 0.858 | 0 | 2.092 | |
| Single | 0.317 | 1.509 | 1.252 | 0.7 | 0.709 | 0.303 | 1.498 | 0.495 | 2.092 |
| Death Crossover | |||||||||
| Sectors | Ene | Mat | CD | CS | HC | Fin | IT | Uti | Ind |
| Activity (events/day) | 0.726 | 4.692 | 4.369 | 1.868 | 2.273 | 0.791 | 4.617 | 1.195 | 7.14 |
| 0.165 | 0.208 | 0.52 | 0.193 | 0.342 | 0.032 | 0.686 | 0.019 | 0.77 | |
| Single | 0.349 | 1.328 | 1.371 | 0.728 | 0.847 | 0.323 | 1.274 | 0.626 | 1.858 |
| Sectors | Ene | Mat | CD | CS | HC | Fin | IT | Uti | Ind |
|---|---|---|---|---|---|---|---|---|---|
| Golden case mean | 0.101 | 0.064 | 0.141 | 0.128 | 0.126 | 0.405 | 0.125 | 0.025 | 0.026 |
| Death case mean | 0.234 | 0.044 | 0.11 | 0.033 | 0.107 | 0.061 | 0.219 | 0.047 | 0.07 |
| Signal | Operation |
|---|---|
| The number of golden EMA crossovers of the leading sector within one day exceeds a certain threshold | Buy stocks without any EMA golden crossovers when the signal arrives |
| The number of death EMA crossovers of the leading sector within one day exceeds a certain threshold | Sell stocks in long position without any EMA death crossovers when the signal arrives |
| MACD of the stock in long position is smaller than 0 | Sell the corresponding stock |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Jiang, X.; Wu, J.; Tong, L.; Xu, K. Detection of Mutual Exciting Structure in Stock Price Trend Dynamics. Entropy 2021, 23, 1411. https://doi.org/10.3390/e23111411
Li S, Jiang X, Wu J, Tong L, Xu K. Detection of Mutual Exciting Structure in Stock Price Trend Dynamics. Entropy. 2021; 23(11):1411. https://doi.org/10.3390/e23111411
Chicago/Turabian StyleLi, Shangzhe, Xin Jiang, Junran Wu, Lin Tong, and Ke Xu. 2021. "Detection of Mutual Exciting Structure in Stock Price Trend Dynamics" Entropy 23, no. 11: 1411. https://doi.org/10.3390/e23111411
APA StyleLi, S., Jiang, X., Wu, J., Tong, L., & Xu, K. (2021). Detection of Mutual Exciting Structure in Stock Price Trend Dynamics. Entropy, 23(11), 1411. https://doi.org/10.3390/e23111411






