Algorithmic Approaches for Assessing Irreversibility in Time Series: Review and Comparison
Abstract
1. Introduction
1.1. Applications
1.2. Assessing Irreversibility in Real-World Time Series
2. Numerical Methods
2.1. The BDS Statistic
2.2. Ramsey and Rothman’s Time Reversibility Test
2.3. The DFK Test
2.4. Permutation Patterns (Permp) Test
2.5. The Ternary Coding (TC) Test
2.6. Micro-Scale Trends (MSTrends) Test
2.7. Visibility Graphs
2.8. Local Clustering Coefficient
2.9. Additional Irreversibility Tests
3. Evaluation and Comparison
3.1. Preliminaries
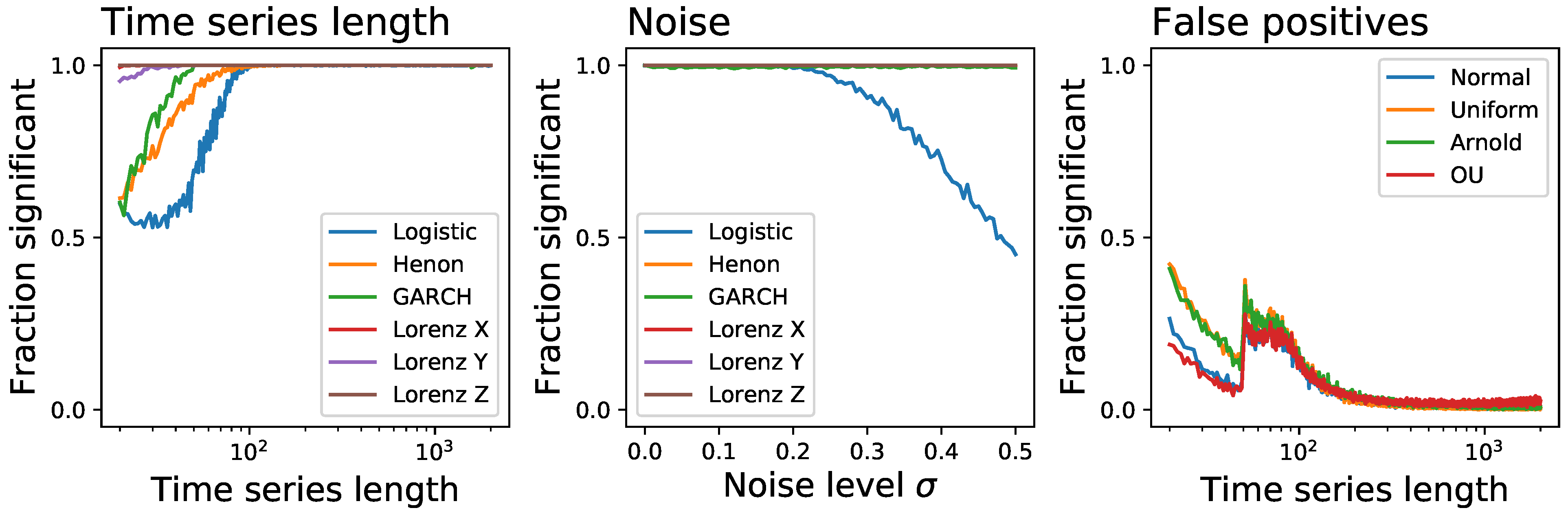
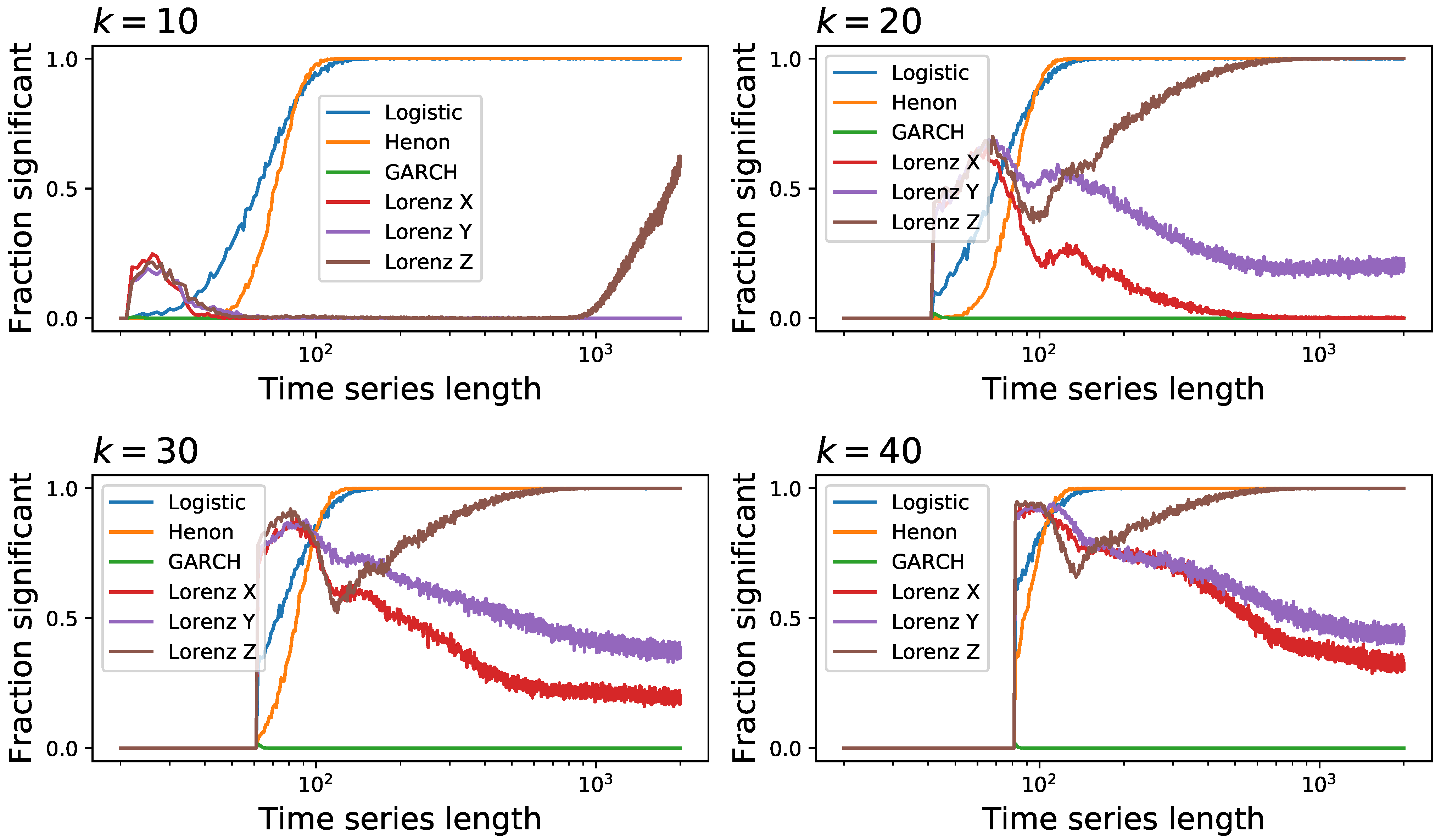
3.2. Tests’ Performance on Synthetic Data
- the previously defined logistic map , with , and without observational noise;
- the Henon map, defined as , , with and ;
- the Generalised Autoregressive Conditional Heteroskedasticity (GARCH) model [85], defined as , with , , and being independent random numbers drawn from an uniform distribution ; and
- the three variables of the Lorenz chaotic system, a continuos system defined as , , and , with , and .
- time series composed of random number extracted from a normal distribution ;
- time series composed of random number extracted from a uniform distribution ;
- the x variable of the Arnold Cat map, a conservative (and hence reversible) chaotic map defined as: , .
- the Ornstein-Uhlenbeck process, i.e., a mean-reverting linear Gaussian process T [1].
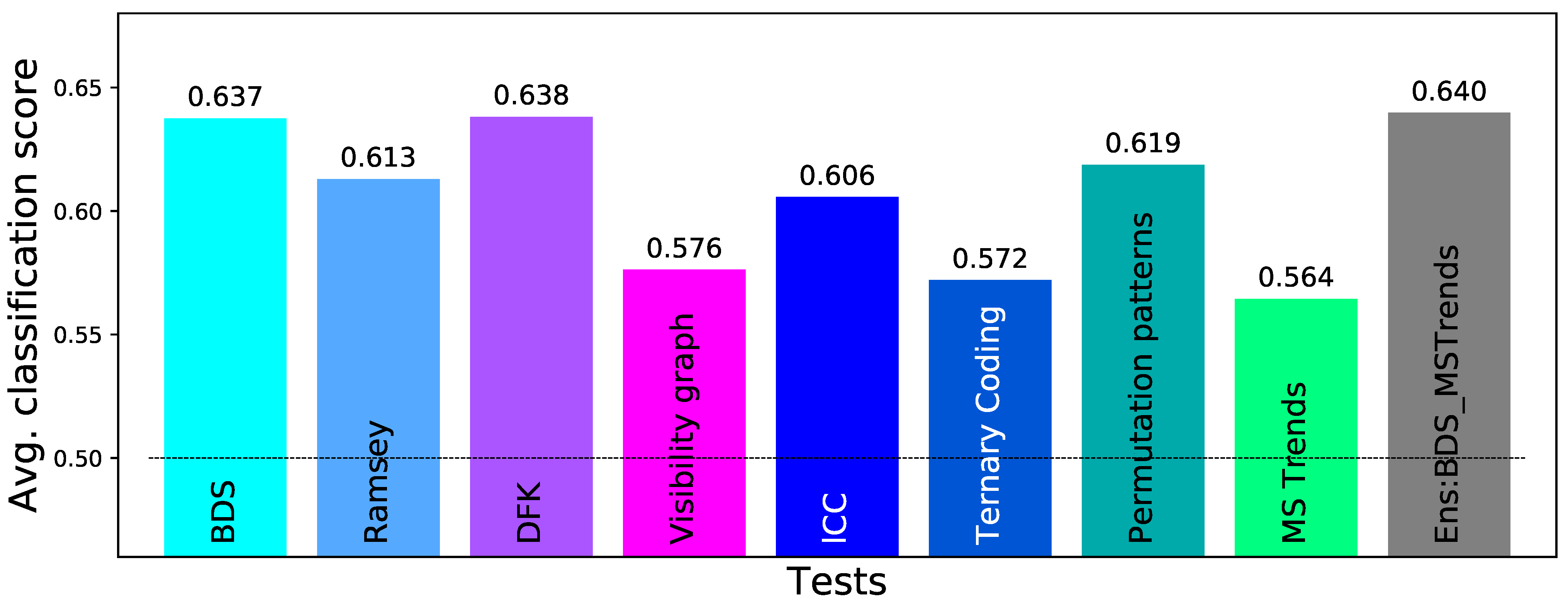
3.3. Ensemble Testing
- Combining all eight tests into a single one (here denoted by Ens:all).
- Combine the two most effective tests, i.e., BDS and MSTrends (Ens:BDS_MSTrends).
- Combine the pairs of tests that yield the most independent results, such that the errors of one of them could be corrected by the other. These pairs would be Ramsey and PermP (Ens:Ramsey_PermP), and lCC and MSTrends (Ens:lCC_MSTrends).
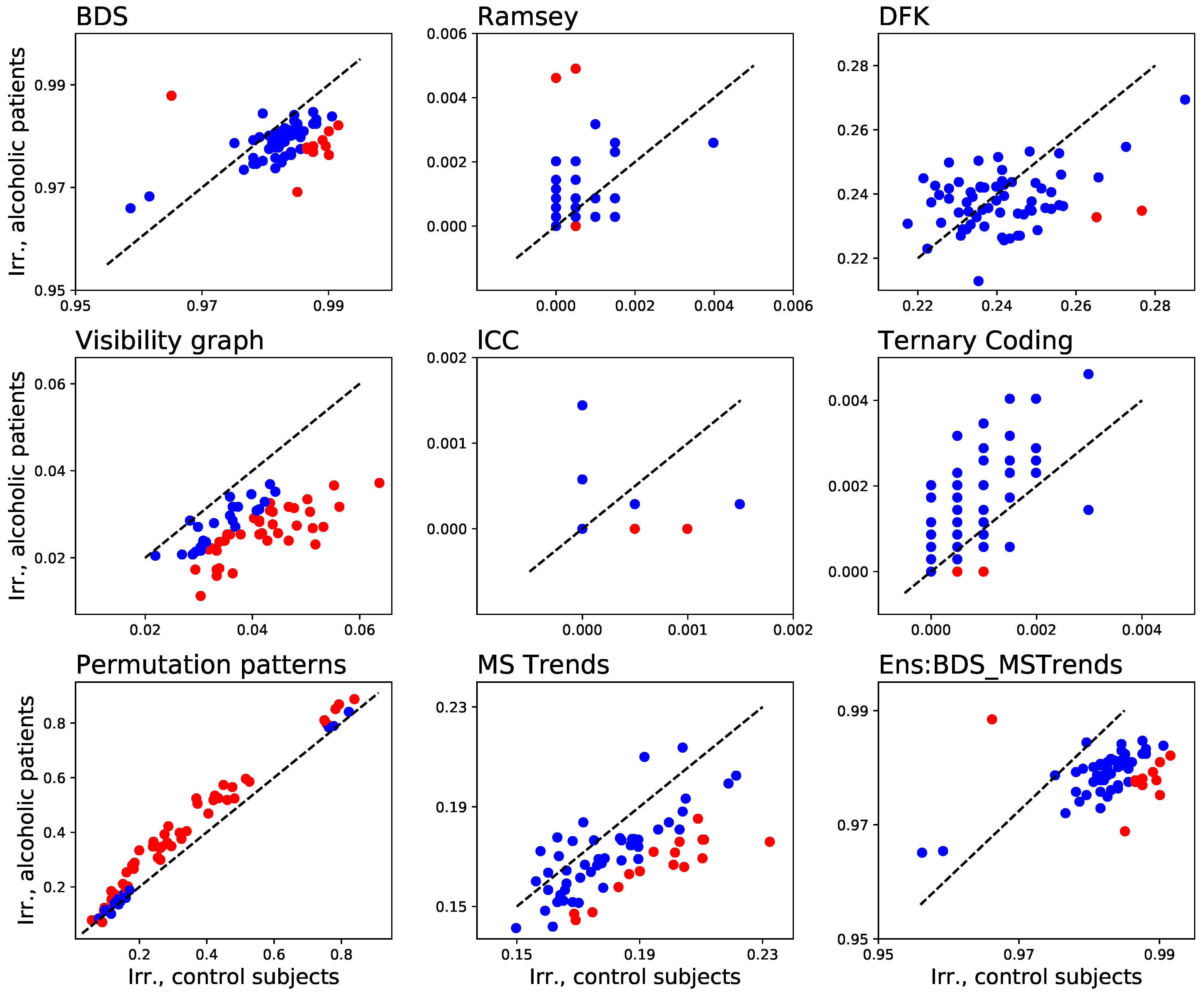
3.4. Analysing Real-World Data: The Case of Human Electro-Encephalography
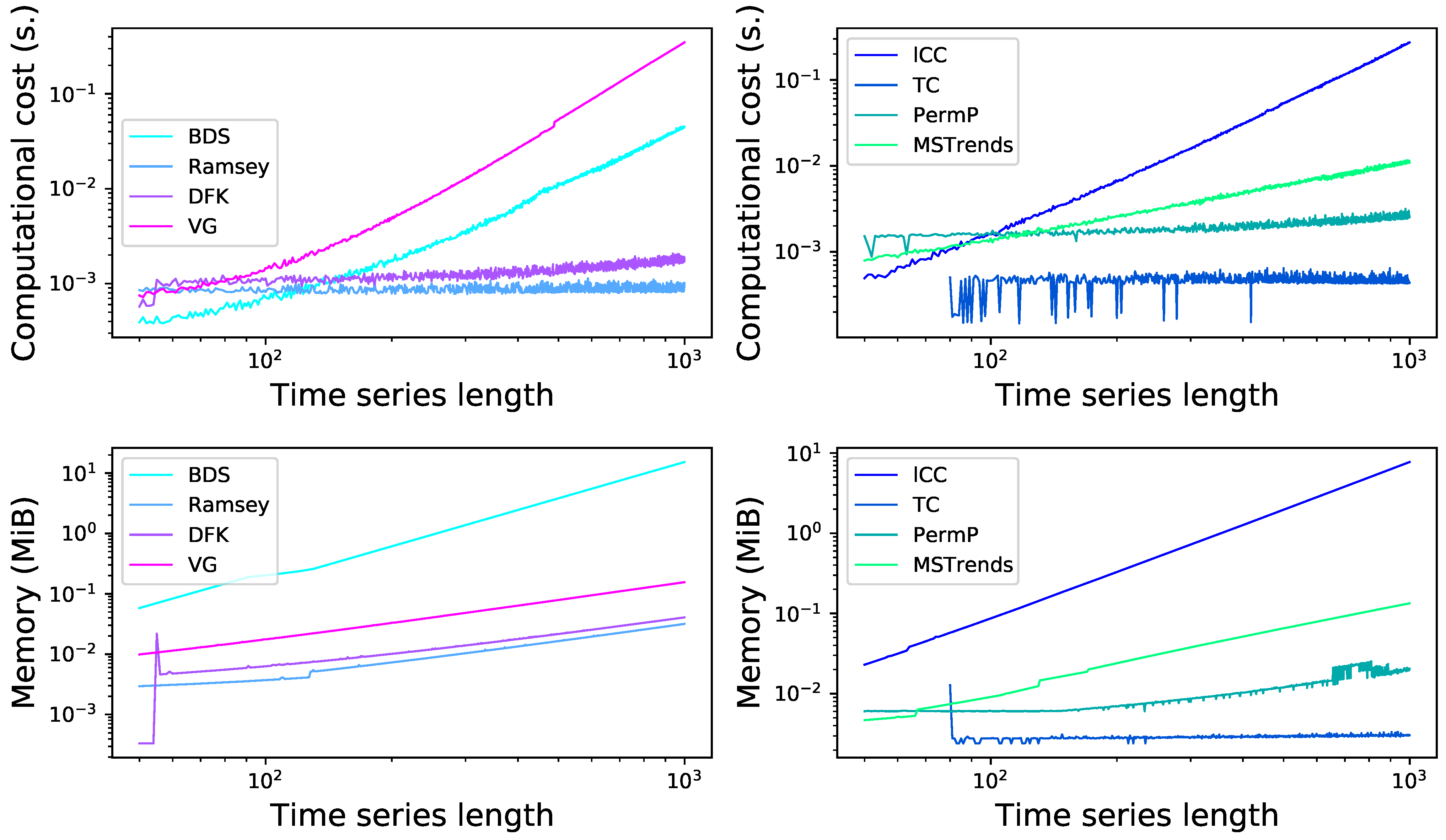
3.5. Computational Cost
4. Software
- Tests are organised in independent modules, whose names are reported in Table 2. Each test has a main function, always called GetPValue, which returns two results: the p-value of the test, and the statistic of the test when available. Besides the time series to be analysed, each test expects a set of parameters, which are also described in Table 2.
- Some tests include simplifications in their execution; to illustrate, the permutation patterns algorithm only considers patterns of size 3; and the micro-scale trends one only linear regressions of the data. The reader should nevertheless note that this will be a live library, and that such simplifications may disappear in the future. We therefore recommend to check the online documentation of the project.
- In order to simplify the use of the library, it includes an example program UsageExample.py, which creates a time series using a logistic map, and sequentially executes all available tests with different parameters. We recommend the interested reader to start by checking this program.
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Weiss, G. Time-reversibility of linear stochastic processes. J. Appl. Probab. 1975, 12, 831–836. [Google Scholar] [CrossRef]
- Cox, D.R.; Gudmundsson, G.; Lindgren, G.; Bondesson, L.; Harsaae, E.; Laake, P.; Juselius, K.; Lauritzen, S.L. Stat. Anal. Time Ser. Some Recent Dev. [with discussion and reply]. Scand. J. Stat. 1981, 8, 93–115. [Google Scholar]
- Lawrance, A. Directionality and reversibility in time series. Int. Stat. Rev./Revue Internationale de Statistique 1991, 59, 67–79. [Google Scholar] [CrossRef]
- Stone, L.; Landan, G.; May, R.M. Detecting time’s arrow: A method for identifying nonlinearity and deterministic chaos in time-series data. Proc. R. Soc. Lond. 1996, 263, 1509–1513. [Google Scholar]
- Pomeau, Y. Symétrie des fluctuations dans le renversement du temps. J. Phys. 1982, 43, 859–867. [Google Scholar] [CrossRef]
- Puglisi, A.; Villamaina, D. Irreversible effects of memory. Europhys. Lett. 2009, 88, 30004. [Google Scholar] [CrossRef]
- Porporato, A.; Rigby, J.R.; Daly, E. Irreversibility and fluctuation theorem in stationary time series. Phys. Rev. Lett. 2007, 98, 094101. [Google Scholar] [CrossRef]
- Xia, J.; Shang, P.; Wang, J.; Shi, W. Classifying of financial time series based on multiscale entropy and multiscale time irreversibility. Phys. A Stat. Mech. Its Appl. 2014, 400, 151–158. [Google Scholar] [CrossRef]
- Maes, C.; Netočnỳ, K. Time-reversal and entropy. J. Stat. Phys. 2003, 110, 269–310. [Google Scholar] [CrossRef]
- Gnesotto, F.S.; Mura, F.; Gladrow, J.; Broedersz, C.P. Broken detailed balance and non-equilibrium dynamics in living systems: A review. Rep. Prog. Phys. 2018, 81, 066601. [Google Scholar] [CrossRef]
- Gaspard, P. Time-reversed dynamical entropy and irreversibility in Markovian random processes. J. Stat. Phys. 2004, 117, 599–615. [Google Scholar] [CrossRef]
- Parrondo, J.M.; Van den Broeck, C.; Kawai, R. Entropy production and the arrow of time. New J. Phys. 2009, 11, 073008. [Google Scholar] [CrossRef]
- Roldán, É.; Martinez, I.A.; Parrondo, J.M.; Petrov, D. Universal features in the energetics of symmetry breaking. Nat. Phys. 2014, 10, 457–461. [Google Scholar] [CrossRef]
- Fodor, É.; Nardini, C.; Cates, M.E.; Tailleur, J.; Visco, P.; van Wijland, F. How far from equilibrium is active matter? Phys. Rev. Lett. 2016, 117, 038103. [Google Scholar] [CrossRef]
- Battle, C.; Broedersz, C.P.; Fakhri, N.; Geyer, V.F.; Howard, J.; Schmidt, C.F.; MacKintosh, F.C. Broken detailed balance at mesoscopic scales in active biological systems. Science 2016, 352, 604–607. [Google Scholar] [CrossRef] [PubMed]
- Gaspard, P. Brownian motion, dynamical randomness and irreversibility. New J. Phys. 2005, 7, 77. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P.; Ciliberto, S.; Garnier, N.; Joubaud, S.; Petrosyan, A. Entropy production and time asymmetry in nonequilibrium fluctuations. Phys. Rev. Lett. 2007, 98, 150601. [Google Scholar] [CrossRef]
- Kawai, R.; Parrondo, J.M.; Van den Broeck, C. Dissipation: The phase-space perspective. Phys. Rev. Lett. 2007, 98, 080602. [Google Scholar] [CrossRef]
- Andrieux, D.; Gaspard, P. Dynamical randomness, information, and Landauer’s principle. Europhys. Lett. 2007, 81, 28004. [Google Scholar] [CrossRef][Green Version]
- Esposito, M.; Van den Broeck, C. Second law and Landauer principle far from equilibrium. Europhys. Lett. 2011, 95, 40004. [Google Scholar] [CrossRef]
- Roldán, É.; Parrondo, J.M. Estimating dissipation from single stationary trajectories. Phys. Rev. Lett. 2010, 105, 150607. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.; Skordas, E.; Sarlis, N. Fluctuations of the entropy change under time reversal: Further investigations on identifying the occurrence time of an impending major earthquake. Europhys. Lett. 2020, 130, 29001. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time: Precursory Seismic Electric Signals, Earthquakes and Other Complex Time Series; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sarlis, N.; Skordas, E.; Varotsos, P. Order parameter fluctuations of seismicity in natural time before and after mainshocks. Europhys. Lett. 2010, 91, 59001. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. Space Phys. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Sarlis, N.V. Entropy in natural time and the associated complexity measures. Entropy 2017, 19, 177. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Nagao, T.; Kamogawa, M.; Uyeda, S. Spatiotemporal variations of seismicity before major earthquakes in the Japanese area and their relation with the epicentral locations. Proc. Natl. Acad. Sci. USA 2015, 112, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Martin, P.; Hudspeth, A.; Jülicher, F. Comparison of a hair bundle’s spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process. Proc. Natl. Acad. Sci. USA 2001, 98, 14380–14385. [Google Scholar] [CrossRef]
- Mizuno, D.; Tardin, C.; Schmidt, C.F.; MacKintosh, F.C. Nonequilibrium mechanics of active cytoskeletal networks. Science 2007, 315, 370–373. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation–dissipation: Response theory in statistical physics. Phys. Rep. 2008, 461, 111–195. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Harada, T.; Sasa, S.i. Equality connecting energy dissipation with a violation of the fluctuation-response relation. Phys. Rev. Lett. 2005, 95, 130602. [Google Scholar] [CrossRef] [PubMed]
- Cugliandolo, L.F. The effective temperature. J. Phys. Math. Theor. 2011, 44, 483001. [Google Scholar] [CrossRef]
- Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of second law violations in shearing steady states. Phys. Rev. Lett. 1993, 71, 2401. [Google Scholar] [CrossRef]
- Gallavotti, G.; Cohen, E.G.D. Dynamical ensembles in nonequilibrium statistical mechanics. Phys. Rev. Lett. 1995, 74, 2694. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. The fluctuation theorem. Adv. Phys. 2002, 51, 1529–1585. [Google Scholar] [CrossRef]
- Lecomte, V.; Appert-Rolland, C.; Van Wijland, F. Thermodynamic formalism for systems with Markov dynamics. J. Stat. Phys. 2007, 127, 51–106. [Google Scholar] [CrossRef]
- Sekimoto, K. Stochastic Energetics; Springer: Berlin, Germany, 2010; Volume 799. [Google Scholar]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Barato, A.C.; Seifert, U. Thermodynamic uncertainty relation for biomolecular processes. Phys. Rev. Lett. 2015, 114, 158101. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Gingrich, T.R. Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nat. Phys. 2020, 16, 15–20. [Google Scholar] [CrossRef]
- Falasco, G.; Esposito, M. Dissipation-time uncertainty relation. Phys. Rev. Lett. 2020, 125, 120604. [Google Scholar] [CrossRef]
- Shiraishi, N.; Funo, K.; Saito, K. Speed limit for classical stochastic processes. Phys. Rev. Lett. 2018, 121, 070601. [Google Scholar] [CrossRef]
- Falasco, G.; Esposito, M. Local detailed balance across scales: From diffusions to jump processes and beyond. Phys. Rev. E 2021, 103, 042114. [Google Scholar] [CrossRef] [PubMed]
- Pumir, A. Statistical properties of an equation describing fluid interfaces. J. Phys. 1985, 46, 511–522. [Google Scholar] [CrossRef]
- Arneodo, A.; Muzy, J.F.; Sornette, D. “Direct” causal cascade in the stock market. Eur. Phys. J. B 1998, 2, 277–282. [Google Scholar] [CrossRef]
- Ramsey, J.B.; Rothman, P. Time irreversibility and business cycle asymmetry. J. Money, Credit. Bank. 1996, 28, 1–21. [Google Scholar] [CrossRef]
- Zumbach, G. Time reversal invariance in finance. Quant. Financ. 2009, 9, 505–515. [Google Scholar] [CrossRef]
- Flanagan, R.; Lacasa, L. Irreversibility of financial time series: A graph-theoretical approach. Phys. Lett. A 2016, 380, 1689–1697. [Google Scholar] [CrossRef]
- Zanin, M.; Rodríguez-González, A.; Menasalvas Ruiz, E.; Papo, D. Assessing time series reversibility through permutation patterns. Entropy 2018, 20, 665. [Google Scholar]
- Fama, E.F. Efficient capital markets a review of theory and empirical work. Fama Portf. 2021, 76–121. [Google Scholar] [CrossRef]
- Eom, C.; Oh, G.; Jung, W.S. Relationship between efficiency and predictability in stock price change. Phys A Stat. Mech. Its Appl. 2008, 387, 5511–5517. [Google Scholar] [CrossRef]
- Fong, W.M. Time reversibility tests of volume–volatility dynamics for stock returns. Econ. Lett. 2003, 81, 39–45. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Gu, R.; Cao, J.; Wang, H. Analysis of market efficiency for the Shanghai stock market over time. Phys. A Stat. Mech. Its Appl. 2010, 389, 1635–1642. [Google Scholar] [CrossRef]
- Jiang, C.; Shang, P.; Shi, W. Multiscale multifractal time irreversibility analysis of stock markets. Phys A. Stat. Mech. Its Appl. 2016, 462, 492–507. [Google Scholar] [CrossRef]
- González-Espinoza, A.; Martínez-Mekler, G.; Lacasa, L. Arrow of time across five centuries of classical music. Phys. Rev. Res. 2020, 2, 033166. [Google Scholar] [CrossRef]
- Lucia, U. The gouy-stodola theorem in bioenergetic analysis of living systems (Irreversibility in bioenergetics of living systems). Energies 2014, 7, 5717–5739. [Google Scholar] [CrossRef]
- Zotin, A.; Zotin, A.I. Phenomenological theory of ontogenesis. Int. J. Dev. Biol. 2004, 41, 917–921. [Google Scholar]
- Roldán, É.; Barral, J.; Martin, P.; Parrondo, J.M.; Jülicher, F. Quantifying entropy production in active fluctuations of the hair-cell bundle from time irreversibility and uncertainty relations. New J. Phys. 2021, 23, 083013. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Broken asymmetry of the human heartbeat: Loss of time irreversibility in aging and disease. Phys. Rev. Lett. 2005, 95, 198102. [Google Scholar] [CrossRef] [PubMed]
- Guzik, P.; Piskorski, J.; Krauze, T.; Wykretowicz, A.; Wysocki, H. Heart rate asymmetry by Poincaré plots of RR intervals. Biomed. Technol. 2006, 51, 272–275. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Guzzetti, S.; Montano, N.; Gnecchi-Ruscone, T.; Furlan, R.; Malliani, A. Time Reversibility in Short-Term Heart Period Variability; IEEE: Piscataway, NJ, USA, 2006; pp. 77–80. [Google Scholar]
- Porta, A.; Casali, K.R.; Casali, A.G.; Gnecchi-Ruscone, T.; Tobaldini, E.; Montano, N.; Lange, S.; Geue, D.; Cysarz, D.; Van Leeuwen, P. Temporal asymmetries of short-term heart period variability are linked to autonomic regulation. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 295, R550–R557. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; D’addio, G.; Bassani, T.; Maestri, R.; Pinna, G.D. Assessment of cardiovascular regulation through irreversibility analysis of heart period variability: A 24 hours Holter study in healthy and chronic heart failure populations. Philos. Trans. R. Soc. A 2009, 367, 1359–1375. [Google Scholar] [CrossRef] [PubMed]
- Piskorski, J.; Guzik, P. Geometry of the Poincaré plot of RR intervals and its asymmetry in healthy adults. Physiol. Meas. 2007, 28, 287. [Google Scholar] [CrossRef]
- Karmakar, C.K.; Khandoker, A.; Gubbi, J.; Palaniswami, M. Defining asymmetry in heart rate variability signals using a Poincaré plot. Physiol. Meas. 2009, 30, 1227. [Google Scholar] [CrossRef]
- Hou, F.; Zhuang, J.; Bian, C.; Tong, T.; Chen, Y.; Yin, J.; Qiu, X.; Ning, X. Analysis of heartbeat asymmetry based on multi-scale time irreversibility test. Phys. A Stat. Mech. Its Appl. 2010, 389, 754–760. [Google Scholar] [CrossRef]
- Hunt, B.E.; Farquhar, W.B. Nonlinearities and asymmetries of the human cardiovagal baroreflex. Am. J. Physiol. 2005, 288, R1339–R1346. [Google Scholar] [CrossRef]
- Timmer, J.; Gantert, C.; Deuschl, G.; Honerkamp, J. Characteristics of hand tremor time series. Biol. Cybern. 1993, 70, 75–80. [Google Scholar] [CrossRef]
- Orellana, J.N.; Sixto, A.S.; Torres, B.D.L.C.; Cachadina, E.S.; Martín, P.F.; de la Rosa, F.B. Multiscale time irreversibility: Is it useful in the analysis of human gait? Biomed. Signal Process. Control 2018, 39, 431–434. [Google Scholar] [CrossRef]
- Martín-Gonzalo, J.A.; Pulido-Valdeolivas, I.; Wang, Y.; Wang, T.; Chiclana-Actis, G.; Algarra-Lucas, M.d.C.; Palmí-Cortés, I.; Fernandez Travieso, J.; Torrecillas-Narváez, M.D.; Miralles-Martinez, A.A.; et al. Permutation entropy and irreversibility in gait kinematic time series from patients with mild cognitive decline and early Alzheimer’s dementia. Entropy 2019, 21, 868. [Google Scholar] [CrossRef]
- Paluš, M. Nonlinearity in normal human EEG: Cycles, temporal asymmetry, nonstationarity and randomness, not chaos. Biol. Cybern. 1996, 75, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Van der Heyden, M.; Diks, C.; Pijn, J.; Velis, D. Time reversibility of intracranial human EEG recordings in mesial temporal lobe epilepsy. Phys. Lett. A 1996, 216, 283–288. [Google Scholar] [CrossRef]
- Ehlers, C.L.; Havstad, J.; Prichard, D.; Theiler, J. Low doses of ethanol reduce evidence for nonlinear structure in brain activity. J. Neurosci. 1998, 18, 7474–7486. [Google Scholar] [CrossRef]
- Visnovcova, Z.; Mestanik, M.; Javorka, M.; Mokra, D.; Gala, M.; Jurko, A.; Calkovska, A.; Tonhajzerova, I. Complexity and time asymmetry of heart rate variability are altered in acute mental stress. Physiol. Meas. 2014, 35, 1319. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Güntekin, B.; Aktürk, T.; Hanoğlu, L.; Papo, D. Time irreversibility of resting-state activity in the healthy brain and pathology. Front. Physiol. 2020, 10, 1619. [Google Scholar] [CrossRef]
- Yao, W.; Dai, J.; Perc, M.; Wang, J.; Yao, D.; Guo, D. Permutation-based time irreversibility in epileptic electroencephalograms. Nonlinear Dyn. 2020, 100, 907–919. [Google Scholar] [CrossRef]
- Xiong, H.; Shang, P.; Hou, F.; Ma, Y. Visibility graph analysis of temporal irreversibility in sleep electroencephalograms. Nonlinear Dyn. 2019, 96, 1–11. [Google Scholar] [CrossRef]
- De la Fuente, L.A.; Zamberlan, F.; Bocaccio, H.; Kringelbach, M.L.; Deco, G.; Perl, Y.S.; Tagliazucchi, E. Temporal irreversibility of neural dynamics as a signature of consciousness. bioRxiv 2021. [Google Scholar] [CrossRef]
- Deco, G.; Perl, Y.S.; Sitt, J.D.; Tagliazucchi, E.; Kringelbach, M.L. Deep learning the arrow of time in brain activity: Characterising brain-environment behavioural interactions in health and disease. bioRxiv 2021. [Google Scholar] [CrossRef]
- Schindler, K.; Rummel, C.; Andrzejak, R.G.; Goodfellow, M.; Zubler, F.; Abela, E.; Wiest, R.; Pollo, C.; Steimer, A.; Gast, H. Ictal time-irreversible intracranial EEG signals as markers of the epileptogenic zone. Clin. Neurophysiol. 2016, 127, 3051–3058. [Google Scholar] [CrossRef]
- Martínez, J.H.; Herrera-Diestra, J.L.; Chavez, M. Detection of time reversibility in time series by ordinal patterns analysis. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 123111. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Lacasa, L.; Flanagan, R. Time reversibility from visibility graphs of nonstationary processes. Phys. Rev. E 2015, 92, 022817. [Google Scholar] [CrossRef] [PubMed]
- Broock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Brock, W.A.; Hsieh, D.A.; LeBaron, B.D.; Brock, W.E. Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Rothman, P. The comparative power of the TR test against simple threshold models. J. Appl. Econom. 1992, 7, S187–S195. [Google Scholar] [CrossRef]
- Daw, C.; Finney, C.; Kennel, M. Symbolic approach for measuring temporal “irreversibility”. Phys. Rev. E 2000, 62, 1912. [Google Scholar] [CrossRef]
- Graff, G.; Graff, B.; Kaczkowska, A.; Makowiec, D.; Amigó, J.; Piskorski, J.; Narkiewicz, K.; Guzik, P. Ordinal pattern statistics for the assessment of heart rate variability. Eur. Phys. J. Spec. Top. 2013, 222, 525–534. [Google Scholar] [CrossRef]
- Li, J.; Shang, P.; Zhang, X. Time series irreversibility analysis using Jensen–Shannon divergence calculated by permutation pattern. Nonlinear Dyn. 2019, 96, 2637–2652. [Google Scholar] [CrossRef]
- Yao, W.; Yao, W.; Wang, J.; Dai, J. Quantifying time irreversibility using probabilistic differences between symmetric permutations. Phys. Lett. A 2019, 383, 738–743. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Zanin, M.; Olivares, F. Ordinal patterns-based methodologies for distinguishing chaos from noise in discrete time series. Commun. Phys. 2021, 4, 1–14. [Google Scholar] [CrossRef]
- Grosse, I.; Bernaola-Galván, P.; Carpena, P.; Román-Roldán, R.; Oliver, J.; Stanley, H.E. Analysis of symbolic sequences using the Jensen-Shannon divergence. Phys. Rev. E 2002, 65, 041905. [Google Scholar] [CrossRef] [PubMed]
- Cammarota, C.; Rogora, E. Time reversal, symbolic series and irreversibility of human heartbeat. Chaos Solitons Fractals 2007, 32, 1649–1654. [Google Scholar] [CrossRef]
- Zanin, M. Assessing time series irreversibility through micro-scale trends. Chaos: Interdiscip. J. Nonlinear Sci. 2021, 31, 103118. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Luque, B.; Lacasa, L.; Ballesteros, F.; Luque, J. Horizontal visibility graphs: Exact results for random time series. Phys. Rev. E 2009, 80, 046103. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Costa, L.d.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Lacasa, L.; Nunez, A.; Roldán, É.; Parrondo, J.M.; Luque, B. Time series irreversibility: A visibility graph approach. Eur. Phys. J. B 2012, 85, 1–11. [Google Scholar] [CrossRef]
- Epps, T.; Singleton, K.J. An omnibus test for the two-sample problem using the empirical characteristic function. J. Stat. Comput. Simul. 1986, 26, 177–203. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Donges, J.F.; Donner, R.V.; Kurths, J. Testing time series irreversibility using complex network methods. Europhys. Lett. 2013, 102, 10004. [Google Scholar] [CrossRef]
- Diks, C.; Van Zwet, W.; Takens, F.; DeGoede, J. Detecting differences between delay vector distributions. Phys. Rev. E 1996, 53, 2169. [Google Scholar] [CrossRef]
- Wang, X.; Shang, P.; Fang, J. Traffic time series analysis by using multiscale time irreversibility and entropy. Chaos: Interdiscip. J. Nonlinear Sci. 2014, 24, 032102. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Ramirez, J.; Rodriguez, E.; Echeverria, J.C. A DFA approach for assessing asymmetric correlations. Phys. A Stat. Mech. Its Appl. 2009, 388, 2263–2270. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Yang, P.; Shang, P. Relative asynchronous index: A new measure for time series irreversibility. Nonlinear Dyn. 2018, 93, 1545–1557. [Google Scholar] [CrossRef]
- Wu, Z.; Shang, P.; Xiong, H. An improvement of the measurement of time series irreversibility with visibility graph approach. Phys. A Stat. Mech. Its Appl. 2018, 502, 370–378. [Google Scholar] [CrossRef]
- Li, J.; Shang, P. Time irreversibility of financial time series based on higher moments and multiscale Kullback–Leibler divergence. Phys. A Stat. Mech. Its Appl. 2018, 502, 248–255. [Google Scholar] [CrossRef]
- Rong, L.; Shang, P. New irreversibility measure and complexity analysis based on singular value decomposition. Phys. A Stat. Mech. Its Appl. 2018, 512, 913–924. [Google Scholar] [CrossRef]
- Choudhary, G.I.; Aziz, W.; Fränti, P. Detection of time irreversibility in interbeat interval time series by visible and nonvisible motifs from horizontal visibility graph. Biomed. Signal Process. Control 2020, 62, 102052. [Google Scholar] [CrossRef]
- Shang, B.; Shang, P. Directed vector visibility graph from multivariate time series: A new method to measure time series irreversibility. Nonlinear Dyn. 2021, 104, 1737–1751. [Google Scholar] [CrossRef]
- Salgado-Garcia, R.; Maldonado, C. Estimating entropy rate from censored symbolic time series: A test for time-irreversibility. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 013131. [Google Scholar] [CrossRef] [PubMed]
- Dabelow, L.; Bo, S.; Eichhorn, R. Irreversibility in active matter systems: Fluctuation theorem and mutual information. Phys. Rev. X 2019, 9, 021009. [Google Scholar] [CrossRef]
- Mori, H.; Kuramoto, Y. Dissipative Structures and Chaos; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin, Germany, 2000; pp. 1–15. [Google Scholar]
- Zhang, X.L.; Begleiter, H.; Porjesz, B.; Wang, W.; Litke, A. Event related potentials during object recognition tasks. Brain Res. Bull. 1995, 38, 531–538. [Google Scholar] [CrossRef]
- Cao, R.; Wu, Z.; Li, H.; Xiang, J.; Chen, J. Disturbed connectivity of EEG functional networks in alcoholism: A graph-theoretic analysis. Bio-Med Mater. Eng. 2014, 24, 2927–2936. [Google Scholar] [CrossRef]
- Zanin, M.; Belkoura, S.; Gomez, J.; Alfaro, C.; Cano, J. Uncertainty in Functional Network Representations of Brain Activity of Alcoholic Patients. Brain Topogr. 2021, 34, 6–18. [Google Scholar] [CrossRef]
- Snodgrass, J.G.; Vanderwart, M. A standardized set of 260 pictures: Norms for name agreement, image agreement, familiarity, and visual complexity. J. Exp. Psychol. Hum. Learn. Mem. 1980, 6, 174. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bressert, E. SciPy and NumPy: An Overview for Developers; O’Reilly Media, Inc.: Newton, MA, USA, 2012. [Google Scholar]
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A llvm-based python jit compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Austin, TX, USA, 15 November 2015; pp. 1–6. [Google Scholar]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Burykin, A.; Costa, M.D.; Peng, C.K.; Goldberger, A.L.; Buchman, T.G. Generating signals with multiscale time irreversibility: The asymmetric weierstrass function. Complexity 2011, 16, 29–38. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lan, G.; Sartori, P.; Neumann, S.; Sourjik, V.; Tu, Y. The energy–speed–accuracy trade-off in sensory adaptation. Nat. Phys. 2012, 8, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Still, S.; Sivak, D.A.; Bell, A.J.; Crooks, G.E. Thermodynamics of prediction. Phys. Rev. Lett. 2012, 109, 120604. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Stochastic thermodynamics: Principles and perspectives. Eur. Phys. J. B 2008, 64, 423–431. [Google Scholar] [CrossRef]
- Peliti, L.; Pigolotti, S. Stochastic Thermodynamics: An Introduction; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Esposito, M. Stochastic thermodynamics under coarse graining. Phys. Rev. E 2012, 85, 041125. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. From stochastic thermodynamics to thermodynamic inference. Annu. Rev. Condens. Matter Phys. 2019, 10, 171–192. [Google Scholar] [CrossRef]
- Rupprecht, J.F.; Prost, J. A fresh eye on nonequilibrium systems. Science 2016, 352, 514–515. [Google Scholar] [CrossRef] [PubMed]
- Martínez, I.A.; Bisker, G.; Horowitz, J.M.; Parrondo, J.M. Inferring broken detailed balance in the absence of observable currents. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Egolf, D.A. Equilibrium regained: From nonequilibrium chaos to statistical mechanics. Science 2000, 287, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Adv. Phys. 2015, 64, 1–137. [Google Scholar] [CrossRef]
- Fang, X.; Kruse, K.; Lu, T.; Wang, J. Nonequilibrium physics in biology. Rev. Mod. Phys. 2019, 91, 045004. [Google Scholar] [CrossRef]
- Skinner, D.J.; Dunkel, J. Improved bounds on entropy production in living systems. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef] [PubMed]
- Skinner, D.J.; Dunkel, J. Estimating entropy production from waiting time distributions. arXiv 2021, arXiv:2105.08681. [Google Scholar]
- Seara, D.S.; Machta, B.B.; Murrell, M.P. Irreversibility in dynamical phases and transitions. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]









| Test | Parameter | Values |
|---|---|---|
| BDS | none | |
| Ramsey | k | |
| DFK | n | |
| L | ||
| Permutation patterns | 3 | |
| Ternary Coding | Number of segments | 20 |
| 10th percentile of | ||
| MSTrends | ||
| d | 1 | |
| Visibility graph | none | |
| LocalCC | none |
| Module (test) | Reference | Parameter | Meaning |
|---|---|---|---|
| BDS | [87,88] | none | |
| Ramsey | [49] | kappa | The lag k |
| DFK | [90] | n | Number of possible symbols |
| L | Word length | ||
| PermPatterns | [52,84,92,93] | none | |
| TernaryCoding | [98] | segL | Length of the segments on which is calculated |
| alpha | Threshold for symbolisation | ||
| MSTrends | [99] | wSize | Length of overlapping windows |
| wSize2 | Length of windows used to calculate higher central moments | ||
| VisibilityGraph | [99] | none | |
| LocalCC | [107] | none | |
| Pomeau | [5] | numRnd | Number of random repetitions to extract the p-value |
| tau | Embedding delay | ||
| Diks | [108] | embD | Embedding dimension, or size of each vector |
| dVar | Bandwidth of the analysis | ||
| Ens_BDS_MSTrends | none |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanin, M.; Papo, D. Algorithmic Approaches for Assessing Irreversibility in Time Series: Review and Comparison. Entropy 2021, 23, 1474. https://doi.org/10.3390/e23111474
Zanin M, Papo D. Algorithmic Approaches for Assessing Irreversibility in Time Series: Review and Comparison. Entropy. 2021; 23(11):1474. https://doi.org/10.3390/e23111474
Chicago/Turabian StyleZanin, Massimiliano, and David Papo. 2021. "Algorithmic Approaches for Assessing Irreversibility in Time Series: Review and Comparison" Entropy 23, no. 11: 1474. https://doi.org/10.3390/e23111474
APA StyleZanin, M., & Papo, D. (2021). Algorithmic Approaches for Assessing Irreversibility in Time Series: Review and Comparison. Entropy, 23(11), 1474. https://doi.org/10.3390/e23111474







