Invariance Properties of the Entropy Production, and the Entropic Pairing of Inertial Frames of Reference by Shear-Flow Systems
Abstract
:1. Introduction
- (1)
- First law (law of inertia): Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.
- (2)
- Second law (equation of motion): The alteration of motion is ever proportional to the motive force impressed, and is made in the direction of the right line in which that force is impressed.
- (3)
- Third law (law of action and reaction): To every action there is always opposed an equal reaction, or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.
2. Thermodynamic Entropy Balance and Entropy Production
3. Invariance Properties
- (I)
- Dimensionless invariance: As established by nearly two centuries of mathematical and physical insight [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], a fundamental property of a conservation equation is its invariance to dimensionless transformations. Carvallo [10] and Vaschy [12] referred to this as similitude, later also described as similarity or self-similarity, e.g., [5,15,46,47,48,49,50,51,52,53] (n.b., some researchers use similarity as the general term, reserving self-similarity for systems with a solution similar to itself, such as a fractal [21]). Birkhoff [20] interpreted similarity from the perspective of group theory, as invariance under the “dimensional group of positive scalar transformations of units”. Some researchers, e.g., [18,22,23] distinguish between complete similarity or self similarity of the first kind, which can be revealed by dimensional analysis alone, and incomplete similarity or self similarity of the second kind, which cannot be revealed purely by dimensional analysis, due to divergent asymptotic behaviour of the governing equations in the limit of one or more dimensionless groups. The second category has been analyzed by the method of intermediate asymptotics [21,22,23], shown to be closely related to the method of renormalization groups, e.g., [22,23,25,54].To transform the local entropy production, we choose an appropriate length scale L, velocity scale , temperature scale , and density scale , to define the following dimensionless variables:where , and R are, respectively, the dimensionless time, position, velocity, and density. Using the scaling parameters, we also construct the following dimensionless groups:The geometric scaling conditions impose the condition of geometric similarity; the velocities and fluxes impose the condition of kinematic similarity; while the remaining groups impose the equivalence of forces, or dynamic similarity [47,48,49,50,51,52].Substitution of (11)–(14) into (6) and simplification gives the nondimensional entropy production equation:This system consists of 17 dimensional parameters , counting each vector component and the four introduced scaling parameters, with 4 classical dimensions {s, m, kg, K} (here written in SI units rather than the usual dimensional notation). Applying the Buckingham theorem [15], we confirm that this yields a nondimensional equation between dimensionless groups .For anisotropic systems, (15) can be rewritten in the more comprehensive formulation:which incorporates the vector dimensionless group:where ⊙ is the element-wise (Hadamard) product of two vectors to give a vector, and ⊘ is an element-wise division operator between two vectors. As evident, expresses the component-wise ratios of the nonfluid and fluid entropy fluxes. Other dimensionless forms of (6) can also be derived using different choices of the reference parameters, e.g., [40,41,42].In either form (15) or (16), the nondimensional entropy production equation is invariant to transformations that maintain the same values of the dimensionless groups (11)–(14) (or with (17)), known as dimensionless invariance. Provided that the assumptions inherent in the derivation of (6) do not break down, such systems satisfy the properties of geometric, kinematic, and dynamic similarity, and will exhibit the same physics regardless of their absolute scale.
- (II)
- Invariance to fixed displacements in the time or position coordinates: For this, we adopt the modified dimensionless coordinates [5,20]:based on constant displacements and , respectively, in the time and position coordinates, with the velocities, density, and other dimensionless variables unchanged. This transformation of (6) returns (15), hence (15) is invariant to fixed displacements of the time or position coordinates.
- (III)
- (IV)
- Time antisymmetry: Here we consider reversal of the time coordinate, and also of the velocities and fluxes, in dimensionless form [5]:with the positions, density, and other dimensionless variables unchanged. Transformation of (6) then yields the negative of (15) on the right-hand side. Equation (15) therefore exhibits antisymmetry with respect to time reversal, as expected for an entropy production equation.
- (V)
- Galilean invariance: For this we adopt the dimensionless velocities and fluxes [5,20]:based on the constant velocity , which provides a Galilean transformation between two inertial frames of reference. The time, density, and other dimensionless variables are unchanged. This transformation of (6) returns (15), hence (15) is Galilean invariant.
- (VI)
- Lie invariance: The invariance properties or symmetries associated with infinitesimal Lie transformations of a differential or integral equation constitutes a large topic, e.g., [25,26,55,56,57,58]. For the present study, we restrict the discussion to the one-parameter Lie group of point scaling transformations, e.g., [25,26,27,28,29,30]. For the local entropy production (6), this is defined by the 13-parameter map:where is a scaling parameter, are the scaling exponents, and the capital or Greek letters denote the transformed variables (here, not necessarily dimensionless). Substitution into (6) and simplification gives the mathematical form (15) subject to 7 auxiliary relations for , which can be solved to give:This result can be interpreted in several ways:
- (a)
- If the transformed parameters in (22) have the same dimensions as the original parameters—the standard interpretation—they must be considered as rescaled dimensional variables, while the terms are dimensionless conversion factors. Transformation gives a rescaled form of (6) rather than a nondimensional equation, while the auxiliary relations (23) provide the relations between conversion factors for the dependent and independent variables. This interpretation is useful, representing a rescaling between a model and a prototype to maintain similarity, e.g., [27,28,29], or rescaling by a change of units. However, since this interpretation can be handled by the more general apparatus of dimensionless invariance (I), it need not be considered further.
- (b)
- Alternatively, if the transformed variables in (22) are intended to be dimensionless, the terms must be interpreted as dimensional scaling parameters. Assuming a positive dimensionless parameter , each term will carry the base- logarithm of the dimensions of quantity i. As an example, the relation carries the dimensions , written in SI units. In consequence, the auxiliary relations (23) simply express the relations between the dependent and independent dimensions within the system, enabling the transformation of (6) into the nondimensional form (15).In this example, there are 7 auxiliary relations (23) composed of 13 terms, so there must be independent terms, hence, 6 independent dimensions of the system. We have chosen to express (6) in terms of the dimensions {s, m, m, m, kg m−1 m−1 m−1, J K−1 kg−1} of the 6 linearly independent parameters , counting each vector component of , to span the set of 6 fundamental units {s, m, m, m, kg, K}. This choice of dimensions—which distinguishes the length scale in each Cartesian direction, and which adopts the dimensions of the fluid density and specific entropy rather than mass and temperature—is rather unexpected, but it does represent the intrinsic or “indigenous” dimensions of the local entropy production (6). Other choices of independent variables are possible, provided that they span the set of 6 fundamental units. The resulting Lie transformation (22) and (23) is consistent with the Buckingham theorem [15], reducing a system of parameters (including the 6 independent terms) and 6 dimensions to the nondimensional form (15) with dimensionless groups. It is curious that the number and character of the dimensions and the vector formulation of (15) are revealed automatically by the Lie apparatus, seemingly for free!
- (c)
- We can also consider hydrid interpretations, in which the transformed parameters and the terms in (22) both carry dimensions, in combination giving those of the original parameters. Such representations may be feasible, but owing to their complexity, we exclude them from further discussion.
We see that the second interpretation (b) of the Lie transformation provides an alternative formulation of the dimensionless invariance (I), expressed in terms of fundamental quantities that better reflect the underlying symmetries of (6). This equivalence between dimensionless invariance and Lie point symmetry has been recognized by some researchers, e.g., [56], but is not well-known in either the mathematical or engineering literature. By remapping the scaling parameters in the manner of (18)–(21), we can also extract the other invariances (II)–(V), hence, the Lie invariance can be considered to subsume all of these invariances.In their analyses of other conservation laws, some authors deduce further equivalences, which for the present study would yield , and , e.g., [27,29]. These relations are not provided by the above Lie transformation of (6), nor are they evident from its vector structure. They can, however, be interpreted as consequences of the invariance to fixed rotations or reflections of the coordinate system (III).We note that Lie and later workers developed comprehensive algorithmic methods for the analysis of infinitesimal Lie symmetries of differential equations [20,26,28,55,57,58]. Furthermore, several researchers have suggested multiparametric extensions of the above Lie apparatus, applicable to all conservation equations [26,58,59,60]. The current level of understanding of the Lie invariances of the local entropy production (6) is therefore incomplete, and warrants further examination.
4. Macroscopic Shear Flow Systems and an Entropic Invariance Principle
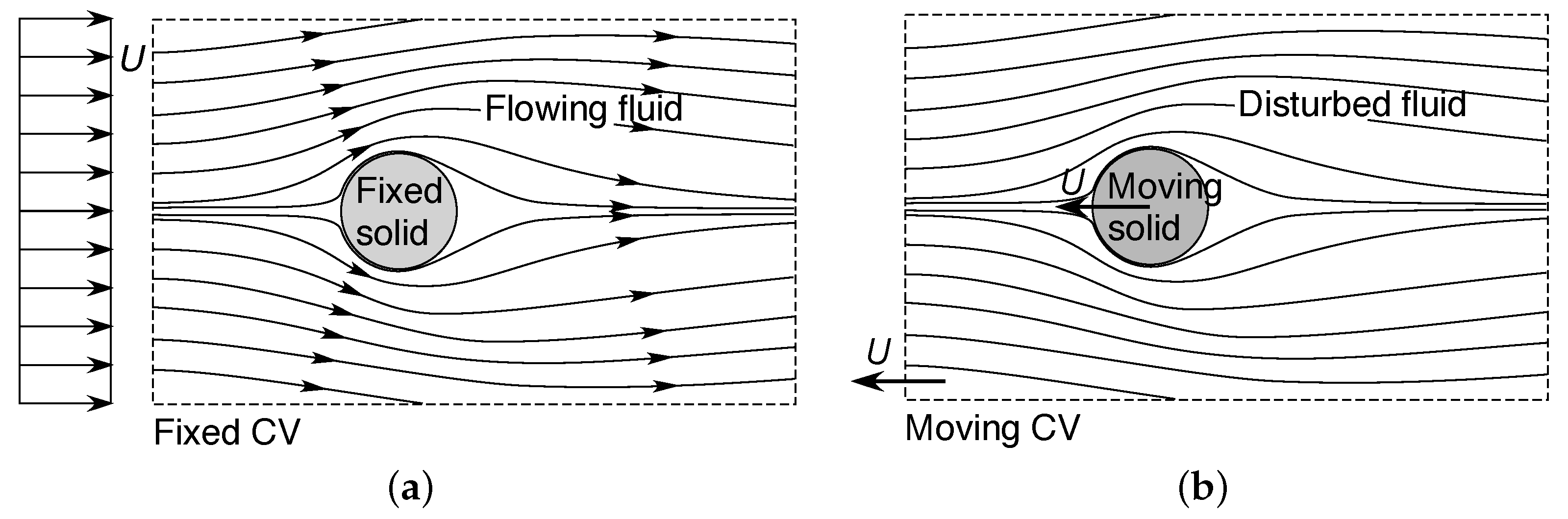
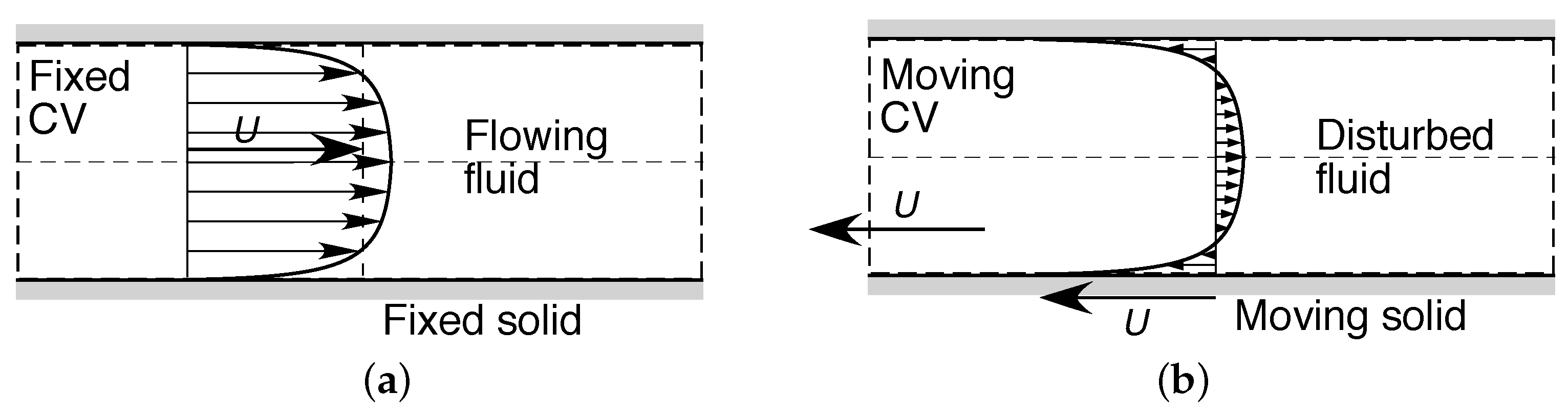
4.1. External and Internal Shear Flow Systems
4.1.1. External Flows
4.1.2. Internal Flows
4.2. An Invariance Principle of Entropic Pairing
- (a)
- Laminar flow, in which the diffusion of momentum is dominated by viscous processes, leading to a low Reynolds number and lower entropy production, and
- (b)
- Turbulent flow, in which the diffusion of momentum is dominated by inertial processes, leading to a higher Reynolds number and a commensurately higher rate of entropy production.
4.3. An Entropic Paradox and Its Resolution
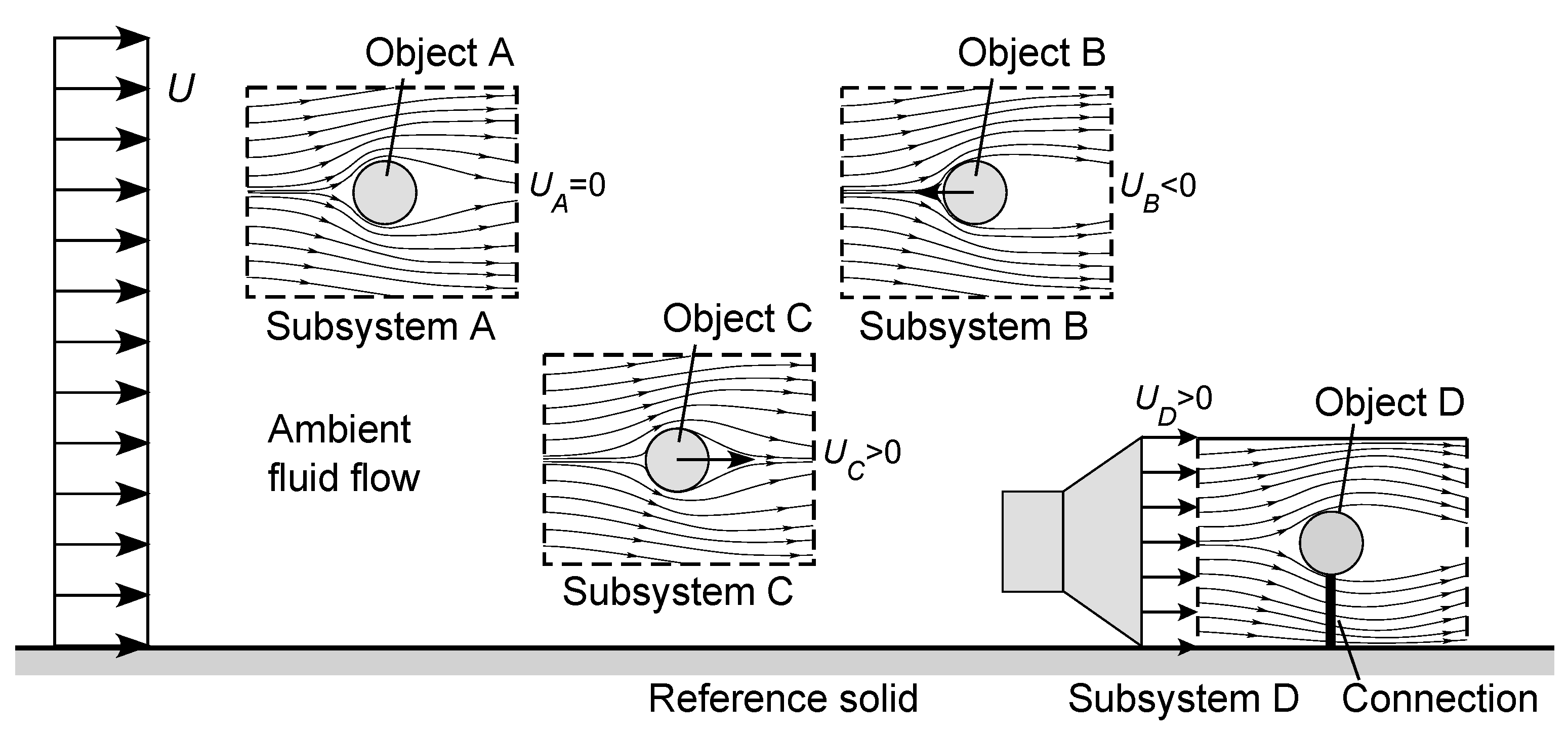
4.3.1. Statement of the Paradox
- (a)
- Subsystem A, containing Object A, which is stationary with respect to the reference solid (), and experiences an incoming flow field of ambient velocity U;
- (b)
- Subsystem B, containing Object B moving at the speed relative to the reference solid (i.e., in motion upstream);
- (c)
- Subsystem C, containing Object C moving at the speed relative to the reference solid (i.e., in motion downstream); and
- (d)
- Subsystem D, consisting of an internal flow field of ambient velocity established within a container or region, within which Object D is held stationary with respect to the Subsystem D boundary and the reference solid.
4.3.2. Resolution of the Paradox
- (a)
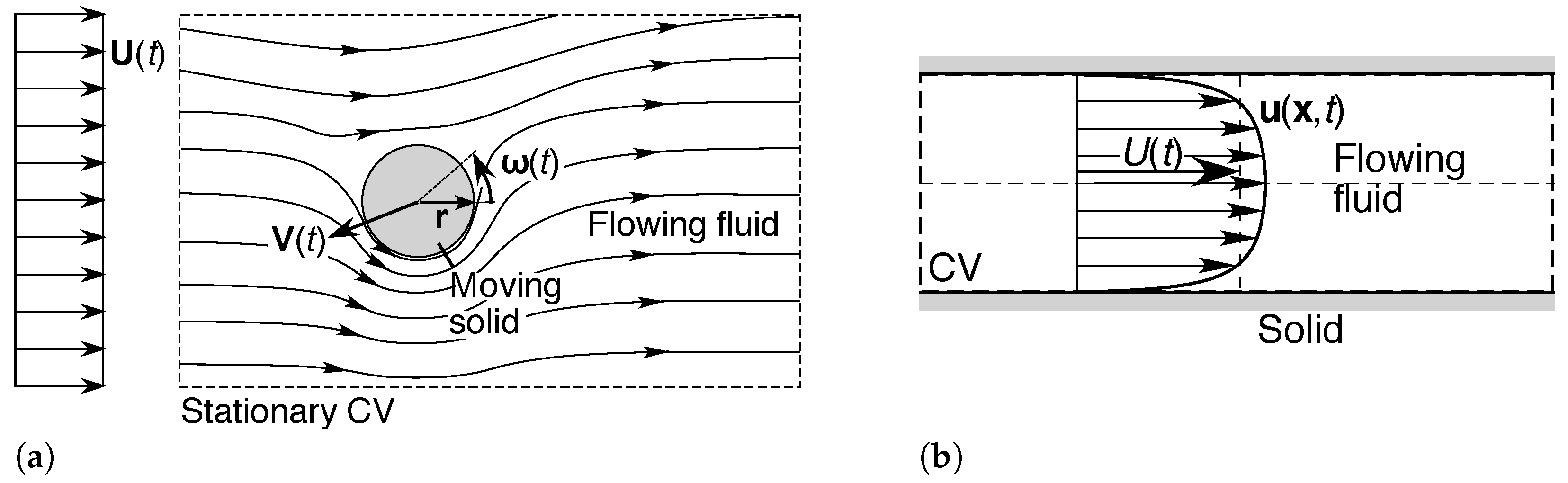
- Subsystem A: From Figure 3, we see that Object A shares the same inertial frame of reference as the reference solid (it could even be joined to it by some physical framework or magnetic coupling). The entropic pair for Subsystem A is, therefore, the same as for the bulk flow, with the inertial separation U. Furthermore, the entropy production (36) reveals the existence of a source of negentropy for Subsystem A, which is being continuously depleted by the reaction to the drag force, i.e., by the need to continuously do work against the frictional and pressure drag between the fluid and Object A. This rate of work is, at minimum, (assuming 100% efficiency), and the associated rate of negentropy consumption is, at minimum, , or in dimensionless form . From the information provided in Figure 3, we do not know if this source of negentropy is situated at Object A itself, for example, a source of motive power attached to the object, or if it is incurred by the source of negentropy driving the ambient fluid stream, enabling it to perform the required added work against Object A held in a fixed position. We do know, however, that there must be a source of negentropy for Subsystem A, and that this must be situated with either (or both) Object A or the ambient flow field.
- (b)
- Subsystem B: Now consider Subsystem B, which preferences the entropic pair of inertial frames of reference defined by the ambient flow and Object B, with the inertial separation . In all cases for which (moving upstream), this entropic pair will differ from that for the ambient flow, due to the different solid velocities. There must be a source of negentropy for the entropy production incurred by Subsystem B. Furthermore—and this is the crucial point—even if there is a physical connection or coupling between Object B and the reference solid (e.g., a chassis and a set of wheels), we know that the ambient flow field can only contribute to this entropy production to the extent of its inertial separation U from the reference solid, i.e., for which:(assuming a constant length scale and cross-sectional area). Any positive excess must therefore be incurred by an independent source of negentropy associated with Object B, for example a source of motive power attached to this object, or connected to it by other means such as a magnetic coupling. Alternatively, if there is no connection between Object B and the reference solid, nor with any other solid in the system, then all of the negentropy consumption for Subsystem B, not just the excess , must be incurred by the source attached to Object B.
- (c)
- Subsystem C: Next, consider Subsystem C, which preferences the entropic pair of inertial frames defined by the ambient stream and Object C, with the inertial separation . The Reynolds number, drag coefficient, and entropy production are given in (35) and (36). For the downstream motion () of Object C, there are three scenarios:
- (i)
- For , Object C will move more slowly than the downstream flow, and the subsystem will have a positive , , and entropy production.
- (ii)
- For the special case , Object C will move with the fluid stream, hence, , , so (for this ideal case) there is no entropic pair of inertial frames of reference and no entropy production.
- (iii)
- For , Object C will move more rapidly than the downstream flow, incurring a drag force in the opposite direction, again leading to a positive , , and entropy production.
As for Subsystem B, the ambient flow can only contribute to the entropy production of Subsystem C to the extent of its inertial separation U, i.e., for which:The excess will be negative (non-physical), zero, or positive, respectively, for the above three cases. For case (i), it is thus possible for all of the negentropy consumption to be harnessed from the ambient flow, with the solid object partly carried by the fluid. For case (ii), both terms in the excess vanish, and there is no entropy production. For case (iii), however, the positive excess reveals the existence of a source of negentropy for Object C, independent of that for the ambient flow. Alternatively, regardless of the above categories, if the negentropy harnessed by Object C from the flow is less than , then this difference must also be provided by the independent source of negentropy for Object C.If the object is in translational motion in a different direction to the surrounding flow field, the above arguments must be modified to account for the relative velocity vectors. For example, consider an ambient flow of velocity U, within which Object C moves at the constant velocity U, in both cases measured in Cartesian coordinates with respect to the reference solid. The macroscopic entropy production (10) is now given by the two- or three-dimensional vector scalar product:where is the drag-lift force vector, containing drag and lift components aligned with and normal to the direction of motion, respectively (in three-dimensional systems there can be two lift components). Equation (42) represents the combined effect of frictional and pressure forces. The parameters in (42) can be expressed in terms of a vector Reynolds number and vector drag-lift coefficient, to give:where is the magnitude of vector . As evident from (42) and (43), there must be an acute angle between vectors and (or between and ), to ensure the nonnegativity of the entropy production. From the Kutta-Joukowski theorem, in a potential flow the lift component of will be proportional to the fluid circulation on any closed path around the object, where is the intrinsic coordinate [47,48,52,53,62]. Since a two-dimensional asymmetric object (e.g., an airfoil or hydrofoil) creates a non-zero fluid circulation, it will produce lift. For an object with no lift forces, and will be oriented in the same direction, and we recover in (36) based on scalar variables.Using a mechanism mounted on Object C (e.g., a sail), the ambient flow can be harnessed to extract the negentropy required for motion in almost any direction, but only to some maximum extent that is harnessable from the flow (allowing for the possibility of direction-dependent parameters such as areas, length scales, and drag coefficients). Beyond this, any positive excess must have an independent source of negentropy, most likely attached to the object. Similar arguments apply to other external flow subsystems. Reexamining Object B, we note it may be very difficult to harness the ambient flow to enable countercurrent motion, but it is certainly possible to facilitate motion on an oblique reverse trajectory and to thereby construct a zigzag course (“tacking“) to achieve a net upstream motion. In all cases, the negentropy not actually harnessed from the ambient flow or extracted by a connection to another solid must be provided by the independent source of negentropy associated with the object. - (d)
- Subsystem D: Now consider Subsystem D, an external flow subsystem within an internal flow subsystem, in turn situated within the main flow field. This preferences the entropic pair of inertial frames defined by its internal flow and Object D, with the inertial separation . For the example shown in Figure 3, the surrounding ambient flow field does not directly affect the fluid inertial frame of reference, but due to the connection between Object D and the reference solid, the subsystem has the same solid inertial frame of reference as the ambient flow. For any nonzero , the subsystem will have a positive , and entropy production due to the drag force on Object D, and also a positive , , and entropy production due to the internal flow within Subsystem D. In dimensional form, from (32) the total is:Due to the physical connection between Object D and the reference solid, we know that the source of negentropy for (44) cannot reside with Object D. It is possible that negentropy could be harnessed from the bulk flow, but only to the maximum extent that is harnessable, for example from (10):where is the maximum power extractable by Subsystem and is its reference temperature. For example, considering only the kinetic energy component of the ambient flow, for Subsystem D with the intake area , by continuity , so from (30), . In general, the form of (45) will depend on the design of Subsystem D and its conversion efficiency, so this is not analyzed further here. Here, it is sufficient to state that the excess between (45) and (44), if positive, must be provided by an independent source of negentropy, which in this example must power the mechanism (such as a pump, blower, or compressor) used to create the flow field for Subsystem D. If no negentropy is harnessed from the bulk flow, then all of the total must be provided by this independent source of negentropy.
- (e)
- Other Variants: If we now release Object D from its solid connection, we create an independent external flow subsystem within the internal flow of Subsystem D. At steady state, Object D could harness negentropy from the Subsystem D flow field to provide for its entropy production but only to the extent that this is harnessable. Any excess must be incurred by yet another independent source of negentropy attached to Object D, to maintain it in a fixed position.Finally, we can imagine Subsystem D to be in steady motion with respect to the bulk flow field, thus involving several nested external and internal flow systems. This will require sources of negentropy for the entropy production of all component subsystems. By connections or coupling, some of these could extract negentropy from their surrounding systems, but only to the extent possible, with any excess requiring one or more independent sources of negentropy.
4.3.3. Governing Principles
- (1)(A)
- A shear flow subsystem at steady state, defined by fluid flow relative to a solid object, preferentially selects an entropic pair of inertial frames of reference, consisting of (i) the frame moving with the solid, i.e., that in which the solid is stationary, and (ii) the frame moving with the mean fluid flow, i.e., that in which the mean fluid flow is stationary. These frames are unique. They can be described as being entropically paired by the subsystem and inertially separated by their difference in velocities.
- (2)(A)
- An entropically paired shear flow subsystem must have at least one source of negentropy for its entropy production.
- (3)
- If the entropic pair of a shear flow subsystem differs from the frames of reference that define the surrounding flow, then:
- (A)
- The shear flow subsystem may be harnessing negentropy from its external environment, either from the ambient flow field or by exploiting some other connection, but it can only do so to the extent that these are harnessable by the subsystem.
- (B)
- Any excess entropy production, above what is actually harnessed from the external environment, reveals the existence of at least one independent source of negentropy for the shear flow subsystem.
4.4. Other Steady-State Shear Flow Systems
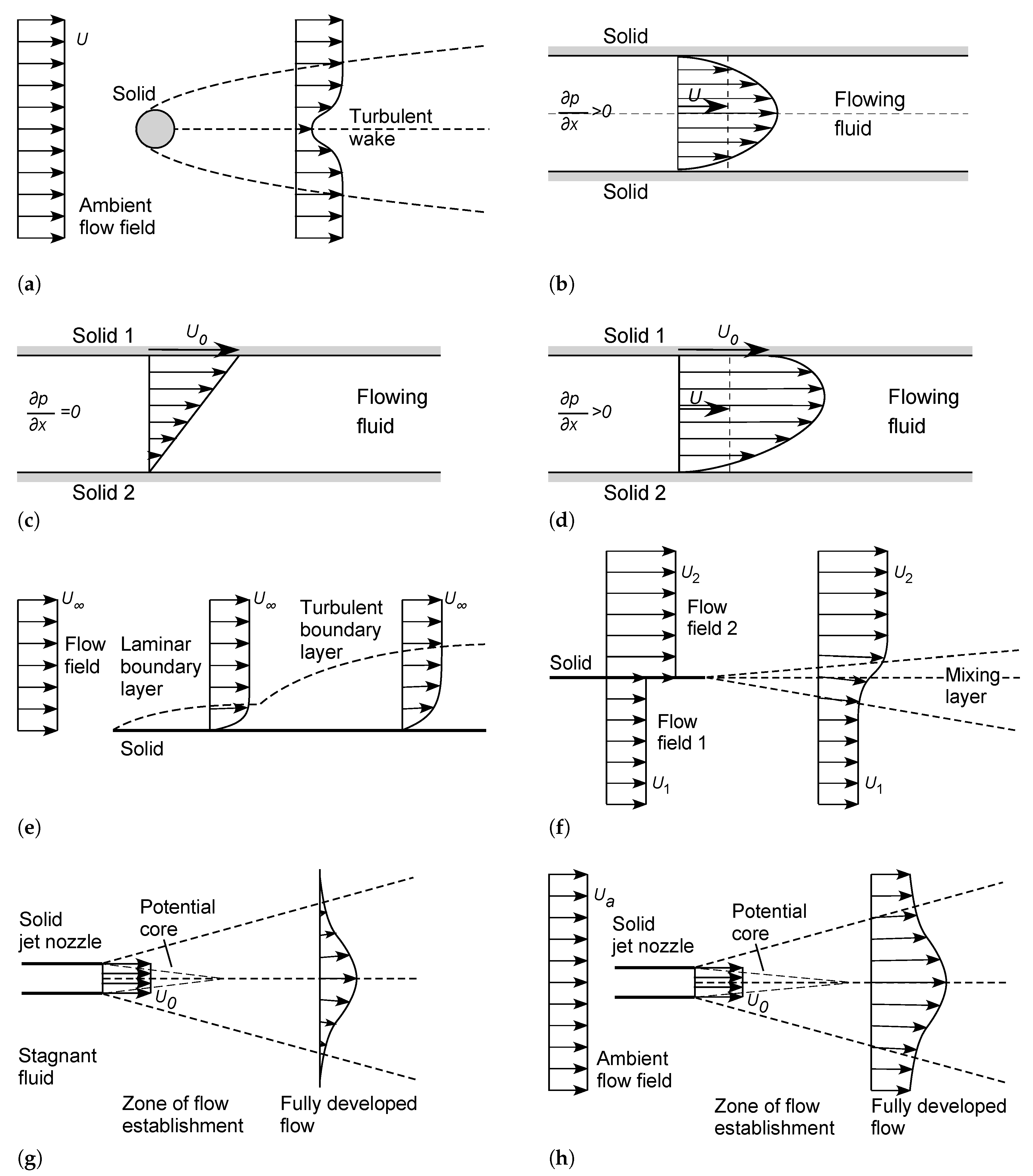
- (a)
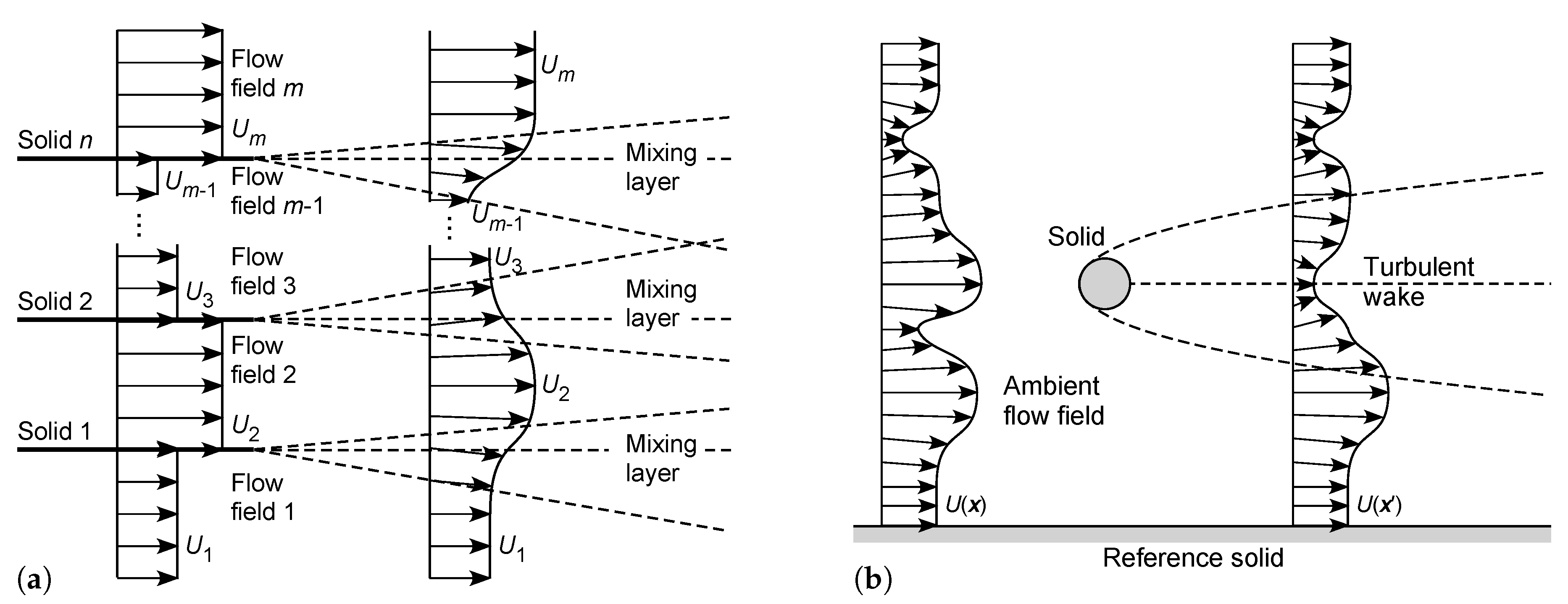
- In a two-dimensional or three-dimensional external flow, as shown in Figure 1 or Figure 4a, the entropic pair consists of the solid and the ambient flow, the latter referenced to its upstream mean velocity profile. In the turbulent wake downstream of the solid, the flow field is subject to nonlocal influences of both the original fluid stream and the solid. As discussed in Section 4.1.1, there must be at least one source of negentropy associated with the solid and/or the ambient flow, to maintain the steady-state flow.
- (b)
- In a two-dimensional or three-dimensional internal flow under a pressure gradient (Poiseuille flow), as shown in Figure 2 or Figure 4b, the entropic pair consists of the solid wall(s) and the internal flow, the latter referenced at its mean velocity. As discussed in Section 4.1.2, there must be at least one source of negentropy, associated with the solid wall(s) and/or the fluid flow, to maintain the steady-state flow.
- (c)
- In Couette flow, involving the relative motion of parallel plates or concentric cylinders in contact with a fluid as shown in Figure 4c, the entropic pair is provided by the two solid walls of the system. At least one of the solids must have an independent source of negentropy, such as an engine connected to a driveshaft or crankshaft, to drive the relative motion, which in turn generates the fluid flow.
- (d)
- In a combined Couette-Poiseuille flow, consisting of fluid flow under a pressure gradient between moving parallel plates or concentric cylinders, as shown in Figure 4d, the two solids and the internal flow (referenced at its mean velocity) provide an entropic triple of inertial frames of reference for the system. From the above principles, there must be at least two independent sources of negentropy: one for the internal flow, and at least one for the relative motions of the solids.
- (e)
- For a boundary layer flow, consisting of fluid flow relative to a solid boundary such as that as shown in Figure 4e, the flow is commonly analyzed using the Reynolds number or , based on the distance x [m] or boundary-layer thickness [m] from the start of the plate, respectively [5,46,47,48,49,50,51,52]. These Reynolds numbers are functions of position, but all contain the same reference velocity . The entropic pair is therefore provided by the solid and the ambient flow (referenced to the upstream flow field or at infinite vertical distance). The system must have at least one source of negentropy, which could be associated with the solid object and/or the ambient flow field.
- (f)
- Consider the two-dimensional turbulent mixing layer, in which two fluid streams separated by a solid plate are allowed to merge beyond the end of the plate, as shown in Figure 4f. Here, the two fluid streams (referenced at infinite distance) and solid provide an entropic triple for the system. This example illustrates the nonlocal influence of a solid on the downstream fluid—its influence cannot be neglected even for long distances downstream. There must be at least two independent sources of negentropy associated with this triple, to drive the two independent flows.
- (g)
- Consider the two-dimensional or axisymmetric turbulent jet issuing into a stationary fluid, as shown in Figure 4g. Here, the solid nozzle and its internal flow field (referenced at its mean velocity) provide the entropic pair for the system. This system again illustrates the nonlocal influence of a solid to create the wedge-shaped or conical zone of fluid flow produced by shear against the ambient fluid. The fluid flow must be driven by at least one independent source of negentropy, associated with the fluid jet and/or solid nozzle.
- (h)
- Consider the two-dimensional or axisymmetric turbulent jet issuing into an ambient parallel flow, as shown in Figure 4h. Here the solid nozzle and two fluid flows provide an entropic triple for the system. There must be at least two independent sources of negentropy associated with this triple, to drive the two fluid flows.
- (1)(B)
- A shear flow subsystem at steady state, generated by the relative motion of two solid objects within a fluid, preferentially selects an entropic pair of inertial frames of reference, consisting of the frames moving with each solid.
- (C)
- A shear flow subsystem at steady state, defined by the relative motions of two solid objects and a fluid stream, or two fluid streams and a solid object, preferentially selects an entropic triple of inertial frames of reference, consisting of the frames moving with each solid and fluid flow. The entropic triple can be analyzed in terms of its three constituent entropic pairs.
- (2)(B)
- An entropically tripled shear flow subsystem must have at least two independent sources of negentropy for its entropy production.
- (1)(D)
- A shear flow subsystem at steady state, defined by the relative motions of m independent solid objects and n independent fluid streams, preferentially selects an entropic -tuple of inertial frames of reference, consisting of the frames moving with each solid and fluid flow. The entropic -tuple can be analyzed in terms of its constituent entropic pairs.
- (2)(C)
- An entropically -tupled shear flow subsystem must have at least independent sources of negentropy for its entropy production.
5. Unsteady Shear Flow Systems
5.1. Unsteady External Flows
- (1)(E)
- A shear flow subsystem in unsteady flow, defined by the relative motions of a fluid and a solid, preferentially selects an entropic pair of frames of reference—or a set of entropic pairs—that is changing in time. At least one frame from each entropic pair will be a non-inertial frame of reference.
- (3)
- If the entropic pair (or other entropic tuple) of a shear flow subsystem differs from the frames of reference that define the surrounding flow, including changes with time, then:
- (A)
- The shear flow subsystem may be harnessing negentropy from its external environment, either from the ambient flow field or by exploiting some other connection, but can only do so to the extent that these are harnessable by the subsystem.
- (B)
- Any excess entropy production, above what is actually harnessed from the external environment, reveals the existence of at least one independent source of negentropy for the shear flow subsystem.
5.2. Unsteady Internal Flows
6. Conclusions
- (1)(A)
- A shear flow subsystem at steady state, defined by fluid flow relative to a solid object, preferentially selects an entropic pair of inertial frames of reference, consisting of (i) the frame moving with the solid, i.e., that in which the solid is stationary, and (ii) the frame moving with the mean fluid flow, i.e., that in which the mean fluid flow is stationary. These frames are unique. They can be described as being entropically paired by the subsystem and inertially separated by their difference in velocities.
- (B)
- A shear flow subsystem at steady state, generated by the relative motion of two solid objects within a fluid, preferentially selects an entropic pair of inertial frames of reference, consisting of the frames moving with each solid.
- (C)
- A shear flow subsystem at steady state, defined by the relative motions of two solid objects and a fluid stream, or two fluid streams and a solid object, preferentially selects an entropic triple of inertial frames of reference, consisting of the frames moving with each solid and fluid flow. The entropic triple can be analyzed in terms of its three constituent entropic pairs.
- (D)
- A shear flow subsystem at steady state, defined by the relative motions of m independent solid objects and n independent fluid streams, preferentially selects an entropic -tuple of inertial frames of reference, consisting of the frames moving with each solid and fluid flow. The entropic -tuple can be analyzed in terms of its constituent entropic pairs.
- (E)
- A shear flow subsystem in unsteady flow, defined by the relative motions of a fluid and a solid, preferentially selects an entropic pair of frames of reference—or a set of entropic pairs—that is changing in time. At least one frame from each entropic pair will be a non-inertial frame of reference.
- (2)(A)
- An entropically paired shear flow subsystem must have at least one source of negentropy for its entropy production.
- (B)
- An entropically tripled shear flow subsystem must have at least two independent sources of negentropy for its entropy production.
- (C)
- An entropically -tupled shear flow subsystem must have at least independent sources of negentropy for its entropy production.
- (3)
- If the entropic pair (or other entropic tuple) of a shear flow subsystem differs from the frames of reference that define the surrounding flow, including changes with time, then:
- (A)
- The shear flow subsystem may be harnessing negentropy from its external environment, either from the ambient flow field or by exploiting some other connection, but can only do so to the extent that these are harnessable by the subsystem.
- (B)
- Any excess entropy production, above what is actually harnessed from the external environment, reveals the existence of at least one independent source of negentropy for the shear flow subsystem.
Funding
Acknowledgments
Conflicts of Interest
References
- Newton, I. Philosophiæ Naturalis Principia Mathematica; Joseph Streater, Royal Society: London, UK, 1687. [Google Scholar]
- Motte, A. Newton’s Principia, The Mathematical Principles of Natural Philosophy, 3rd ed.; Middle-Temple-Gate, Fleetstreet: London, UK, 1846; pp. 18–20. [Google Scholar]
- Wikipedia. Classical Mechanics. Available online: https://en.wikipedia.org/wiki/Classical_mechanics (accessed on 15 September 2021).
- Galileo, G.L. Dialogo Sopra i due Massimi Sistemi del Mondo; Per Gio Batifta Landini: Florence, Italy, 1632. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge Univ. Press: Cambridge, UK, 2000. [Google Scholar]
- Fourier, J.B.J. Théorie Analytique de la Chaleur; Didot: Paris, Framce, 1822. [Google Scholar]
- Rayleigh, J.W. The Theory of Sound; Macmillan and Co.: London, UK, 1877; Volume 1. [Google Scholar]
- Bertrand, J. Sur l’homogénéité dans les formules de physique. Comptes Rendus l’Acad. Sci. 1878, 86, 916–920. [Google Scholar]
- Rayleigh, J.W. On the question of the stability of the flow of liquids. Phil. Mag. 1892, 34, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Carvallo, E. Sur une similitude dans les fonctions des machines. J. Phys. Theor. Appl. 1892, 1, 209–212. [Google Scholar] [CrossRef]
- Vaschy, A. Théorie de l’Électricité: Exposé des Phénomènes Électriques et Magnétiques Fondé Uniquement sur L’expérience et le Raisonnement; Librairie Polytechnique, Baudry et Cie: Paris, France, 1892. [Google Scholar]
- Vaschy, A. Sur les lois de similitude en physique. Ann. Télégraphiques 1892, 19, 25–28. [Google Scholar]
- Federman, A. On some general methods of integration of first-order partial differential equations. Proc. St.-Petersburg Polytech. Inst. Sect. Tech. Nat. Sci. Math. 1911, 16, 97–155. [Google Scholar]
- Riabouchinsky, D. Méthode des variables de dimension zéro, et son application en aérodynamique. L’Aérophile 1911, 1, 407–408. [Google Scholar]
- Buckingham, E. On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Riabouchinsky, D. The principle of similitude. Nature 1915, 95, 591. [Google Scholar] [CrossRef]
- Langhaar, H.L. Dimensional Analysis and Theory of Models; John Wiley & Sons: New York, NY, USA, 1951. [Google Scholar]
- Zeldovich, Y.B. The motion of a gas under the action of a short term pressure (shock). Akust. Zhurnal 1956, 22, 28–38. [Google Scholar]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; Infosearch Ltd.: London, UK, 1959. [Google Scholar]
- Birkhoff, G. Hydrodynamics, a Study in Logic, Fact and Similitude, 2nd ed.; Princeton Univ. Press: Princeton, NJ, USA, 1960. [Google Scholar]
- Gratton, J. Similarity and self similarity in fluid dynamics. Fundam. Cosm. Phys. 1991, 15, 1–106. [Google Scholar]
- Barenblatt, G.I. Scaling, Self-Similarity and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics; Cambridge Univ. Press: Cambridge, UK, 1996. [Google Scholar]
- Barenblatt, G.I. Scaling; Cambridge Univ. Press: Cambridge, UK, 2003. [Google Scholar]
- Hornung, H.G. Dimensional Analysis: Examples of the Use of Symmetry; Dover Publ.: Mineola, NY, USA, 2006. [Google Scholar]
- Burde, G.I. Expanded Lie group transformations and similarity reductions of differential equations. Proc. Inst. Math. NAS Ukraine 2002, 43, 93–101. [Google Scholar]
- Oliveri, F. Lie symmetries of differential equations: Classical results and recent contributions. Symmetry 2010, 2, 658–706. [Google Scholar] [CrossRef] [Green Version]
- Ercan, A.; Kavvas, M.L. Self-similarity in incompressible Navier–Stokes equations. Chaos 2015, 25, 123126. [Google Scholar] [CrossRef] [PubMed]
- Polsinelli, J.; Kavvas, M.L. A comparison of the modern Lie scaling method to classical scaling techniques. Hydrol. Earth Syst. Sci. 2016, 20, 2669–2678. [Google Scholar] [CrossRef] [Green Version]
- Ercan, A.; Kavvas, M.L. Scaling relations and self-similarity of 3-dimensional Reynolds-averaged Navier–Stokes equations. Sci. Rep. 2017, 7, 6416. [Google Scholar] [CrossRef] [PubMed]
- She, Z.-S.; Chen, X.; Hussain, F. Quantifying wall turbulence via a symmetry approach: A Lie group theory. J. Fluid Mech. 2017, 827, 322–356. [Google Scholar] [CrossRef] [Green Version]
- Niven, R.K.; Noack, B.R. Control volume analysis, entropy balance and the entropy production in flow systems. In Beyond the Second Law: Entropy Production and Non-Equilibrium Systems; Dewar, R.C., Lineweaver, C., Niven, R.K., Regenauer-Lieb, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 129–162. [Google Scholar]
- Niven, R.K.; Ozawa, H. Entropy production extremum principles. In Handbook of Applied Hydrology, 2nd ed.; Singh, V., Ed.; McGraw-Hill: New York, NY, USA, 2016; Chapter 32; ISBN 978-0071835091. [Google Scholar]
- Jaumann, G. Geschlossenes System physikalischer und chemischer Differentialgesetze. Sitzungsberichte Akad. Der Wisenschaften Wien Math.—Naturwissenschaftliche Kl. 1911, 120, 385–530. [Google Scholar]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publ.: Mineola, NY, USA, 1962. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes, 3rd ed.; Interscience Publ.: New York, NY, USA, 1967. [Google Scholar]
- Kreuzer, H.J. Nonequilibrium Thermodynamics and its Statistical Foundations; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures, 2nd ed.; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Basaran, C. Introduction to Unified Mechanics Theory with Applications; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Bejan, A. Entropy Generation Through Heat and Fluid Flow; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Weinstock, R. Calculus of Variations; Dover Publ.: Mineola, NY, USA, 1952. [Google Scholar]
- Gelfand, I.M.; Fomin, S.V. Calculus of Variations; Dover Publ.: Mineola, NY, USA, 1963. [Google Scholar]
- Adeyinka, O.B.; Naterer, G.F. Modeling of entropy production in turbulent flows. J. Fluids Eng. 2004, 126, 893–899. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary Layer Theory, 8th ed.; Springer: New Delhi, India, 2001. [Google Scholar]
- Pao, H.F. Fluid Mechanics; John Wiley & Sons: New York, NY, USA, 1961. [Google Scholar]
- Street, R.L.; Watters, G.Z.; Vennard, J.K. Elementary Fluid Mechanics, 7th ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Streeter, V.L.; Wylie, E.B.; Bedford, K.W. Fluid Mechanics, 9th ed.; McGraw-Hill: Boston, MA, USA, 1998. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Munson, B.R.; Young, D.F.; Okiishi, T.H.; Huebsch, W.W. Fundamentals of Fluid Mechanics, 6th international student ed.; John Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Douglas, J.F.; Gasiorek, J.M.; Swaffield, J.A.; Jack, L.B. Fluid Mechanics, 6th ed.; Prentice Hall: Harlow, UK, 2011. [Google Scholar]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; Addison-Wesley: Reading, MA, USA, 1992. [Google Scholar]
- Lie, S.; Engel, F. Theorie der Transformationsgruppen; B.G. Teubner: Leipzig, Germany, 1888. [Google Scholar]
- Ovsainnikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Blumen, G.W.; Kumei, S. Symmetries and Differential Equations; Springer-Verlag: New York, NY, USA, 1989. [Google Scholar]
- Niven, R.K.; Cordier, L.; Kaiser, E.; Schlegel, M.; Noack, B.R. Rethinking the Reynolds transport theorem, Liouville equation, and Perron-Frobenius and Koopman operators. arXiv 2019, arXiv:1810.06022. [Google Scholar]
- Niven, R.K. New classes of conservation laws based on generalized fluid densities and Reynolds transport theorems. arXiv 2021, arXiv:2101.06113. [Google Scholar]
- Mohammadipoor, O.R.; Niazmand, H.; Mirbozorgi, S.A. Alternative curved-boundary treatment for the lattice Boltzmann method and its application in simulation of flow and potential fields. Phys. Rev. E 2014, 89, 013309. [Google Scholar] [CrossRef] [PubMed]
- Spurk, J.H. Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Academic Press, Inc.: New York, NY, USA, 1978. [Google Scholar]
- Pavlov, K.F.; Romankov, P.G.; Noskov, A.A. Examples and Problems to the Course of Unit Operations of Chemical Engineering; Mir Publ.: Moscow, Russia, 1979. [Google Scholar]
- Niven, R.K. Physical insight into the Ergun and Wen & Yu equations for fluid flow in packed and fluidised beds. Chem. Eng. Sci. 2002, 57, 527–534. [Google Scholar]
- Niven, R.K. Simultaneous extrema in the entropy production for steady-state fluid flow in parallel pipes. J. Non-Equil. Therm. 2010, 35, 347–378. [Google Scholar] [CrossRef] [Green Version]
- Waldrip, S.H.; Niven, R.K.; Abel, M.; Schlegel, M. Maximum entropy analysis of hydraulic pipe flow networks. J. Hydraul. Eng. ASCE 2016, 142, 04016028. [Google Scholar] [CrossRef]
- Waldrip, S.H.; Niven, R.K.; Abel, M.; Schlegel, M. Reduced-parameter method for maximum entropy analysis of hydraulic pipe flow networks. J. Hydraul. Eng. ASCE 2018, 144, 04017060. [Google Scholar] [CrossRef]
- Niven, R.K.; Abel, M.; Schlegel, M.; Waldrip, S.H. Maximum entropy analysis of flow networks: Theoretical foundation and applications. Entropy 2019, 21, 776. [Google Scholar] [CrossRef] [Green Version]
- Churchill, S.W. Viscous Flows—The Practical Use of Theory; Butterworths: Boston, MA, USA, 1988. [Google Scholar]
- Cheng, N.-S.; Chiew, Y.-M. Incipient sediment motion with upward seepage. J. Hydraul. Res. 1999, 37, 665–681. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. IChemE 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Paulus, D.M., Jr. Second Law Applications in Modeling, Design and Optimization. Ph.D. Thesis, Marquette University, Milwaukee, WI, USA, 2000. [Google Scholar]
- Paulus, D.M., Jr.; Gaggioli, R.A. Some Observations of Entropy Extrema in Fluid Flow. Energy 2004, 29, 2487–2500. [Google Scholar] [CrossRef]
- Martyushev, L.M. Some interesting consequences of the maximum entropy production principle. J. Exper. Theor. Phys. 2007, 104, 651–654. [Google Scholar] [CrossRef]
- Tait, P.G. Sketch of Thermodynamics; Edmonston and Douglas: Edinburgh, UK, 1868; p. 100. [Google Scholar]
- Schrödinger, E. What is Life? Cambridge Univ. Press: Cambridge, UK, 1944. [Google Scholar]
- Brillouin, L. The negentropy principle of information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Trans. Connecticut Acad. 1877, 3, 108–248. [Google Scholar] [CrossRef]
- Planck, M. Treatise on Thermodynamics, 3rd ed.; Dover Publ.: Mineola, NY, USA, 1922. [Google Scholar]
- Planck, M. Introduction to Theoretical Physics, Vol. V: Theory of Heat; Brose, H.L., Translator; Macmillan & Co., Ltd: London, UK, 1932. [Google Scholar]
- Schrödinger, E. Statistical Thermodynamics; Dover Publ.: Mineola, NY, USA, 1946. [Google Scholar]
- Keenan, J.H. Availability and irreversibility in thermodynamics. Brit. J. Appl. Phys. 1951, 2, 183–193. [Google Scholar] [CrossRef]
- Gaggioli, R.A. The concepts of thermodynamic friction, thermal available energy, chemical available energy and thermal energy. Chem. Eng. Sci. 1962, 17, 523–530. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Thermodynamics: An Advanced Treatment for Chemists and Physicists; North-Holland Publ. Co.: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Rant, Z. Exergie, ein neues Wort fur, technische Arbeitsfahigkeit. Forsch. Ingenieurwesen 1956, 22, 36–37. [Google Scholar]
- Evans, R.B. A Proof that Essergy is the Only Consistent Measure of Potential Work (for Chemical Substances). Ph.D. Thesis, Thayer School of Engineering, Dartmouth College, Hanover, NH, USA, 1969. [Google Scholar]
- Rajaratnam, N. Turbulent Jets; Elsevier Scientific: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Lee, J.H.W.; Chu, V.H. Turbulent Jets and Plumes—A Lagrangian Approach; Kluwer: Boston, MA, USA, 2003. [Google Scholar]
- Boussinesq, J.V. Sur la résistance qu’oppose un fluide indéfini au repos, sans pesanteur, au mouvement varié d’une sphère solide qu’il mouille sur toute sa surface, quand les vitesses restent bien continues et assez faibles pour que leurs carrés et produits soient négligeables. Comptes Rendus L’AcadÉmie Sci. 1885, 100, 935–937. [Google Scholar]
- Basset, A.B. A Treatise on Hydrodynamics; Deighton, Bell and Co.: Cambridge, UK, 1888; Volume 2, Chapter 22. [Google Scholar]
- Oseen, C.W. Hydrodynamik; Akademische Verlagsgesellschaft: Leipzig, Germany, 1927. [Google Scholar]
- Tchen, C.M. Mean Value and Correlation Problems Connected with the Motion of Small Particles Suspended in a Turbulent Fluid. Ph.D. Thesis, Technical School in Delft, Martinus Nijhoff, The Hague, The Netherlands, 1947. [Google Scholar]
- Corrsin, S.; Lumley, J. On the equation of motion for a particle in turbulent fluid. Appl. Sci. Res. 1956, A6, 114–116. [Google Scholar] [CrossRef]
- Odar, F.; Hamilton, W.S. Forces on a sphere accelerating in a viscous fluid. J. Fluid Mech. 1964, 18, 302–314. [Google Scholar] [CrossRef] [Green Version]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883–889. [Google Scholar] [CrossRef]
- Mei, R. Flow due to an oscillating sphere and an expression for unsteady drag on the sphere at finite Reynolds number. J. Fluid Mech. 1994, 270, 133–174. [Google Scholar] [CrossRef]
- Hohermuth, B.; Kramer, M.; Felder, S.; Valero, D. Velocity bias in intrusive gas-liquid flow measurements. Nat. Comm. 2021, 12, 4123. [Google Scholar] [CrossRef] [PubMed]
- Lukerchenko, N.; Kvurt, Y.; Keita, I.; Chara, Z.; Vlasak, P. Drag force, drag torque, and Magnus force coefficients of rotating spherical particle moving in fluid. Partic. Sci. Technol. 2012, 30, 55–67. [Google Scholar] [CrossRef]
- Sawatzki, O. Das Strömungsfeld um eine rotierende Kugel. Acta Mech. 1970, 9, 159–214. [Google Scholar] [CrossRef]
- Mittal, S.; Kumar, B. Flow past a rotating cylinder. J. Fluid Mech. 2003, 476, 303–334. [Google Scholar] [CrossRef] [Green Version]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, the Finite Volume Method, 2nd ed.; Pearson, Prentice Hall: Harlow, UK, 2007. [Google Scholar]
- Pettigrew, M.J.; Taylor, C.E.; Fisher, N.J.; Yetisir, M.; Smith, B.A.W. Flow-induced vibration: Recent findings and open questions. Nucl. Eng. Des. 1998, 185, 249–276. [Google Scholar] [CrossRef]
- Naudasher, E.; Rockwell, D. Flow-Induced Vibrations: An Engineering Guide; Dover Publ.: Mineola, NY, USA, 2005. [Google Scholar]
- Rajamuni, M.M.; Thompson, M.C.; Hourigan, K. Vortex dynamics and vibration modes of a tethered sphere. J. Fluid Mech. 2020, 885, A10. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics, international student edition; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Henderson, F.M. Open Channel Flow; Prentice Hall: Upper Saddle River, NJ, USA, 1966. [Google Scholar]
- Subramanya, K. Flow in Open Channels; Tata McGraw-Hill Publ. Co.: New Delhi, India, 1997. [Google Scholar]
- Reineck, H.-E.; Singh, I.B. Depositional Sedimentary Environments; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Niven, R.K. Steady state of a dissipative flow–controlled system and the maximum entropy production principle. Phys. Rev. E 2009, 80, 021113. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niven, R.K. Invariance Properties of the Entropy Production, and the Entropic Pairing of Inertial Frames of Reference by Shear-Flow Systems. Entropy 2021, 23, 1515. https://doi.org/10.3390/e23111515
Niven RK. Invariance Properties of the Entropy Production, and the Entropic Pairing of Inertial Frames of Reference by Shear-Flow Systems. Entropy. 2021; 23(11):1515. https://doi.org/10.3390/e23111515
Chicago/Turabian StyleNiven, Robert K. 2021. "Invariance Properties of the Entropy Production, and the Entropic Pairing of Inertial Frames of Reference by Shear-Flow Systems" Entropy 23, no. 11: 1515. https://doi.org/10.3390/e23111515
APA StyleNiven, R. K. (2021). Invariance Properties of the Entropy Production, and the Entropic Pairing of Inertial Frames of Reference by Shear-Flow Systems. Entropy, 23(11), 1515. https://doi.org/10.3390/e23111515




