Scheduling to Minimize Age of Incorrect Information with Imperfect Channel State Information
Abstract
:1. Introduction
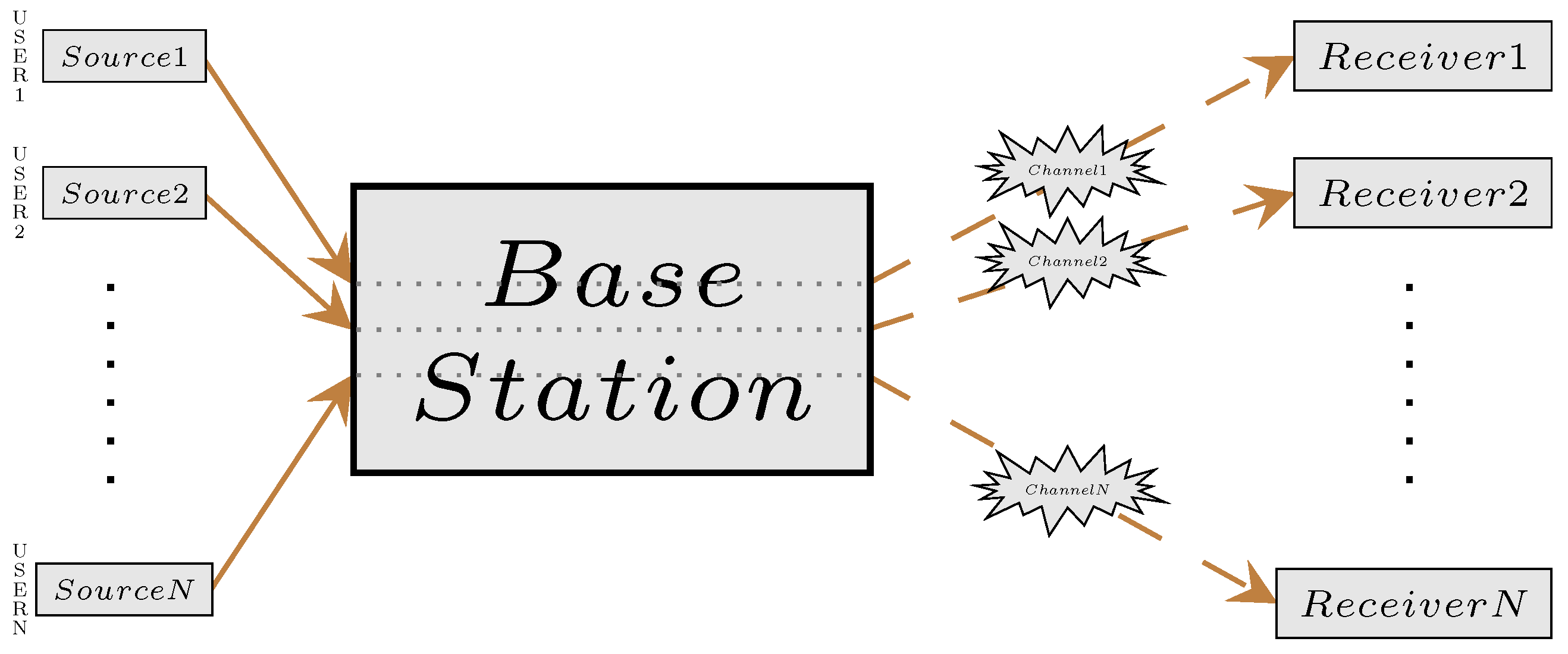
2. System Overview
2.1. Communication Model
2.2. Age of Incorrect Information
- When the receiver’s estimate is correct at time , we have . Then, by definition, .
- When the receiver’s estimate is incorrect at time , we have . Then, by definition, .
2.3. System Dynamic
- When , the estimate at time t is correct (i.e., ). Hence, for the receiver, carries no new information about the source process. In other words, regardless of whether an update is transmitted at time t. We recall that if and otherwise. Since the source is binary, we obtain if , which happens with probability p and otherwise. According to (2), we obtain
- When and , where , the channel will not be used and no new update will be received by the receiver, and so, . We recall that if and otherwise. Since and the source is binary, we have if , which happens with probability and otherwise. According to (2), we obtain
- When and where , the transmission attempt will succeed with probability and fail with probability . We recall that if and otherwise. Then, when the transmission attempt succeeds (i.e., ), if and otherwise. When the transmission attempt fails (i.e., ), we have if and otherwise. Combining (2) with the dynamic of the source process we obtain
- When and , where , following the same line, we obtain
2.4. Problem Formulation
3. Structural Properties of the Optimal Policy
- denotes the state space. The state is where .
- denotes the action space. The feasible action is where and . Note that the feasible actions are independent of the state and the time.
- denotes the state transition probabilities. We define as the probability that action at state will lead to state . It is calculated bywhere is the transition probability from to when the estimate of CSI is and action is taken. The values of can be obtained easily from the results in Section 2.3.
- denotes the instant cost. When the system is at state and action is taken, the instant cost is .
- if . The equality holds when or .
- is non-increasing in and is non-decreasing in when . At the same time, is independent of for any .
- if . The equality holds when or .
- is non-increasing in if and is non-decreasing in if when . We define and for .
- if , , and users j and k are statistically identical.
- Neither nor increases. In this case, both and become zero.
- Either or increases and the other becomes zero. We denote by the probability that only increases when . The notation for other cases is defined analogously. The probabilities can be obtained easily using the results in Section 2.3.
- Both and increase. We denote by the probability that both and increase when . is defined analogously. The probabilities can be obtained easily using the results in Section 2.3.
- The user i with or will not be chosen unless it is to break the tie.
- When user j is chosen at state , then for state , such that and for , the optimal choice must be in the set .
- When , we consider two states, and , which differ only in the value of . Specifically, . If user j is chosen at state and , the optimal choice at state will also be user j.
- When , we consider two states, and , which differ only in the value of . Specifically, . If user j is chosen at state and , the optimal choice at state will also be user j.
- When all users are statistically identical, the optimal choice at any time slot must be either the user with where or the user with where . Moreover,
- If , it is optimal to choose the user with .
- If , the optimal choice will switch from the user with to the user with when increases from 0 to solely.
- According to Property 5 of Theorem 1, we can conclude that it is optimal to choose user j when .
- To determine the optimal choice in the case of , we recall that the optimal choice will be user k (i.e., ) if and will be user j (i.e., ) if . At the same time, Property 4 of Theorem 1 tells us that is non-increasing in when users j and k are statistically identical. Therefore, we can conclude that the optimal choice will switch from user k to user j when increases from 0 to solely.
4. Whittle’s Index Policy
- We first formulate a relaxed version of PP and apply the Lagrangian approach.
- Then, we decouple the problem of minimizing the Lagrangian function into N decoupled problems, each of which only considers a single user. By casting the decoupled problem into an MDP, we investigate the structural properties and performance of the optimal policy.
- Leveraging the results above and under a simple condition, we establish the indexability of the decoupled problem.
- Finally, we obtain the expression of Whittle’s index by solving the Bellman equation.
4.1. Relaxed Problem
4.2. Decoupled Model
- The optimal policy can be fully captured by . More precisely, when the system is at state , it is optimal to make a transmission attempt only when .
- .
4.3. Indexability
4.4. Whittle’s Index Policy
- The first two properties can be verified by noting that and the equality holds when or . At the same time, is non-decreasing in .
- The third and fourth properties can be verified by noting that is non-decreasing in .
- For the last property, we first notice that when users j and k are statistically identical and . Then, the property can be verified by noting that is non-decreasing in both and .
5. Optimal Policy for Relaxed Problem
5.1. Optimal Policy for Single User
5.2. Optimal Policy for RP
- It is optimal for ;
- The resulting expected transmission rate is equal to M.
- Initialize and .
- Do and until .
- Run Bisection search on the interval until the tolerance is met.
6. Indexed Priority Policy
6.1. Primal-Dual Heuristic
- If , the base station will choose the M users with the largest among the users.
- If , these users are chosen by the base station. The base station will choose additional users with the smallest .
- According to Proposition 6, we can decompose the problem into N subproblems.
- For each subproblem, the threshold structure of the optimal policy is utilized to reduce the running time of RVI.
- As we will see later, the developed policy can be obtained directly from the result of RVI in practice.
6.2. Indexed Priority Policy
- State is where randomization happens (randomization happens when the actions suggested by the two optimal deterministic policies are different), and it has a value of and where is given by (12) and is the action suggested by at state .
- For other values of , we have and .
- Primal feasibility: the constraints in (13) are satisfied.
- Dual feasibility: and for all , , and i.
- Complementary slackness: and for all , , and i.
- Stationarity: the gradient of with respect to vanishes.
- For state such that and , we have . Therefore, .
- For state such that and , we have . Therefore, .
- For state such that and , we have . Therefore, .
- The first two properties can be verified by noting that and the equality holds when or . At the same time, is non-decreasing in .
- The third and fourth properties can be verified by noting that is non-decreasing in .
- For the last property, we first notice that when users j and k are statistically identical and . Then, the property can be verified by noting that is non-decreasing in both and .
7. Numerical Results
- The Greedy+ policy yields a smaller expected average AoII than that achieved by the Greedy policy. Recall that we obtained the Greedy+ policy by applying the structural properties detailed in Corollary 1. Therefore, simple applications of the structural properties of the optimal policy can improve the performance of scheduling policies.
- The Indexed priority policy has comparable performance to Whittle’s index policy in all the system settings considered. The two policies have their own advantages. The Indexed priority policy has a broader scope of application, while Whittle’s index policy has a lower computational complexity.
- The performance of the Indexed priority policy and Whittle’s index policy is better than that of the Greedy/Greedy+ policies and is not far from the performance of the RP-optimal policy. Recall that the performance of the RP-optimal policy forms a universal lower bound on the performance of all admissible policies for PP. Hence, we can conclude that both the Indexed priority policy and Whittle’s index policy achieve good performances.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 1
- We first consider the case of and . When and for any , we havewhere is the estimated value function of the state with at iteration (at the risk of abusing the notation, we use and to represent the value functions of two states that differ only in the value of ). Then, we getThe inequalities hold since and Lemma 1 are true at iteration by assumption. Therefore, we have when for any .For the case of where , we notice that . Then, for any , we obtainTherefore, when , we haveThe inequalities hold since and Lemma 1 is true at iteration by assumption. Combining with the case of , holds for any under any feasible action. Since and differ only in the value of and is non-decreasing in for , we can see that for any feasible . Then, by (A1), we can conclude that the lemma holds at iteration when and .
- When and , by replacing the ’s in the above case with ’s, we can achieve the same result.
- When and , we notice thatThen, leveraging the monotonicity of and , we can conclude with the same result.
Appendix B. Proof of Lemma 2
- It is obvious that for any , there always exists . Then, we obtainThe second equality follows from the definition of , the property of summation, and the assumption at iteration . The last equality follows from the variable renaming. Then, by the definition of statistically identical, we have , , and . Therefore, we can conclude that .
- Along the same lines, we can easily show that and for .
Appendix C. Proof of Theorem 1
- When , we can easily show that for any by noticing that the two possible actions with respect to user j (i.e., and ) are equivalent when . Since is a linear combination of ’s with non-negative coefficients, we can conclude that in this case.
- When and , for any , we haveThe inequality holds because of Lemma 1 and the fact that . We recall that is a linear combination of ’s with non-negative coefficients. Then, we can conclude that in this case.
- When and , by replacing the in (A6) with , we can get the same result. In this case, the equality holds when , or, equivalently, .
- When , we have for any . Thus, we conclude that for any . Consequently, for any .
- When and , for any , we haveThe inequality follows from Lemma 1 and the fact that . Thus, for any .
- When and , by replacing the in (A7) with , we can get the same result. In this case, the equality holds when , or, equivalently, .
- In the case of and , for any , (A5) can be written asAs we can verifyWe define and for . Then, we haveCombining with Lemma 1, we can conclude that, for any , is non-increasing in if and is non-decreasing in if .
- In the case of and , by replacing the ’s in the above case with ’s, we can conclude with the same result.
- In the case of , , and , for any , (A5) can be written asAs we can verifyAt the same timeCombined with Lemma 1, we can conclude that, for any , is non-increasing in if and is non-decreasing in if .
- In the case of , , and , by swapping the ’s and ’s in the above case, we can conclude with the same result.
- We first consider the case of and . Leveraging the definition of statistically identical, for any , we havewhere . Then, by substituting the values of and using Lemma 2, we obtainSince users j and k are statistically identical, we have . Then, by Lemma 1, we have for any . Since is a linear combination of ’s with non-negative coefficients, we can conclude that .
- For the case of and , by replacing in with , we can conclude with the same result.
- Then, we consider the case of , , and . We first notice that, for anyAs users j and k are statistically identical, we have and . Leveraging Lemma 1, we haveThen, for anywhere . Such as we did in the previous cases, we can leverage Lemmas 1 and 2 to conclude that for any . Consequently, in this case. The details are omitted for the sake of space.
Appendix D. Proof of Corollary 2
- We first consider the case of and . When , we haveSubtracting the two expressions yieldsThe inequalities hold since , is non-decreasing in s, and Corollary 2 is true at iteration by assumption.For the case of , we obtainTherefore, when , we haveThe inequalities hold since , is non-decreasing in s, and Corollary 2 is true at iteration by assumption. Combined together, we can see that for any feasible a. Then, by problem (A8), we can conclude that the lemma holds at iteration when and .
- When and , by replacing the ’s in the above case with ’s, we can achieve the same result.
- When and , we notice that and . Then, leveraging the monotonicity of and , we can conclude with the same result.
Appendix E. Proof of Proposition 1
- Therefore, . Thus, the optimal action at state is .
- Then,where .
- Finally, we consider the state where . Following the same trajectory, we have
Appendix F. Proof of Proposition 2

- For state where , it is optimal to stay idle (i.e., ).
- For state where , it is optimal to make a transmission attempt only when . We recall that is an independent Bernoulli random variable with parameter . Therefore, the expected proportion of time that the system is at state is .
- For state where , it is optimal to make transmission attempt regardless of .
Appendix G. Proof of Proposition 4
- We first consider the state . By definition, Whittle’s index is the infimum such that . According to (A10), we can conclude that when .
- Then, we consider the state where . We recall that . Then, we can conclude, from (A11), that for all where .
Appendix H. Proof of Proposition 5
- For state where , by definition. As the problem is indexable, we have . We recall that . Equivalently, . Then, we know . Combined together, we conclude that . In other words, the optimal action at state where is to stay idle (i.e., ).
- For state where , we first recall that . Consequently, for any , we know . Meanwhile, we have by the monotonicity of Whittle’s index and the definition of n. Hence, we can conclude that . In other words, the optimal action at state where is to make the transmission attempt.
Appendix I. Proof of Theorem 2
- The probability where is the state of at time n.
- The expected time of a first passage from i to G under is finite.
- The expected -cost and the expected -cost of a first passage form i to G under are finite.
- For all , the set there exists an action a such that is finite: For any state x, the cost satisfies . The equality holds when . Then, the states in must satisfy . Combined with the fact that is a non-decreasing and unbounded function when , we can conclude that is finite.
- There exists a stationary policy e such that the induced Markov chain has the following properties: the state space consists of a single (non-empty) positive recurrent class R and a set U of transient states such that for . Moreover, both and on R are finite: We consider the policy under which the base station makes a transmission attempt at every time slot. According to the system dynamic detailed in Section 2.3, we can see that all the states communicate with state and communicates with all other states. Thus, the state space consists of a single (non-empty) positive recurrent class and the set of transient states can simply be an empty set. and are trivially finite as we can verify using Proposition 2.
- Given any two state , there exists a policy ϕ such that : We notice that, under any policy, the maximum increase of s between two consecutive time slots is 1. Meanwhile, when s decreases, it decreases to zero. Combined with the fact that is an independent Bernoulli random variable, we can conclude that there always exists a path between any x and y with positive probability. , , and are trivially finite.
- If a stationary policy ϕ has at least one positive recurrent state, then it has a single positive recurrent class R. Moreover, if , then : Given that is an independent Bernoulli random variable, we can easily conclude from the system dynamic that all the states communicate with state and communicates with all other states under any stationary policy. Therefore, any positive recurrent class must contain state . Thus, there must have only one positive recurrent class which is .
- There exists a policy ϕ such that and where : We notice that and are nothing but the expected AoII and the expected transmission rate achieved by , respectively. Then, we can easily verify that such policy exists using Proposition 2.
Appendix J. Proof of Proposition 6
Appendix K. Proof of Theorem 3
- It is -optimal;
- The resulting expected transmission rate is equal to M.
- For user i with , the threshold policy is used. Then, the deterministic policy is optimal for andIn this case, the choice of makes no difference.
- For user i with , the randomized policy as detailed in Theorem 2 is used. Then, for any , the randomized policy is optimal for and
Appendix L. Proof of Proposition 8
- For state , .
- For state where , where .
- For state where , .
Appendix M
| Algorithm A1 Improved Relative Value Iteration | |
| Require: | |
| MDP | |
| Convergence Criteria | |
| 1: | procedureRelativeValueIteration(,) |
| 2: | Initialize ; |
| 3: | Choose arbitrarily |
| 4: | while is not converged (RVI converges when the maximum difference between the results of two consecutive iterations is less than ) do |
| 5: | for do |
| 6: | if ∃ active state s.t. and then |
| 7: | |
| 8: | |
| 9: | else |
| 10: | for do |
| 11: | |
| 12: | |
| 13: | |
| 14: | for do |
| 15: | |
| 16: | |
| return | |
| Algorithm A2 Bisection Search | |
| Require: | |
| Maximum updates per transmission attempt M | |
| MDP | |
| Tolerance | |
| Convergence criteria | |
| 1: | procedureBisectionSearch(, M, , ) |
| 2: | Initialize ; |
| 3: | using Section 5.1 and Proposition 6 |
| 4: | using Proposition 2 |
| 5: | while do |
| 6: | ; |
| 7: | using Section 5.1 and Proposition 6 |
| 8: | using Proposition 2 |
| 9: | while do |
| 10: | |
| 11: | using Section 5.1 and Proposition 6 |
| 12: | using Proposition 2 |
| 13: | if then |
| 14: | |
| 15: | else |
| 16: | |
| return | |
References
- Maatouk, A.; Kriouile, S.; Assaad, M.; Ephremides, A. The age of incorrect information: A new performance metric for status updates. IEEE/ACM Trans. Netw. 2020, 28, 2215–2228. [Google Scholar] [CrossRef]
- Uysal, E.; Kaya, O.; Ephremides, A.; Gross, J.; Codreanu, M.; Popovski, P.; Assaad, M.; Liva, G.; Munari, A.; Soleymani, T.; et al. Semantic communications in networked systems. arXiv 2021, arXiv:2103.05391. [Google Scholar]
- Kam, C.; Kompella, S.; Ephremides, A. Age of incorrect information for remote estimation of a binary markov source. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 6–9 July 2020; pp. 1–6. [Google Scholar]
- Maatouk, A.; Assaad, M.; Ephremides, A. The age of incorrect information: An enabler of semantics-empowered communication. arXiv 2020, arXiv:2012.13214. [Google Scholar]
- Chen, Y.; Ephremides, A. Minimizing Age of Incorrect Information for Unreliable Channel with Power Constraint. arXiv 2021, arXiv:2101.08908. [Google Scholar]
- Kriouile, S.; Assaad, M. Minimizing the Age of Incorrect Information for Real-time Tracking of Markov Remote Sources. arXiv 2021, arXiv:2102.03245. [Google Scholar]
- Kadota, I.; Sinha, A.; Uysal-Biyikoglu, E.; Singh, R.; Modiano, E. Scheduling policies for minimizing age of information in broadcast wireless networks. IEEE/ACM Trans. Netw. 2018, 26, 2637–2650. [Google Scholar] [CrossRef] [Green Version]
- Hsu, Y.P. Age of information: Whittle index for scheduling stochastic arrivals. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 2634–2638. [Google Scholar]
- Tripathi, V.; Modiano, E. A whittle index approach to minimizing functions of age of information. In Proceedings of the 2019 57th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 24–27 September 2019; pp. 1160–1167. [Google Scholar]
- Maatouk, A.; Kriouile, S.; Assad, M.; Ephremides, A. On the optimality of the Whittle’s index policy for minimizing the age of information. IEEE Trans. Wirel. Commun. 2020, 20, 1263–1277. [Google Scholar] [CrossRef]
- Sun, J.; Jiang, Z.; Krishnamachari, B.; Zhou, S.; Niu, Z. Closed-form Whittle’s index-enabled random access for timely status update. IEEE Trans. Commun. 2019, 68, 1538–1551. [Google Scholar] [CrossRef]
- Nguyen, G.D.; Kompella, S.; Kam, C.; Wieselthier, J.E. Information freshness over a Markov channel: The effect of channel state information. Ad Hoc Networks 2019, 86, 63–71. [Google Scholar] [CrossRef]
- Talak, R.; Karaman, S.; Modiano, E. Optimizing age of information in wireless networks with perfect channel state information. In Proceedings of the 2018 16th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Shanghai, China, 7–11 May 2018; pp. 1–8. [Google Scholar]
- Shi, L.; Cheng, P.; Chen, J. Optimal periodic sensor scheduling with limited resources. IEEE Trans. Autom. Control 2011, 56, 2190–2195. [Google Scholar] [CrossRef]
- Leong, A.S.; Dey, S.; Quevedo, D.E. Sensor scheduling in variance based event triggered estimation with packet drops. IEEE Trans. Autom. Control 2016, 62, 1880–1895. [Google Scholar] [CrossRef] [Green Version]
- Mo, Y.; Garone, E.; Casavola, A.; Sinopoli, B. Stochastic sensor scheduling for energy constrained estimation in multi-hop wireless sensor networks. IEEE Trans. Autom. Control 2011, 56, 2489–2495. [Google Scholar] [CrossRef] [Green Version]
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update? In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 2731–2735. [Google Scholar]
- Leong, A.S.; Ramaswamy, A.; Quevedo, D.E.; Karl, H.; Shi, L. Deep reinforcement learning for wireless sensor scheduling in cyber–physical systems. Automatica 2020, 113, 108759. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Ren, X.; Mo, Y.; Shi, L. Whittle index policy for dynamic multichannel allocation in remote state estimation. IEEE Trans. Autom. Control 2019, 65, 591–603. [Google Scholar] [CrossRef]
- Gittins, J.; Glazebrook, K.; Weber, R. Multi-Armed Bandit Allocation Indices; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall Press: Hoboken, NJ, USA, 2009. [Google Scholar]
- Whittle, P. Restless bandits: Activity allocation in a changing world. J. Appl. Probab. 1988, 25, 287–298. [Google Scholar] [CrossRef]
- Weber, R.R.; Weiss, G. On an index policy for restless bandits. J. Appl. Probab. 1990, 27, 637–648. [Google Scholar] [CrossRef]
- Glazebrook, K.D.; Ruiz-Hernandez, D.; Kirkbride, C. Some indexable families of restless bandit problems. Adv. Appl. Probab. 2006, 38, 643–672. [Google Scholar] [CrossRef]
- Larrañaga, M. Dynamic Control of Stochastic and Fluid Resource-Sharing Systems. Ph.D. Thesis, Université de Toulouse, Toulouse, France, 2015. [Google Scholar]
- Sennott, L.I. On computing average cost optimal policies with application to routing to parallel queues. Math. Methods Oper. Res. 1997, 45, 45–62. [Google Scholar] [CrossRef]
- Sennott, L.I. Constrained average cost Markov decision chains. Probab. Eng. Inf. Sci. 1993, 7, 69–83. [Google Scholar] [CrossRef]
- Bertsimas, D.; Niño-Mora, J. Restless bandits, linear programming relaxations, and a primal-dual index heuristic. Oper. Res. 2000, 48, 80–90. [Google Scholar] [CrossRef] [Green Version]
- Littman, M.L.; Dean, T.L.; Kaelbling, L.P. On the complexity of solving Markov decision problems. arXiv 2013, arXiv:1302.4971. [Google Scholar]
- Verloop, I.M. Asymptotically optimal priority policies for indexable and nonindexable restless bandits. Ann. Appl. Probab. 2016, 26, 1947–1995. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Ephremides, A. Scheduling to Minimize Age of Incorrect Information with Imperfect Channel State Information. Entropy 2021, 23, 1572. https://doi.org/10.3390/e23121572
Chen Y, Ephremides A. Scheduling to Minimize Age of Incorrect Information with Imperfect Channel State Information. Entropy. 2021; 23(12):1572. https://doi.org/10.3390/e23121572
Chicago/Turabian StyleChen, Yutao, and Anthony Ephremides. 2021. "Scheduling to Minimize Age of Incorrect Information with Imperfect Channel State Information" Entropy 23, no. 12: 1572. https://doi.org/10.3390/e23121572
APA StyleChen, Y., & Ephremides, A. (2021). Scheduling to Minimize Age of Incorrect Information with Imperfect Channel State Information. Entropy, 23(12), 1572. https://doi.org/10.3390/e23121572





