Bayesian and Classical Inference under Type-II Censored Samples of the Extended Inverse Gompertz Distribution with Engineering Applications
Abstract
:1. Introduction
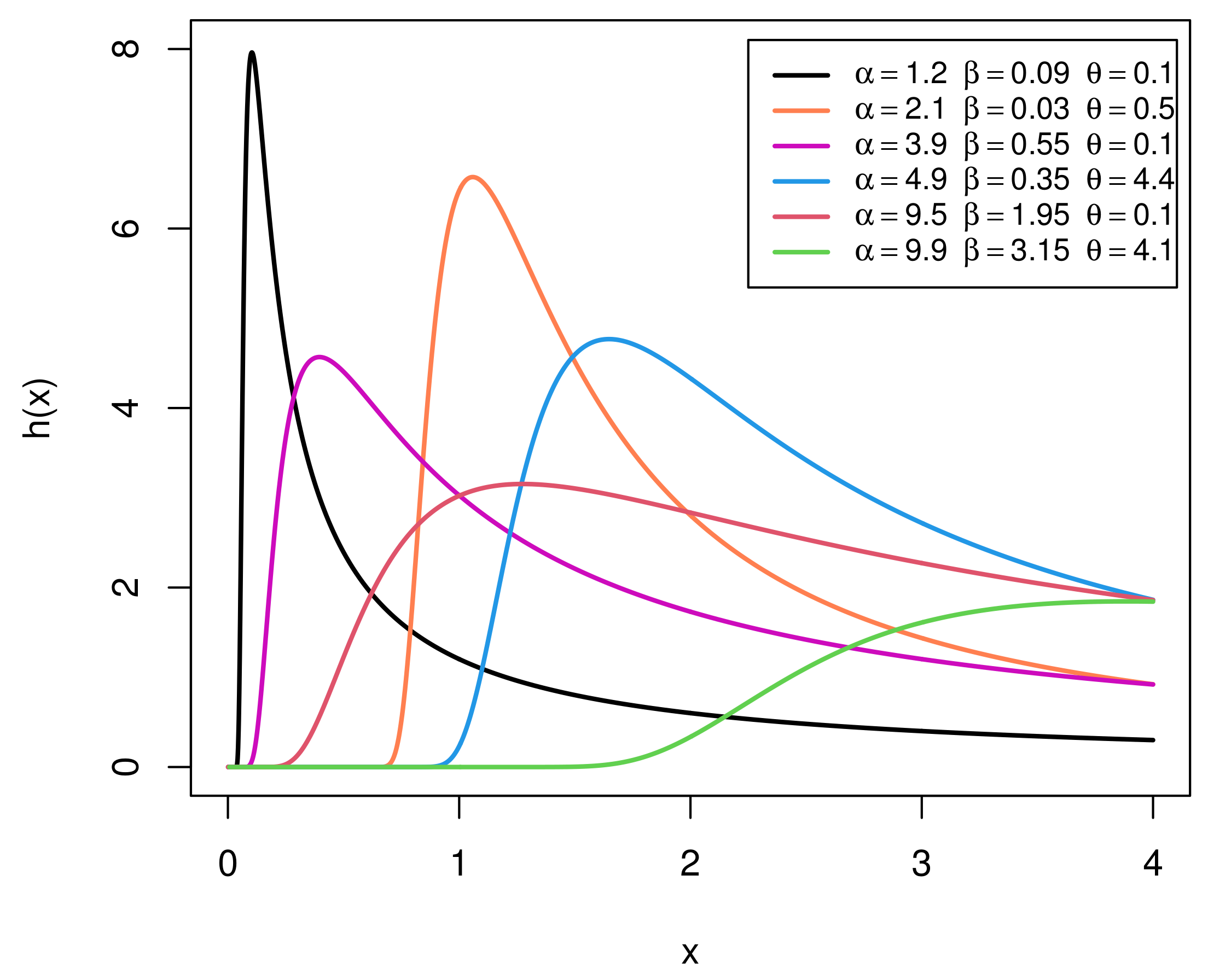
2. The EIGo Distribution
- The generalized inverted-exponential (GIE) distribution [20] follows when the parameter .
- The IGo distribution [18] is derived for .
- The inverse-exponential (IE) distribution [21] with one parameter can be derived when and .
Expansions
3. Statistical and Reliability Characteristics
3.1. Quantile and Mode
3.2. Mean Residual Life
3.3. Mean Inactivity Time
3.4. Strong MIT
3.5. Stress–Strength Reliability
3.6. Probability Weighted Moments
3.7. Moments
3.8. Entropies
3.9. Order Statistics
3.10. Stochastic Ordering
4. Parameter Estimation under Type-II Censoring
4.1. Maximum Likelihood Estimators
4.2. Bayes Estimators
5. Simulation Results
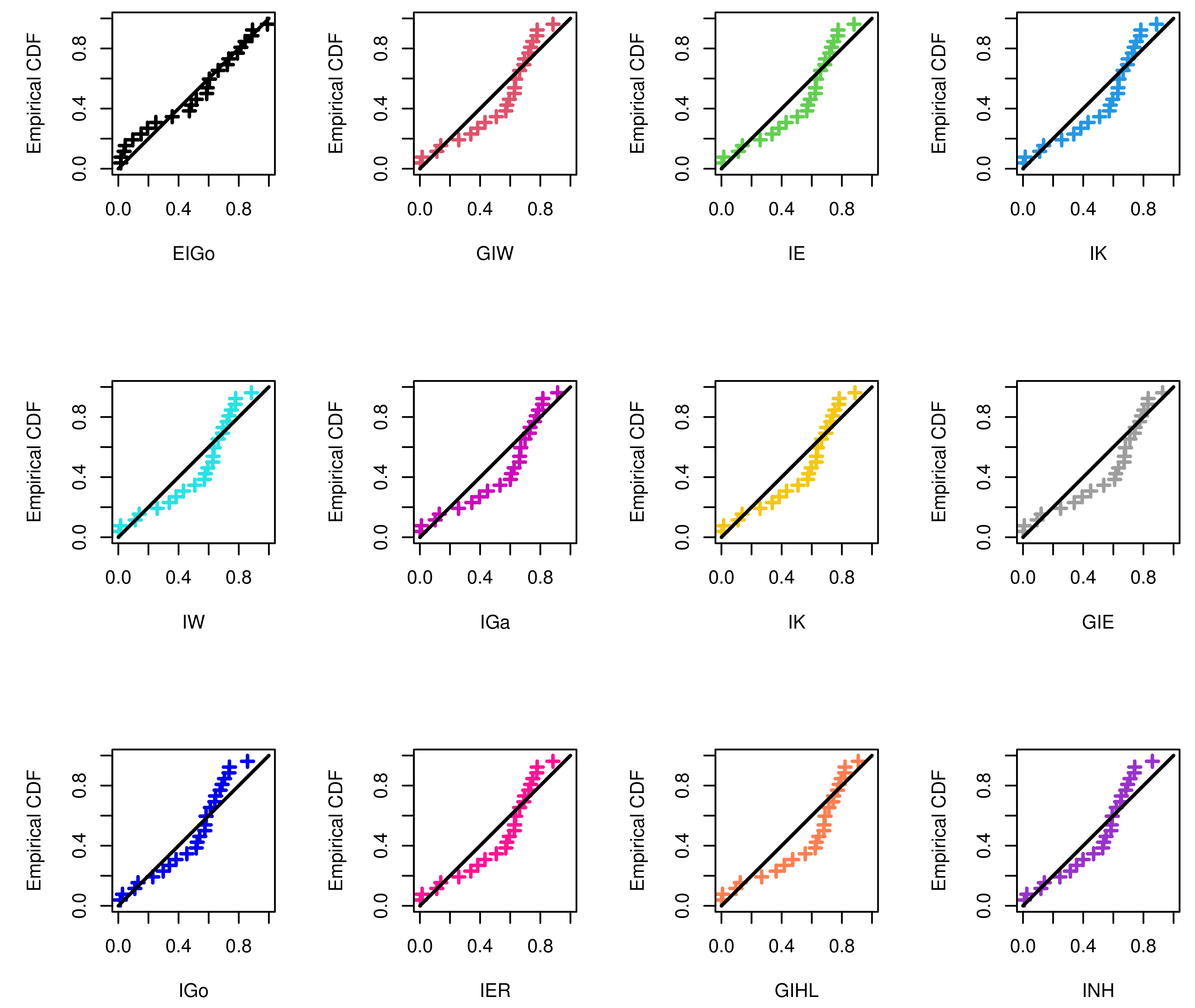
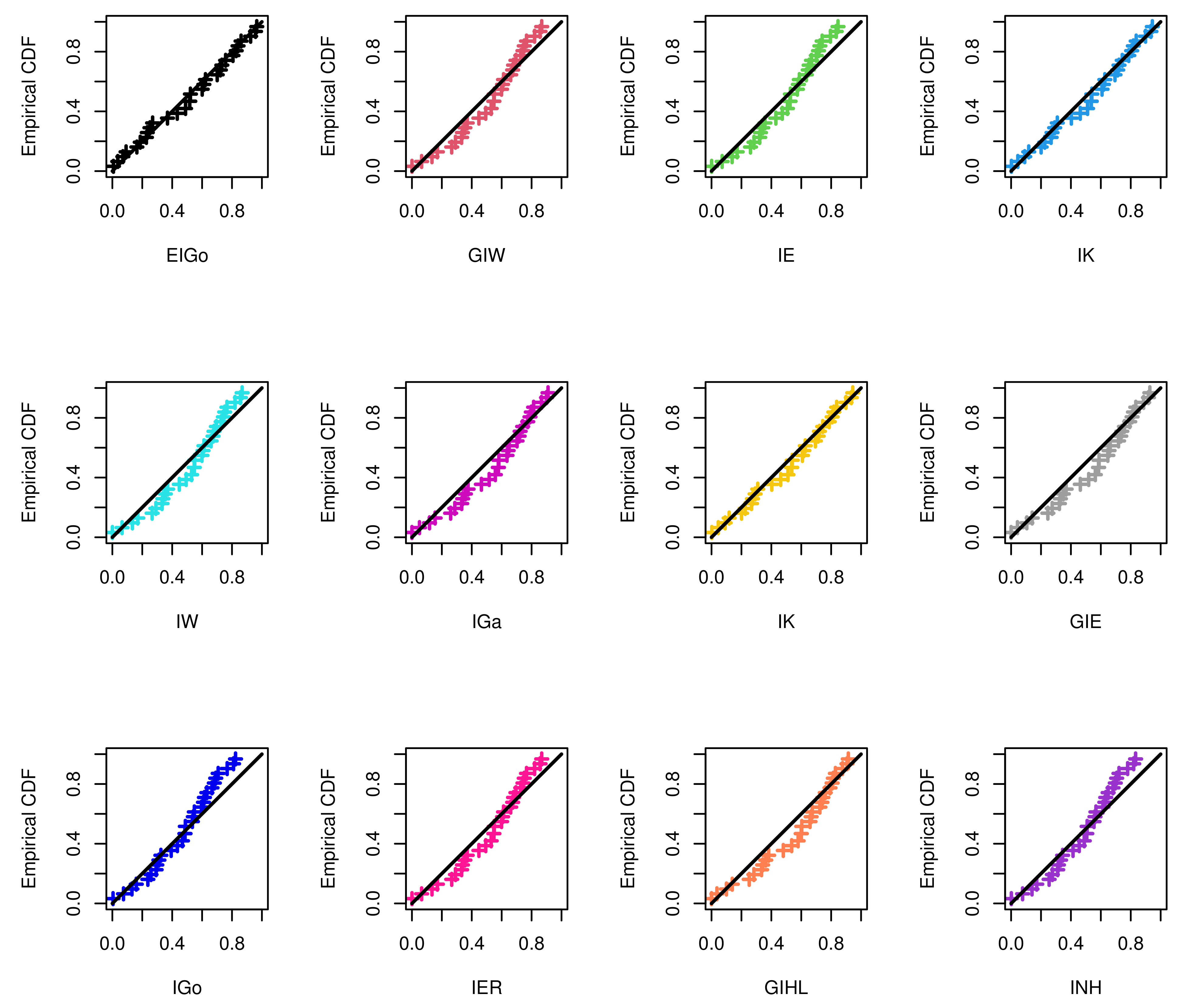
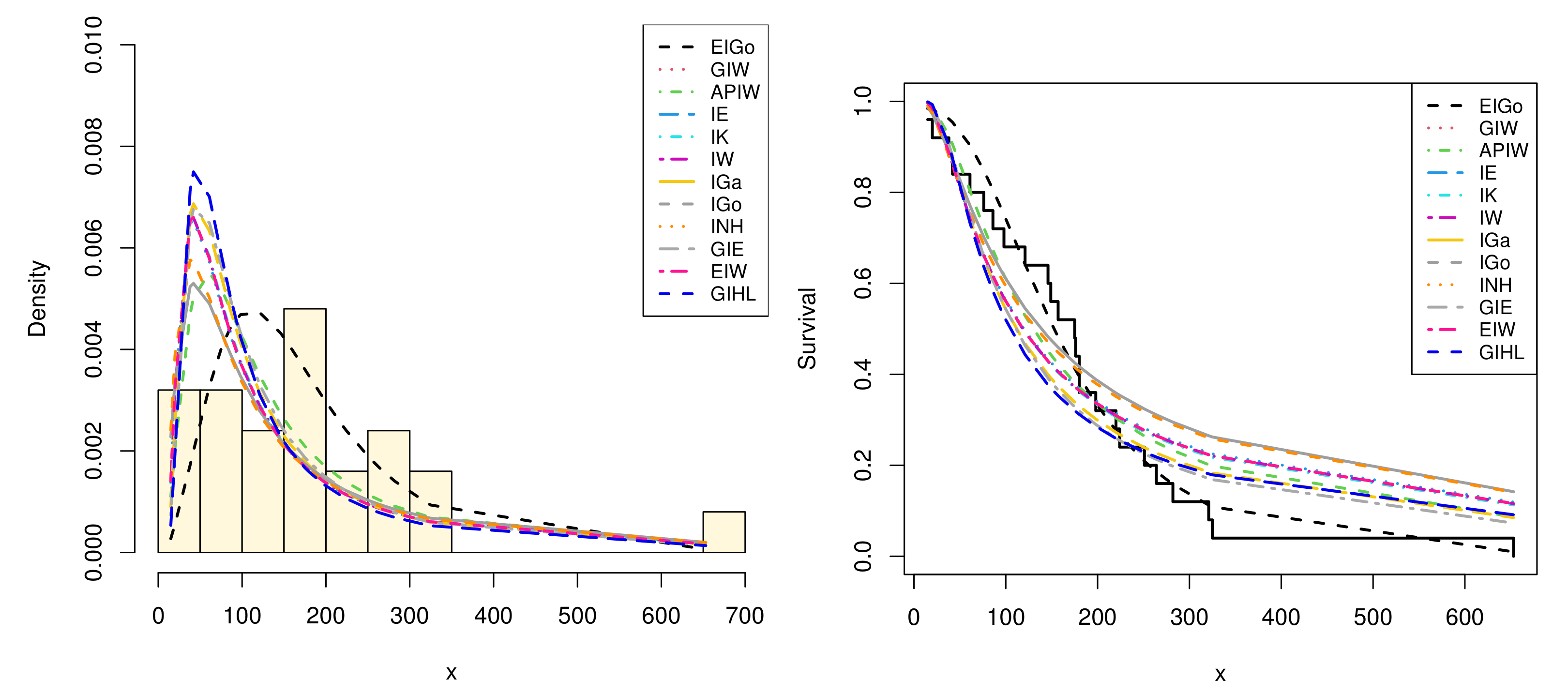
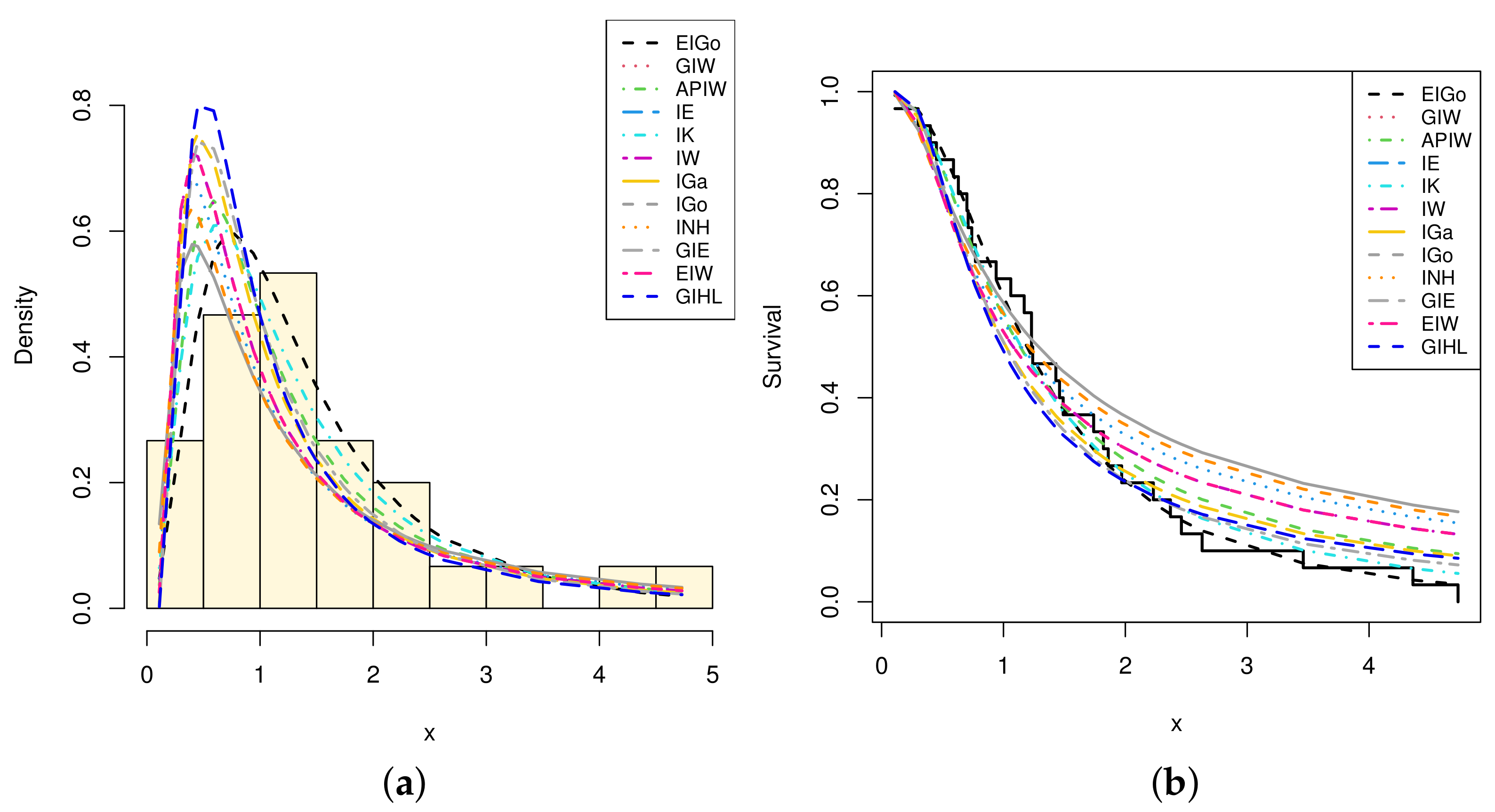
6. Real-Life Applications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. In A letter to Francis Baily, Esq. FRS & C. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar]
- El-Gohary, A.; Alshamrani, A.; Al-Otaibi, A.N. The generalized Gompertz distribution. Appl. Math. Model. 2013, 37, 13–24. [Google Scholar] [CrossRef] [Green Version]
- Jafari, A.A.; Tahmasebi, S.; Alizadeh, M. The beta-Gompertz distribution. Rev. Colomb. Estadística 2014, 37, 141–158. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Robert, K.; Irene, L.H. Transmuted Gompertz distribution: Properties and estimation. Pak. J. Stat. 2016, 32, 161–182. [Google Scholar]
- Roozegar, R.; Tahmasebi, S.; Jafari, A.A. The McDonald Gompertz distribution: Properties and applications. Commun. Stat.-Simul. Comput. 2017, 46, 3341–3355. [Google Scholar] [CrossRef] [Green Version]
- El-Bassiouny, A.H.; El-Damcese, M.; Mustafa, A.; Eliwa, M.S. Exponentiated generalized Weibull-Gompertz distribution with application in survival analysis. J. Stat. Appl. Probab 2017, 6, 7–16. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.; Dey, S. Unit-Gompertz distribution with applications. Statistica 2019, 79, 25–43. [Google Scholar]
- Ieren, T.G.; Kromtit, F.M.; Agbor, B.U.; Eraikhuemen, I.B.; Koleoso, P.O. A power Gompertz distribution: Model, properties and application to bladder cancer data. Asian Res. J. Math. 2019, 15, 1–14. [Google Scholar] [CrossRef]
- Hoseinzadeh, A.; Maleki, M.; Khodadadi, Z.; Contreras-Reyes, J.E. The skew-reflected-Gompertz distribution for analyzing symmetric and asymmetric data. J. Comput. Appl. Math. 2019, 349, 132–141. [Google Scholar] [CrossRef]
- Nzei, L.C.; Eghwerido, J.T.; Ekhosuehi, N. Topp-Leone Gompertz Distribution: Properties and Applications. J. Data Sci. 2020, 18, 782–794. [Google Scholar] [CrossRef]
- Eghwerido, J.T.; Nzei, L.C.; Agu, F.I. The alpha power Gompertz distribution: Characterization, properties, and applications. Sankhya A 2021, 83, 449–475. [Google Scholar] [CrossRef]
- Wu, J.W.; Hung, W.L.; Tsai, C.H. Estimation of parameters of the Gompertz distribution using the least squares method. Appl. Math. Comput. 2004, 158, 133–147. [Google Scholar] [CrossRef]
- Soliman, A.A.; Abd-Ellah, A.H.; Abou-Elheggag, N.A.; Abd-Elmougod, G.A. Estimation of the parameters of life for Gompertz distribution using progressive first-failure censored data. Comput. Stat. Data Anal. 2012, 56, 2471–2485. [Google Scholar] [CrossRef]
- Dey, S.; Moala, F.A.; Kumar, D. Statistical properties and different methods of estimation of Gompertz distribution with application. J. Stat. Manag. Syst. 2018, 21, 839–876. [Google Scholar] [CrossRef]
- Louzada, F.; Ramos, P.L.; Nascimento, D. The inverse Nakagami-m distribution: A novel approach in reliability. IEEE Trans. Reliab. 2018, 67, 1030–1042. [Google Scholar] [CrossRef]
- Ramos, P.L.; Louzada, F.; Shimizu, T.K.; Luiz, A.O. The inverse weighted Lindley distribution: Properties, estimation, and an application on a failure time data. Commun. Stat.-Theory Methods 2019, 48, 2372–2389. [Google Scholar] [CrossRef]
- Afify, A.Z.; Ahmed, S.; Nassar, M. A new inverse Weibull distribution: Properties, classical and Bayesian estimation with applications. Kuwait J. Sci. 2021, 48, 1–10. [Google Scholar] [CrossRef]
- Eliwa, M.S.; El-Morshedy, M.; Ibrahim, M. Inverse Gompertz distribution: Properties and different estimation methods with application to complete and censored data. Ann. Data Sci. 2019, 6, 321–339. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. The exponentiated type distributions. Acta Appl. Math. 2006, 92, 97–111. [Google Scholar] [CrossRef]
- Abouammoh, A.M.; Alshingiti, A.M. Reliability estimation of generalized inverted exponential distribution. J. Stat. Comput. Simul. 2009, 79, 1301–1315. [Google Scholar] [CrossRef]
- Keller, A.Z.; Kamath, A.R.R.; Perera, U.D. Reliability analysis of CNC machine tools. Reliab. Eng. 1982, 3, 449–473. [Google Scholar] [CrossRef]
- Jeong, J.H. Statistical Inference on Residual Life; Springer: New York, NY, USA, 2014. [Google Scholar]
- Kayid, M.; Izadkhah, S. Mean inactivity time function, associated orderings, and classes of life distributions. IEEE Trans. Reliab. 2014, 63, 593–602. [Google Scholar] [CrossRef]
- Johnson, R.A. Stress-Strength Models for Reliability. In Handbook of Statistics; Krishnaiah, P.R., Rao, C.R., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; Volume 7, pp. 27–54. [Google Scholar]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef] [Green Version]
- Lazo, A.V.; Rathie, P. On the entropy of continuous probability distributions. IEEE Trans. Inf. Theory 1978, 24, 120–122. [Google Scholar] [CrossRef]
- David, H.A.; Nagaraja, H.N. Order Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders and Their Applications; Academic Press: Boston, MA, USA, 1994. [Google Scholar]
- Lawless, J.F. Statistical Models and Methods For Lifetime Data, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kundu, D. Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics 2008, 50, 144–154. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Lynch, S.M. Introduction to Applied Bayesian Statistics and Estimation for Social Scientists; Springer: New York, NY, USA, 2007. [Google Scholar]
- Tierney, L. Markov chains for exploring posterior distributions. Ann. Stat. 1994, 22, 1701–1728. [Google Scholar] [CrossRef]
- Roberts, G.O.; Gelman, A.; Gilks, W.R. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Probab. 1997, 7, 110–120. [Google Scholar]
- Elshahhat, A.; Elemary, B.R. Analysis for Xgamma parameters of life under Type-II adaptive progressively hybrid censoring with applications in engineering and chemistry. Symmetry 2021, 13, 2112. [Google Scholar] [CrossRef]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Keller, A.Z.; Goblin, M.T.; Farnworth, N.R. Reliability analysis of commercial vehicle engines. Reliab. Eng. 1985, 10, 15–25. [Google Scholar] [CrossRef]
- Glen, A.G. On the inverse gamma as a survival distribution. J. Qual. Technol. 2011, 43, 158–166. [Google Scholar] [CrossRef]
- Gusmão, F.R.; Ortega, E.M.; Cordeiro, G.M. The generalized inverse Weibull distribution. Stat. Pap. 2011, 52, 591–619. [Google Scholar] [CrossRef]
- Flaih, A.; Elsalloukh, H.; Mendi, E.; Milanova, M. The exponentiated inverted Weibull distribution. Appl. Math. Inf. Sci. 2012, 6, 167–171. [Google Scholar]
- Potdar, K.G.; Shirke, D.T. Inference for the parameters of generalized inverted family of distributions. ProbStat Forum 2013, 6, 18–28. [Google Scholar]
- Abd AL-Fattah, A.M.; El-Helbawy, A.A.; Al-Dayian, G.R. Inverted Kumaraswamy distribution: Properties and estimation. Pak. J. Stat. 2017, 33, 37–61. [Google Scholar]
- Tahir, M.H.; Cordeiro, G.M.; Ali, S.; Dey, S.; Manzoor, A. The inverted Nadarajah–Haghighi distribution: Estimation methods and applications. J. Stat. Comput. Simul. 2018, 88, 2775–2798. [Google Scholar] [CrossRef]
- Basheer, A.M. Alpha power inverse Weibull distribution with reliability application. J. Taibah Univ. Sci. 2019, 13, 423–432. [Google Scholar] [CrossRef] [Green Version]

| n | m | MLE | MCMC | ||
|---|---|---|---|---|---|
| Prior (1) | Prior (2) | ||||
| (0.5,0.1,0.1) | 40 | 40 | 0.5175 (0.1327,0.1993) | 0.5013 (0.0856,0.1338) | 0.4884 (0.0728,0.1164) |
| 30 | 0.4516 (0.1910,0.3075) | 0.4096 (0.1456,0.2435) | 0.4150 (0.1356,0.2265) | ||
| 20 | 0.4109 (0.3225,0.4847) | 0.2941 (0.2414,0.4326) | 0.3505 (0.2135,0.3660) | ||
| 60 | 60 | 0.5149 (0.1099,0.1693) | 0.4888 (0.0618,0.0922) | 0.4954 (0.0607,0.0973) | |
| 45 | 0.4356 (0.1776,0.2799) | 0.4034 (0.1391,0.2321) | 0.4112 (0.1343,0.2214) | ||
| 30 | 0.4010 (0.2607,0.4204) | 0.2959 (0.2366,0.4219) | 0.3217 (0.2214,0.3847) | ||
| 80 | 80 | 0.5086 (0.0892,0.1373) | 0.5117 (0.0592,0.0919) | 0.5048 (0.0572,0.0901) | |
| 60 | 0.4369 (0.1671,0.2445) | 0.4015 (0.1368,0.2264) | 0.4034 (0.1346,0.2221) | ||
| 40 | 0.3924 (0.2393,0.3845) | 0.3129 (0.2263,0.3957) | 0.3232 (0.2198,0.3791) | ||
| (1.0,0.5,0.5) | 40 | 40 | 1.0778 (0.3812,0.2744) | 1.0787 (0.1936,0.1471) | 1.0251 (0.1533,0.1191) |
| 30 | 1.0040 (0.6560,0.4307) | 0.7944 (0.2908,0.2449) | 0.8300 (0.2613,0.2162) | ||
| 20 | 1.2427 (1.8647,0.7604) | 0.7024 (0.4310,0.3690) | 0.6739 (0.4149,0.3573) | ||
| 60 | 60 | 1.0423 (0.2756,0.2103) | 1.0358 (0.1384,0.1074) | 1.0081 (0.1224,0.0963) | |
| 45 | 0.9583 (0.4883,0.3602) | 0.8395 (0.2659,0.2175) | 0.8252 (0.2587,0.2117) | ||
| 30 | 0.9968 (0.7368,0.5038) | 0.6790 (0.4301,0.3682) | 0.6804 (0.4167,0.3547) | ||
| 80 | 80 | 1.0356 (0.2400,0.1773) | 1.0170 (0.1138,0.0890) | 1.0178 (0.1098,0.0864) | |
| 60 | 0.9068 (0.3824,0.2994) | 0.8297 (0.2577,0.2099) | 0.8247 (0.2544,0.2073) | ||
| 40 | 0.9375 (0.5979,0.4590) | 0.6725 (0.4279,0.3646) | 0.6710 (0.4196,0.3572) | ||
| n | m | MLE | MCMC | ||
|---|---|---|---|---|---|
| Prior (1) | Prior (2) | ||||
| (0.5,0.1,0.1) | 40 | 40 | 0.1032 (0.0576,0.4315) | 0.0918 (0.0167,0.1389) | 0.0894 (0.0127,0.1077) |
| 30 | 0.1236 (0.0869,0.6335) | 0.0951 (0.0171,0.1404) | 0.1050 (0.0138,0.1178) | ||
| 20 | 0.1651 (0.1664,1.1435) | 0.0922 (0.0267,0.2333) | 0.1143 (0.0230,0.1884) | ||
| 60 | 60 | 0.1032 (0.0463,0.3600) | 0.0908 (0.0094,0.0918) | 0.0935 (0.0069,0.0653) | |
| 45 | 0.1205 (0.0759,0.5598) | 0.0997 (0.0116,0.0927) | 0.1034 (0.0106,0.0772) | ||
| 30 | 0.1576 (0.1349,0.9860) | 0.0899 (0.0185,0.1541) | 0.1070 (0.0131,0.1052) | ||
| 80 | 80 | 0.0999 (0.0377,0.2949) | 0.1018 (0.0034,0.0248) | 0.0997 (0.0054,0.0465) | |
| 60 | 0.1173 (0.0645,0.5038) | 0.1002 (0.0073,0.0582) | 0.1026 (0.0060,0.0510) | ||
| 40 | 0.1573 (0.1213,0.9165) | 0.1064 (0.0146,0.1099) | 0.1096 (0.0111,0.0964) | ||
| (1.0,0.5,0.5) | 40 | 40 | 0.5255 (0.2675,0.4154) | 0.5263 (0.0329,0.0532) | 0.4938(0.0204,0.0365) |
| 30 | 0.6253 (0.4660,0.6616) | 0.4578 (0.0459,0.0843) | 0.5156 (0.0234,0.0350) | ||
| 20 | 0.9423 (0.9660,1.2917) | 0.5326 (0.0518,0.0764) | 0.5254 (0.0333,0.0551) | ||
| 60 | 60 | 0.5158 (0.2204,0.3440) | 0.5124 (0.0136,0.0248) | 0.4939 (0.0109,0.0161) | |
| 45 | 0.6043 (0.3689,0.5509) | 0.5225 (0.0323,0.0517) | 0.5193 (0.0223,0.0402) | ||
| 30 | 0.8500 (0.7219,1.0446) | 0.5405 (0.0454,0.0810) | 0.5331 (0.0352,0.0663) | ||
| 80 | 80 | 0.5118 (0.1879,0.2942) | 0.5059 (0.0063,0.0119) | 0.5047 (0.0061,0.0109) | |
| 60 | 0.5871 (0.3089,0.4833) | 0.5219 (0.0241,0.0438) | 0.5180 (0.0197,0.0360) | ||
| 40 | 0.8212 (0.6443,0.9580) | 0.5429 (0.0451,0.0857) | 0.5406 (0.0436,0.0812) | ||
| n | m | MLE | MCMC | ||
|---|---|---|---|---|---|
| Prior (1) | Prior (2) | ||||
| (0.5,0.1,0.1) | 40 | 40 | 0.1260 (0.0830,0.6041) | 0.1195 (0.0260,0.2072) | 0.0920 (0.0098,0.0809) |
| 30 | 0.1275 (0.1167,0.7961) | 0.1358 (0.0417,0.3606) | 0.0940 (0.0111,0.0903) | ||
| 20 | 0.1464 (0.2073,1.3049) | 0.0845 (0.0480,0.4256) | 0.1240 (0.0284,0.2452) | ||
| 60 | 60 | 0.1164 (0.0616,0.4733) | 0.0942 (0.0064,0.0583) | 0.1013 (0.0026,0.0220) | |
| 45 | 0.1154 (0.0866,0.6312) | 0.1070 (0.0142,0.1008) | 0.1081 (0.0118,0.0953) | ||
| 30 | 0.1224 (0.1576,1.0183) | 0.1009 (0.0217,0.1749) | 0.0915 (0.0189,0.1452) | ||
| 80 | 80 | 0.1142 (0.0512,0.3945) | 0.1045 (0.0053,0.0454) | 0.1007 (0.0023,0.0192) | |
| 60 | 0.1124 (0.0826,0.5780) | 0.1067 (0.0089,0.0767) | 0.0951 (0.0073,0.0567) | ||
| 40 | 0.1047 (0.1233,0.8588) | 0.0908 (0.0195,0.1624) | 0.1073 (0.0117,0.0864) | ||
| (1.0,0.5,0.5) | 40 | 40 | 0.5831 (0.3268,0.4871) | 0.5626 (0.0647,0.1253) | 0.5420 (0.0438,0.0840) |
| 30 | 0.6044 (0.5502,0.7128) | 0.5832 (0.0863,0.1663) | 0.4607 (0.0577,0.0917) | ||
| 20 | 0.5877 (0.8856,1.1044) | 0.5958 (0.1005,0.1916) | 0.4621 (0.0628,0.1061) | ||
| 60 | 60 | 0.5564 (0.2585,0.3954) | 0.5169 (0.0176,0.0338) | 0.5057 (0.0117,0.0170) | |
| 45 | 0.5493 (0.3978,0.5602) | 0.5270 (0.0405,0.0649) | 0.4786 (0.0273,0.0466) | ||
| 30 | 0.5250 (0.6820,0.8798) | 0.5609 (0.0642,0.1217) | 0.5461 (0.0494,0.0923) | ||
| 80 | 80 | 0.5427 (0.2162,0.3345) | 0.4927 (0.0082,0.0147) | 0.5049 (0.0059,0.0100) | |
| 60 | 0.5247 (0.3322,0.4831) | 0.5110 (0.0141,0.0237) | 0.4892 (0.0131,0.0221) | ||
| 40 | 0.4866 (0.5702,0.7752) | 0.5479 (0.0517,0.0959) | 0.5171 (0.0192,0.0343) | ||
| ACI | BCI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior (1) | Prior (2) | Prior (1) | Prior (2) | Prior (1) | Prior (2) | ||||||
| (0.5,0.1,0.1) | 40 | 40 | 0.3485 | 0.1039 | 0.0039 | 0.3352 | 0.2808 | 0.0594 | 0.0215 | 0.0639 | 0.0173 |
| 30 | 0.3807 | 0.1115 | 0.0031 | 0.4424 | 0.4216 | 0.0625 | 0.0467 | 0.0783 | 0.0333 | ||
| 20 | 0.4208 | 0.1444 | 0.0118 | 0.4760 | 0.5772 | 0.0774 | 0.0696 | 0.1437 | 0.0581 | ||
| 60 | 60 | 0.2646 | 0.0577 | 0.0019 | 0.2387 | 0.2347 | 0.0092 | 0.0077 | 0.0082 | 0.0088 | |
| 45 | 0.3091 | 0.1168 | 0.0033 | 0.3912 | 0.3890 | 0.0463 | 0.0400 | 0.0475 | 0.0321 | ||
| 30 | 0.3393 | 0.1537 | 0.0053 | 0.4458 | 0.4907 | 0.0632 | 0.0452 | 0.0828 | 0.0695 | ||
| 80 | 80 | 0.2213 | 0.0294 | 0.0008 | 0.2269 | 0.2228 | 0.0117 | 0.0174 | 0.0103 | 0.0087 | |
| 60 | 0.2572 | 0.0918 | 0.0023 | 0.3736 | 0.3674 | 0.0284 | 0.0201 | 0.0229 | 0.0201 | ||
| 40 | 0.2689 | 0.1219 | 0.0054 | 0.4756 | 0.4753 | 0.0526 | 0.0207 | 0.0676 | 0.0309 | ||
| 40 | 40 | 0.6913 | 0.3121 | 0.0153 | 0.6838 | 0.5868 | 0.0766 | 0.0673 | 0.0639 | 0.0506 | |
| 30 | 0.9376 | 0.5906 | 0.0391 | 0.8035 | 0.7754 | 0.0657 | 0.0670 | 0.0931 | 0.1271 | ||
| 20 | 1.5049 | 0.7474 | 0.0476 | 1.1633 | 0.9696 | 0.1527 | 0.0868 | 0.1097 | 0.1546 | ||
| 60 | 60 | 0.5241 | 0.1494 | 0.0051 | 0.5250 | 0.4800 | 0.0202 | 0.0296 | 0.0177 | 0.0361 | |
| 45 | 0.7699 | 0.5038 | 0.0213 | 0.8334 | 0.7452 | 0.0887 | 0.0457 | 0.0818 | 0.0631 | ||
| 30 | 0.8646 | 0.5170 | 0.0182 | 1.0647 | 0.9860 | 0.0740 | 0.0481 | 0.0791 | 0.0753 | ||
| 80 | 80 | 0.4425 | 0.1082 | 0.0041 | 0.4426 | 0.4213 | 0.0089 | 0.0148 | 0.0114 | 0.0106 | |
| 60 | 0.5357 | 0.3158 | 0.0094 | 0.7461 | 0.7131 | 0.0371 | 0.0248 | 0.0292 | 0.0243 | ||
| 40 | 0.7310 | 0.4141 | 0.0098 | 1.0136 | 0.9521 | 0.0512 | 0.0514 | 0.0608 | 0.0342 | ||
| Molel | |
|---|---|
| IE | |
| IW | |
| GIE | ) |
| IGa | |
| GIW | |
| EIW | |
| GIHL | |
| IK | |
| INH | |
| APIW |
| Measure or Criterion (C) | Abbreviation |
|---|---|
| negative log-likelihood | NLC |
| Akaike information | AIC |
| consistent Akaike information | CAIC |
| Bayesian information | BIC |
| Hannan-Quinn information | HQIC |
| Kolmogorov-Smirnov | K-S |
| Anderson-Darling | A-D |
| Cramér von Mises | CvM |
| K-S p-value | p-value |
| Model | Estimates (SEs) | Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NCL | AIC | CAIC | BIC | HQIC | K-S (p-Value) | A-D | CvM | ||||
| EIGo | 5.8897 (3.3256) | 418.743 (151.19) | 70.375 (25.031) | 155.330 | 316.659 | 317.802 | 320.316 | 317.674 | 0.114 (0.901) | 0.4141 | 0.0696 |
| GIW | 1.0110 (0.1412) | 6.8390 (92.567) | 12.370 (169.25) | 158.579 | 323.158 | 324.301 | 326.815 | 324.172 | 0.211 (0.215) | 1.5866 | 0.2803 |
| APIW | 39.651 (76.857) | 1.3072 (0.1886) | 115.74 (104.40) | 156.569 | 319.137 | 320.280 | 322.794 | 320.151 | 0.189 (0.336) | 1.2512 | 0.2226 |
| IE | - | - | 82.841 (16.568) | 158.582 | 319.841 | 319.338 | 320.383 | 319.205 | 0.207 (0.234) | 1.5774 | 0.2787 |
| IK | 1.0282 (0.1472) | 94.040 (57.964) | - | 158.484 | 320.967 | 321.513 | 323.405 | 321.643 | 0.213 (0.208) | 1.5734 | 0.2780 |
| IW | - | 1.0118 (0.1414) | 86.718 (50.775) | 158.579 | 321.158 | 321.703 | 323.596 | 321.834 | 0.211 (0.215) | 1.5873 | 0.2804 |
| IGa | - | 1.2166 (0.3081) | 100.65 (31.349) | 158.294 | 320.588 | 321.133 | 323.025 | 321.264 | 0.241 (0.110) | 1.5801 | 0.2791 |
| IGo | - | 101.08 (26.705) | 14.535 (14.283) | 158.001 | 320.003 | 320.548 | 322.440 | 320.679 | 0.222 (0.169) | 1.2406 | 0.2203 |
| INH | - | 0.7552 (0.2303) | 134.21 (76.920) | 158.208 | 320.416 | 320.962 | 322.854 | 321.093 | 0.218 (0.186) | 1.3574 | 0.2400 |
| GIE | - | 1.3462 (0.3991) | 100.68 (26.199) | 158.090 | 320.181 | 320.726 | 322.618 | 320.857 | 0.249 (0.091) | 1.5393 | 0.2720 |
| EIW | - | 86.324 (50.423) | 1.0108 (0.1411) | 158.579 | 321.158 | 321.703 | 323.596 | 321.834 | 0.211 (0.216) | 1.5864 | 0.2802 |
| GIHL | - | 0.9758 (0.2592) | 0.0089 (0.0020) | 160.087 | 324.175 | 324.720 | 326.612 | 324.851 | 0.263 (0.062) | 1.8631 | 0.3307 |
| Model | Estimates (SEs) | Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NCL | AIC | CAIC | BIC | HQIC | K-S (p-Value) | A-D | CvM | ||||
| EIGo | 3.5359 (1.4251) | 2.3986 (0.7152) | 0.3749 (0.1605) | 40.768 | 87.536 | 88.459 | 91.739 | 88.880 | 0.089 (0.971) | 0.1762 | 0.0286 |
| GIW | 1.0730 (0.1314) | 0.0761 (0.8851) | 11.920 (148.78) | 46.376 | 98.751 | 99.674 | 102.95 | 100.10 | 0.134(0.656) | 1.0815 | 0.1634 |
| APIW | 99.979 (157.11) | 1.4079 (0.1745) | 0.1922 (0.0751) | 43.188 | 92.376 | 93.300 | 96.580 | 93.721 | 0.113 (0.836) | 0.6445 | 0.0977 |
| IE | - | - | 0.7932 (0.1448) | 46.533 | 95.066 | 95.209 | 96.467 | 95.514 | 0.160 (0.423) | 1.0040 | 0.1509 |
| IK | 2.4609 (0.4214) | 4.1716 (1.2783) | - | 41.238 | 86.476 | 86.921 | 89.279 | 87.373 | 0.111 (0.852) | 0.3324 | 0.0495 |
| IW | - | 1.0730 (0.1314) | 0.7518 (0.1570) | 46.376 | 96.751 | 97.196 | 99.554 | 97.648 | 0.134 (0.656) | 1.0814 | 0.1634 |
| IGa | - | 1.4211 (0.3327) | 1.1272 (0.3153) | 45.507 | 95.015 | 95.459 | 97.817 | 95.911 | 0.158 (0.445) | 1.0080 | 0.1516 |
| IGo | - | 0.9290 (0.2107) | 0.1091 (0.1068) | 45.920 | 95.839 | 96.284 | 98.642 | 96.737 | 0.192 (0.216) | 0.6357 | 0.0956 |
| INH | - | 0.8517 (0.2346) | 1.0344 (0.5127) | 46.370 | 95.740 | 97.185 | 99.543 | 97.637 | 0.179 (0.295) | 0.8525 | 0.1270 |
| GIE | - | 1.6681 (0.4724) | 1.0975 (0.2480) | 44.966 | 93.931 | 94.376 | 96.734 | 94.828 | 0.163 (0.401) | 0.9099 | 0.1361 |
| EIW | - | 0.7518 (0.1570) | 1.0730 (0.1314) | 46.376 | 96.751 | 97.196 | 99.554 | 97.648 | 0.134 (0.656) | 1.0814 | 0.1634 |
| GIHL | - | 1.2154 (0.3164) | 0.7959 (0.1626) | 46.828 | 97.657 | 98.101 | 100.46 | 98.553 | 0.179 (0.291) | 1.1995 | 0.1855 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elshahhat, A.; Aljohani, H.M.; Afify, A.Z. Bayesian and Classical Inference under Type-II Censored Samples of the Extended Inverse Gompertz Distribution with Engineering Applications. Entropy 2021, 23, 1578. https://doi.org/10.3390/e23121578
Elshahhat A, Aljohani HM, Afify AZ. Bayesian and Classical Inference under Type-II Censored Samples of the Extended Inverse Gompertz Distribution with Engineering Applications. Entropy. 2021; 23(12):1578. https://doi.org/10.3390/e23121578
Chicago/Turabian StyleElshahhat, Ahmed, Hassan M. Aljohani, and Ahmed Z. Afify. 2021. "Bayesian and Classical Inference under Type-II Censored Samples of the Extended Inverse Gompertz Distribution with Engineering Applications" Entropy 23, no. 12: 1578. https://doi.org/10.3390/e23121578
APA StyleElshahhat, A., Aljohani, H. M., & Afify, A. Z. (2021). Bayesian and Classical Inference under Type-II Censored Samples of the Extended Inverse Gompertz Distribution with Engineering Applications. Entropy, 23(12), 1578. https://doi.org/10.3390/e23121578








