Blind and Secured Adaptive Digital Image Watermarking Approach for High Imperceptibility and Robustness
Abstract
:1. Introduction
2. Brief Overview
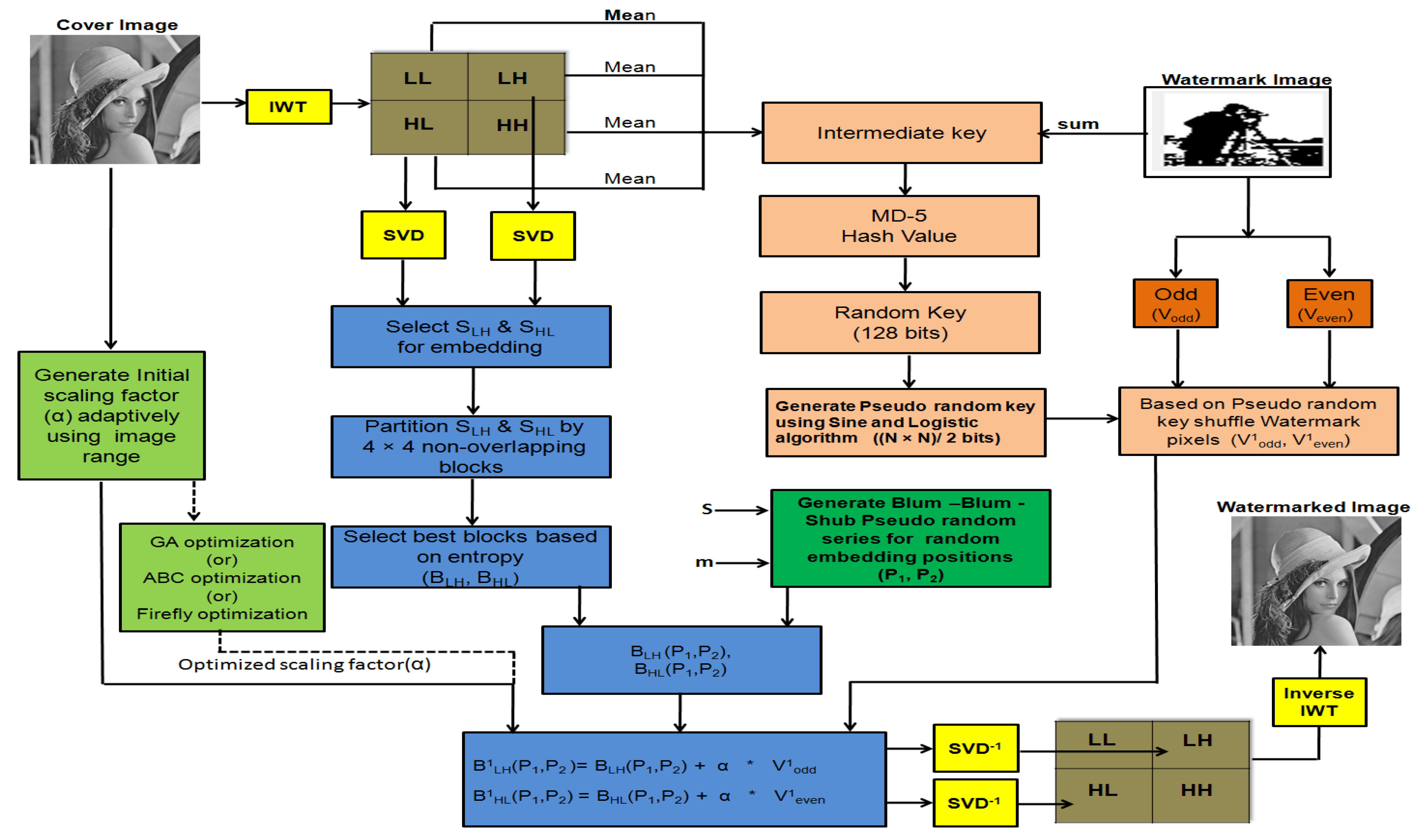
- High Watermark Security: The proposed scheme ensures twofold watermark security by encrypting the watermark and then embedding it in randomly selected positions in transformed cover image blocks. The watermark is partitioned into odd and even position pixel vectors. These vectors are encrypted by using pseudo random keys generated adaptively from the mean of IWT transformed sub-bands (LL, LH, HL, HH) of the cover image and the sum of the watermark image and key generation algorithm. The encrypted watermark is embedded in randomly selected pixel positions within the adaptively selected block using a Blum–Blum–Shum pseudo random generator.
- High Imperceptibility: In the proposed scheme, an Initial scaling factor (ISF) is adaptively generated from the cover image using a fuzzy based texture range filter to ensure higher imperceptibility. In addition, adaptive selection of low entropy blocks for embedding, increasing the imperceptibility.
- High Robustness: A hybrid IWT–SVD transformation is used in the proposed scheme to ensure high robustness. Adaptive ISF generation and block selection for embedding also improve the robustness
- Scaling Factor Optimization: To improve imperceptibility, robustness and balancing the trade-off in watermarking characteristics, optimization of ISF is proposed, if the computational cost is not the major concern in the application. NIO algorithms such as GA, ABC, and FO can be used for optimization.
3. Proposed Work
3.1. Watermark Embedding and Extraction
- Select two prime numbers ‘a’ and ‘b’ and both are congruent to a(mod b).
- Calculate the product of ‘a’ and ‘b’, say m. i.e., .
- Find integer as a co-prime for m, which is taken as the seed value ().
| Algorithm 1 Watermark embedding. |
|
| Algorithm 2 Watermark extraction. |
|
3.2. Watermark Encryption and Decryption
| Algorithm 3 Watermark encryption. |
|
| Algorithm 4 Pseudo random key generation from Random key. |
|
3.3. Initial Scaling Factor Generation and Optimization
| Algorithm 5 Initial Scaling Factor generation. |
|
4. Experimental Results and Discussion
4.1. Imperceptibility Test
4.2. Robustness
4.2.1. Adaptive ISF
4.2.2. Optimized ISF
4.3. Security Test
4.4. Computational Time
4.5. Comparative Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, C.; Singh, A.K.; Kumar, P. A recent survey on image watermarking techniques and its application in e-governance. Multimed. Tools Appl. 2018, 77, 3597–3622. [Google Scholar] [CrossRef]
- Ray, A.; Roy, S. Recent trends in image watermarking techniques for copyright protection: A survey. Int. J. Multimed. Inf. Retr. 2020, 9, 249–270. [Google Scholar] [CrossRef]
- Singh, L.; Singh, A.K.; Singh, P.K. Secure data hiding techniques: A survey. Multimed. Tools Appl. 2020, 79, 15901–15921. [Google Scholar] [CrossRef]
- Agarwal, N.; Singh, A.K.; Singh, P.K. Survey of robust and imperceptible watermarking. Multimed. Tools Appl. 2019, 78, 8603–8633. [Google Scholar] [CrossRef]
- Maheshkar, S. Region-based hybrid medical image watermarking for secure telemedicine applications. Multimed. Tools Appl. 2017, 76, 3617–3647. [Google Scholar]
- Zhang, H.; Wang, C.; Zhou, X. A robust image watermarking scheme based on SVD in the spatial domain. Future Internet 2017, 9, 45. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Pal, A.K. An indirect watermark hiding in discrete cosine transform–singular value decomposition domain for copyright protection. R. Soc. Open Sci. 2017, 4, 170326. [Google Scholar] [CrossRef] [Green Version]
- Rakhmawati, L.; Wirawan, W.; Suwadi, S. A recent survey of self-embedding fragile watermarking scheme for image authentication with recovery capability. EURASIP J. Image Video Process. 2019, 2019, 61. [Google Scholar] [CrossRef] [Green Version]
- Ramasamy, R.; Arumugam, V. Robust image watermarking using fractional Krawtchouk transform with optimization. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 7121–7132. [Google Scholar] [CrossRef]
- Salavi, R.R.; Math, M.M.; Kulkarni, U. A survey of various cryptographic techniques: From traditional cryptography to fully homomorphic encryption. In Innovations in Computer Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 295–305. [Google Scholar]
- Su, Q.; Chen, B. Robust color image watermarking technique in the spatial domain. Soft Comput. 2018, 22, 91–106. [Google Scholar] [CrossRef]
- Dhar, J.P.; Islam, M.S.; Ullah, M.A. A fuzzy logic based contrast and edge sensitive digital image watermarking technique. SN Appl. Sci. 2019, 1, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Arora, M.; Khurana, M. Secure image encryption technique based on jigsaw transform and chaotic scrambling using digital image watermarking. Opt. Quantum. Electron. 2020, 52, 1–30. [Google Scholar] [CrossRef]
- Gao, H.; Gao, T. Double verifiable image encryption based on chaos and reversible watermarking algorithm. Multimed. Tools Appl. 2019, 78, 7267–7288. [Google Scholar] [CrossRef]
- Mishra, A.; Agarwal, C.; Sharma, A.; Bedi, P. Optimized gray-scale image watermarking using DWT–SVD and Firefly Algorithm. Expert Syst. Appl. 2014, 41, 7858–7867. [Google Scholar] [CrossRef]
- Luo, A.W.; Gong, L.H.; Zhou, N.R.; Zou, W.P. Adaptive and blind watermarking scheme based on optimal SVD blocks selection. Multimed. Tools Appl. 2020, 79, 243–261. [Google Scholar] [CrossRef]
- Zheng, Z.; Saxena, N.; Mishra, K.; Sangaiah, A.K. Guided dynamic particle swarm optimization for optimizing digital image watermarking in industry applications. Future Gener. Comput. Syst. 2018, 88, 92–106. [Google Scholar] [CrossRef]
- Ansari, I.A.; Pant, M. Multipurpose image watermarking in the domain of DWT based on SVD and ABC. Pattern Recognit. Lett. 2017, 94, 228–236. [Google Scholar] [CrossRef]
- Hu, H.T.; Hsu, L.Y. Collective blind image watermarking in DWT-DCT domain with adaptive embedding strength governed by quality metrics. Multimed. Tools Appl. 2017, 76, 6575–6594. [Google Scholar] [CrossRef]
- Agarwal, C.; Mishra, A.; Sharma, A. A novel gray-scale image watermarking using hybrid Fuzzy-BPN architecture. Egypt. Informatics J. 2015, 16, 83–102. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, H.; Sharma, J.B. An adaptive color image watermarking using RDWT-SVD and artificial bee colony based quality metric strength factor optimization. Appl. Soft Comput. 2019, 84, 105696. [Google Scholar] [CrossRef]
- Makbol, N.M.; Khoo, B.E.; Rassem, T.H.; Loukhaoukha, K. A new reliable optimized image watermarking scheme based on the integer wavelet transform and singular value decomposition for copyright protection. Inf. Sci. 2017, 417, 381–400. [Google Scholar] [CrossRef]
- Zainol, Z.; Teh, J.S.; Alawida, M. A new chaotic image watermarking scheme based on SVD and IWT. IEEE Access 2020, 8, 43391–43406. [Google Scholar]
- Xiao, B.; Luo, J.; Bi, X.; Li, W.; Chen, B. Fractional discrete Tchebyshev moments and their applications in image encryption and watermarking. Inf. Sci. 2020, 516, 545–559. [Google Scholar] [CrossRef]
- Kumar, C.A.; Naik, B.R. A new encrypted image watermarking based on DTCWT and random pixel exchange. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; pp. 567–570. [Google Scholar]
- Vahedi, E.; Zoroofi, R.A.; Shiva, M. Toward a new wavelet-based watermarking approach for color images using bio-inspired optimization principles. Digit. Signal Process. 2012, 22, 153–162. [Google Scholar] [CrossRef]
- Sharma, V.; Mir, R.N. An enhanced time efficient technique for image watermarking using ant colony optimization and light gradient boosting algorithm. J. King Saud-Univ.-Comput. Inf. Sci. 2019. [Google Scholar] [CrossRef]
- Devi, K.J.; Singh, P. Secured Cross Layered Watermark Embedding For Digital Image Authentication Using IWT-SVD. In Proceedings of the 2020 IEEE 15th International Conference on Industrial and Information Systems (ICIIS), Rupnagar, India, 26–28 November 2020; pp. 269–273. [Google Scholar]
- Hua, G.; Xiang, Y.; Zhang, L.Y. Informed histogram-based watermarking. IEEE Signal Process. Lett. 2020, 27, 236–240. [Google Scholar] [CrossRef]
- Gao, X.; Deng, C.; Li, X.; Tao, D. Geometric distortion insensitive image watermarking in affine covariant regions. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2010, 40, 278–286. [Google Scholar] [CrossRef]
- Moeinaddini, E. Selecting optimal blocks for image watermarking using entropy and distinct discrete firefly algorithm. Soft Comput. 2019, 23, 9685–9699. [Google Scholar] [CrossRef]
- Singh, S.P.; Bhatnagar, G. A simplified watermarking algorithm based on lifting wavelet transform. Multimed. Tools Appl. 2019, 78, 20765–20786. [Google Scholar] [CrossRef]
- Ahmadi, M.; Norouzi, A.; Karimi, N.; Samavi, S.; Emami, A. ReDMark: Framework for residual diffusion watermarking based on deep networks. Expert Syst. Appl. 2020, 146, 113157. [Google Scholar] [CrossRef]
- Shah, T.; Jamal, S.S. An improved chaotic cryptosystem for image encryption and digital watermarking. Wirel. Pers. Commun. 2020, 110, 1429–1442. [Google Scholar]
- Liu, R.; Tan, T. An SVD-based watermarking scheme for protecting rightful ownership. IEEE Trans. Multimed. 2002, 4, 121–128. [Google Scholar]
- The USC-SIPI Image Database. Available online: https:/sipi.usc.edu/database/ (accessed on 27 May 2021).
- Uncompressed Colour Image Database (UCID). Available online: https://qualinet.github.io/databases/image/uncompressed_color_image_database_ucid/ (accessed on 27 May 2021).
















| Grayscale Image | MSE | PSNR (dB) | SSIM | NC | BER | Alpha |
|---|---|---|---|---|---|---|
| Lena | 0.4315 | 51.67 | 0.9853 | 1 | 0 | 1.03417 |
| Baboon | 0.4395 | 51.58 | 0.9982 | 1 | 0 | 3.93945 |
| Lighthouse | 0.3755 | 52.41 | 0.9530 | 1 | 0 | 0.59863 |
| Desert | 0.3663 | 52.50 | 0.9657 | 1 | 0 | 0.68652 |
| Grain | 0.4573 | 51.52 | 0.9867 | 1 | 0 | 2.93261 |
| MRI | 0.3009 | 53.31 | 0.9035 | 1 | 0 | 0.57421 |
| Avearage | 0.3951 | 52.16 | 0.9654 | 1 | 0 | |
| Color Image | MSE | PSNR | SSIM | NC | BER | Apha |
| Koala | 0.1538 | 56.31 | 0.9991 | 0.9991 | 0.0022 | 2.33984 |
| Penguins | 0.1319 | 56.90 | 0.9990 | 0.9992 | 0.0015 | 0.48535 |
| Tulips | 0.9919 | 60.85 | 1 | 0.0001 | 0.41992 | |
| Tiffany | 0.0865 | 58.76 | 0.9977 | 0.9901 | 0.0308 | 0.45898 |
| Splash | 0.1080 | 57.79 | 0.9976 | 0.9899 | 0.0229 | 1.07324 |
| Skin | 0.1336 | 56.75 | 0.9999 | 0.9992 | 0.0014 | 2.07812 |
| Average | 0.0112 | 57.89 | 0.9988 | 0.9949 | 0.0115 |
| Image | MSE | PSNR (dB) | SSIM | NC | BER | Alpha |
|---|---|---|---|---|---|---|
| Grass (1.1.01) | 0.4129 | 52.03 | 0.9999 | 1 | 0 | 6.7734 |
| Bark (1.1.02) | 0.4362 | 51.74 | 0.9995 | 1 | 0 | 7.7979 |
| Straw (1.1.03) | 0.4399 | 51.71 | 0.9996 | 1 | 0 | 9.7490 |
| Herringbone weave (1.1.04) | 0.3934 | 52.18 | 0.9998 | 1 | 0 | 13.9102 |
| Woolen (1.1.05) | 0.4215 | 51.95 | 0.9992 | 1 | 0 | 6.5332 |
| Pressed calf leather (1.1.06) | 0.4194 | 51.89 | 0.9998 | 1 | 0 | 11.9004 |
| Beach sand (1.1.07) | 0.4356 | 51.79 | 0.9993 | 1 | 0 | 6.9023 |
| Water (1.1.08) | 0.3476 | 52.64 | 0.9969 | 1 | 0 | 2.9189 |
| Wood grain (1.1.09) | 0.4101 | 52.02 | 0.9983 | 1 | 0 | 2.7051 |
| Raffia (1.1.10) | 0.4186 | 51.95 | 0.9994 | 1 | 0 | 7.6084 |
| Grass (1.2.03) | 0.4472 | 52.78 | 0.9962 | 1 | 0 | 2.3681 |
| Brick wall (1.2.12) | 0.4522 | 52.54 | 0.9998 | 1 | 0 | 1.9532 |
| Tile roof (1.4.05) | 0.4119 | 51.98 | 0.9755 | 1 | 0 | 3.1567 |
| Wood fence (1.4.06) | 0.3810 | 52.32 | 0.9964 | 1 | 0 | 2.4517 |
| Metal grates (1.4.07) | 0.3897 | 52.24 | 0.9977 | 1 | 0 | 3.8203 |
| .Female (4.1.01) | 0.3085 | 53.19 | 0.9774 | 1 | 0 | 1.3779 |
| Couple (4.1.02) | 0.3041 | 53.28 | 0.9360 | 1 | 0 | 0.6797 |
| Female (4.1.03) | 0.2070 | 54.98 | 0.9424 | 1 | 0 | 0.4785 |
| Female (4.1.04) | 0.2912 | 53.52 | 0.9772 | 1 | 0 | 0.7607 |
| . House (4.1.05) | 0.2895 | 53.56 | 0.9681 | 1 | 0 | 1.2666 |
| Tree (4.1.06) | 0.3627 | 52.57 | 0.9731 | 1 | 0 | 1.6543 |
| Jelly bean (4.1.07) | 0.0899 | 58.59 | 0.9935 | 1 | 0 | 0.0332 |
| Airplane (4.2.05) | 0.4051 | 52.08 | 0.9697 | 1 | 0 | 0.9648 |
| Sail boat (4.2.06) | 0.4668 | 51.42 | 0.9909 | 1 | 0 | 1.6055 |
| Peppers (4.2.07) | 0.4632 | 51.49 | 0.9896 | 1 | 0 | 1.4355 |
| Moon surface (5.1.09) | 0.3321 | 52.92 | 0.9924 | 1 | 0 | 2.0449 |
| Aerial (5.1.10) | 0.4218 | 51.85 | 0.9961 | 1 | 0 | 2.6289 |
| Airplane (5.1.11) | 0.2134 | 54.81 | 0.9485 | 1 | 0 | 0.5557 |
| Clock (5.1.12) | 0.2541 | 54.07 | 0.9451 | 1 | 0 | 0.4590 |
| Resolution chart (5.1.13) | 0.1065 | 57.85 | 0.6537 | 1 | 0 | 0.0010 |
| Chemical paint (5.1.14) | 0.4021 | 52.07 | 0.9940 | 1 | 0 | 2.4258 |
| Couple (5.2.08) | 0.4415 | 51.68 | 0.9917 | 1 | 0 | 1.3770 |
| Aerial (5.2.09) | 0.4521 | 51.57 | 0.9936 | 1 | 0 | 1.8740 |
| Stream and Bridge (5.2.10) | 0.5907 | 50.43 | 0.9973 | 1 | 0 | 3.5762 |
| Male (5.3.01) | 0.4408 | 51.70 | 0.9909 | 1 | 0 | 1.5879 |
| Airport (5.3.02) | 0.4611 | 51.47 | 0.9925 | 1 | 0 | 1.6172 |
| Truck (7.1.01) | 0.4501 | 51.60 | 0.9925 | 1 | 0 | 1.6709 |
| Airplane (7.1.02) | 0.3204 | 53.02 | 0.9725 | 1 | 0 | 0.4961 |
| Car (7.1.03) | 0.4444 | 51.63 | 0.9948 | 1 | 0 | 2.1592 |
| Car and APCs (7.1.04) | 0.4155 | 51.89 | 0.9943 | 1 | 0 | 2.3555 |
| Truck and APCs (7.1.06) | 0.4430 | 51.66 | 0.9969 | 1 | 0 | 3.6641 |
| Tank (7.1.07) | 0.4351 | 51.79 | 0.9976 | 1 | 0 | 3.7002 |
| APC (7.1.08) | 0.4641 | 51.50 | 0.9891 | 1 | 0 | 1.2744 |
| Tank (7.1.09) | 0.4369 | 51.75 | 0.9972 | 1 | 0 | 2.9941 |
| Tank and APCs (7.1.10) | 0.4183 | 51,89 | 0.9958 | 1 | 0 | 2.6553 |
| Airplane (7.2 01) | 0.4031 | 52.03 | 0.9767 | 1 | 0 | 0.8965 |
| Fishing boat | 0.4486 | 51.57 | 0.9930 | 1 | 0 | 3.8765 |
| Level step wedge | 0.3216 | 52.87 | 0.9973 | 1 | 0 | 2.3144 |
| House | 0.4143 | 51.94 | 0.9677 | 1 | 0 | 1.9874 |
| Pixel ruler | 0.0924 | 58.47 | 0.8453 | 1 | 0 | 1.7432 |
| Average | 0.3813 | 51.55 | 0.9767 | 1 | 0 |
| Grayscale Images | With GA | With ABC | With FO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | SSIM | Alpha | PSNR (dB) | SSIM | Alpha | PSNR (dB) | SSIM | Alpha | |
| Lena | 53.14 | 0.9894 | 9.18692 | 52.32 | 0.9871 | 4.2647 | 52.29 | 0.9869 | 4.47517 |
| Mandrill | 51.96 | 0.9984 | 8.84809 | 51.60 | 0.9983 | 4.2157 | 51.60 | 0.9983 | 4.04169 |
| Lighthouse | 53.44 | 0.9597 | 9.34731 | 52.92 | 0.9570 | 4.1358 | 52.79 | 0.9560 | 3.63865 |
| Desert | 53.34 | 0.9713 | 6.06826 | 53.09 | 0.9707 | 4.2014 | 53.04 | 0.9706 | 3.82451 |
| Grain | 51.52 | 0.9862 | 6.18985 | 51.54 | 0.9866 | 4.0224 | 51.57 | 0.9845 | 5.04537 |
| MRI | 54.27 | 0.9062 | 5.69925 | 54.07 | 0.9059 | 3.8877 | 53.88 | 0.9055 | 2.70833 |
| Average | 52.95 | 0.9685 | 52.59 | 0.9676 | 52.52 | 0.9669 | |||
| Color Images | PSNR | SSIM | Apha | PSNR | SSIM | Apha | PSNR | SSIM | Apha |
| Koala | 57.11 | 0.9993 | 9.62690 | 56.56 | 0.9991 | 4.7327 | 56.48 | 0.9991 | 4.1267 |
| Penguins | 57.66 | 0.9990 | 9.88692 | 57.21 | 0.9990 | 4.7606 | 57.17 | 0.9990 | 3.9985 |
| Tulips | 61.50 | 1 | 6.67544 | 61.37 | 1 | 5.1535 | 61.35 | 1 | 4.9423 |
| Tiffany | 57.46 | 0.9978 | 9.80044 | 59.22 | 0.9978 | 4.7247 | 59.32 | 0.9972 | 4.2167 |
| Splash | 58.14 | 0.9976 | 5.32084 | 58.12 | 0.9977 | 6.5745 | 58.03 | 0.9976 | 5.9291 |
| Skin | 58.68 | 0.9999 | 9.26637 | 57.81 | 0.9999 | 4.8773 | 57.60 | 0.9999 | |
| Average | 58.42 | 0.9989 | 58.38 | 0.9989 | 58.32 | 0.9988 | |||
| Greyscale Imagee | With GA | With ABC | With FO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NC | BER | Apha | NC | BER | Apha | NC | BER | Apha | |
| Lena | 1 | 0 | 9.18692 | 1 | 0 | 4.2647 | 1 | 0 | 4.47517 |
| Baboon | 1 | 0 | 8.84809 | 1 | 0.0004 | 4.2157 | 1 | 0 | 4.04169 |
| Lighthouse | 1 | 0 | 9.34731 | 1 | 0.0002 | 4.1358 | 1 | 0 | 3.63865 |
| Desert | 1 | 0 | 6.06826 | 1 | 0.0002 | 4.2014 | 1 | 0 | 3.82451 |
| Grain | 1 | 0 | 6.18985 | 1 | 0 | 4.0224 | 1 | 0 | 5.04537 |
| MRI | 1 | 0 | 5.69925 | 1 | 0 | 3.8877 | 1 | 0 | 2.70833 |
| Average | 1 | 0 | 1 | 0.0001 | 1 | 0 | |||
| Color Images | NC | BER | Apha | NC | BER | Apha | NC | BER | Apha |
| Koala | 0.9999 | 0 | 9.62690 | 0.9996 | 0.0004 | 4.7327 | 0.9996 | 0 | 4.1267 |
| Penguins | 1 | 0.0004 | 9.88692 | 0.9997 | 0.0004 | 4.7606 | 0.9996 | 0.0004 | 3.9985 |
| Tulips | 1 | 0.0002 | 6.67544 | 1 | 0 | 5.1535 | 1 | 0 | 4.9423 |
| Tiffany | 0.9997 | 0.0002 | 9.80044 | 0.9990 | 0.0004 | 4.7247 | 0.9993 | 0 | 4.2167 |
| Splash | 0.9995 | 0 | 5.32084 | 0.9997 | 0 | 6.5745 | 0.9990 | 0 | 5.9291 |
| Skin | 0.9999 | 0 | 9.26637 | 0.9996 | 0 | 4.8773 | 0.9996 | 0 | 4.5178 |
| Average | 0.9998 | 0.0001 | 0.9996 | 0.0002 | 0.9991 | 0 | |||
| Attacks | With ISF (Alpha = 1.0341) | With GA (Alpha = 9.18619) | With ABC (Alpha = 4.2647) | With FO (Alpha = 4.4752) | ||||
|---|---|---|---|---|---|---|---|---|
| NC | BER | NC | BER | NC | BER | NC | BER | |
| Original | 1 | 0.0004 | 1 | 0 | 1 | 0 | 1 | 0 |
| Salt and Pepper (0.002) | 0.6954 | 0.5710 | 0.8592 | 0.5610 | 0.7701 | 0.5706 | 0.6859 | 0.5708 |
| Gaussian Noise (0.0002) | 0.9472 | 0.5710 | 0.9671 | 0.5551 | 0.9601 | 0.5640 | 0.9538 | 0.5701 |
| Speckle Noise (0.0002) | 0.9426 | 0.5710 | 0.9676 | 05624 | 0.9602 | 0.5668 | 0.9539 | 0.5702 |
| Poisson Noise | 0.9460 | 0.5710 | 0.9679 | 0.5590 | 0.9599 | 0.5623 | 0.9556 | 0.5689 |
| Cropping (25 % ) | 0.9378 | 0.5102 | 0.9566 | 0.4956 | 0.9500 | 0.5083 | 0.9439 | 0.4934 |
| Rotate_ 45 (clockwise) | 0.9703 | 0.0332 | 0.9958 | 0.0012 | 0.9897 | 0.0146 | 0.9909 | 0.0104 |
| Rotate _ 10 (clockwise) | 0.9993 | 0.0031 | 0.9997 | 0.0004 | 0.9994 | 0.0007 | 0.9994 | 0.0004 |
| Translate (24.3, 10.1) | 0.9905 | 0.0078 | 0.9990 | 0.0007 | 0.9983 | 0.0012 | 0.9982 | 0.0012 |
| Resize (256) | 0.9410 | 0.0078 | 0.9725 | 0.0007 | 0.9594 | 0.0012 | 0.9542 | 0.0010 |
| Resize (320) | 0.9835 | 0.0400 | 0.9950 | 0.0048 | 0.9905 | 0.0266 | 0.9910 | 0.0263 |
| Jpeg Compression (60%) | 0.9880 | 0.0183 | 0.9989 | 0.0004 | 0.9961 | 0.0065 | 0.9957 | 0.0041 |
| Sharpening | 0.9973 | 0.1269 | 0.9991 | 0.1054 | 0.9987 | 0.1293 | 0.9990 | 0.1396 |
| Gaussian Filter (3 by 3) | 1 | 0.0004 | 1 | 0 | 1 | 0.0004 | 1 | 0 |
| Median Filter (3 by 3) | 0.9952 | 0.0017 | 0.9976 | 0.0007 | 0.9973 | 0.0004 | 0.9970 | 0.0003 |
| Average Filter (3 by 3) | 0.9608 | 0.3940 | 0.9853 | 0.4416 | 0.9764 | 0.4118 | 0.9725 | 0.3950 |
| Average Filter (5 by 5) | 0.8555 | 0.4206 | 0.9119 | 0.3798 | 0.9027 | 0.3999 | 0.9922 | 0.0009 |
| Weiner Filter (3 by 3) | 0.9745 | 0.0146 | 0.9986 | 0.0004 | 0.9966 | 0.0034 | 0.9783 | 0.0144 |
| Butter worth Filter (Threshold = 20, Grade = 1) | 0.9602 | 0.5710 | 0.9895 | 0.4523 | 0.9854 | 0.4610 | 0.9876 | 0.4598 |
| Gamma Correctoin (0.25) | 0.9983 | 0.0021 | 0.9993 | 0.0004 | 0.9990 | 0.0012 | 0.9992 | 0.0009 |
| Gamma Correction (0.3) | 0.9983 | 0.0021 | 0.9994 | 0.0008 | 0.9991 | 0.0008 | 0.9990 | 0.0012 |
| Shear (x = 1, y = 0.2) | 0.9972 | 0.0009 | 0.9983 | 0.0004 | 0.9981 | 0.0004 | 0.9980 | 0.0004 |
| Test Images (Binary) | Correlation of Original and Encrypted Images | Correlation of Original and Decrypted Images | ||||
|---|---|---|---|---|---|---|
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal | |
| Cameraman | 0.1185 | 0.1263 | 0.0721 | 1 | 1 | 1 |
| Trishool | 0.1238 | 0.1628 | 0.1828 | 1 | 1 | 1 |
| Koala | 0.1472 | 0.1577 | 0.0165 | 1 | 1 | 1 |
| Lena | 0.1294 | 0.1376 | 0.0938 | 1 | 1 | 1 |
| Penguins | 0.1435 | 0.1237 | 0.1171 | 1 | 1 | 1 |
| Original Images | Correlation between Two Encrypted Images | ||
|---|---|---|---|
| Horizontal | Vertical | Diagonal | |
| Cameraman | −0.0281 | −0.0173 | −0.0611 |
| Trishool | −0.0248 | −0.0167 | −0.0231 |
| Koala | −0.0173 | −0.0104 | 0.0057 |
| Lena | −0.0086 | 0.0303 | 0.0017 |
| Penguins | −0.0253 | −0.0778 | −0.0237 |
| Operations | Computational Cost |
|---|---|
| 1-level 2D IWT transform | |
| 1-level 2D inverse IWT transform | |
| SVD decomposition | |
| SVD re-composition | |
| ISF Optimization | O(MN) |
| Adaptive block selection | |
| Determination of adaptive embedding position using BBS |
| Grayscale Image | Embedding Time (s) | Extraction Time (s) | Color Image | Embedding Time (s) | Extraction Time (s) |
|---|---|---|---|---|---|
| Lena | 1.919406 | 1.056093 | Koala | 1.378239 | 0.987560 |
| Baboon | 1.465614 | 0.915152 | Penguins | 1.686724 | 0.977352 |
| Lighthouse | 1.553255 | 1.025732 | Tulips | 1.433371 | 0.831694 |
| Desert | 1.324148 | 0.985283 | Tiffany | 1.277285 | 0.900063 |
| Grain | 1.264661 | 0.973439 | Splash | 1.244865 | 0.907733 |
| MRI | 1.470474 | 0.715602 | Skin | 1.273823 | 0.616617 |
| Average | 1.526388 | 0.995216 | Average | 1.382384 | 0.870169 |
| Parameters | Ansari and Pant. [18] | Moeinnaddini. [31] | Singh and Bhatnagar. [32] | Sharma and Mir. [27] | Zainol et al. [23] | Proposed |
|---|---|---|---|---|---|---|
| Scheme | Non-blind | Blind | Blind | Blind | Blind | Blind |
| Embedding domain | DWT + SVD | Hadmard | LWT + d-sequence | DCT | IWT + SVD | IWT + SVD |
| Cover image size | 512 by 512 | 512 by 512 | 512 by 512 | 512 by 512 | 512 by 512 | 512 by 512 |
| Watermark size | 64 by 64 | 64 by 64 | 16 by 16 | 64 by 64 | 256 by 256 | 64 by 64 |
| Security | Yes | Yes | Yes | No | Yes | Yes |
| Encryption approach | Arnold | No | Arnold | No | Chaotic map | Pseudo random key |
| Optimization algorithm | ABC | DDFA | No | ACO | No | GA, ABC, FA |
| Handling FPE | No | Yes | Yes | Yes | Yes | Yes |
| Embedding position | Principal component | Coefficients adjustments | Sub bands | DC component | Principal component | Principal component |
| Embedding type | Static | Dynamic | Static | Dynamic | Static | Dynamic |
| Embedding rate | 0.015625 | 0.015625 | 0.00097 | 0.015625 | 0.25 | 0.015625 |
| ABC Proposed | ABC [28] | GA Proposed | GA [28] | |||||
|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Grayscale Image | ||||||||
| Lena | 52.32 | 0.9971 | 47.45 | 0.9964 | 53.14 | 0.9894 | 50.81 | 0.9825 |
| Baboon | 51.60 | 0.9983 | 50.86 | 0.9961 | 51.96 | 0.9984 | 51.02 | 0.9931 |
| Lighthouse | 52.92 | 0.9570 | 52.37 | 0.9534 | 53.44 | 0.9597 | 51.89 | 0.9532 |
| Desert | 53.09 | 0.9707 | 52.61 | 0.9682 | 53.34 | 0.9713 | 51.95 | 0.9647 |
| Grain | 51.54 | 0.9866 | 51.04 | 0.9836 | 51.52 | 0.9862 | 50.73 | 0.9806 |
| MRI | 54.07 | 0.9059 | 53.06 | 0.9026 | 54.27 | 0.9062 | 53.01 | 0.9029 |
| Color Images | ||||||||
| Koala | 56.56 | 0.9991 | 49.11 | 0.9925 | 57.11 | 0.9993 | 56.02 | 0.999 |
| Penguins | 57.21 | 0.999 | 51.51 | 0.9998 | 57.66 | 0.999 | 56.02 | 0.9982 |
| Tulips | 61.37 | 1 | 48.18 | 0.9997 | 61.50 | 1 | 59.98 | 0.9999 |
| Tiffany | 59.22 | 0.9978 | 58.09 | 0.9977 | 57.46 | 0.9978 | 58.04 | 0.9977 |
| Splash | 58.12 | 0.9977 | 56.08 | 0.9976 | 58.14 | 0.9976 | 56.04 | 0.9976 |
| Skin | 57.81 | 0.9999 | 56.83 | 0.9998 | 58.68 | 0.9999 | 55.83 | 0.9998 |
| ABC Proposed | ABC [28] | GA Proposed | GA [28] | |||||
|---|---|---|---|---|---|---|---|---|
| NC | BER | NC | BER | NC | BER | NC | BER | |
| Grayscale Image | ||||||||
| Lena | 1 | 0 | 1 | 0.0004 | 1 | 0 | 1 | 0 |
| Baboon | 1 | 0.0004 | 1 | 0.0004 | 1 | 0 | 1 | 0 |
| Lighthouse | 1 | 0.0002 | 1 | 0.0002 | 1 | 0 | 1 | 0 |
| Desert | 1 | 0.0002 | 1 | 0 | 1 | 0 | 1 | 0 |
| Grain | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| MRI | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Color Images | ||||||||
| Koala | 0.9996 | 0.0004 | 0.9991 | 0.0019 | 0.9999 | 0 | 0.9977 | 0.0019 |
| Penguins | 0.9997 | 0.0004 | 0.9980 | 0.0017 | 1 | 0.0004 | 0.9991 | 0.0008 |
| Tulips | 1 | 0 | 0.9981 | 0.0009 | 1 | 0.0002 | 0.9961 | 0.0042 |
| Tiffany | 0.9998 | 0.0004 | 0.9903 | 0.0096 | 0.9997 | 0.0002 | 0.991 | 0.0351 |
| Splash | 0.9997 | 0 | 0.9896 | 0.0094 | 0.9995 | 0 | 0.9903 | 0.0093 |
| Skin | 0.9996 | 0 | 0.9950 | 0.0032 | 0.9999 | 0 | 0.9963 | 0.0059 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, P.; Devi, K.J.; Thakkar, H.K.; Santamaría, J. Blind and Secured Adaptive Digital Image Watermarking Approach for High Imperceptibility and Robustness. Entropy 2021, 23, 1650. https://doi.org/10.3390/e23121650
Singh P, Devi KJ, Thakkar HK, Santamaría J. Blind and Secured Adaptive Digital Image Watermarking Approach for High Imperceptibility and Robustness. Entropy. 2021; 23(12):1650. https://doi.org/10.3390/e23121650
Chicago/Turabian StyleSingh, Priyanka, Kilari Jyothsna Devi, Hiren Kumar Thakkar, and José Santamaría. 2021. "Blind and Secured Adaptive Digital Image Watermarking Approach for High Imperceptibility and Robustness" Entropy 23, no. 12: 1650. https://doi.org/10.3390/e23121650
APA StyleSingh, P., Devi, K. J., Thakkar, H. K., & Santamaría, J. (2021). Blind and Secured Adaptive Digital Image Watermarking Approach for High Imperceptibility and Robustness. Entropy, 23(12), 1650. https://doi.org/10.3390/e23121650









