Modeling Predictability of Traffic Counts at Signalised Intersections Using Hurst Exponent
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Hurst Exponent
- I.
- A value of H in the range [0.5–1] is indicative of long-term positive autocorrelation in the time series. In such cases, a high value in the series will likely be followed by another high value, i.e., the future trend is more likely to follow an established trend. For example, a very high H value (say H = 0.9) means a higher level of determinism, i.e., good predictability (PI = 0.8),
- II.
- H values close to 0.5 indicate an entirely uncorrelated series. It means that the values in the time series are random and potentially indicating Brownian motion. The PI, in this case, gets closer to 0 because it becomes challenging to “precisely” predict the stochastic variations.
- III.
- H value of 0 to 0.5 suggests the long-term fluctuation between high and low values in adjacent pairs of observations in the time series. A low H value (say H = 0.1) indicates a strong determinism. It is because a single high value will likely be succeeded by a low value or vice versa. Small magnitude H values in flow can be observed on downstream links at signalised intersections, mainly when the measurement interval is smaller than the cycle time of the signal. Due to strong determinism, the PI of the time series is high, even though H is low (PI = 0.8). Therefore, the PI for a time series is the same if the value of H is either 0.9 or 0.1. Furthermore, the PI increases when H approaches either 1 or 0 and decreases when it approaches 0.5.
3.2. Random-Effects Model
- = the dependent variable, where i = entity and t = time;
- α = the intercept term;
- = value of the independent variable for group i at time t;
- = coefficient of independent variables;
- = within entity error term, and
- = between entity error term.
4. Study Area and Data Collection
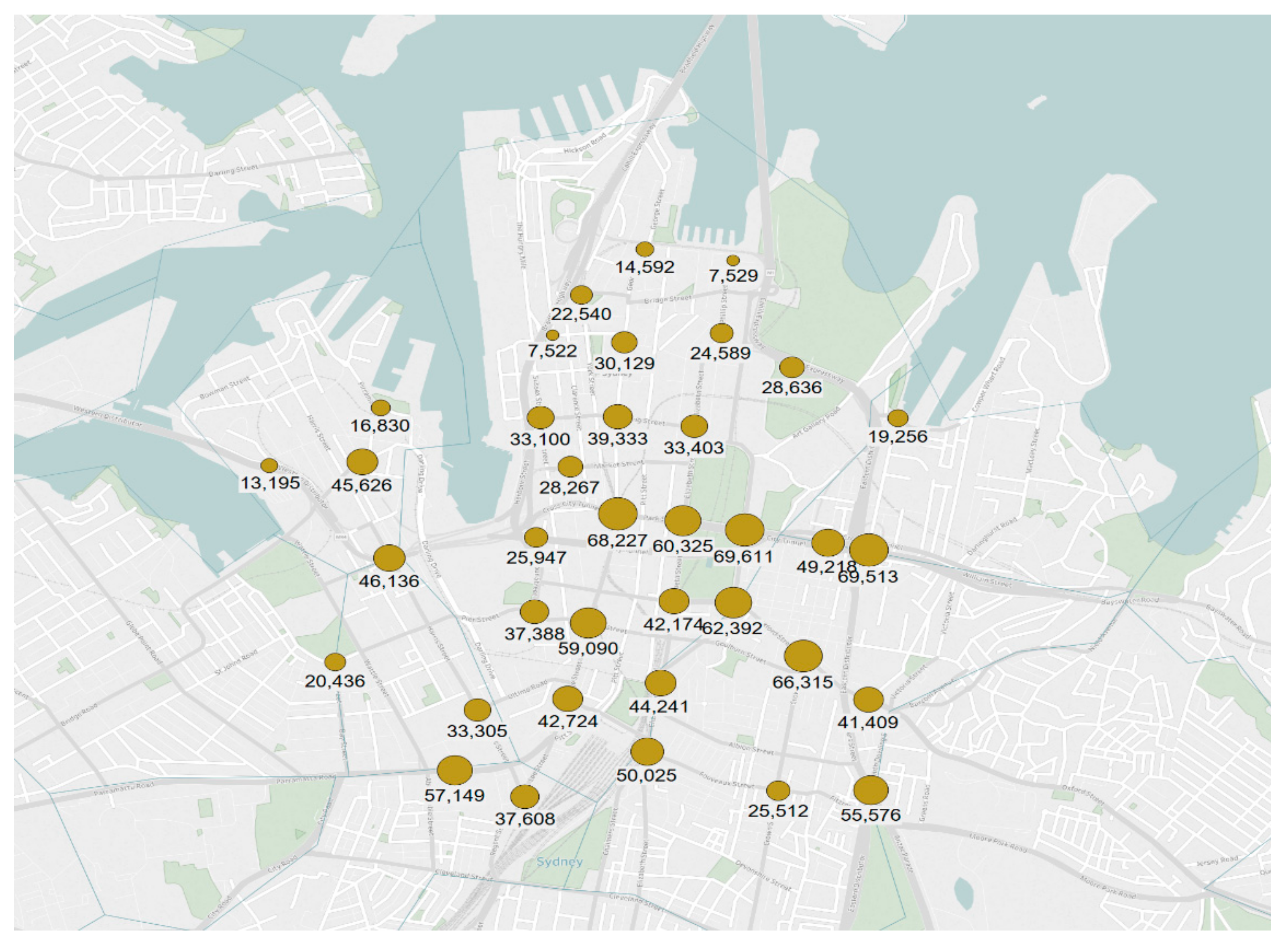
4.1. Study Area
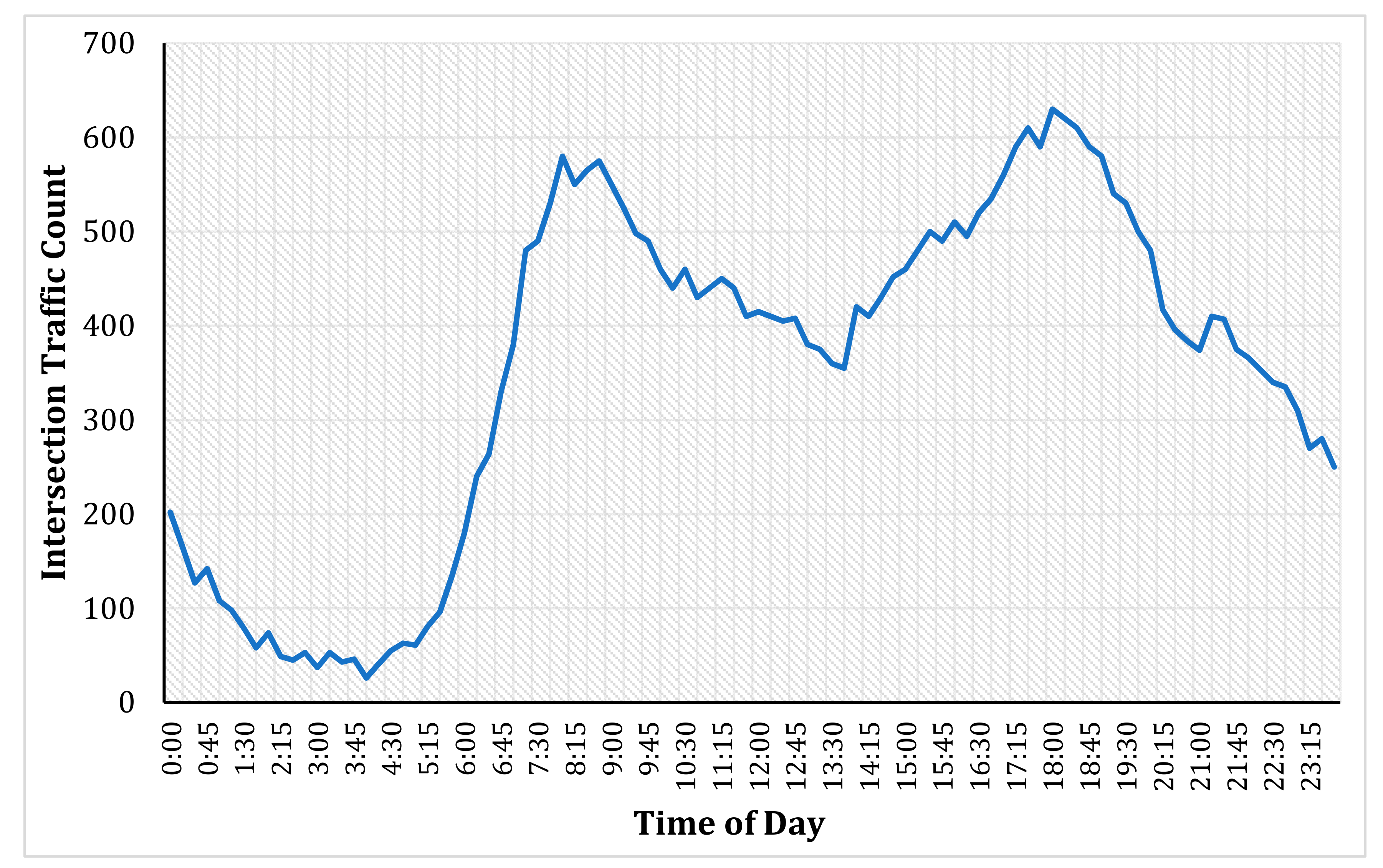
4.2. Data
5. Data Analysis
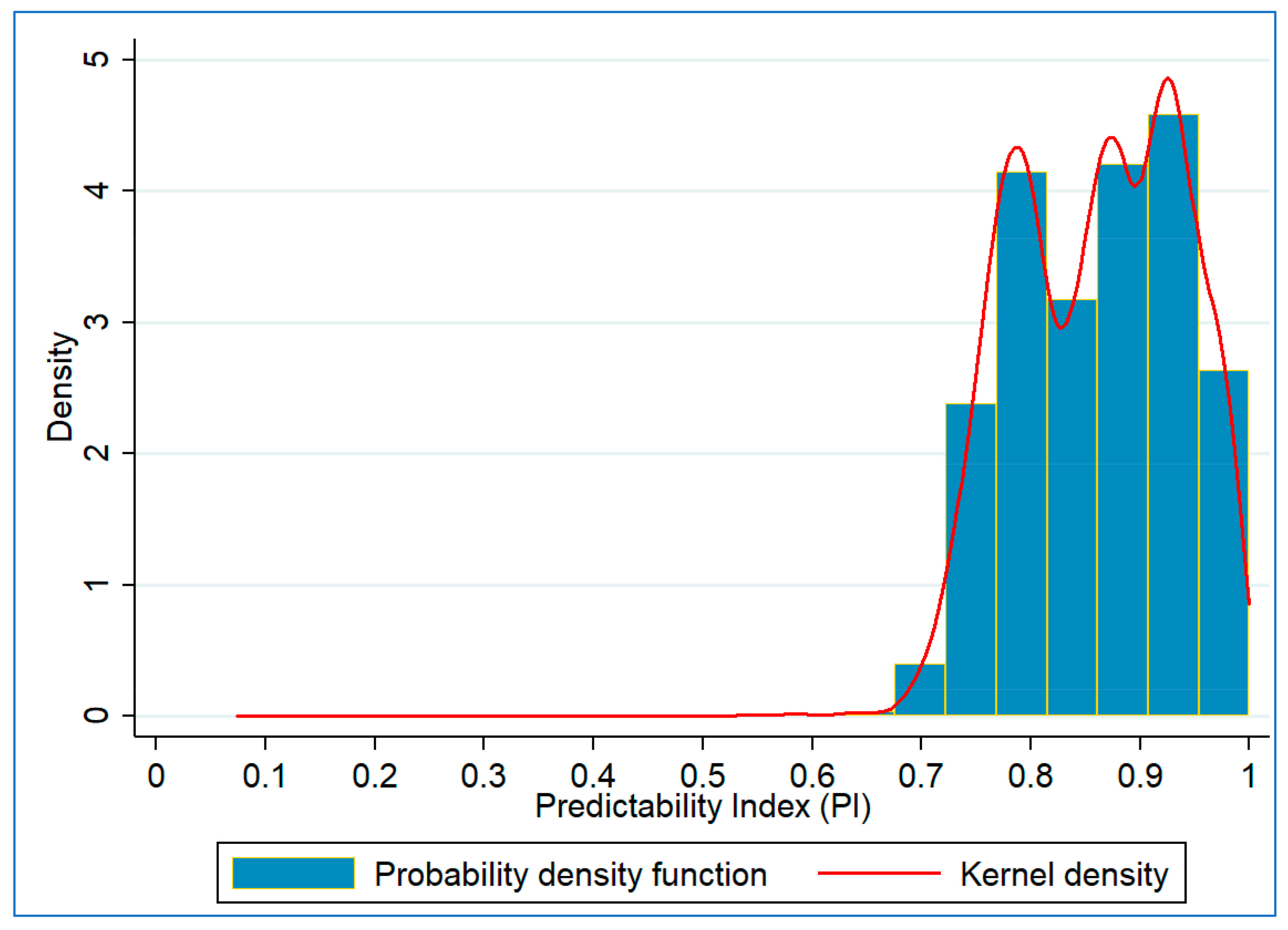
5.1. Preliminary Analysis
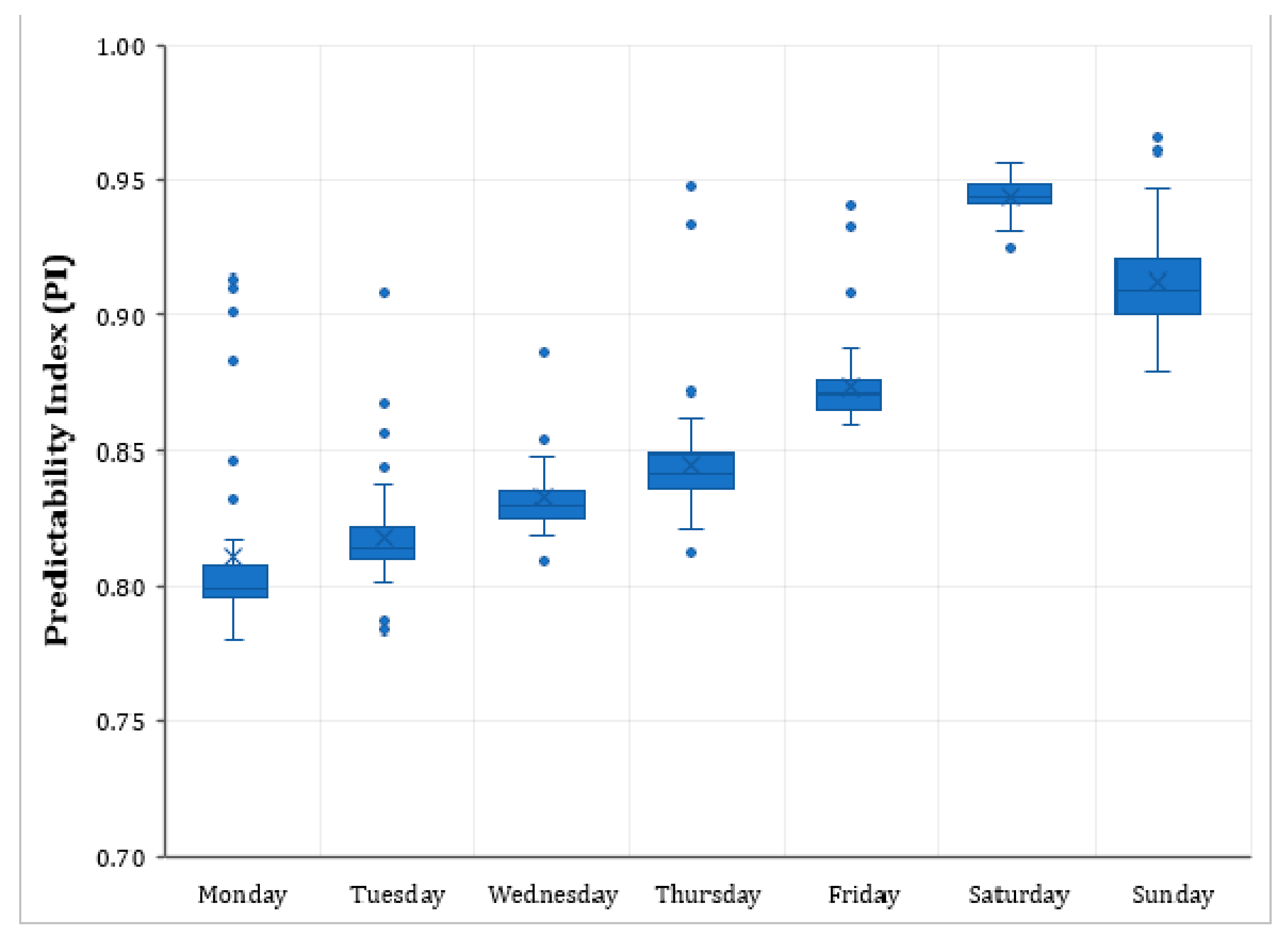
5.2. Model Results
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- FHWA Highway Statistics 2010; US Department of Transportation, Federal Highway Administration (FHWA): Washington, DC, USA, 2012.
- Rakha, H.; Van Aerde, M. Statistical Analysis of Day-to-Day Variations in Real-Time Traffic Flow Data. Transp. Res. Rec. 1995, 1510, 26–34. [Google Scholar]
- van Zuylen, H.; van Geenhuizen, M.; Nijkamp, P. (Un)Predictability in Traffic and Transport Decision Making. Transp. Res. Rec. J. Transp. Res. Board 1999, 1685, 21–29. [Google Scholar] [CrossRef]
- Turkay, C. Visualizing Time Series Predictability. In Proceedings of the IEEE VIS 2014 Workshop on Visualization for Predictive Analytics, Paris, France, 9 November 2014. [Google Scholar]
- Garland, J.; James, R.; Bradley, E. Model-Free Quantification of Time-Series Predictability. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 052910. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Yeh, A.G.O.; Zhuang, Y. Prediction Time Horizon and Effectiveness of Real-Time Data on Short-Term Traffic Predictability. In Proceedings of the 2007 IEEE Intelligent Transportation Systems Conference, Seattle, WA, USA, 30 September–3 October 2007; pp. 962–967. [Google Scholar]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.-L. Limits of Predictability in Human Mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef]
- Lu, X.; Bengtsson, L.; Holme, P. Predictability of Population Displacement After the 2010 Haiti Earthquake. PNAS 2012, 109, 11576–11581. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Wetter, E.; Bharti, N.; Tatem, A.J.; Bengtsson, L. Approaching the Limit of Predictability in Human Mobility. Sci. Rep. 2013, 3, 2923. [Google Scholar] [CrossRef]
- Lin, M.; Hsu, W.-J.; Lee, Z.Q. Predictability of Individuals’ Mobility with High-Resolution Positioning Data. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; ACM: Pittsburgh, PA, USA, 2012; pp. 381–390. [Google Scholar]
- Li, Y.; Jin, D.; Hui, P.; Wang, Z.; Chen, S. Limits of Predictability for Large-Scale Urban Vehicular Mobility. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2671–2682. [Google Scholar] [CrossRef]
- Wang, J.; Mao, Y.; Li, J.; Xiong, Z.; Wang, W.-X. Predictability of Road Traffic and Congestion in Urban Areas. PLoS ONE 2015, 10, e0121825. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Xu, X.; Hu, Y.; Li, X. An Entropy-Based Approach for Evaluating Travel Time Predictability Based on Vehicle Trajectory Data. Entropy 2017, 19, 165. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Q.; Sadek, A. Short-Term Forecasting of Traffic Volume: Evaluating Models Based on Multiple Data Sets and Data Diagnosis Measures. Transp. Res. Rec. J. Transp. Res. Board 2013, 2392, 40–47. [Google Scholar] [CrossRef]
- Valle, M.A.V.; García, G.M.; Cohen, I.S.; Klaudia-Oleschko, L.; Ruiz-Corral, J.A.; Korvin, G. Spatial Variability of the Hurst Exponent for the Daily Scale Rainfall Series in the State of Zacatecas, Mexico. J. Appl. Meteor. Climatol. 2013, 52, 2771–2780. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Breslin, M.C.; Belward, J.A. Fractal Dimensions for Rainfall Time Series. Math. Comput. Simul. 1999, 48, 437–446. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civil Eng. 1951, 116, 770–799. [Google Scholar]
- Bo, Q.; Rashed, K. Hurst Exponent and Financial Market Predictability. In Proceedings of the IASTED Conference on Financial Engineering and Applications (FEA 2004), Cambridge, MA, USA, 8–10 November 2004; pp. 203–209. [Google Scholar]
- Chand, S.; Dixit, V.; Waller, S.T. Evaluation of Fluctuating Speed and Lateral Movement of Vehicles: Comparison between Mixed Traffic and Homogeneous Traffic. Transp. Res. Rec. J. Transp. Res. Board 2016, 2581, 104–112. [Google Scholar] [CrossRef]
- Chand, S.; Aouad, G.; Dixit, V.V. Long-Range Dependence of Traffic Flow and Speed of a Motorway. Transp. Res. Rec. J. Transp. Res. Board 2017, 2616, 49–57. [Google Scholar] [CrossRef]
- Rangarajan, G.; Sant, D.A. A Climate Predictability Index and Its Applications. Geophys. Res. Lett. 1997, 24, 1239–1242. [Google Scholar] [CrossRef]
- Matos, J.A.O.; Gama, S.M.A.; Ruskin, H.J.; Sharkasi, A.A.; Crane, M. Time and Scale Hurst Exponent Analysis for Financial Markets. Phys. A Stat. Mech. Appl. 2008, 387, 3910–3915. [Google Scholar] [CrossRef]
- Eom, C.; Choi, S.; Oh, G.; Jung, W.-S. Hurst Exponent and Prediction Based on Weak-Form Efficient Market Hypothesis of Stock Markets. Phys. A Stat. Mech. Appl. 2008, 387, 4630–4636. [Google Scholar] [CrossRef]
- Sobolev, D. The Effect of Price Volatility on Judgmental Forecasts: The Correlated Response Model. Int. J. Forecast. 2017, 33, 605–617. [Google Scholar] [CrossRef]
- DePetrillo, P.B.; Speers, D.; Ruttimann, U.E. Determining the Hurst Exponent of Fractal Time Series and Its Application to Electrocardiographic Analysis. Comput. Biol. Med. 1999, 29, 393–406. [Google Scholar] [CrossRef]
- Havlin, S.; Amaral, L.A.N.; Ashkenazy, Y.; Goldberger, A.L.; Ivanov, P.C.; Peng, C.-K.; Stanley, H.E. Application of Statistical Physics to Heartbeat Diagnosis. Phys. A Stat. Mech. Appl. 1999, 274, 99–110. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Z.; Liu, Y.; Wu, J.; Han, Y. Trend Analysis of Vegetation Dynamics in Qinghai–Tibet Plateau Using Hurst Exponent. Ecol. Indic. 2012, 14, 28–39. [Google Scholar] [CrossRef]
- Yulmetyev, R.; Gafarov, F.; Hänggi, P.; Nigmatullin, R.; Kayumov, S. Possibility Between Earthquake and Explosion Seismogram Differentiation by Discrete Stochastic Non-Markov Processes and Local Hurst Exponent Analysis. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2001, 64, 066132. [Google Scholar] [CrossRef]
- Baillie, R.T.; Chung, S.-K. Modeling and Forecasting from Trend-Stationary Long Memory Models with Applications to Climatology. Int. J. Forecast. 2002, 18, 215–226. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Turcotte, D.L. Long-Range Persistence in Climatological and Hydrological Time Series: Analysis, Modeling and Application to Drought Hazard Assessment. J. Hydrol. 1997, 203, 198–208. [Google Scholar] [CrossRef]
- Lan, L.W.; Lin, F.-Y.; Kuo, A.Y. Testing and Prediction of Traffic Flow Dynamics with Chaos. J. East. Asia Soc. Transp. Stud. 2003, 5, 1975–1990. [Google Scholar]
- Thomas, K.; Dia, H. Comparative Evaluation of Freeway Incident Detection Models Using Field Data. IEEE Proc. Intell. Transp. Syst. 2006, 153, 230–241. [Google Scholar] [CrossRef]
- Haleem, K.; Alluri, P.; Gan, A. Investigating Fractal Characteristics in Crash Trends for Potential Traffic Safety Prediction. In Proceedings of the Transportation Research Board 95th Annual Meeting, Washington, DC, USA, 10–14 January 2016. [Google Scholar]
- Chand, S.; Dixit, V.V. Application of Fractal Theory for Crash Rate Prediction: Insights from Random Parameters and Latent Class Tobit Models. Accid. Anal. Prev. 2018, 112, 30–38. [Google Scholar] [CrossRef]
- Xu, P.; Huang, H. Modeling Crash Spatial Heterogeneity: Random Parameter Versus Geographically Weighting. Accid. Anal. Prev. 2015, 75, 16–25. [Google Scholar] [CrossRef]
- Coruh, E.; Bilgic, A.; Tortum, A. Accident Analysis with Aggregated Data: The Random Parameters Negative Binomial Panel Count Data Model. Anal. Methods Accid. Res. 2015, 7, 37–49. [Google Scholar] [CrossRef]
- Truong, L.T.; Kieu, L.-M.; Vu, T.A. Spatiotemporal and Random Parameter Panel Data Models of Traffic Crash Fatalities in Vietnam. Accid. Anal. Prev. 2016, 94, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Chand, S.; Moylan, E.; Waller, S.T.; Dixit, V. Analysis of Vehicle Breakdown Frequency: A Case Study of New South Wales, Australia. Sustainability 2020, 12, 8244. [Google Scholar] [CrossRef]
- Lord, D.; Mannering, F. The Statistical Analysis of Crash-Frequency Data: A Review and Assessment of Methodological Alternatives. Transp. Res. Part A Policy Pract. 2010, 44, 291–305. [Google Scholar] [CrossRef]
- Shugan, S.M. Editorial: Errors in the Variables, Unobserved Heterogeneity, and Other Ways of Hiding Statistical Error. Mark. Sci. 2006, 25, 203–216. [Google Scholar] [CrossRef]
- Washington, S.P.; Karlaftis, M.G.; Mannering, F. Statistical and Econometric Methods for Transportation Data Analysis; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Chen, E.; Tarko, A.P. Modeling Safety of Highway Work Zones with Random Parameters and Random Effects Models. Anal. Methods Accid. Res. 2014, 1, 86–95. [Google Scholar] [CrossRef]
- Pande, A.; Chand, S.; Saxena, N.; Dixit, V.; Loy, J.; Wolshon, B.; Kent, J.D. A Preliminary Investigation of the Relationships between Historical Crash and Naturalistic Driving. Accid. Anal. Prev. 2017, 101, 107–116. [Google Scholar] [CrossRef]
- Greene, W.H. LIMDEP, Version 11.0; Econometric Software Inc.: Plainview, NY, USA, 2016. [Google Scholar]
- Grattan Institute Mapping Australia’s Economy: Cities as Engines of Prosperity; Grattan Institute: Melbourne, Australia, 2014.
- TomTom Full Ranking|TomTom Traffic Index. Available online: https://www.tomtom.com/en_gb/traffic-index/ranking/ (accessed on 28 November 2019).
- Lowrie, P.R. The Sydney Coordinated Adaptive Traffic System—Principles, Methodology, Algorithms. In Proceedings of the International Conference on Road Traffic Signalling, London, UK, 30 March–1 April 1982. [Google Scholar]
- Yu, X.-H.; Recker, W.W. Stochastic Adaptive Control Model for Traffic Signal Systems. Transp. Res. Part C Emerg. Technol. 2006, 14, 263–282. [Google Scholar] [CrossRef]
- Weijermars, W.; Berkum, E. van Analyzing Highway Flow Patterns Using Cluster Analysis. In Proceedings of the 2005 IEEE Intelligent Transportation Systems, Vienna, Austria, 13–16 September 2005; pp. 308–313. [Google Scholar]
- Keay, K.; Simmonds, I. The Association of Rainfall and Other Weather Variables with Road Traffic Volume in Melbourne, Australia. Accid. Anal. Prev. 2005, 37, 109–124. [Google Scholar] [CrossRef]
- Tsirigotis, L.; Vlahogianni, E.I.; Karlaftis, M.G. Does Information on Weather Affect the Performance of Short-Term Traffic Forecasting Models? Int. J. ITS Res. 2012, 10, 1–10. [Google Scholar] [CrossRef]
- Chung, E.; Ohtani, O.; Warita, H.; Kuwahara, M.; Morita, H. Effect of Rain on Travel Demand and Traffic Accidents. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Vienna, Austria, 13–16 September 2005; pp. 1080–1083. [Google Scholar]
- Sabir, M.; Ommeren, J.; Koetse, M.J.; Rietveld, P. Impact of Weather on Daily Travel Demand; Department of Spatial Economics, VU University: Amsterdam, The Netherlands, 2010. [Google Scholar]

| Type of Day | Count | Type of Variable | % of Observations (Categorical Variables) | For Continuous Variables | |||
|---|---|---|---|---|---|---|---|
| Mean | Std. Dev. | Max | Min | ||||
| Day of week | |||||||
| Monday | 52 | TV | 14.29 | ||||
| Tuesday | 52 | TV | 14.29 | ||||
| Wednesday | 52 | TV | 14.29 | ||||
| Thursday | 52 | TV | 14.29 | ||||
| Friday | 52 | TV | 14.29 | ||||
| Saturday | 52 | TV | 14.29 | ||||
| Sunday | 52 | TV | 14.29 | ||||
| Type of day | |||||||
| Public holiday | 11 | TV | 3.02 | ||||
| Special event day | 33 | TV | 9.07 | ||||
| Season | |||||||
| Spring | 90 | TV | 24.73 | ||||
| Autumn | 92 | TV | 25.27 | ||||
| Winter | 92 | TV | 25.27 | ||||
| Summer | 90 | TV | 24.73 | ||||
| Rainfall (mm) | 364 | TV | 3.65 | 10.27 | 116.02 | 0 | |
| Temperature (°C) | 364 | TV | 19.03 | 4.44 | 29.2 | 9.6 | |
| Average Annual Daily Traffic (AADT) | 37 | SV | 36,360 | 15,772 | 64,189 | 7237 | |
| Lanes | 37 | SV | 9.54 | 3.33 | 16 | 3 | |
| ≤8 lanes | 7 | SV | 18.92 | ||||
| 8–12 lanes | 23 | SV | 62.16 | ||||
| >12 lanes | 7 | SV | 18.92 | ||||
| Approaches | 37 | SV | 3.43 | 0.59 | 4 | 1 | |
| 1, 2 | 2 | SV | 5.41 | ||||
| 3 | 17 | SV | 45.95 | ||||
| 4 | 18 | SV | 48.64 | ||||
| Parking lanes | 37 | SV | 1.35 | 1.07 | 4 | 0 | |
| No parking | 10 | SV | 27.03 | ||||
| 1–2 lanes | 22 | SV | 59.46 | ||||
| 3–4 lanes | 5 | SV | 13.51 | ||||
| Bus stops | 37 | SV | 1.27 | 1.22 | 5 | 0 | |
| No bus stop | 12 | SV | 32.43 | ||||
| 1–2 bus stops | 20 | SV | 54.05 | ||||
| 3,4, and 5 bus stops | 5 | SV | 13.51 | ||||
| Crashes | 37 | SV | 18.16 | 14.70 | 72 | 1 | |
| Variable | Coefficient | Robust Std. Error | Z | p >|z| |
|---|---|---|---|---|
| Day of the week | ||||
| Monday | Base | |||
| Tuesday | 0.0135 | 0.0027 | 4.98 | <0.01 |
| Wednesday | 0.0276 | 0.0037 | 7.41 | <0.01 |
| Thursday | 0.0367 | 0.0046 | 7.90 | <0.01 |
| Friday | 0.0642 | 0.0064 | 10.02 | <0.01 |
| Saturday | 0.1336 | 0.0086 | 15.52 | <0.01 |
| Sunday | 0.1035 | 0.0063 | 16.55 | <0.01 |
| Type of day | ||||
| Special event day | 0.0119 | 0.0018 | 6.47 | <0.01 |
| Public holiday | 0.0705 | 0.0057 | 12.42 | <0.01 |
| Weather | ||||
| Rainfall (in 10 mm) | −0.0049 | 0.0007 | −6.43 | <0.01 |
| Temperature (in 10 °C) | 0.0093 | 0.0021 | 4.49 | <0.01 |
| Parking | ||||
| No parking | Base | |||
| 1–2 lanes | Insignificant | |||
| 3–4 lanes | 0.0680 | 0.0209 | 3.25 | <0.01 |
| Constant | 0.7675 | 0.0128 | 60.03 | |
| Sigma_u | 0.0404 | |||
| Sigma_e | 0.0422 | |||
| Rho | 0.4781 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chand, S. Modeling Predictability of Traffic Counts at Signalised Intersections Using Hurst Exponent. Entropy 2021, 23, 188. https://doi.org/10.3390/e23020188
Chand S. Modeling Predictability of Traffic Counts at Signalised Intersections Using Hurst Exponent. Entropy. 2021; 23(2):188. https://doi.org/10.3390/e23020188
Chicago/Turabian StyleChand, Sai. 2021. "Modeling Predictability of Traffic Counts at Signalised Intersections Using Hurst Exponent" Entropy 23, no. 2: 188. https://doi.org/10.3390/e23020188
APA StyleChand, S. (2021). Modeling Predictability of Traffic Counts at Signalised Intersections Using Hurst Exponent. Entropy, 23(2), 188. https://doi.org/10.3390/e23020188





