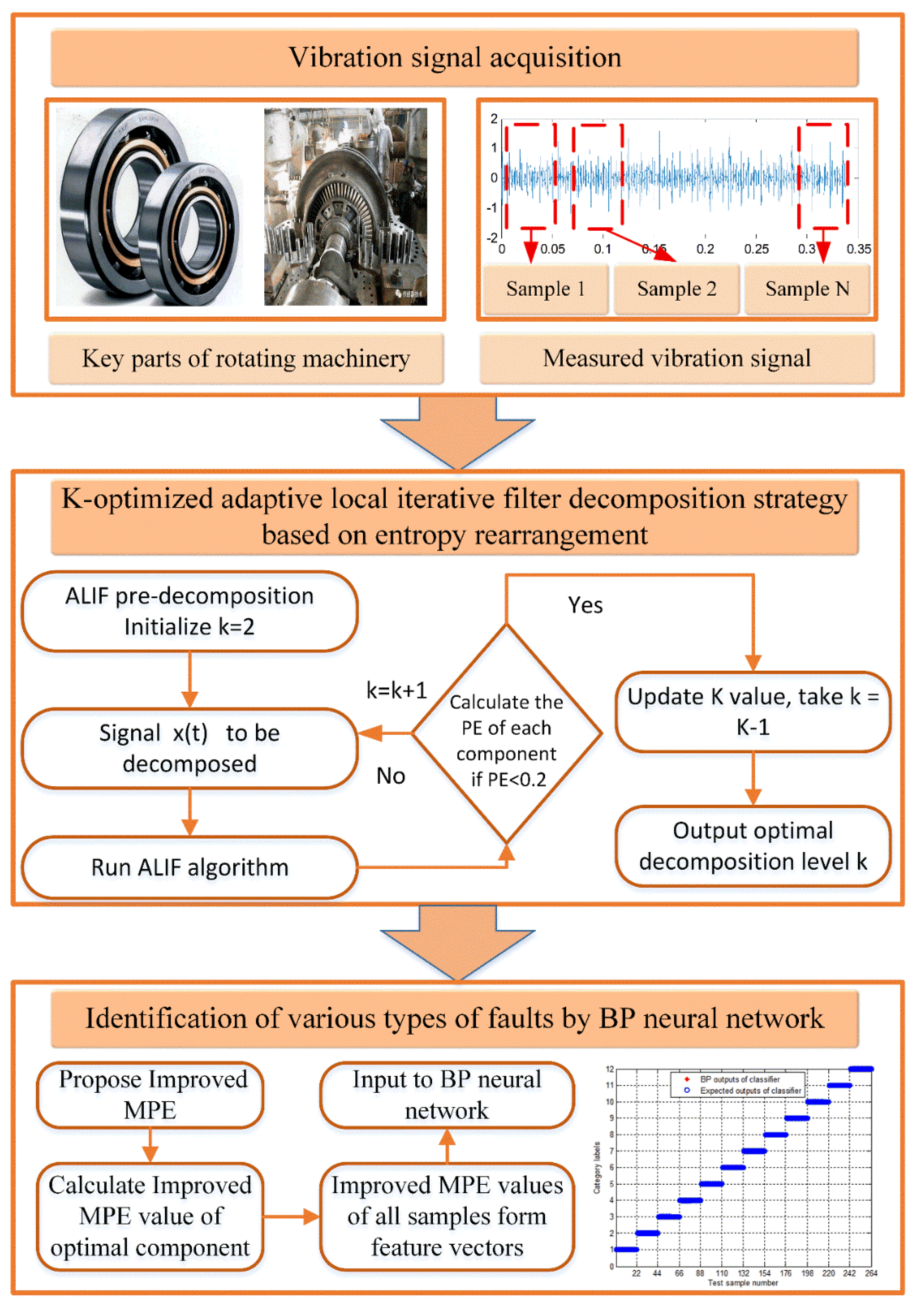
A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy
Abstract
:1. Introduction
2. Theoretical Description
2.1. Adaptive Local Iterative Filtering
- (1)
- Over the entire signal length, the number of extreme points and the number of zero crossings must differ by one or the same.
- (2)
- The average value of the obtained upper envelope and lower envelope is zero.
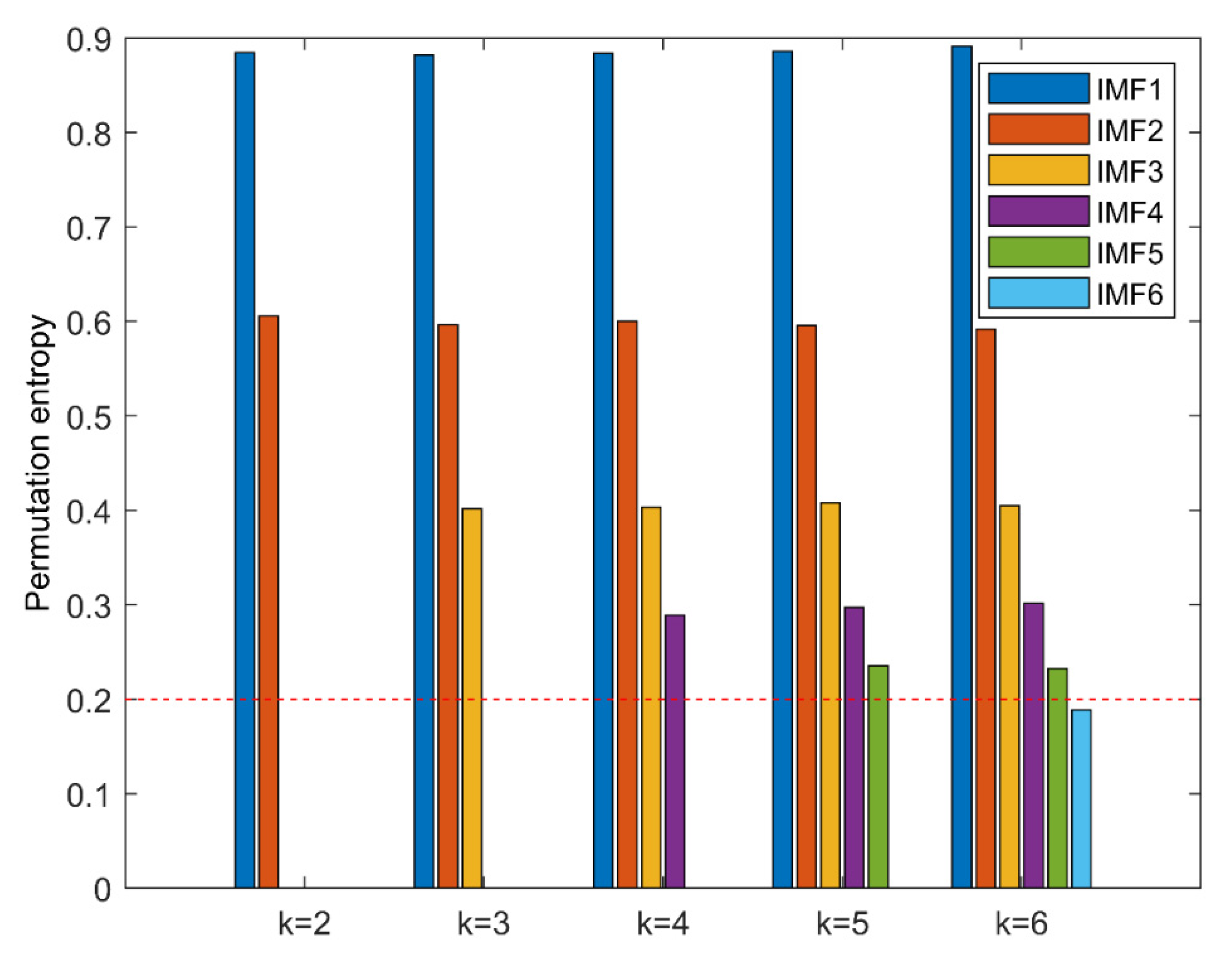
2.2. K-Optimized ALIF Based on PE
3. Improved Multiscale Permutation Entropy
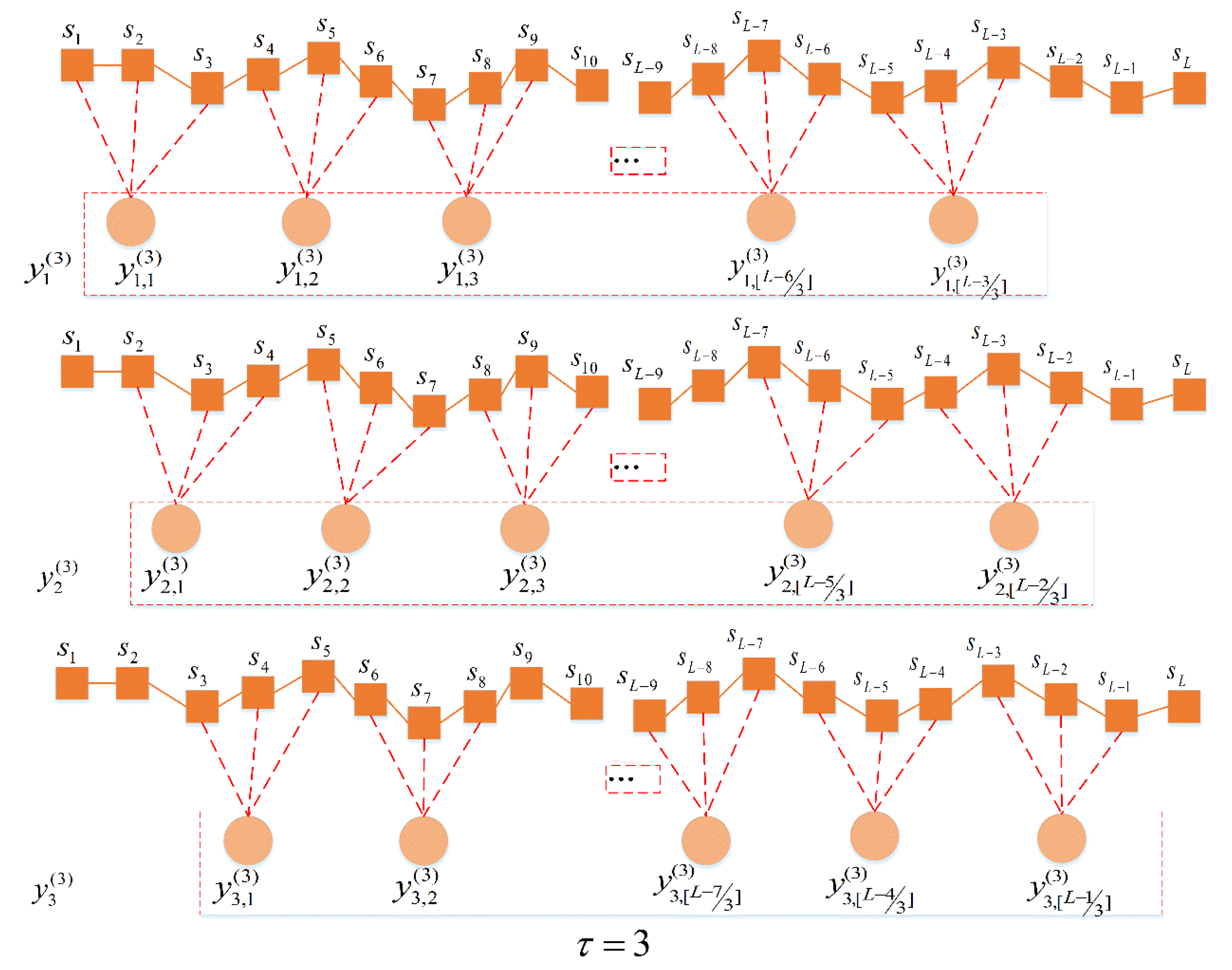
3.1. Multiscale Permutation Entropy
3.2. Improved Multiscale Permutation Entropy (Improved MPE)
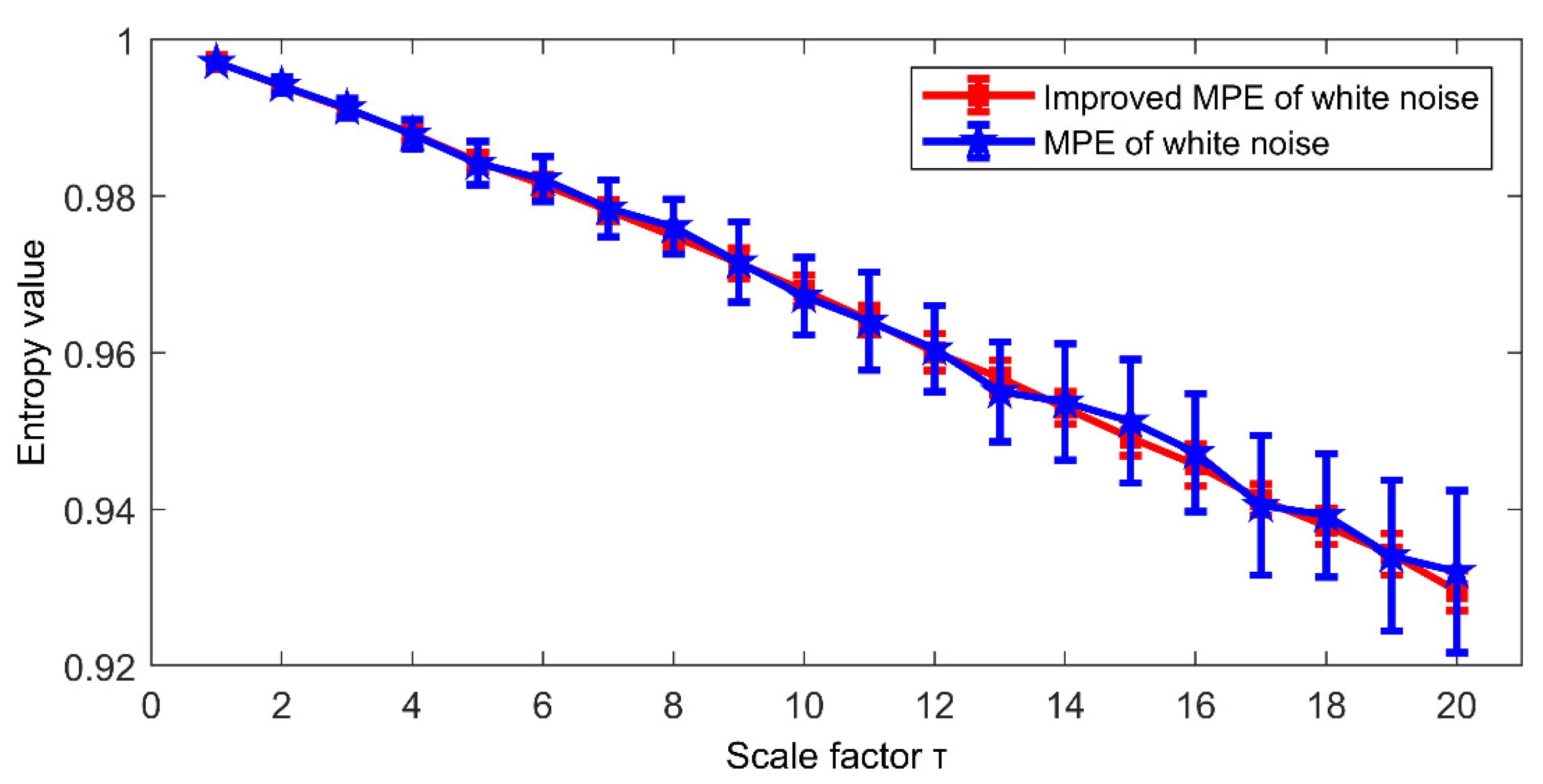
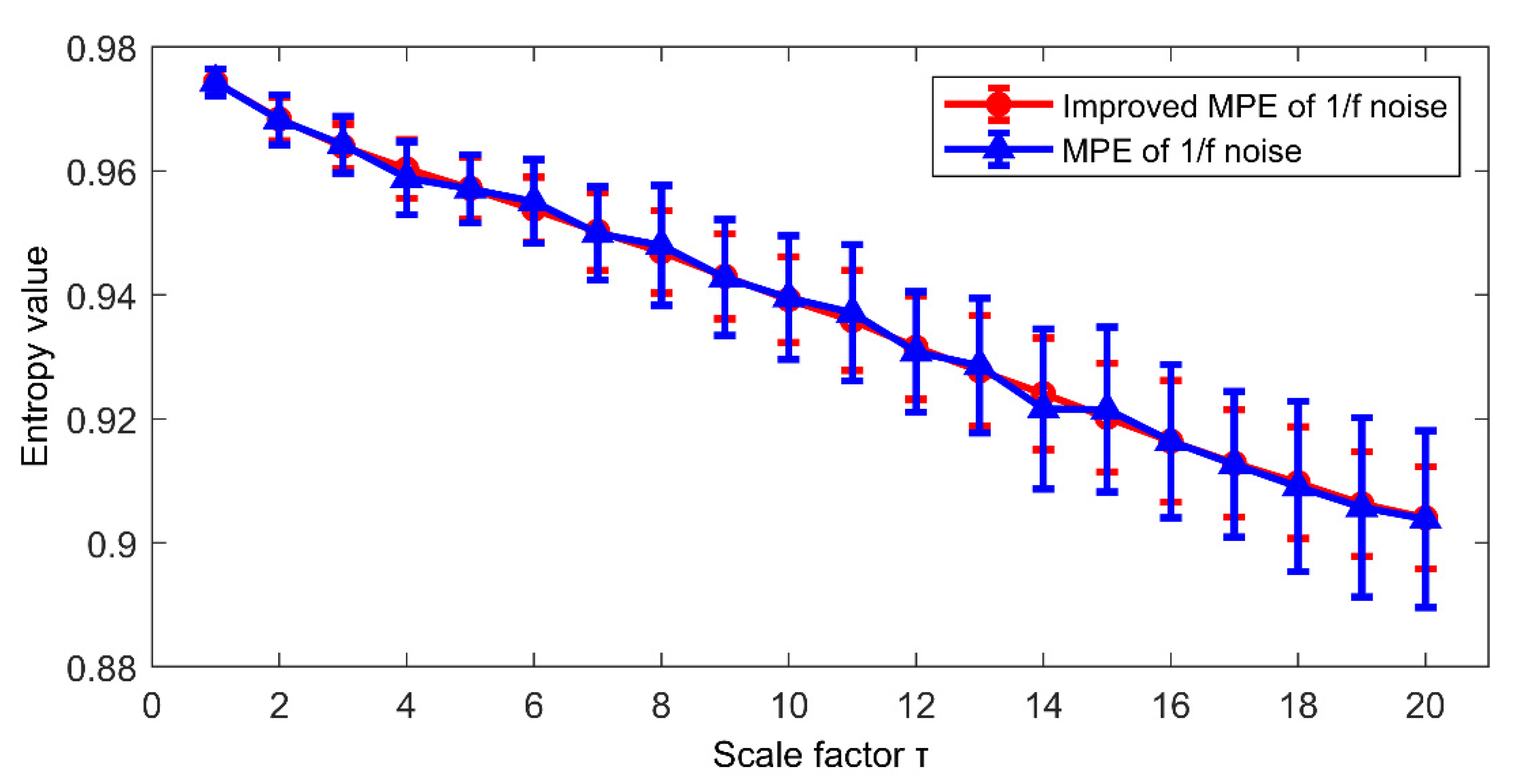
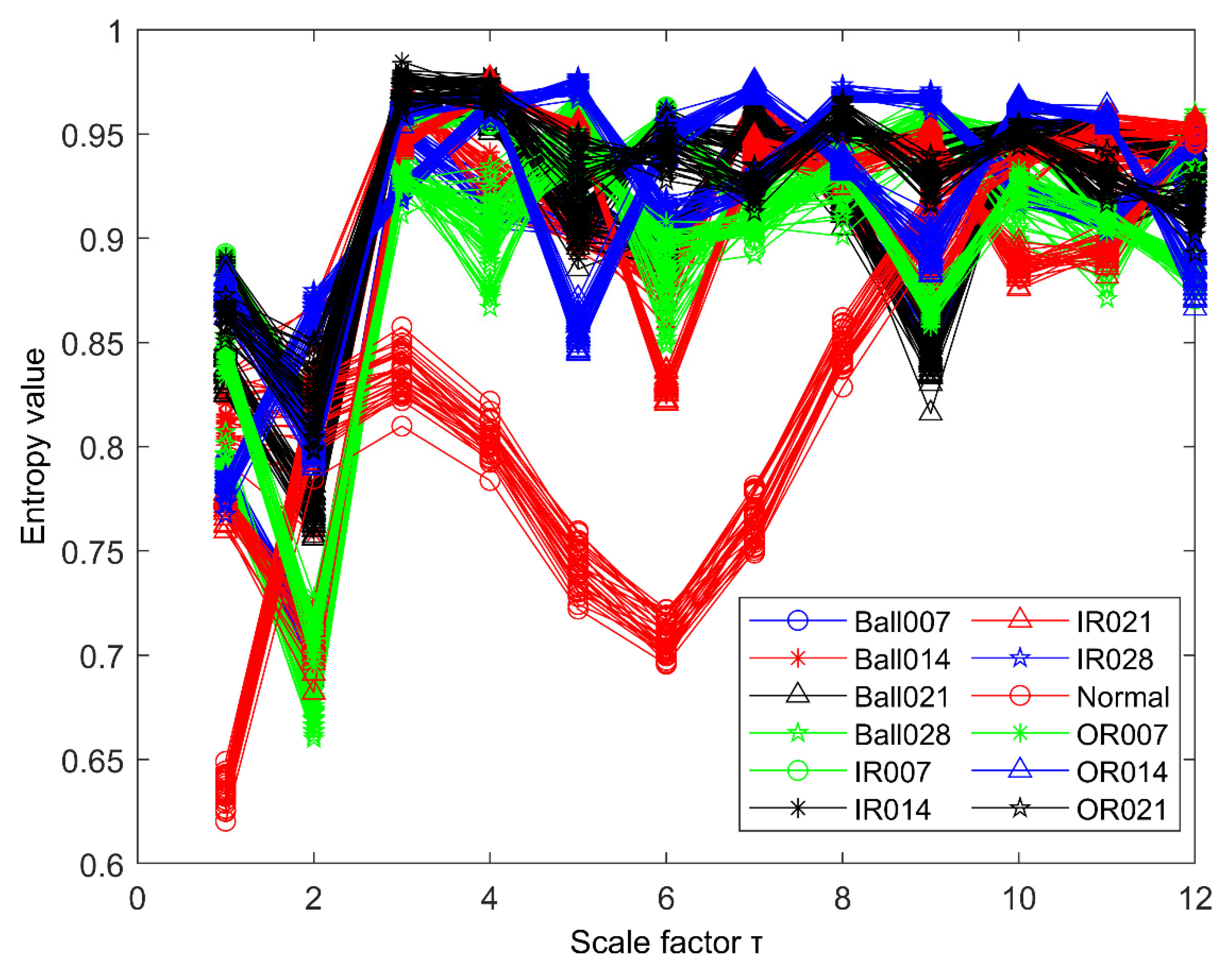
3.3. Performance Comparison between MPE and Improved MPE
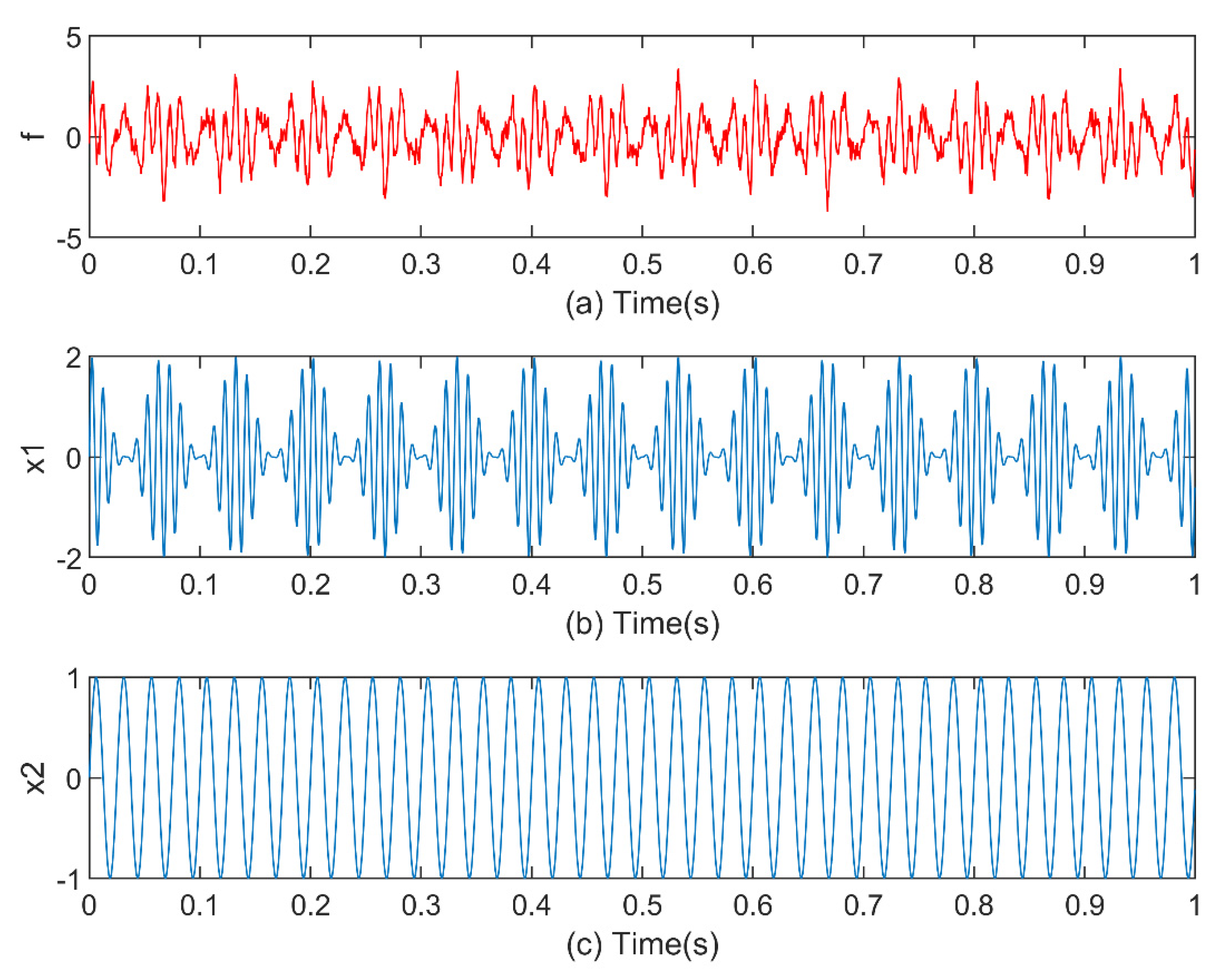
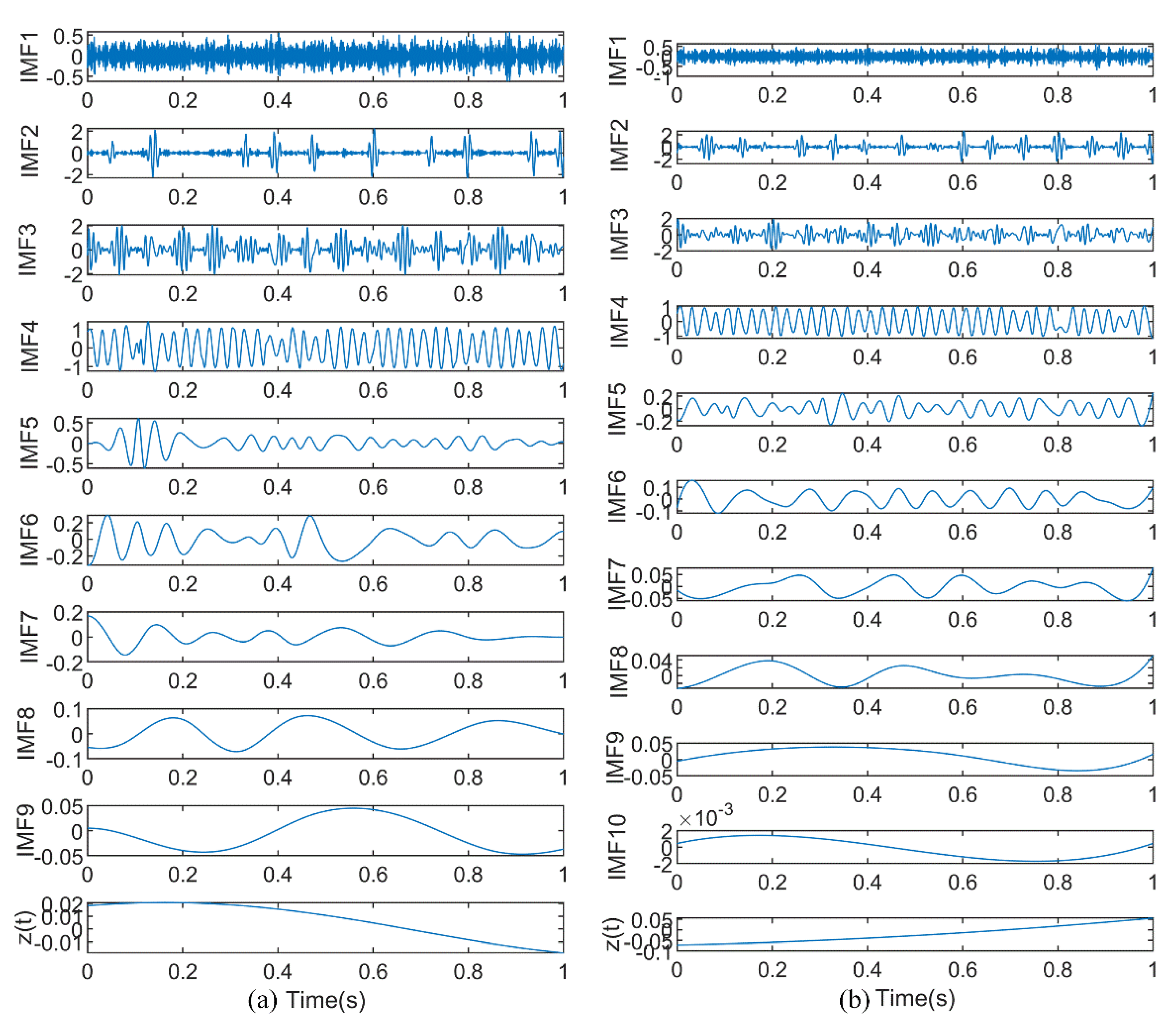
4. Numerical Simulation Analysis
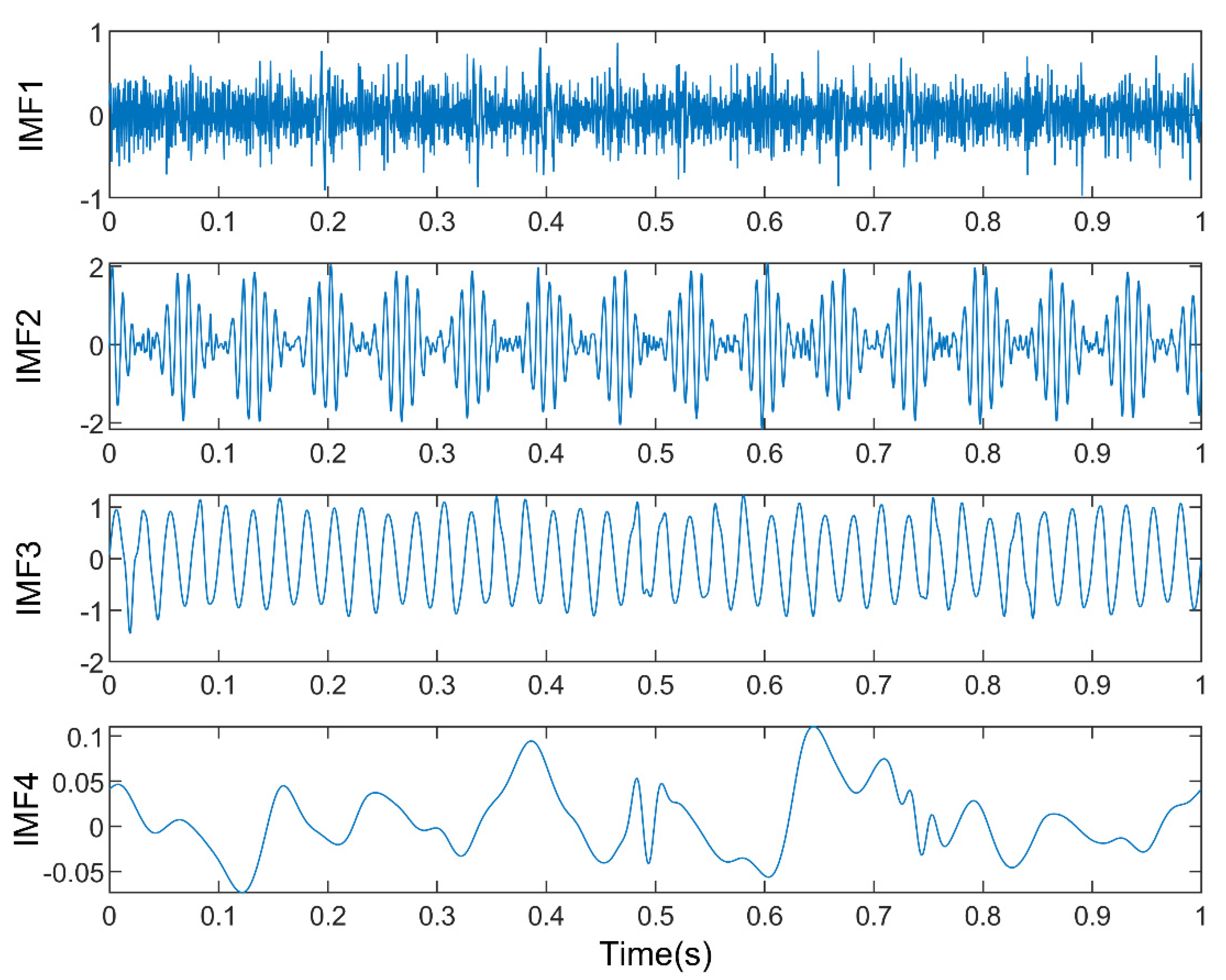
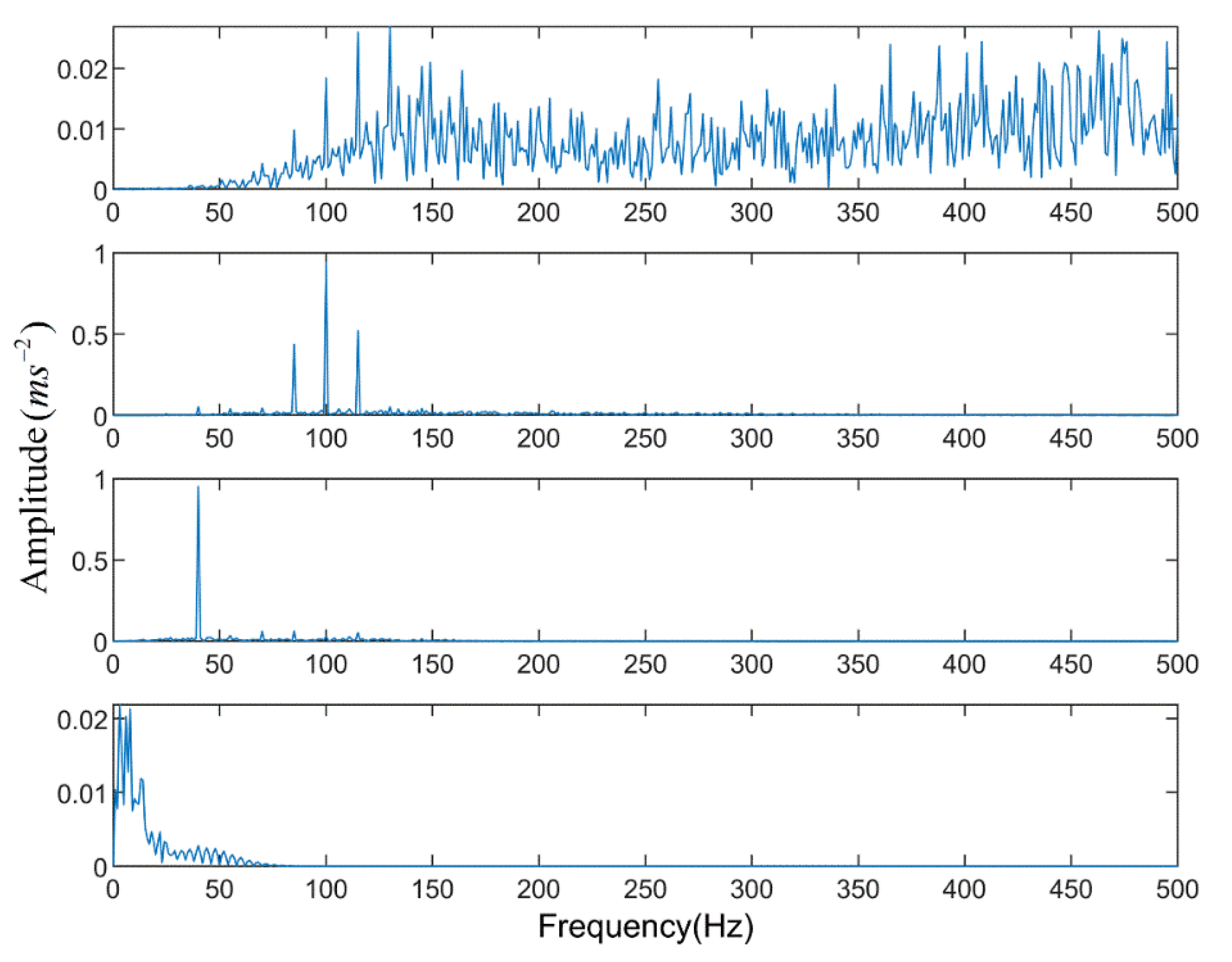
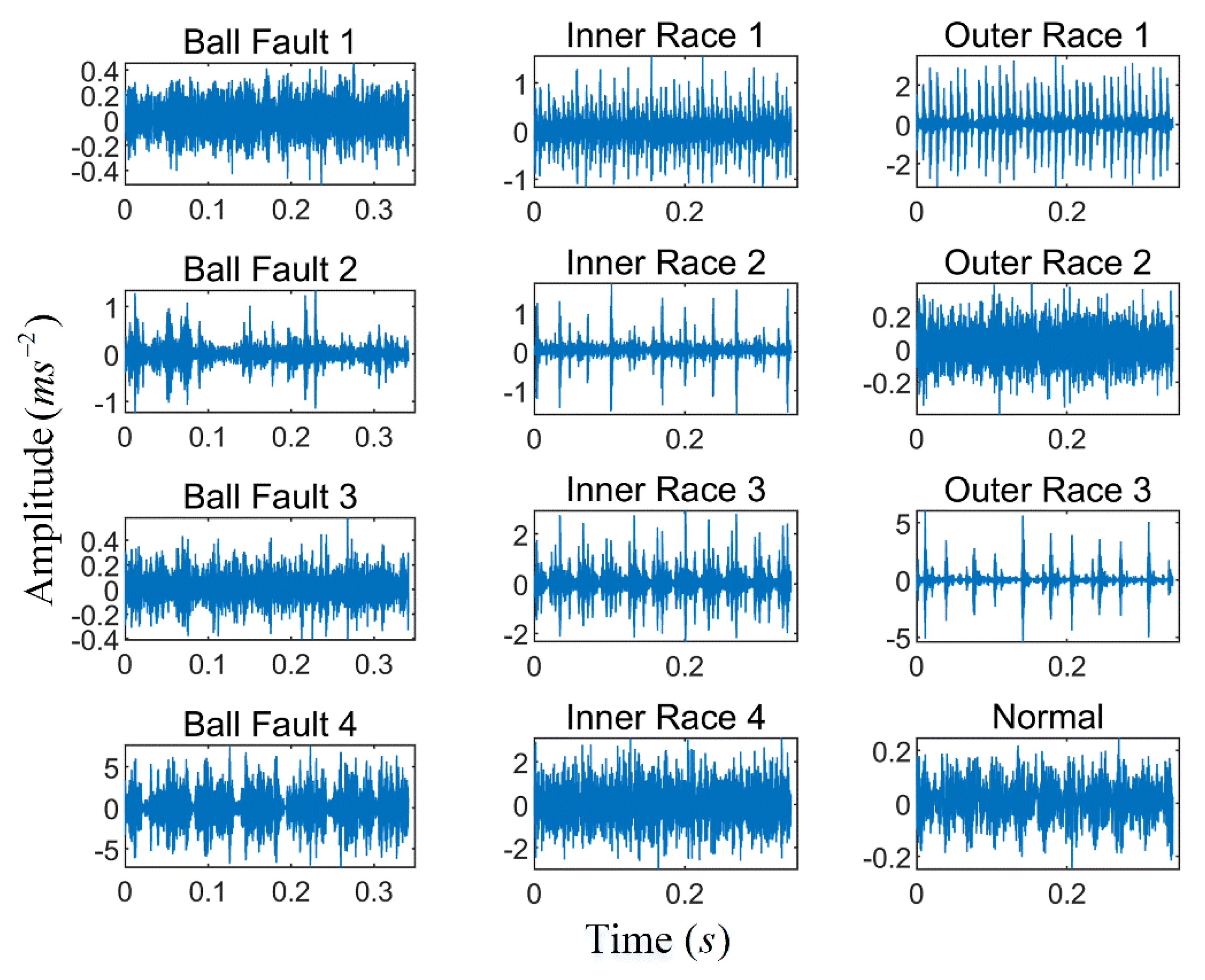
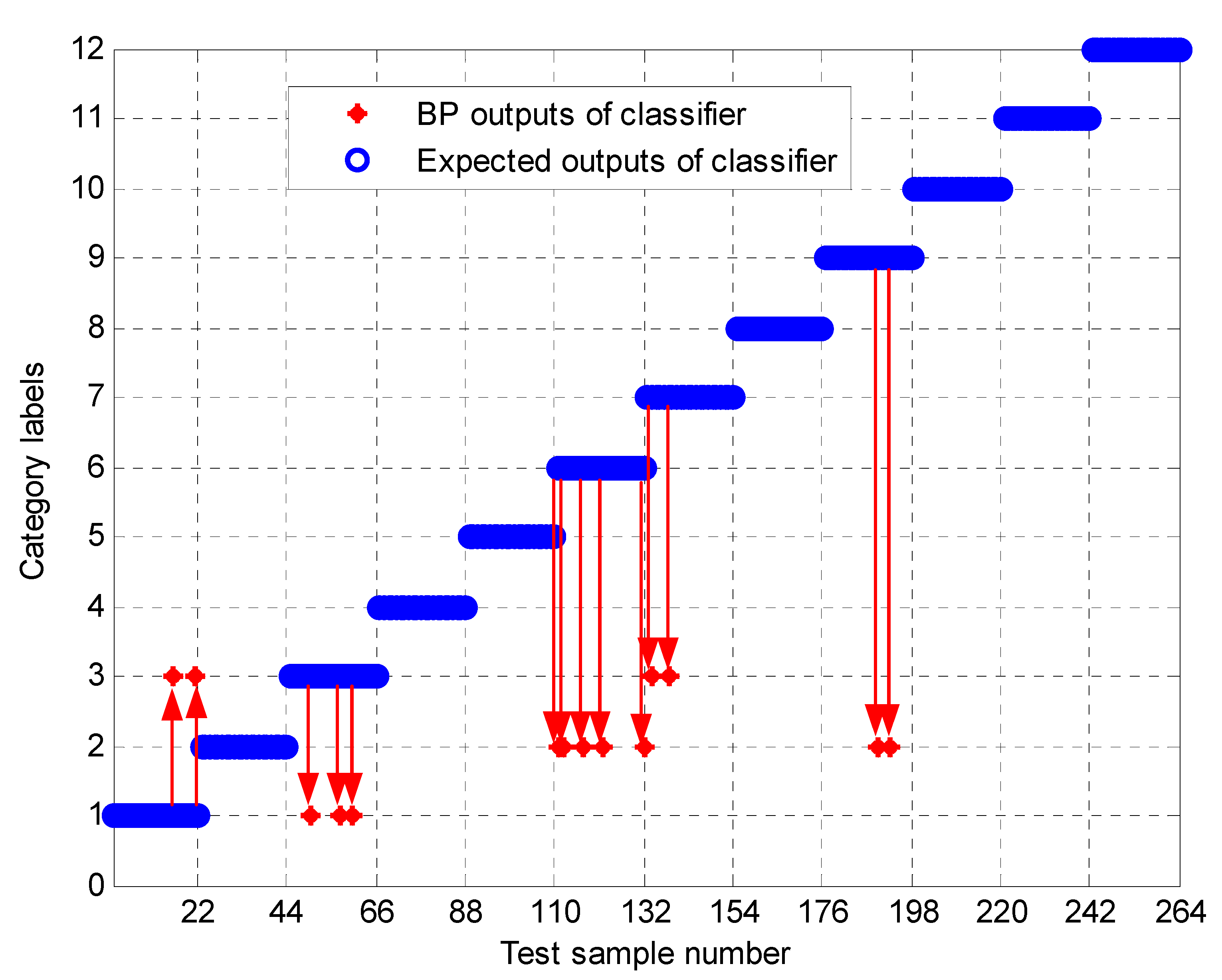
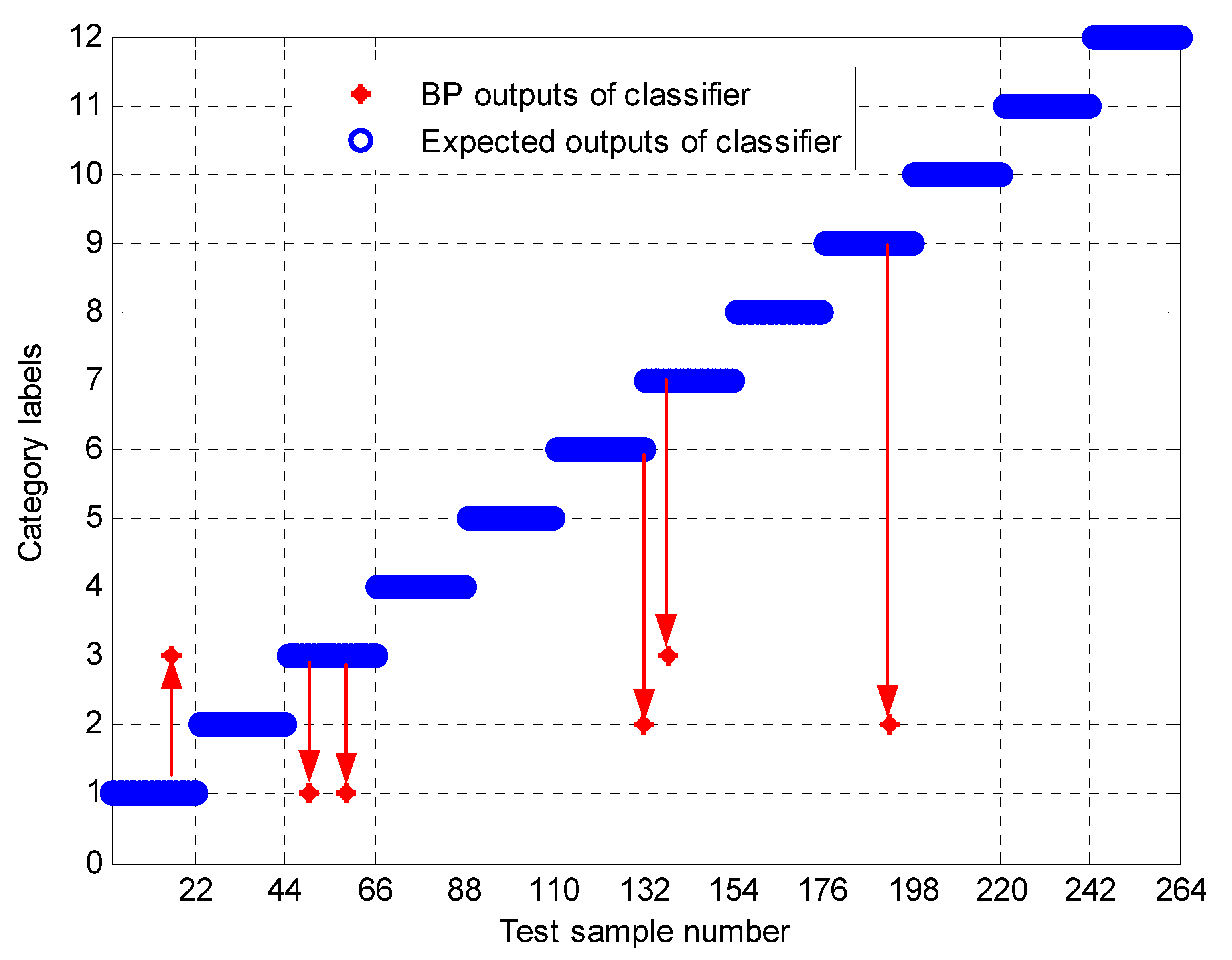
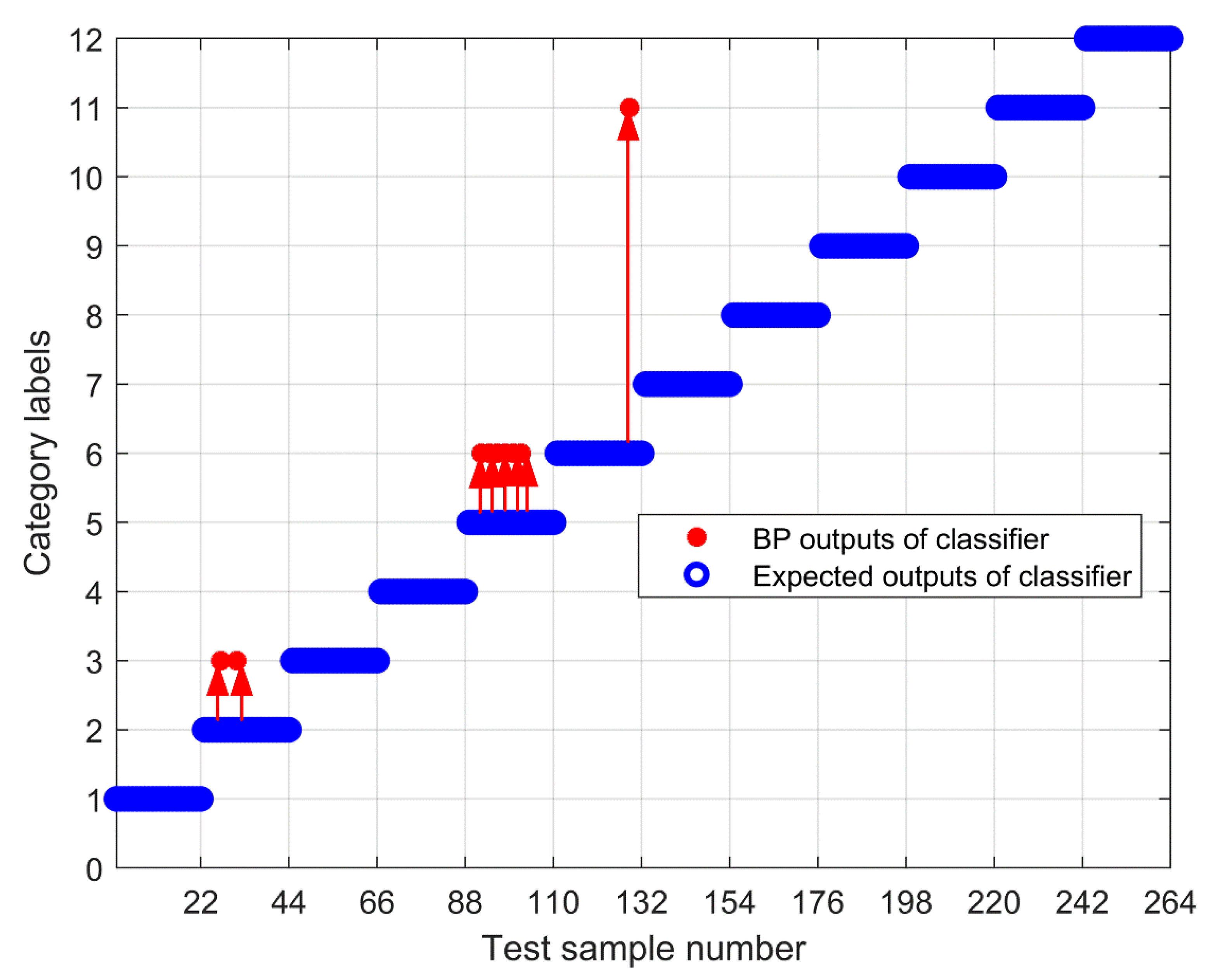
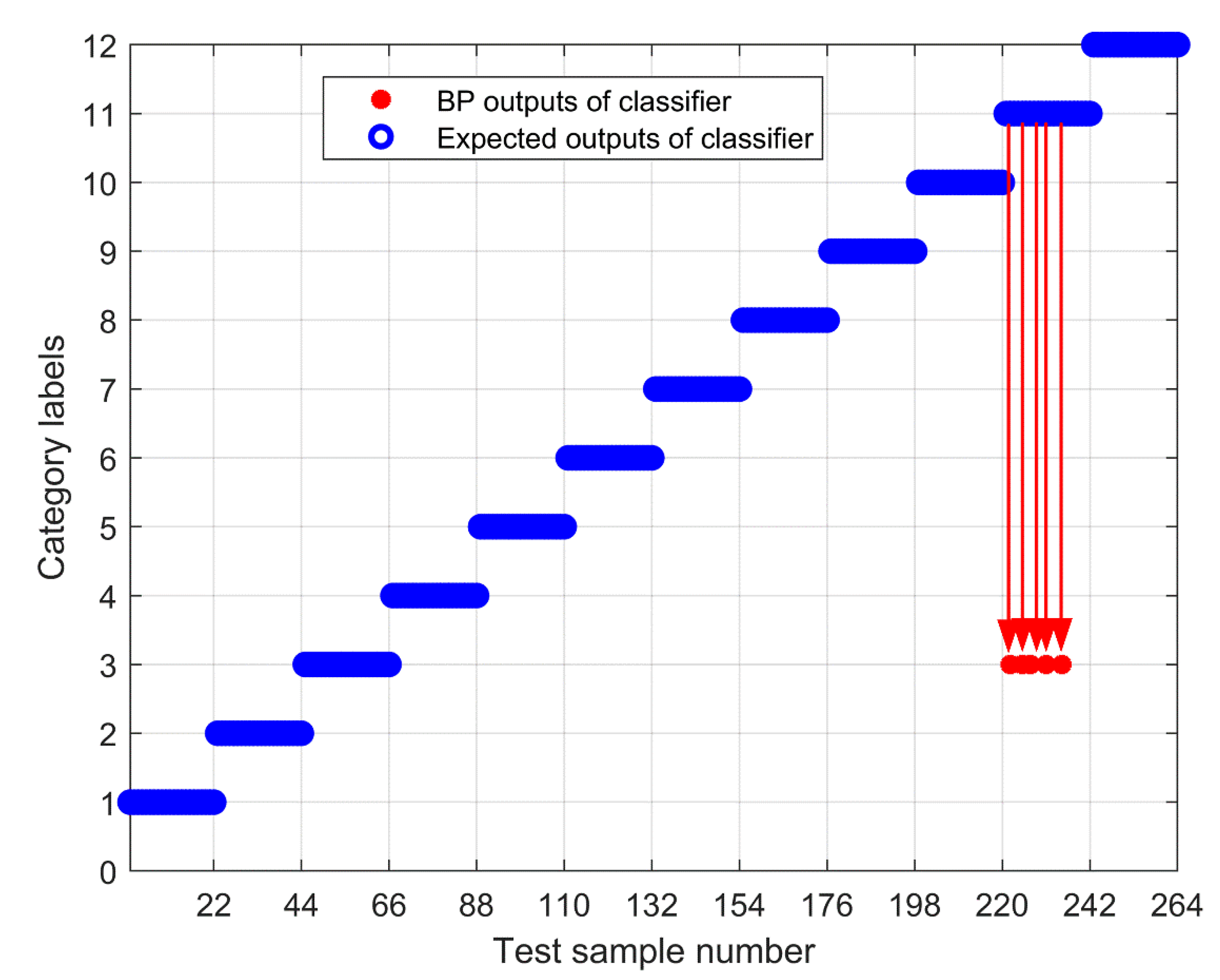
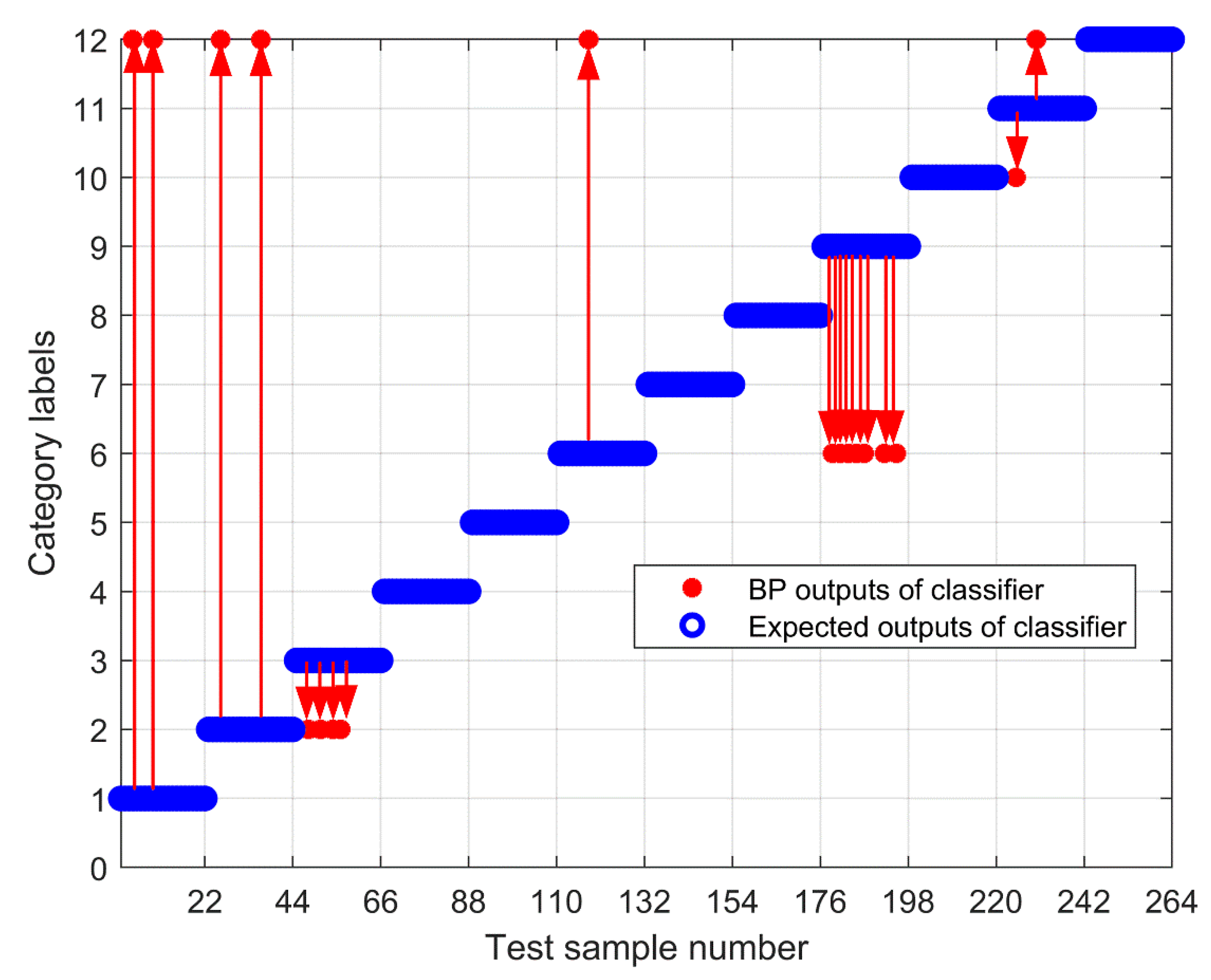
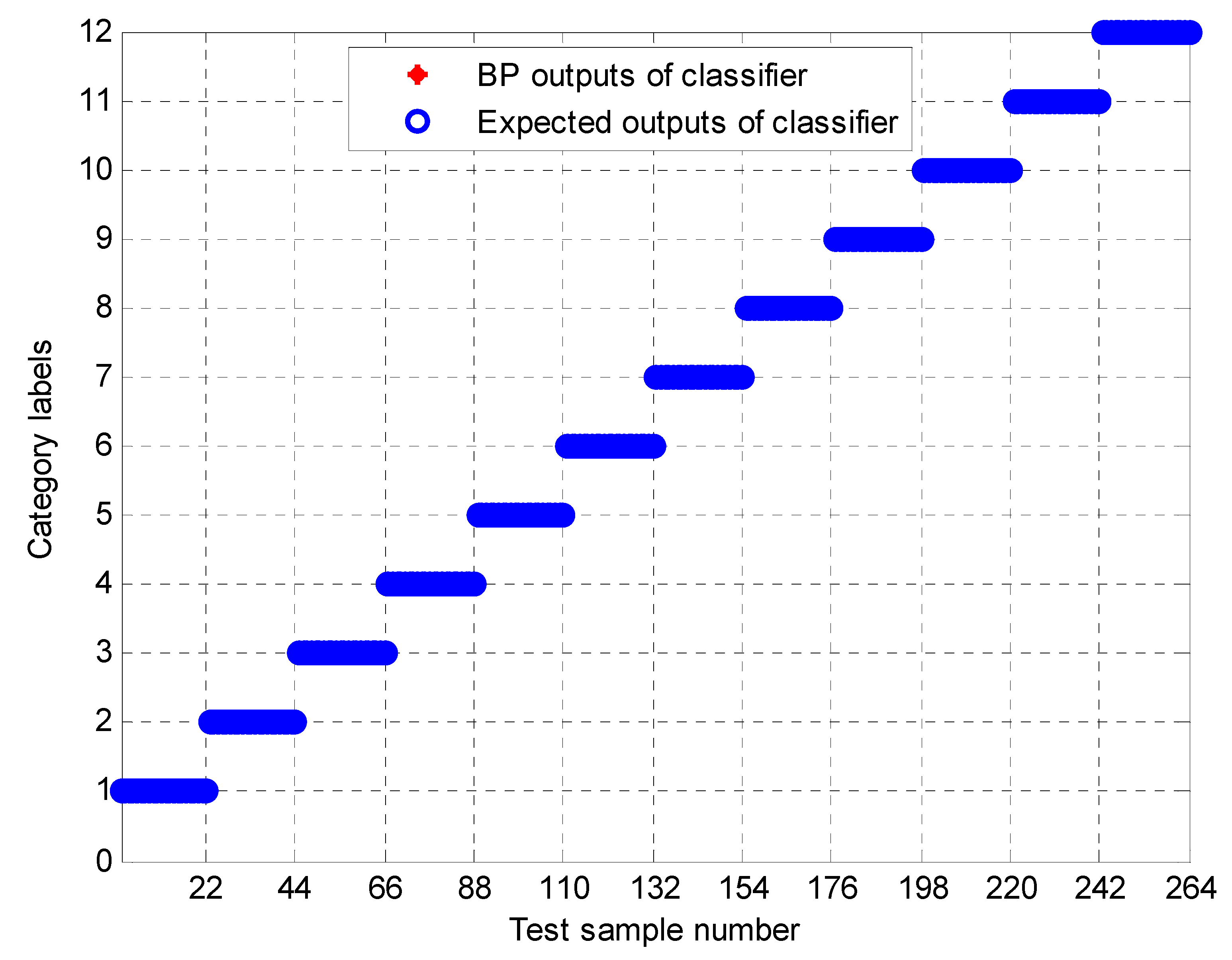
5. Experimental Study
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H. Mean-optimized mode decomposition: An improved EMD approach for non-stationary signal processing. Isa Trans. 2020, 106, 392–401. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Wang, Z.Y.; Qin, W.L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H. Use of generalized refined composite multiscale fractional dispersion entropy to diagnose the faults of rolling bearing. Nonlinear Dyn. 2020, 101, 1417–1440. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. EEMD method and WNN for fault diagnosis of locomotive roller bearings. Expert Syst. Appl. 2011, 38, 7334–7341. [Google Scholar] [CrossRef]
- Chine, W.; Mellit, A.; Lughi, V.; Malek, A.; Sulligoi, G.; Pavan, A.M. A novel fault diagnosis technique for photovoltaic systems based on artificial neural networks. Renew. Energy 2016, 90, 501–512. [Google Scholar] [CrossRef]
- Song, L.; Wang, H.; Chen, P. Vibration-based intelligent fault diagnosis for roller bearings in low-speed rotating machinery. IEEE Trans. Instrum. Meas. 2018, 67, 1887–1899. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Li, C.; Sánchez, R.-V.; Zurita, G.; Cerrada, M.; Cabrera, D. Fault diagnosis for rotating machinery using vibration measurement deep statistical feature learning. Sensors 2016, 16, 895. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Fan, F.; Zhou, K.; He, Z. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Lin, Y.; Li, X. A novel method for intelligent fault diagnosis of rolling bearings using ensemble deep auto-encoders. Mech. Syst. Signal Process. 2018, 102, 278–297. [Google Scholar] [CrossRef]
- Yang, J.; Huang, D.; Zhou, D.; Liu, H. Optimal IMF selection and unknown fault feature extraction for rolling bearings with different defect modes. Measurement 2020, 107660. [Google Scholar] [CrossRef]
- Aubel, C.; Stotz, D.; Bölcskei, H. A theory of super-resolution from short-time Fourier transform measurements. J. Fourier Anal. Appl. 2018, 24, 45–107. [Google Scholar] [CrossRef] [Green Version]
- Ouelha, S.; Touati, S.; Boashash, B. An efficient inverse short-time Fourier transform algorithm for improved signal reconstruction by time-frequency synthesis: Optimality and computational issues. Digit. Signal Process. 2017, 65, 81–93. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70, 1–35. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A comparative study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to bearing defect diagnosis. Mech. Syst. Signal Process. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. Bearing performance degradation assessment based on a combination of empirical mode decomposition and k-medoids clustering. Mech. Syst. Signal Process. 2017, 93, 16–29. [Google Scholar] [CrossRef]
- Imaouchen, Y.; Kedadouche, M.; Alkama, R.; Thomas, M. A frequency-weighted energy operator and complementary ensemble empirical mode decomposition for bearing fault detection. Mech. Syst. Signal Process. 2017, 82, 103–116. [Google Scholar] [CrossRef]
- Xu, F.; Song, X.; Tsui, K.-L.; Yang, F.; Huang, Z. Bearing performance degradation assessment based on ensemble empirical mode decomposition and affinity propagation clustering. IEEE Access 2019, 7, 54623–54637. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Haiyang, Z.; Jindong, W.; Lee, J.; Ying, L. A compound interpolation envelope local mean decomposition and its application for fault diagnosis of reciprocating compressors. Mech. Syst. Signal. Process. 2018, 110, 273–295. [Google Scholar] [CrossRef]
- Cicone, A.; Liu, J.; Zhou, H. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmon. Anal. 2016, 41, 384–411. [Google Scholar] [CrossRef] [Green Version]
- Piersanti, M.; Materassi, M.; Cicone, A.; Spogli, L.; Zhou, H.; Ezquer, R.G. Adaptive local iterative filtering: A promising technique for the analysis of nonstationary signals. J. Geophys. Res. Space Phys. 2018, 123, 1031–1046. [Google Scholar] [CrossRef] [Green Version]
- Cicone, A.; Dell’Acqua, P. Study of boundary conditions in the iterative filtering method for the decomposition of nonstationary signals. J. Comput. Appl. Math. 2020, 373, 112248. [Google Scholar] [CrossRef] [Green Version]
- Cicone, A.; Garoni, C.; Serra-Capizzano, S. Spectral and convergence analysis of the Discrete ALIF method. Linear Algebra Appl. 2019, 580, 62–95. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Malekjafarian, A.; González, A. Application of empirical mode decomposition to drive-by bridge damage detection. Eur. J. Mech. A/Solids 2017, 61, 151–163. [Google Scholar] [CrossRef]
- Lv, Y.; Zhang, Y.; Yi, C. Optimized adaptive local iterative filtering algorithm based on permutation entropy for rolling bearing fault diagnosis. Entropy 2018, 20, 920. [Google Scholar] [CrossRef] [Green Version]
- Bandt, C. Permutation Entropy and Order Patterns in Long Time Series. In Time Series Analysis and Forecasting; Springer: Cham, Germany, 2016; pp. 61–73. [Google Scholar]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Methods Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef]
- Zheng, J.; Dong, Z.; Pan, H.; Ni, Q.; Zhang, J. Composite multi-scale weighted permutation entropy and extreme learning machine based intelligent fault diagnosis for rolling bearing. Measurement 2019, 143, 69–80. [Google Scholar] [CrossRef]
- Xue, X.; Li, C.; Cao, S.; Sun, J.; Liu, L. Fault diagnosis of rolling element bearings with a two-step scheme based on permutation entropy and random forests. Entropy 2019, 21, 96. [Google Scholar] [CrossRef] [Green Version]
- Berger, S.; Schneider, G.; Kochs, E.F.; Jordan, D. Permutation Entropy: Too Complex a Measure for EEG Time Series? Entropy 2017, 19, 692. [Google Scholar] [CrossRef] [Green Version]
- Zhu, K.; Chen, L.; Hu, X. Rolling element bearing fault diagnosis by combining adaptive local iterative filtering, improved fuzzy entropy and support vector machine. Entropy 2018, 20, 926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, K.; Song, X.; Xue, D. A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm. Measurement 2014, 47, 669–675. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Wang, F.; Wang, Y. Rolling bearing fault diagnosis using adaptive deep belief network with dual-tree complex wavelet packet. ISA Trans. 2017, 69, 187–201. [Google Scholar] [CrossRef] [PubMed]
- Olivares, F.; Zunino, L.; Gulich, D.; Pérez, D.G.; Rosso, O.A. Multiscale permutation entropy analysis of laser beam wandering in isotropic turbulence. Phys. Rev. E 2017, 96, 042207. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Pan, H.; Yang, S.; Cheng, J. Generalized composite multiscale permutation entropy and Laplacian score based rolling bearing fault diagnosis. Mech. Syst. Signal. Process. 2018, 99, 229–243. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Zhao, Y.; Pan, G. Wind speed prediction of IPSO-BP neural network based on lorenz disturbance. IEEE Access 2018, 6, 53168–53179. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Jha, R.K. A novel noise-enhanced back-propagation technique for weak signal detection in Neyman–Pearson framework. Neural Process. Lett. 2019, 50, 2389–2406. [Google Scholar] [CrossRef]
- Ciabattoni, L.; Ferracuti, F.; Freddi, A.; Monteriu, A. Statistical Spectral Analysis for Fault Diagnosis of Rotating Machines. IEEE Trans. Ind. Ind. Electron. 2018, 65, 4301–4310. [Google Scholar] [CrossRef]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal. Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]





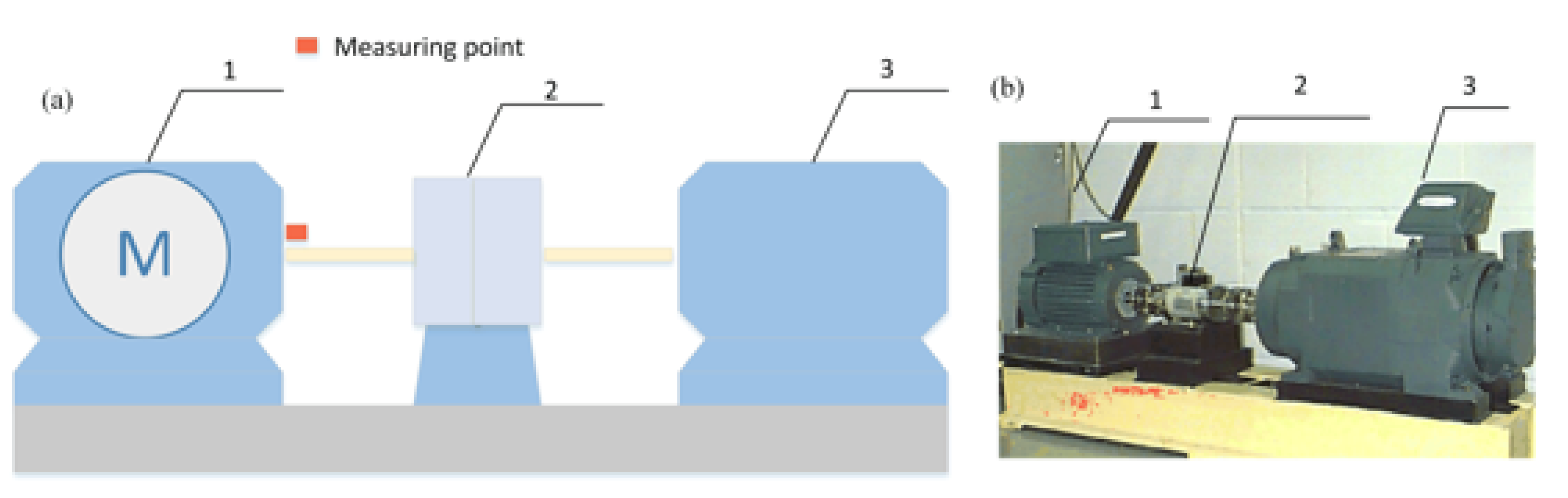

| 6205-2RS JEM SKF (Diameter/Inch) | |||||
|---|---|---|---|---|---|
| Ball Number | Contact Angle | Ball Diameter | Outside Diameter | Inside Diameter | Pitch Diameter |
| 9 | 0 | 0.3126 | 2.0472 | 0.9843 | 1.537 |
| Fault Category | Fault Diameter | Label of Classification | Fault Category | Fault Diameter | Label of Classification |
|---|---|---|---|---|---|
| Ball Fault 1 | 0.007 | 1 | Inner Race 3 | 0.021 | 7 |
| Ball Fault 2 | 0.014 | 2 | Inner Race 4 | 0.028 | 8 |
| Ball Fault 3 | 0.021 | 3 | Normal | 0 | 9 |
| Ball Fault 4 | 0.028 | 4 | Outer Race 1 | 0.007 | 10 |
| Inner Race 1 | 0.007 | 5 | Outer Race 2 | 0.014 | 11 |
| Inner Race 2 | 0.014 | 6 | Outer Race 3 | 0.021 | 12 |
| Input Layer | Hidden Layer | Output Layer |
|---|---|---|
| 12 | 10 | 12 |
| Methods | Average Recognition Rate | Standard Deviation of Recognition Rate | Average Training Time | Average Testing Time |
|---|---|---|---|---|
| MPE | 92.58% | 0.03170 | 0.3011 s | 1.0048 s |
| Improved MPE | 96.25% | 0.02990 | 0.2917 s | 0.9438 s |
| EMD-Improved MPE | 93.36% | 0.03210 | 0.3068 s | 1.0203 s |
| EEMD-Improved MPE | 95.56% | 0.03540 | 0.3100 s | 1.0998 s |
| IF-Improved MPE | 95.70% | 0.03490 | 0.3198 s | 1.0902 s |
| LMD-Improved MPE | 91.57% | 0.03399 | 0.3145 s | 1.1282 s |
| K- ALIF- Improved MPE | 99.98% | 0.00079 | 0.2913 s | 0.9213 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lv, Y.; Ge, M. A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy. Entropy 2021, 23, 191. https://doi.org/10.3390/e23020191
Zhang Y, Lv Y, Ge M. A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy. Entropy. 2021; 23(2):191. https://doi.org/10.3390/e23020191
Chicago/Turabian StyleZhang, Yi, Yong Lv, and Mao Ge. 2021. "A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy" Entropy 23, no. 2: 191. https://doi.org/10.3390/e23020191
APA StyleZhang, Y., Lv, Y., & Ge, M. (2021). A Rolling Bearing Fault Classification Scheme Based on k-Optimized Adaptive Local Iterative Filtering and Improved Multiscale Permutation Entropy. Entropy, 23(2), 191. https://doi.org/10.3390/e23020191







