The Role of Entropy in Construct Specification Equations (CSE) to Improve the Validity of Memory Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Memory Tests and Sample
2.2. Human-Based Measures
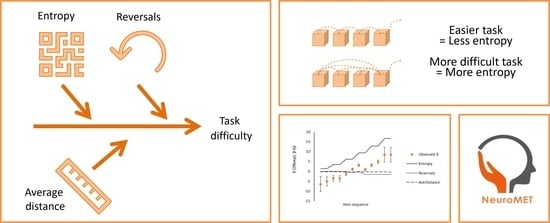
2.3. Entropy and Item Response Models
2.4. Entropy and Construct Specification Equations
3. Results
3.1. Case Study: Block Tapping Recall—Corsi Block Test
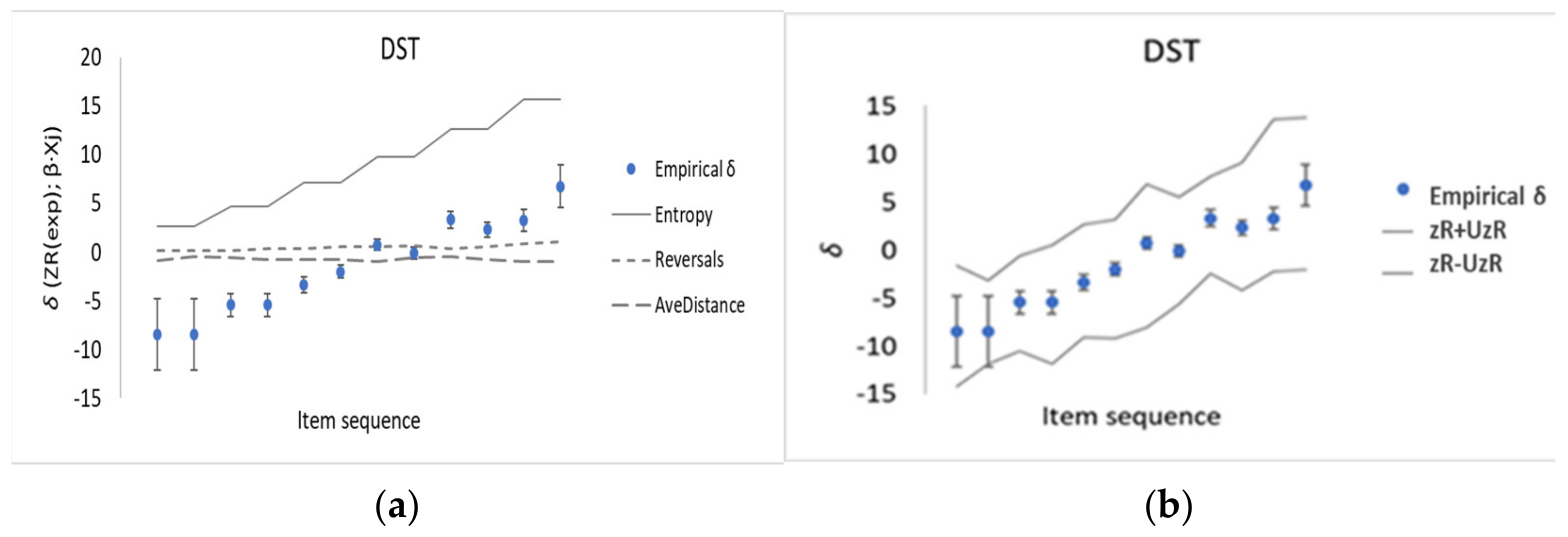
3.2. Case Study: Digit Recall—Digital Span Test
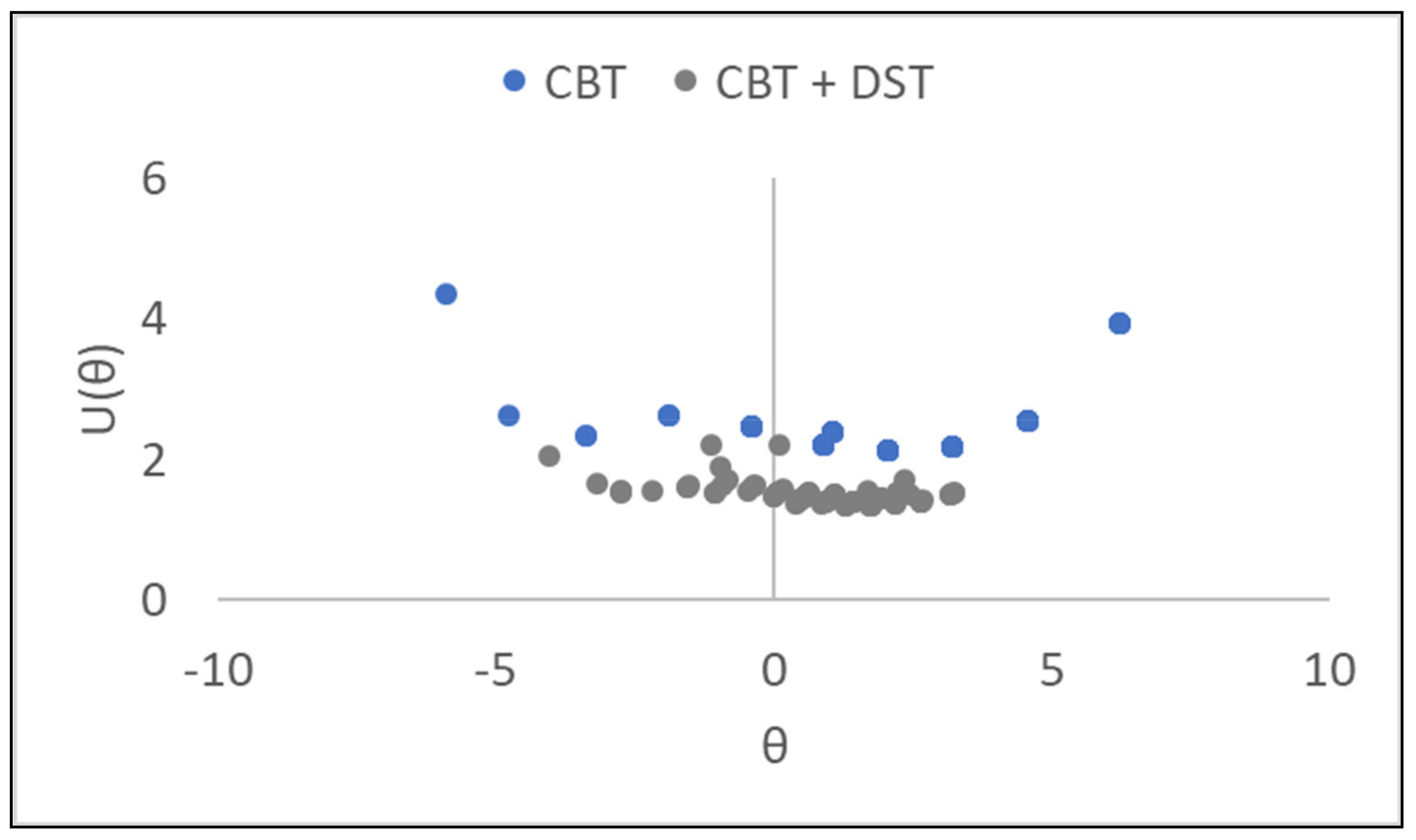
3.3. Contrasting CSEs from Knox Cube Test, Corsi Block Test, and Digit Span Test
3.4. Combination of Memory Items from Corsi Block Test and Digit Span Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Brain Council. Driving Policy to Optimise Care for People with Alzheimer’s Disease in Europe Today and Tomorrow; European Brain Council: Brussels, Belgium, 2018. [Google Scholar]
- Hobart, J.; Cano, S.J.; Posner, H.; Selnes, O.; Stern, Y.; Thomas, R.; Zajicek, J.; Initiative, A.D.N. Putting the Alzheimer’s Cognitive Test to the Test II: Rasch Measurement Theory. Alzheimer’s Dement. 2013, 9, S10–S20. [Google Scholar] [CrossRef]
- Hobart, J.; Cano, S.J.; Posner, H.; Selnes, O.; Stern, Y.; Thomas, R.; Zajicek, J.; Initiative, A.D.N. Putting the Alzheimer’s Cognitive Test to the Test I: Traditional Psychometric Methods. Alzheimer’s Dement. 2012, 9, S4–S9. [Google Scholar] [CrossRef] [PubMed]
- Cano, S.J.; Pendrill, L.R.; Barbic, S.P.; Fisher, W.P. Patient-Centred Outcome Metrology for Healthcare Decision-Making. J. Phys. Conf. Ser. 2018, 1044, 012057. [Google Scholar] [CrossRef]
- Pendrill, L. Assuring Measurement Quality in Person-Centred Healthcare. Meas. Sci. Technol. 2018, 29, 034003. [Google Scholar] [CrossRef]
- Rossi, G.B. Measurement and Probability A Probabilistic Theory of Measurement with Applications; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Pendrill, L.R. Man as a Measurement Instrument. NCSLI Meas. 2014, 9, 24–35. [Google Scholar] [CrossRef]
- Pendrill, L.; Melin, J.; Cano, S.J.; The EMPIR NeuroMET 15HLT04 Consortium. Metrological References for Health Care Based on Entropy. In Proceedings of the 19th International Congress of Metrology (CIM2019), Paris, France, 24–26 September 2019. [Google Scholar] [CrossRef]
- Thurstone, L.L. The Stimulus-Response Fallacy in Psychology. Psychol. Rev. 1923, 30, 354–369. [Google Scholar] [CrossRef]
- Stenner, A.J.; Smith, M. Testing Construct Theories. Percept. Mot. Ski. 1982, 55, 415–426. [Google Scholar] [CrossRef]
- Michell, J. Quantitative Science and the Definition of Measurement in Psychology. Br. J. Psychol. 1997, 88, 355–383. [Google Scholar] [CrossRef]
- Pendrill, L. Quality Assured Measurement: Unification across Social and Physical Sciences; Springer Series in Measurement Science and Technology; Springer Nature Switzerland AG: Cham, Switzerland, 2019. [Google Scholar]
- Carnot, L. Principes Fondamentaux de L’éQuilibre et du Mouvement; Par, L.N.M. Carnot; De L’Imprimerie de Crapelet. A Paris, chez Deterville, Libraire, Rue du Battoir, no 16, Quartier S. André-des-Arcs. An XI-1803; Chez Deterville: Paris, France, 1803. [Google Scholar]
- Maroney, O. Information Processing and Thermodynamic Entropy. In Stanford Encyclopedia of Philosophy; Zalta, E., Ed.; Fall 2009; The Metaphysics Research Lab, Center for the Study of Language and Information (CSLI), Stanford University: Stanford, CA, USA, 2009; ISSN 1095-5054. [Google Scholar]
- Wikipedia. Entropy in Thermodynamics and Information Theory. Available online: https://en.wikipedia.org/wiki/Entropy_in_thermodynamics_and_information_theory. (accessed on 31 January 2021).
- Weaver, W.; Shannon, C. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1963. [Google Scholar]
- Liu, X.; Fu, Z. A Novel Recognition Strategy for Epilepsy EEG Signals Based on Conditional Entropy of Ordinal Patterns. Entropy 2020, 22, 1092. [Google Scholar] [CrossRef]
- Wolins, L.; Wright, B.D.; Rasch, G. Probabilistic Models for some Intelligence and Attainment Tests. J. Am. Stat. Assoc. 1982, 77, 220. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory, Physics Today, 2nd ed.; Academic Press: Cambridge, MA, USA, 1962. [Google Scholar]
- Melin, J.; Pendrill, L. The Role of Construct Specification Equations (CSE) and Entropy in the Measurement of Memory. In Person Centered Outcome Metrology; Cano, S.J., Ed.; Springer: New York, NY, USA, 2020. [Google Scholar]
- Stenner, A.J.; Burdick, H.E.; Sanford, E.; Burdick, D.S. How Accurate Are Lexile Text Measures? J. Appl. Meas. 2006, 7, 307–322. [Google Scholar]
- Corsi, P.M. Human Memory and the Medial Temporal Region of the Brain; Department of Psychology, McGill University: Montreal, QC, Canada, 1973. [Google Scholar]
- Wechsler, D. Wechsler Adult Intelligence Scale; Pearson: London, UK, 1955. [Google Scholar]
- EMPIR 15HLT04 NeuroMET. Innovative Measurements for Improved Diagnosis and Management of Neurodegenerative Diseases. Available online: https://www.lgcgroup.com/our-programmes/empir-neuromet/neuromet/ (accessed on 1 December 2020).
- Wallin, A.; Nordlund, A.; Jonsson, M.; Lind, K.; Edman, Å.; Göthlin, M.; Stålhammar, J.; Eckerström, M.; Kern, S.; Börjesson, A.-H.; et al. The Gothenburg MCI Study: Design and Distribution of Alzheimer’s Disease and Subcortical Vascular Disease Diagnoses from Baseline to 6-Year Follow-Up. Br. J. Pharmacol. 2015, 36, 114–131. [Google Scholar] [CrossRef]
- Cano, S.J.; Hobart, J.C. The Problem with Health Measurement. Patient Prefer. Adherence 2011, 5, 279–290. [Google Scholar] [CrossRef]
- Mosteller, F.; Tukey, J.W. Data Analysis and Regression: A Second Course in Statistics; Addison-Wesley Publishing Company: Boston, MA, USA, 1977. [Google Scholar]
- Tukey, J.W. Data Analysis and Behavioural Science. In The Collected Works of John a Tukey, Volume III, Philosophy and Principles of Data Analysis 1949–1964; University North Carolina: Chapel Hill, NC, USA, 1986. [Google Scholar]
- Pearson, K. Mathematical Contributions to the Theory of Evolution—On a Form of Spurious Correlation Which May Arise When Indices Are Used in the Measurement of Organs; The Royal Society: London, UK, 1897; Volume 60, pp. 489–498. [Google Scholar]
- Pendrill, L.; Melin, J. Assuring Measurement Quality in Person-Centred Care in Person Centered Outcome Metrology; Cano, S.J., Ed.; Springer: New York, NY, USA, 2020. [Google Scholar]
- Stenner, A.J.; Smith, M.; Burdick, D.S. Toward a Theory of Construct Definition. J. Educ. Meas. 1983, 20, 305–316. [Google Scholar] [CrossRef]
- Bissell, D.; Montgomery, D.C. Introduction to Statistical Quality Control. J. R. Stat. Soc. Ser. D Stat. 1986, 35, 81. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 2007, 22, 79–86. [Google Scholar] [CrossRef]
- Chesaniuk, M. Chapter 19: Logistic and Poisson Regression. Available online: https://ademos.people.uic.edu/Chapter19.html (accessed on 1 November 2020).
- Mayne, A.J.; Klir, G.J.; Folger, T.A. Fuzzy Sets, Uncertainty, and Information. J. Oper. Res. Soc. 1990, 41, 884. [Google Scholar] [CrossRef]
- Schneider, T.D.; Stormo, G.D.; Gold, L.; Ehrenfeucht, A. Information Content of Binding Sites on Nucleotide Sequences. J. Mol. Biol. 1986, 188, 415–431. [Google Scholar] [CrossRef]
- Passolo, A. Measurement, in Advanced Mathematical and Computational Tools in Metrology and Testing: AMCTM XI; Forbes, A., Ed.; World Scientific Publishing Company: Singapore, 2018; pp. 273–285. [Google Scholar]
- Feynman, R. Richard Feynman’s Blackboard at the Time of His Death. 1988. Available online: http://archives-dc.library.caltech.edu/islandora/object/ct1%3A483 (accessed on 25 October 2020).
- Knox, H.A. A Scale, Based on the Work at Ellis Island, for Estimating Mental Defect. J. Am. Med. Assoc. 1914, LXII, 741. [Google Scholar] [CrossRef]
- Stenner, A.J.; Fisher, J.W.P.; Stone, M.H.; Burdick, D.S. Causal Rasch models. Front. Psychol. 2013, 4, 536. [Google Scholar] [CrossRef]
- Schnore, M.M.; Partington, J.T. Immediate Memory for Visual Patterns: Symmetry and Amount of Information. Psychon. Sci. 1967, 8, 421–422. [Google Scholar] [CrossRef]
- Imbo, I.; Szmalec, A.; Vandierendonck, A. The Role of Structure in Age-Related Increases in Visuo-Spatial Working Memory Span. Psychol. Belg. 2010, 49, 275. [Google Scholar] [CrossRef][Green Version]
- Melin, J.; Pendrill, L.; Cano, S.J.; The EMPIR NeuroMET 15HLT04 Consortium. Towards Patient-Centred Cognition Metrics. J. Phys. Conf. Ser. 2019, 1379, 012029. [Google Scholar] [CrossRef]
- Chekaf, M.; Gauvrit, N.; Guida, A.; Mathy, F. Compression in Working Memory and Its Relationship with Fluid Intelligence. Cogn. Sci. 2018, 42, 904–922. [Google Scholar] [CrossRef] [PubMed]
- Green, K.E.; Smith, R.M. A Comparison of Two Methods of Decomposing Item Difficulties. J. Educ. Stat. 1987, 12, 369–381. [Google Scholar] [CrossRef]
- Yao, Y.; Lu, W.L.; Xu, B.; Li, C.B.; Lin, C.P.; Waxman, D.; Feng, J. The Increase of the Functional Entropy of the Human Brain with Age. Sci. Rep. 2013, 3, 2853. [Google Scholar] [CrossRef]
- Chen, L.; Liang, X.; Li, T. Collaborative Performance Research on Multi-Level Hospital Management Based on Synergy Entropy-HoQ. Entropy 2015, 17, 2409–2431. [Google Scholar] [CrossRef]
- Maršik, F.; Mejsnar, J.; Mejsnar, F.M.J. The Balance of Entropy Underlying Muscle Performance. J. Non Equilib. Thermodyn. 1994, 19, 197. [Google Scholar] [CrossRef]


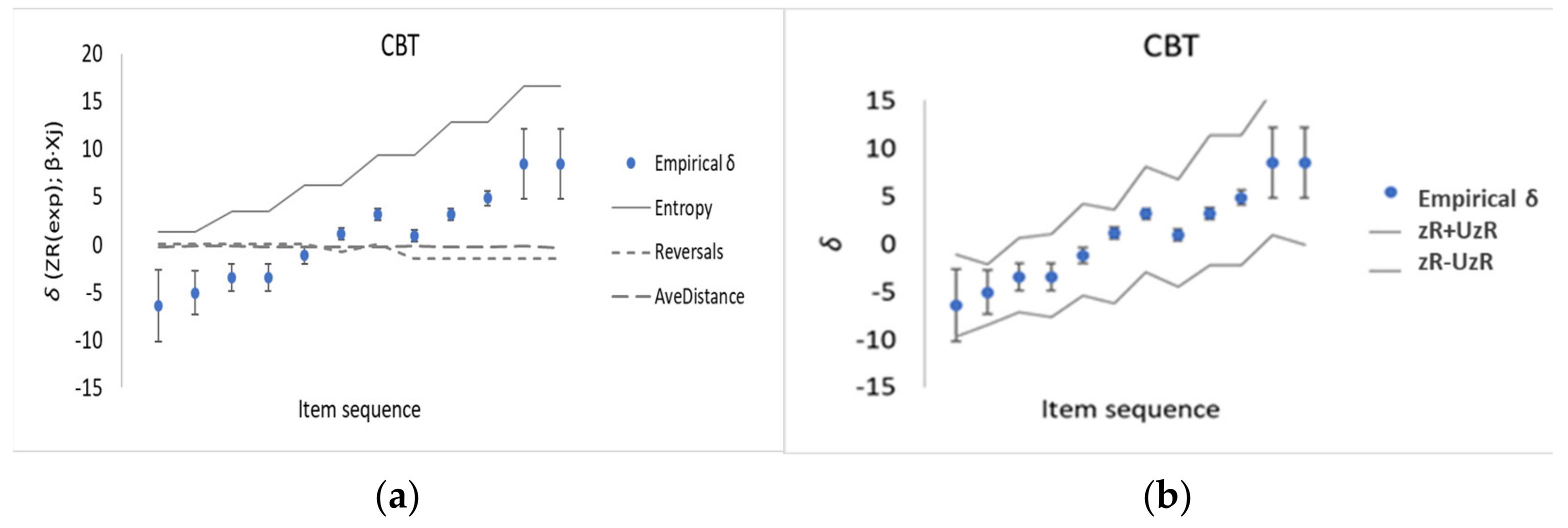

| Tapping Sequence | Empirical Memory Task Difficulty, δ | U(δ) k = 2 | Entropy (Equation (6)) | Reversals | Average Distance |
|---|---|---|---|---|---|
| 2 taps, 1st | −6.5 | 3.8 | 0.69 | 0 | 10.5 |
| 2 taps, 2nd | −5.1 | 2.3 | 0.69 | 0 | 4.7 |
| 3 taps, 1st | −3.5 | 1.5 | 1.79 | 0 | 7.7 |
| 3 taps, 2nd | −3.5 | 1.5 | 1.79 | 0 | 9.9 |
| 4 taps, 1st | −1.2 | 0.8 | 3.18 | 0 | 10.3 |
| 4 taps, 2nd | 1.1 | 0.6 | 3.18 | 1 | 9.9 |
| 5 taps, 1st | 3.1 | 0.6 | 4.79 | 0 | 10.4 |
| 5 taps, 2nd | 0.9 | 0.6 | 4.79 | 2 | 7.5 |
| 6 taps, 1st | 3.1 | 0.6 | 6.58 | 2 | 9.8 |
| 6 taps, 2nd | 4.8 | 0.8 | 6.58 | 2 | 9.7 |
| 7 taps, 1st | 8.5 | 3.7 | 8.53 | 2 | 6.1 |
| 7 taps, 2nd | 8.5 | 3.7 | 8.53 | 2 | 13.3 |
| Number Sequence | Empirical Memory Task Difficulty, δ | U(δ) k = 2 | Entropy Equation (6) | Reversals | Average Distance |
|---|---|---|---|---|---|
| 3 digits, 1st | −8.5 | 3.7 | 1.79 | 1 | 3.7 |
| 3 digits, 2nd | −8.5 | 3.7 | 1.79 | 1 | 2.0 |
| 4 digits, 1st | −5.4 | 1.2 | 3.18 | 1 | 2.5 |
| 4 digits, 2nd | −5.4 | 1.2 | 3.18 | 2 | 3.5 |
| 5 digits, 1st | −3.4 | 0.8 | 4.79 | 2 | 3.2 |
| 5 digits, 2nd | −2.0 | 0.7 | 4.79 | 3 | 3.4 |
| 6 digits, 1st | 0.8 | 0.6 | 6.58 | 3 | 4.3 |
| 6 digits, 2nd | −0.1 | 0.6 | 6.58 | 4 | 2.7 |
| 7 digits, 1st | 3.3 | 0.9 | 8.53 | 2 | 2.1 |
| 7 digits, 2nd | 2.3 | 0.8 | 8.53 | 3 | 3.6 |
| 8 digits, 1st | 3.3 | 1.1 | 10.60 | 5 | 4.4 |
| 8 digits, 2nd | 6.8 | 2.2 | 10.60 | 6 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melin, J.; Cano, S.; Pendrill, L. The Role of Entropy in Construct Specification Equations (CSE) to Improve the Validity of Memory Tests. Entropy 2021, 23, 212. https://doi.org/10.3390/e23020212
Melin J, Cano S, Pendrill L. The Role of Entropy in Construct Specification Equations (CSE) to Improve the Validity of Memory Tests. Entropy. 2021; 23(2):212. https://doi.org/10.3390/e23020212
Chicago/Turabian StyleMelin, Jeanette, Stefan Cano, and Leslie Pendrill. 2021. "The Role of Entropy in Construct Specification Equations (CSE) to Improve the Validity of Memory Tests" Entropy 23, no. 2: 212. https://doi.org/10.3390/e23020212
APA StyleMelin, J., Cano, S., & Pendrill, L. (2021). The Role of Entropy in Construct Specification Equations (CSE) to Improve the Validity of Memory Tests. Entropy, 23(2), 212. https://doi.org/10.3390/e23020212