Non-Invertible Public Key Certificates
Abstract
:1. Introduction
- 1.
- Multiplication-based protocol. In a ring with unity over where and p, q are prime numbers. An integer may or may not have a multiplicative inverse. Multiplication between invertible and a non-invertible integer yields a non-invertible integer according to the basic properties of modular arithmetic. Alice multiplies a random non-invertible by a random invertible , then she sends the result to Bob who multiplies it by his random invertible returning the resulting integer to Alice who removes multiplying by and sending the result to Bob. Finally, Bob removes his invertible integer applying . At this point Bob has obtained . Although a non-invertible integer does not have a multiplicative inverse, hence factorization of the public integers are prohibited, a division attack is discussed in [5].
- 2.
- Exponent-based protocol. The integer that results after exponentiation say gives a non-invertible integer. Using this math property, the protocol defines that Alice sends to Bob who returns to her. Then she multiplies it by and sends back . Bob applies thus obtaining the shared secret . Unfortunately, this version of the protocol is also vulnerable to a division attack [5].
- 3.
- Non-invertible KEP. This protocol defines a public key exchange algorithm. To surpass the division attack, ni-KEP introduces Euler’s identity to derive the keys which are defined according to the relations , for Alice’s and Bob’s public keys respectively and n is obtained as where p and q are small prime public numbers and r is a big prime public integer. On the other hand, constitute the private key, while the number is derived from the equation where is the Euler’s totient equation. A detailed discussion of this protocol will be presented in a later section.
2. Cryptography in the Quantum Era
3. Public Key Cryptography
3.1. Digital Certificates
3.2. Certification Authority (CA)
- 1.
- Alice obtains the certificate of CA signed by CA. Since Alice has the public key of CA, she can get the public key of CA from its certificate and verify it using the signature of CA on the certificate.
- 2.
- From the directory, Alice obtains the certificate of Bob signed by CA. Since Alice now has the public key of CA, she can verify the signature, therefore getting Bob’s public key.
4. Lizama’s Key Exchange Protocol
- 1.
- Once public keys have been exchanged, Alice and Bob perform two operations over the numbers received: exponentiation and multiplication as indicated in Table 1.
- 2.
- To derive the results in the right column of Table 1, Euler’s theorem is applied in . The theorem is written in Equation (1) where r is an integer safe prime. As a result that , we have that . Here, k and n are relative prime to each other, so k is an invertible integer in . The exponent constitutes the private key, is chosen randomly, but and sum up , thus according to Equation (1) we have because k is an invertible integer in .
- 3.
- Users exchange the resulting value , which is multiplied by the corresponding inverse at each side to derive the secret shared key as depicted in Figure 4.

- —
- —
- if and , we have , then yields and .
- —
- since the private key is conformed by x and k, its size is computed as which gives 1536.
4.1. Cipher-System
4.2. Mathematical Representation
5. Key Certification with Lizama’s ni-KEP
- 1.
- To certify their public key with the Certification Authority CA, user i sends to CA their public key .
- 2.
- If CA approves the request of i, they generate and publish the certified key which has been derived according to Table 3.
- 3.
- The CA’s public database of certified keys can be seen in Table 4 which contains the certified keys of Alice and Bob.
- 1.
- Using CA’s public key , Alice computes . In addition, she computes using Bob’s public key .
- 3.
- Alice multiplies them by Bob’s certified key and sends the resulting integer number to Bob. The same procedure is applied by him.
- 4.
- Bob multiplies the received integer by twice, thus he obtains the secret shared key (see Figure 5).
- 5.
- Applying this procedure, Bob derives the same secret number .

5.1. Indistinguishability
5.2. Multiple CAs
- 1.
- Using CA’s public key , Alice computes , she also computes with Bob’s public key .
- 3.
- Alice multiplies them by Bob’s certificate and CA’s certificate and sends the resulting integer number to Bob. The same procedure is applied by Bob.
- 4.
- Alice multiplies the received integer by twice, thus she obtains the secret shared key (see Figure 6).
- 5.
- Applying the same procedure, Bob derives the secret shared number .
| CA | User | Public Key | Certified Key |
|---|---|---|---|
| CA | - | ||
| CA | |||
| CA | Alice | ||
| CA | - | ||
| CA | |||
| CA | Bob |
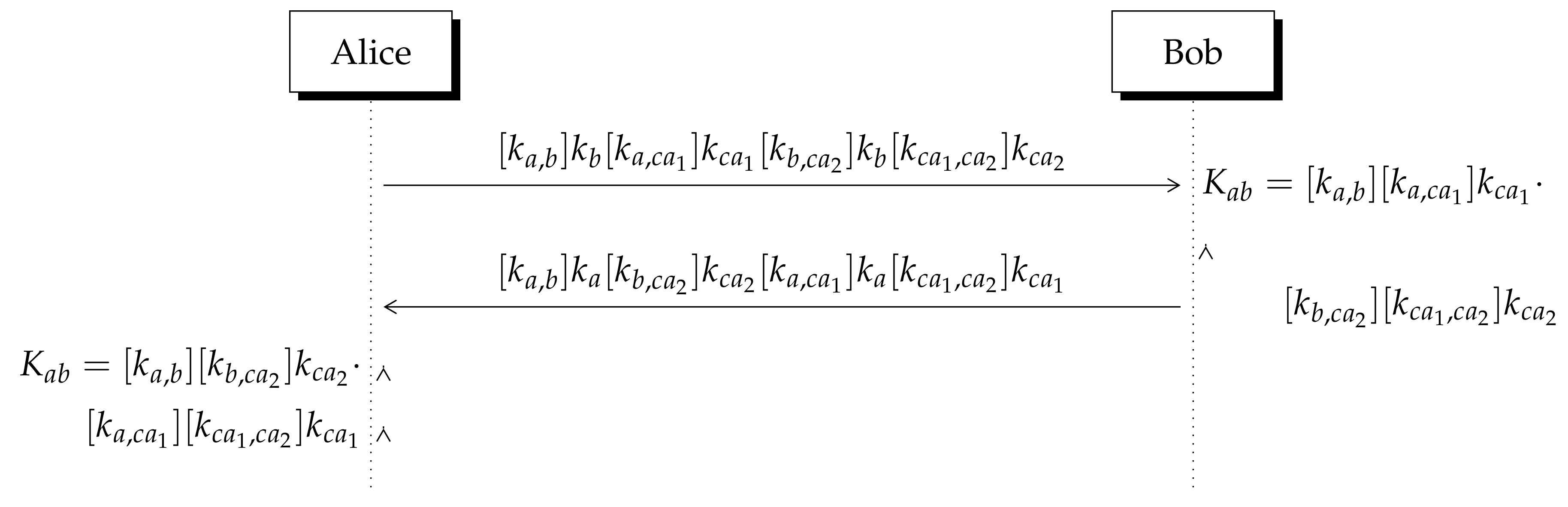
6. Perfect Forward Secrecy (PFS)
- 1.
- Alice and Bob share a certified key from a previous exchange.
- 2.
- Using CA’s public key , Alice computes . In addition, according to Table 6, Alice computes using Bob’s public key .
- 4.
- Alice multiplies them by Bob’s certificate and sends the resulting number to Bob. The same procedure is applied by Bob.
- 5.
- Bob multiplies the received integer by , thus he obtains the secret shared key (see Figure 7).
- 6.
- Conversely, Alice multiplies the received integer by , thus she gets the secret shared key .
| Short Notation | Mathematical Operation |
|---|---|
| , | |

7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. RSA Cryptosystem
Appendix A.2. Diffie–Hellman Key Exchange
Appendix A.3. Prefix Attack
Appendix A.4. Multiplication-Based Attack
- ,
- because
- ,
- where
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994. [Google Scholar]
- Barreno, M.A. The Future of Cryptography under Quantum Computers. Dartmouth College Undergraduate Theses, 23 July 2002. Available online: https://digitalcommons.dartmouth.edu/senior_theses/23 (accessed on 11 February 2021).
- Laboratory, I.T. PQC Standardization Process: Third Round Candidate Announcement. Available online: https://csrc.nist.gov/news/2020/pqc-third-round-candidate-announcement (accessed on 11 February 2021).
- Chen, L.; Jordan, S.; Liu, Y.-K.; Moody, D.; Peralta, R.; Perlner, R.; Smith-Tone, D. Report on Post-Quantum Cryptography. Available online: http://cm.1-s.es/2017/nistir_8105_draft.pdf (accessed on 11 February 2021).
- Lizama-Perez, L.A. Non-Invertible Key Exchange Protocol. SN Appl. Sci. 2020, 2, 1–13. Available online: https://link.springer.com/content/pdf/10.1007/s42452-020-2791-3.pdf (accessed on 11 February 2021). [CrossRef]
- Grover, L.K. A Fast Quantum Mechanical Algorithm for Database Search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar]
- Bennett Ch, H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. arXiv 2020, arXiv:2003.06557. [Google Scholar] [CrossRef]
- Lizama-Pérez, L.A.; López, J.M.; De Carlos-López, E.; Venegas-Andraca, S.E. Quantum flows for secret key distribution in the presence of the photon number splitting attack. Entropy 2014, 16, 3121–3135. [Google Scholar] [CrossRef] [Green Version]
- Lizama-Pérez, L.A.; López, J.M.; De Carlos López, E. Quantum key distribution in the presence of the intercept-resend with faked states attack. Entropy 2017, 19, 4. [Google Scholar] [CrossRef] [Green Version]
- Lizama-Perez, L.A.; López, J.M. Quantum key distillation using binary frames. Symmetry 2020, 12, 1053. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhu, Y.; Ma, D.; Feng, R. Lattice-based key exchange on small integer solution problem. Sci. China Inf. Sci. 2014, 57, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Mao, S.; Zhang, P.; Wang, H.; Zhang, H.; Wu, W. Cryptanalysis of a lattice based key exchange protocol. Perspect. Sci. 2016, 8, 228–230. [Google Scholar] [CrossRef]
- Jao, D.; De Feo, L. Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In Post-Quantum Cryptography. PQCrypto 2011; Lecture Notes in Computer Science; Yang, B.Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Costello, C.; Longa, P.; Naehrig, M. Efficient algorithms for supersingular isogeny diffie-hellman. In Advances in Cryptology—CRYPTO 2016. CRYPTO 2016; Lecture Notes in Computer Science; Robshaw, M., Katz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Matsumoto, T.; Imai, H. Public quadratic polynomial-tuples for efficient signature-verification and message-encryption. In Advances in Cryptology—EUROCRYPT ’88. EUROCRYPT 1988; Lecture Notes in Computer Science; Barstow, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Merkle, R.C. Method of Providing Digital Signatures. US Patent 4,309,569, 5 January 1982. [Google Scholar]
- Lizama-Perez, L.A. Digital signatures over hash-entangled chains. SN Appl. Sci. 2019, 1, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Lizama-Pérez, L.A.; Montiel-Arrieta, L.J.; Hernández-Mendoza, F.S.; Lizama-Servín, L.A.; Eric, S.-A. Public hash signature for mobile network devices. Ing. Investig. Tecnol. 2019, 20, 1–10. Available online: https://pdfs.semanticscholar.org/fce5/99b5af03457e4b94e123e575d1daca8e24ab.pdf (accessed on 11 February 2021).
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V.S. Use of elliptic curves in cryptography. In Advances in Cryptology—CRYPTO ’85 Proceedings. CRYPTO 1985. Lecture Notes in Computer Science; Williams, H.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Bindel, N.; Herath, U.; McKague, M.; Stebila, D. Transitioning to a quantum-resistant public key infrastructure. In Post-Quantum Cryptography. PQCrypto 2017; Lecture Notes in Computer Science; Lange, T., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Pradel, G.; Mitchell, C.J. Post-quantum certificates for electronic travel documents. In Computer Security. ESORICS 2020; Lecture Notes in Computer Science; Boureanu, I., Ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Kampanakis, P.; Panburana, P.; Daw, E.; Van Geest, D. The viability of post-quantum X.509 certificates. IACR Cryptol. ePrint Arch. 2018, 2018, 63. [Google Scholar]
- Polk, W.; Housley, R.; Bassham, L. Algorithms and identifiers for the internet X.509 public key infrastructure certificate and certificate revocation list (crl) profile. Algorithms 2002, 2, 26. [Google Scholar]
- Gerck, E. Overview of Certification Systems: X.509, ca, pgp and Skip. Available online: https://www.blackhat.com/presentations/bh-usa-99/EdGerck/certover.pdf (accessed on 11 February 2021).
- Abdul-Rahman, A. The Pgp Trust Model. EDI Forum J. Electron. Commer. 1997, 10, 27–31. Available online: https://ldlus.org/college/WOT/The_PGP_Trust_Model.pdf (accessed on 11 February 2021).
- NIST Round 3 Finalists. Available online: https://pqc-wiki.fau.edu/w/Special:DatabaseHome (accessed on 11 February 2021).
- Banerjee, U.; Chandrakasan, A.P. Efficient Post-Quantum TLS Handshakes using Identity-Based Key Exchange from Lattices. In Proceedings of the 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]



| User | Operation | Result |
|---|---|---|
| Alice | ||
| Bob |
| Mode | Mathematical Relation |
|---|---|
| Encryption | |
| Decryption |
| Short Notation | Mathematical Operation |
|---|---|
| , | |
| User | Public Key | Certified Key |
|---|---|---|
| CA | - | |
| Alice | ||
| Bob |
| Scheme | System | Public Key (KB) | Private Key (KB) | Signature (KB) |
|---|---|---|---|---|
| Public Key/ KEM | LIZAMA’S KEP | 0.256–0.512 | 0.192–0.384 | – |
| Classic McEliece | 261,120–1,357,824 | 6492–14,120 | – | |
| CRYSTALS-KYBER | 1.632–3.168 | 0.8–1.568 | – | |
| NTRU-HPS | 0.931–1.230 | 1.235–1.592 | – | |
| SABER | 0.672–1.312 | 1.568–3.040 | – | |
| Signature Algorithms | CRYSTALS-DILITHIUM | 1.312–2.592 | – | 2.420–4.595 |
| FALCON | 0.897–1.793 | – | 0.666–0.280 | |
| Rainbow | 157.8–1885.4 | 101.2–1375.7 | 0.066–0.212 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lizama-Perez, L.A.; López R., J.M. Non-Invertible Public Key Certificates. Entropy 2021, 23, 226. https://doi.org/10.3390/e23020226
Lizama-Perez LA, López R. JM. Non-Invertible Public Key Certificates. Entropy. 2021; 23(2):226. https://doi.org/10.3390/e23020226
Chicago/Turabian StyleLizama-Perez, Luis Adrián, and J. Mauricio López R. 2021. "Non-Invertible Public Key Certificates" Entropy 23, no. 2: 226. https://doi.org/10.3390/e23020226







