Security Analysis of a Color Image Encryption Algorithm Using a Fractional-Order Chaos
Abstract
:1. Introduction
- The existence of an equivalent key. CIEA-FOHS encrypts the image using a pseudo-random sequence generated by fractional-order chaos. However, these sequences are not related to plaintext. Thus, these sequences can be considered as equivalent keys.
- Two-stage permutations can be equivalently simplified to only once. The reason is that the two permutations only change the position of the pixel without changing the value of the pixel.
- The paradigm of the diffusion part is insecure. According to the conclusion of Ref. [43], a class of diffusion encryption using module addition and XOR operations can be cracked with only two special plain images and their corresponding cipher images. Unfortunately, CIEA-FOHS is also the case.
2. The Encryption Algorithm under Study
2.1. Fractional-Order Hyperchaotic System
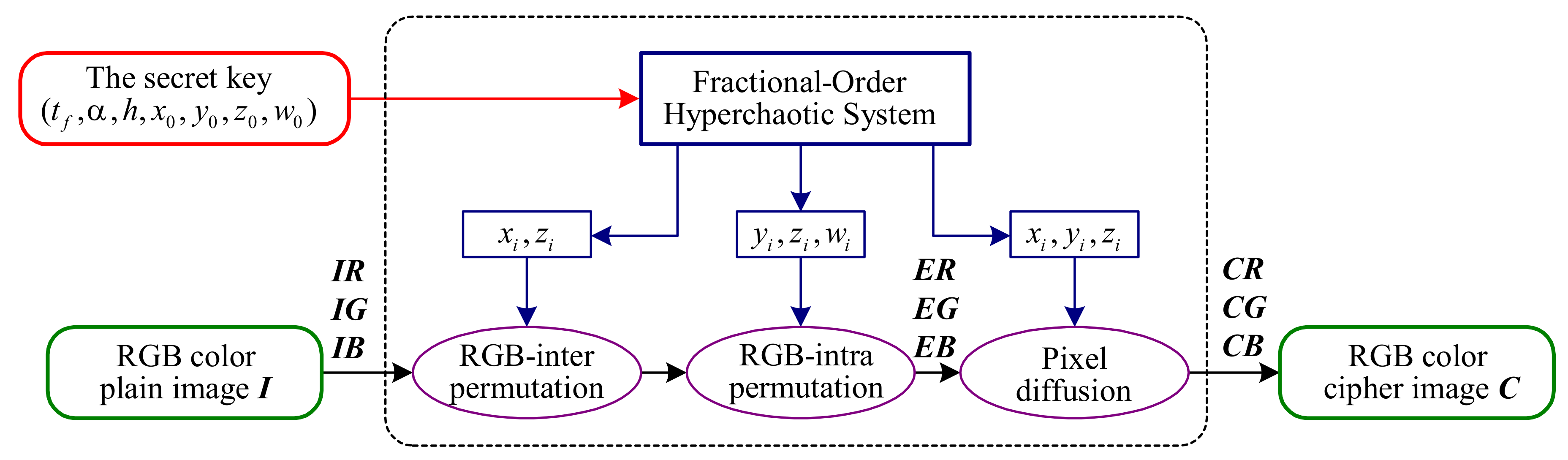
2.2. Description of CIEA-FOHS
- The Secret Key:
- Initialization:
- Stage 1. RGB-inter permutation:
- Stage 2. RGB-intra permutation:
- Stage 3. Pixel diffusion:
3. Security Analysis of CIEA-FOHS
3.1. Preliminary Analysis of CIEA-FOHS
3.2. Analysis on the Diffusion Part
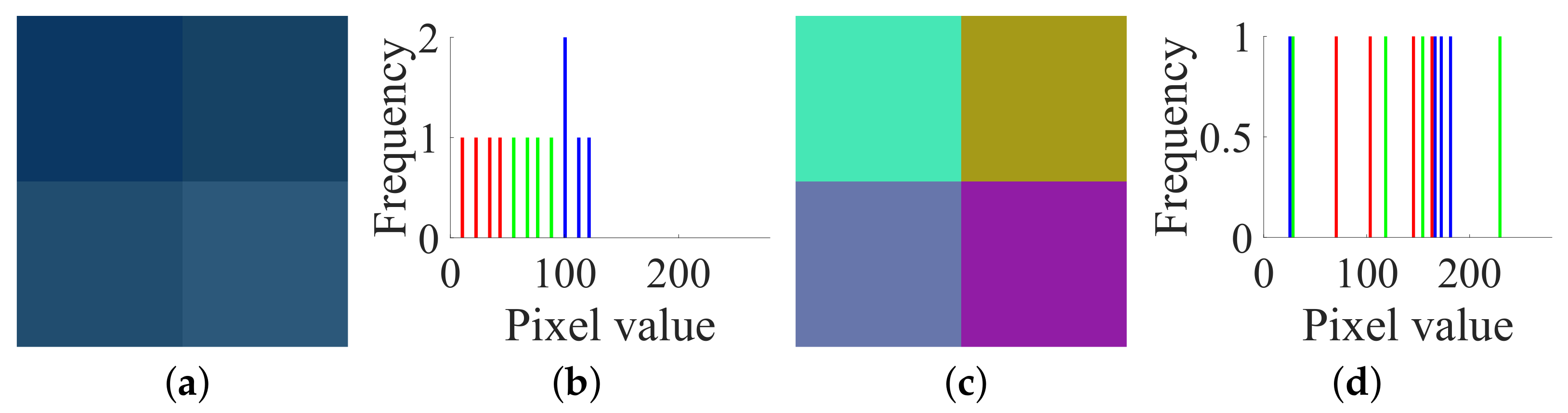
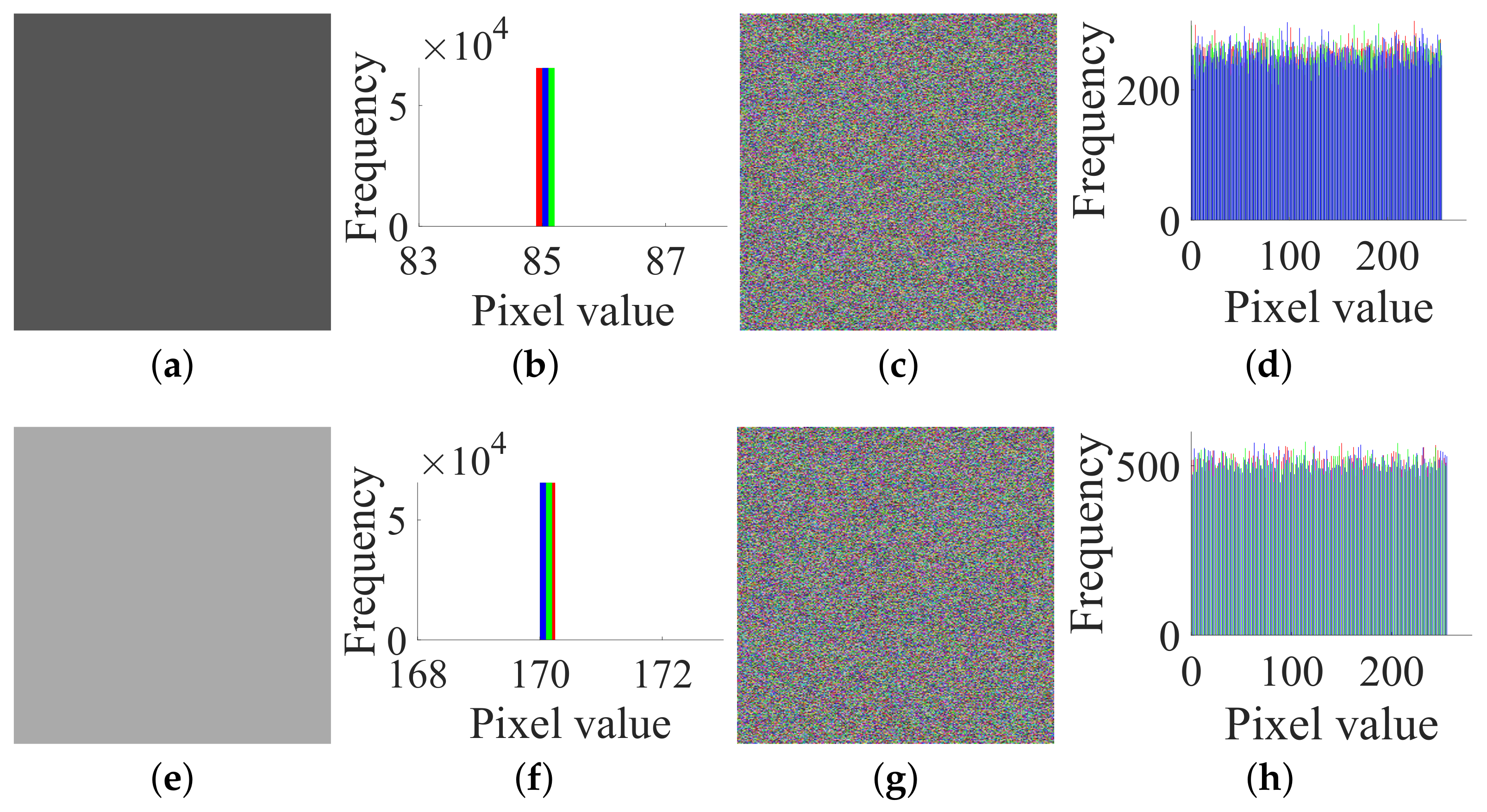
- Step 1. Choose the all-zero plain image and get the corresponding cipher image to determine .
- Step 2. Choose two special plain images and get the corresponding cipher images to determine for .
| Algorithm 1: Determining for |
 |
- Step 3. Eliminate the diffusion part by , , .
3.3. Analysis on the Permutation Part
- Step 1. Choose some special plain images and get their corresponding cipher images to determine the permutation matrix ;
- Step 2. Use the permutation matrix to recover the original images from the permuted images.
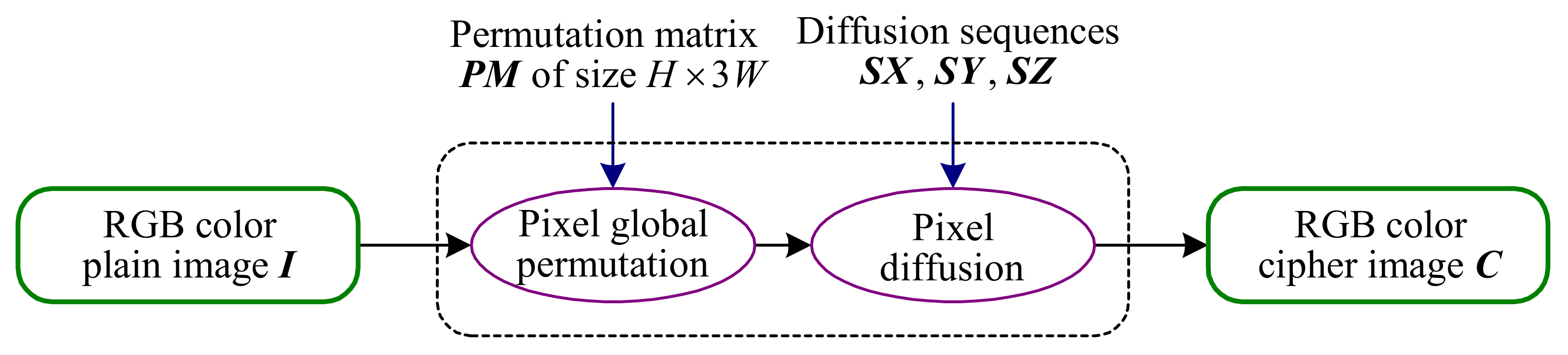
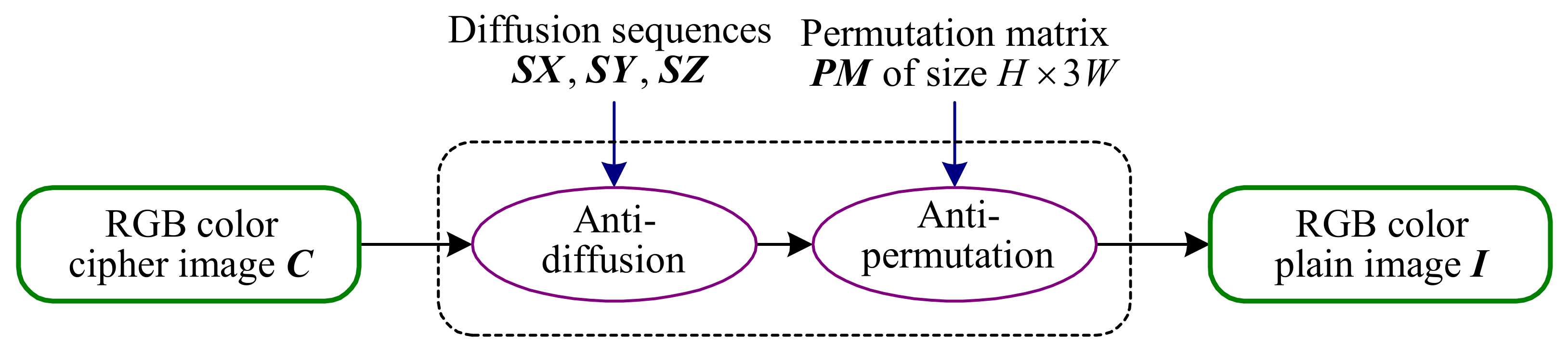
3.4. The Proposed Chosen-Plaintext Attack Method
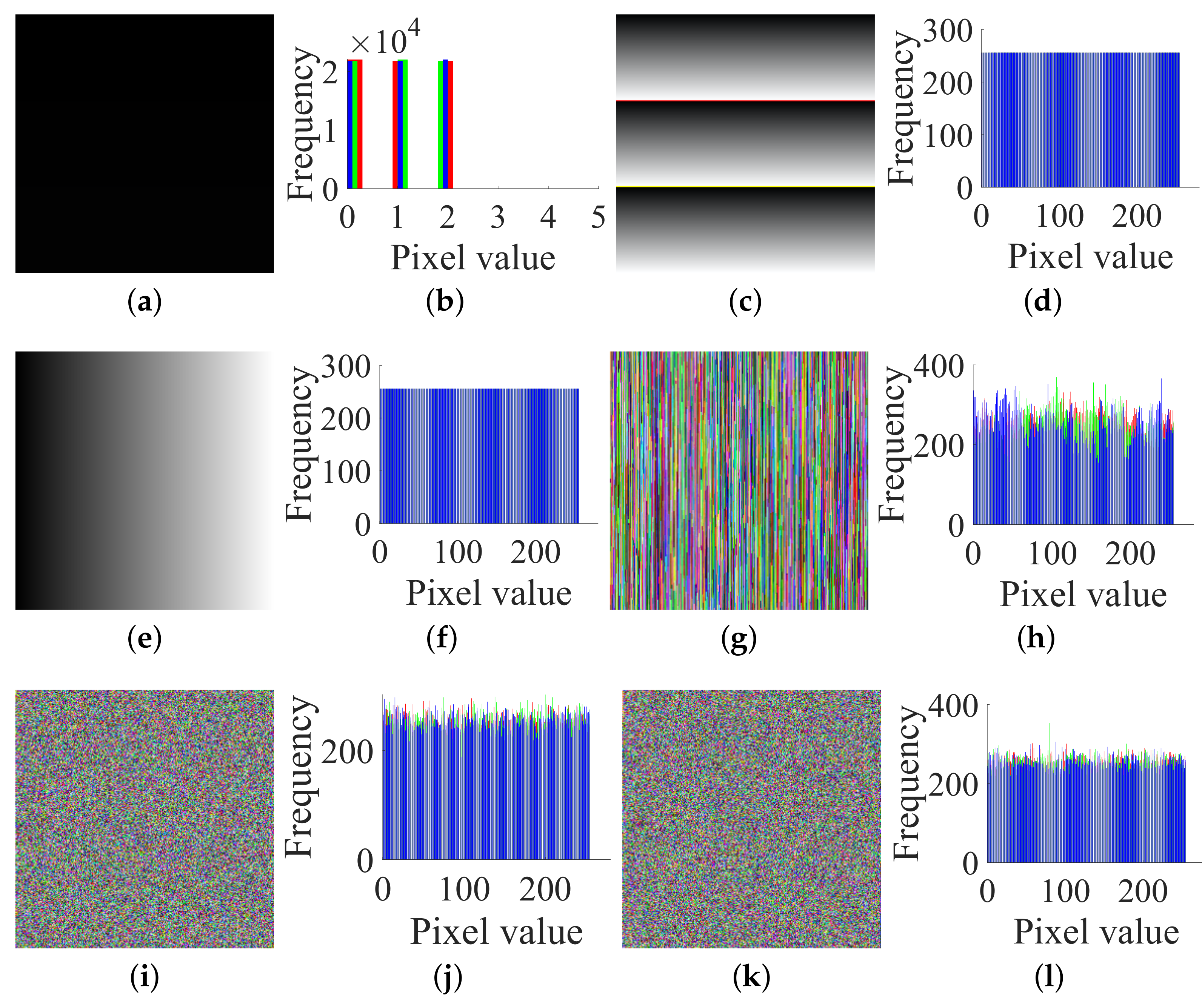
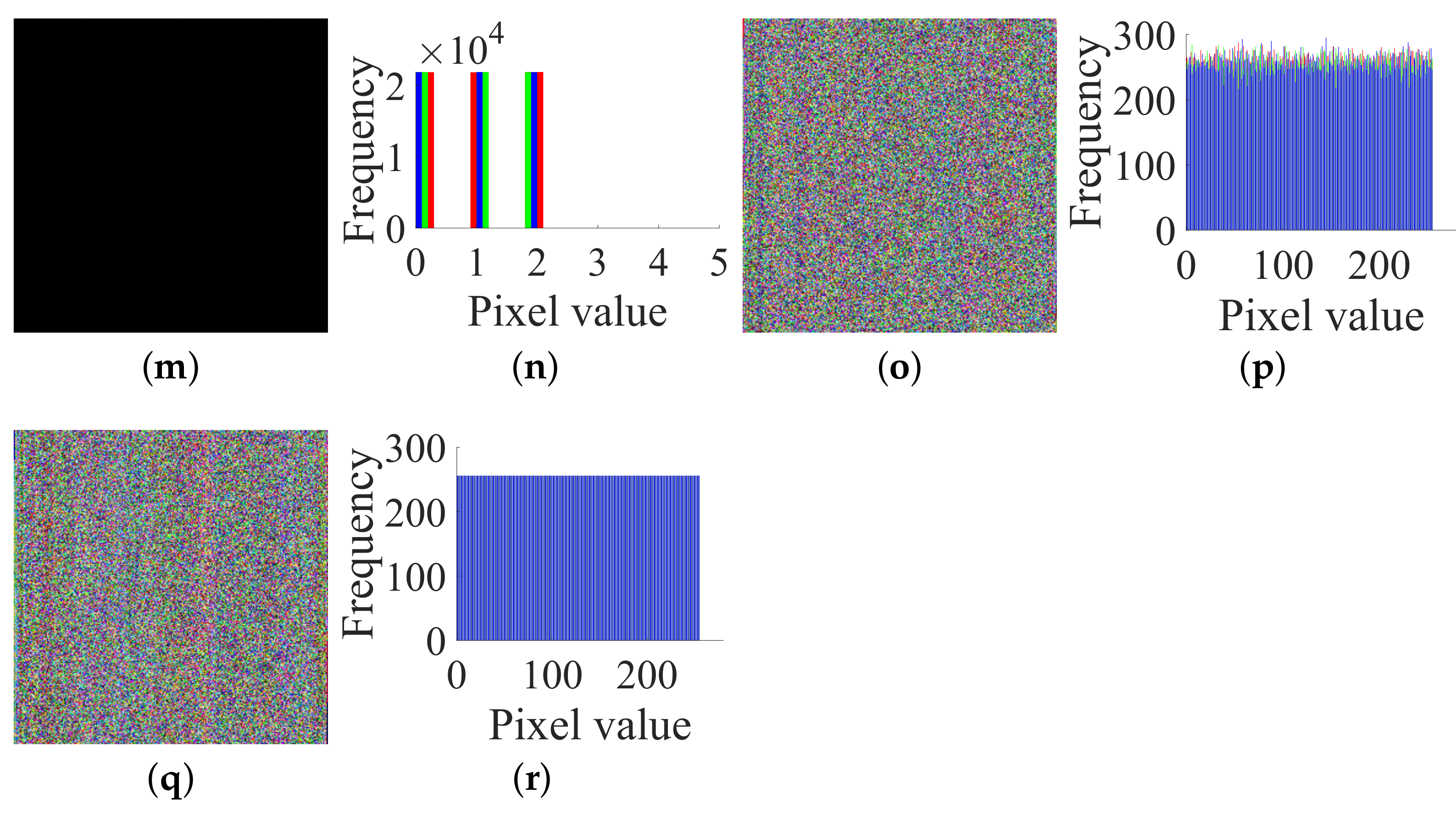
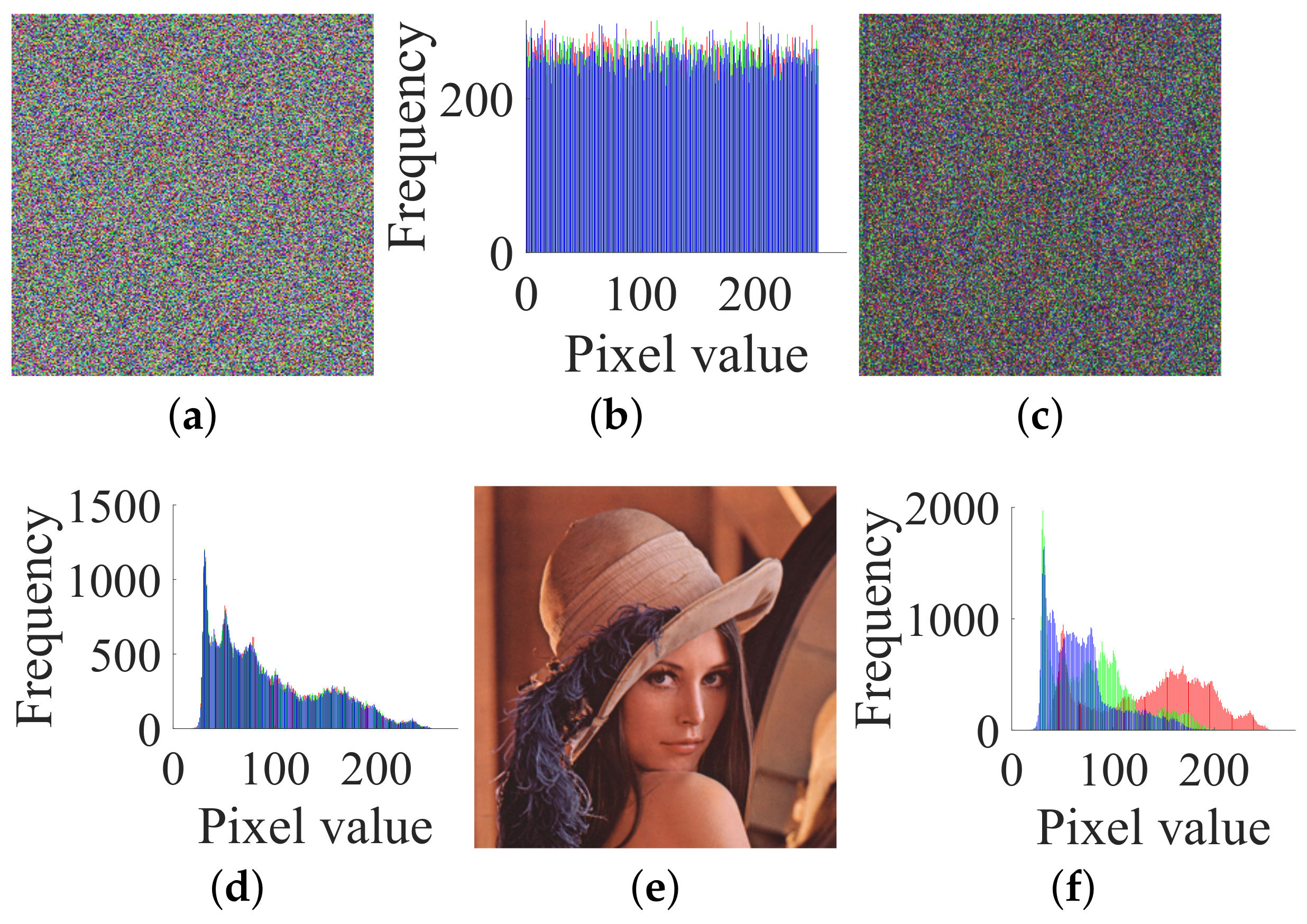
4. Experimental Verifications and Discussions
- Case 1. Breaking CIEA-FOHS with an image of size :
- Case 2. Breaking CIEA-FOHS with “Lenna” of size :
5. Suggestions for Improvement
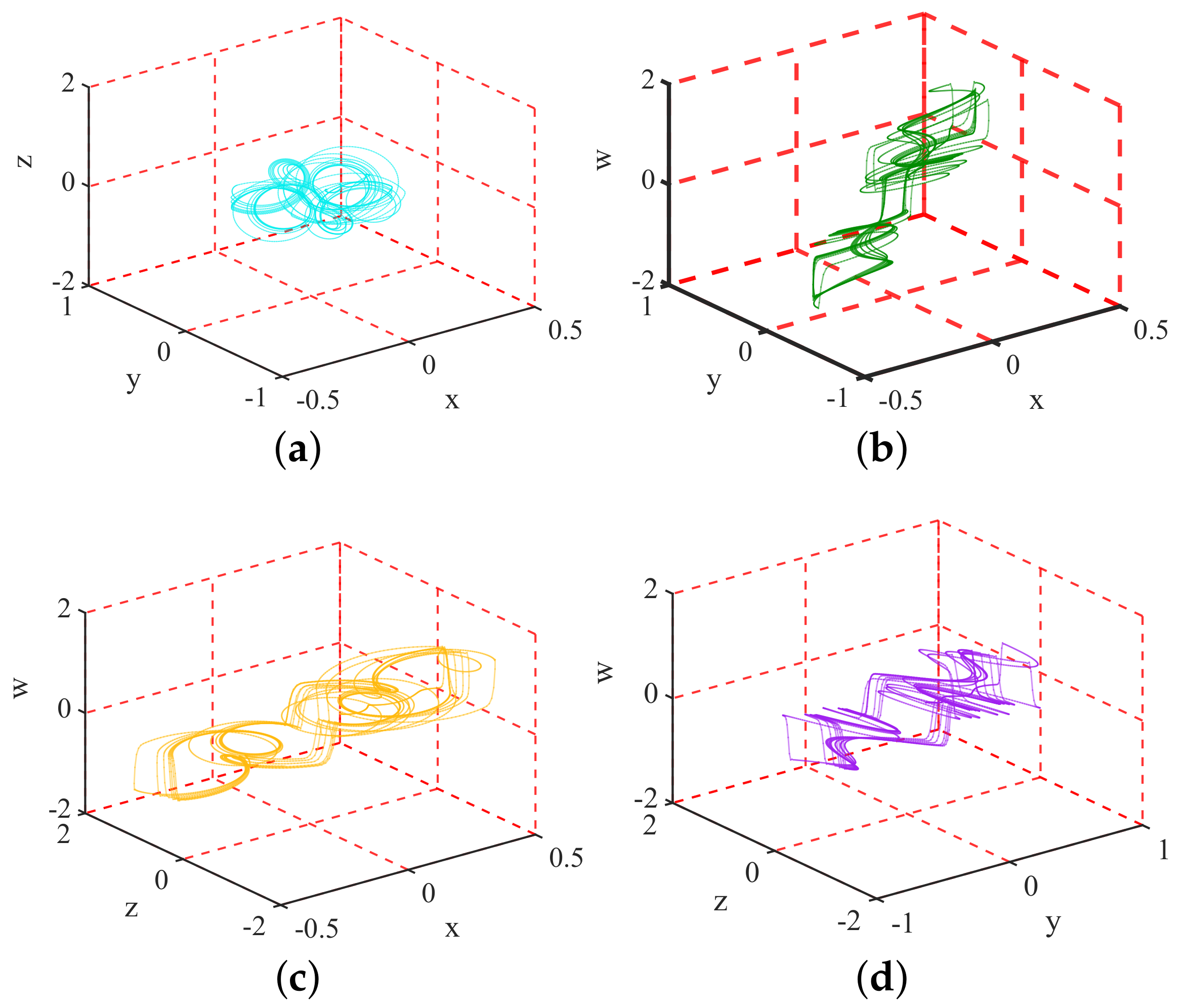
- Suggestion 1. Ensuring the substantial security contribution of the fractional-order chaos to the corresponding cipher. The attractor phase diagram of the fractional-order hyperchaotic system is shown in Figure 1, which shows the extremely complex dynamics. Undoubtedly, fractional-order chaos is one of the preferred sources of entropy for encryption. However, due to the negligence of algorithm design, CIEA-FOHS has serious security defects and is attacked.
- Suggestion 2. Security analysis should be implemented from the perspective of cryptography, not limited to numerical statistical verification. As Ref. [45] points out, many encryption algorithms have excellent statistical analysis results, but they are still insecure. In fact, good statistical analysis results are only a necessary and not a sufficient condition for security. Some security flaws are difficult to reflect with numerical statistical results, but they can be clearly revealed by theoretical security analysis. For example, the existence of an equivalent key makes CIEA-FOHS vulnerable to cryptographic attacks. Given the implementation of detailed cryptographic security analysis, these flaws can be avoided, thereby improving security.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, T.; Zhang, C.; Chen, C.; Hou, H.; Wei, H.; Hu, S.; Qiu, K. Security enhancement for OFDM-PON using Brownian motion and chaos in cell. Opt. Express 2018, 26, 22857–22865. [Google Scholar]
- Wu, T.; Zhang, C.; Chen, Y.; Cui, M.; Huang, H.; Zhang, Z.; Wen, H.; Zhao, X.; Qiu, K. Compressive sensing chaotic encryption algorithms for OFDM-PON data transmission. Opt. Express 2021, 29, 3669–3684. [Google Scholar]
- Wen, H.; Zhang, C.; Chen, P.; Chen, R.; Xu, J.; Liao, Y.; Liang, Z.; Shen, D.; Zhou, L.; Ke, J. A quantum chaotic image cryptosystem and its application in IoT secure communication. IEEE Access 2021, 1. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Tan, K.; Feng, B.; Lu, J. The Graph Structure of the Generalized Discrete Arnold’s Cat Map. IEEE Trans. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Xie, E.Y. When an attacker meets a cipher-image in 2018: A Year in Review. J. Inf. Secur. Appl. 2019, 48. [Google Scholar] [CrossRef] [Green Version]
- Akhshani, A.; Akhavan, A.; Mobaraki, A.; Lim, S.C.; Hassan, Z. Pseudo random number generator based on quantum chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 101–111. [Google Scholar]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar]
- Shen, C.; Yu, S.; Lü, J.; Chen, G. Designing Hyperchaotic Systems With Any Desired Number of Positive Lyapunov Exponents via A Simple Model. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 2380–2389. [Google Scholar]
- Askar, S.S.; Karawia, A.; Al-Khedhairi, A.; Al-Ammar, F.S. An algorithm of image encryption using logistic and two-dimensional chaotic economic maps. Entropy 2019, 21, 44. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Hua, Z.; Pun, C.; Philip Chen, C.L. Cascade Chaotic System with Applications. IEEE Trans. Cybern. 2015, 45, 2001–2012. [Google Scholar]
- Wen, H.; Yu, S. Cryptanalysis of an image encryption cryptosystem based on binary bit planes extraction and multiple chaotic maps. Eur. Phys. J. Plus 2019, 134, 1–16. [Google Scholar]
- Wen, H.; Yu, S.; Lü, J. Breaking an Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy 2019, 21, 246. [Google Scholar] [CrossRef] [Green Version]
- Shafique, A.; Shahid, J. Novel image encryption cryptosystem based on binary bit planes extraction and multiple chaotic maps. Eur. Phys. J. Plus 2018, 133, 331. [Google Scholar]
- Song, C.; Qiao, Y. A novel image encryption algorithm based on DNA encoding and spatiotemporal chaos. Entropy 2015, 17, 6954–6968. [Google Scholar]
- Xie, Y.; Li, C.; Yu, S.; Lü, J. On the cryptanalysis of Fridrich’s chaotic image encryption scheme. Signal Process. 2017, 132, 150–154. [Google Scholar]
- Chen, L.; Ma, B.; Zhao, X.; Wang, S. Differential cryptanalysis of a novel image encryption algorithm based on chaos and Line map. Nonlinear Dyn. 2016, 87, 1797–1807. [Google Scholar]
- Li, C.; Lin, D.; Lü, J. Cryptanalyzing an Image-Scrambling Encryption Algorithm of Pixel Bits. IEEE Multimed. 2017, 3, 64–71. [Google Scholar]
- Wang, L.; Sun, K.; Peng, Y.; He, S. Chaos and complexity in a fractional-order higher-dimensional multicavity chaotic map. Chaos Solitons Fractals 2020, 131, 109488. [Google Scholar]
- Peng, D.; Sun, K.; He, S.; Zhang, L.; Alamodi, A.O.A. Numerical analysis of a simplest fractional-order hyperchaotic system. Theor. Appl. Mech. Lett. 2019, 9, 220–228. [Google Scholar]
- He, S.; Sun, K.; Wang, H. Dynamics and synchronization of conformable fractional-order hyperchaotic systems using the Homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 146–164. [Google Scholar]
- Chai, X.; Bi, J.; Gan, Z.; Liu, X.; Zhang, Y.; Chen, Y. Color image compression and encryption scheme based on compressive sensing and double random encryption strategy. Signal Process. 2020, 176, 107684. [Google Scholar]
- Chai, X.; Wu, H.; Gan, Z.; Han, D.; Zhang, Y.; Chen, Y. An efficient approach for encrypting double color images into a visually meaningful cipher image using 2D compressive sensing. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Zhang, Y. A chaotic image encryption algorithm based on random dynamic mixing. Opt. Laser Technol. 2021, 138, 106837. [Google Scholar]
- Hua, Z.; Zhu, Z.; Yi, S.; Zhang, Z.; Huang, H. Cross-plane colour image encryption using a two-dimensional logistic tent modular map. Inf. Sci. 2021, 546, 1063–1083. [Google Scholar]
- Kamal, F.M.; Elsonbaty, A.; Elsaid, A. A novel fractional nonautonomous chaotic circuit model and its application to image encryption. Chaos Solitons Fractals 2021, 144, 110686. [Google Scholar]
- Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive control for fractional order induced chaotic fuzzy cellular neural networks and its application to image encryption. Inf. Sci. 2019, 491, 74–89. [Google Scholar]
- Yang, F.; Mou, J.; Liu, J.; Ma, C.; Yan, H. Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application. Signal Process. 2020, 169, 107373. [Google Scholar]
- Lahdir, M.; Hamiche, H.; Kassim, S.; Tahanout, M.; Kemih, K.; Addouche, S. A novel robust compression-encryption of images based on SPIHT coding and fractional-order discrete-time chaotic system. Opt. Laser Technol. 2019, 109, 534–546. [Google Scholar]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar]
- Yu, S.; Zhou, N.; Gong, L.; Nie, Z. Optical image encryption algorithm based on phase-truncated short-time fractional Fourier transform and hyper-chaotic system. Opt. Lasers Eng. 2020, 124, 105816. [Google Scholar]
- Sayed, W.S.; Radwan, A.G. Generalized switched synchronization and dependent image encryption using dynamically rotating fractional-order chaotic systems. AEU–Int. J. Electron. Commun. 2020, 123, 153268. [Google Scholar]
- Yang, Y.; Guan, B.; Li, J.; Li, D.; Zhou, Y.; Shi, W. Image compression-encryption scheme based on fractional order hyper-chaotic systems combined with 2D compressed sensing and DNA encoding. Opt. Laser Technol. 2019, 119, 105661. [Google Scholar]
- Fridrich, J. Symmetric Ciphers Based On Two-Dimensional Chaotic Maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar]
- Zhao, J.; Wang, S.; Chang, Y.; Li, X. A novel image encryption scheme based on an improper fractional-order chaotic system. Nonlinear Dyn. 2015, 80, 1721–1729. [Google Scholar]
- Norouzi, B.; Mirzakuchaki, S. Breaking a novel image encryption scheme based on an improper fractional order chaotic system. Multimed. Tools Appl. 2017, 76, 1817–1826. [Google Scholar]
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2010, 31, 347–354. [Google Scholar]
- Zhou, G.; Zhang, D.; Liu, Y.; Yuan, Y.; Liu, Q. A novel image encryption algorithm based on chaos and Line map. Neurocomputing 2015, 169, 150–157. [Google Scholar]
- Huang, X.; Zhao, Z.; Wang, Z.; Li, Y. Chaos and hyperchaos in fractional-order cellular neural networks. Neurocomputing 2012, 94, 13–21. [Google Scholar]
- Wang, Z.; Huang, X.; Li, Y.; Song, X. Image encryption based on a delayed fractional-order chaotic logistic system. Chin. Phys. B 2013, 22, 010504. [Google Scholar]
- Zhang, L.; Sun, K.; Liu, W.; He, S. A novel color image encryption scheme using fractional-order hyperchaotic system and DNA sequence operations. Chin. Phys. B 2017, 26, 100504. [Google Scholar]
- Huang, X.; Sun, T.; Li, Y.; Liang, J. A Color Image Encryption Algorithm Based on a Fractional-Order Hyperchaotic System. Entropy 2015, 17, 28–38. [Google Scholar]
- Li, C.; Liu, Y.; Zhang, L.Y.; Chen, M.Z.Q. Breaking a chaotic image encryption algorithm based on modulo addition and XOR operation. Int. J. Bifurc. Chaos 2013, 23, 1350075. [Google Scholar]
- Zhang, L.Y.; Liu, Y.; Pareschi, F.; Zhang, Y.; Wong, K.; Rovatti, R.; Setti, G. On the Security of a Class of Diffusion Mechanisms for Image Encryption. IEEE Trans. Cybern. 2018, 48, 1163–1175. [Google Scholar]
- Preishuber, M.; Hütter, S.K.T.; Uhl, A. Depreciating Motivation and Empirical Security Analysis of Chaos-Based Image and Video Encryption. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2137–2150. [Google Scholar]





| Ciphers | Broken by | Attack Methods |
|---|---|---|
| Fridrich et al. [34] in 1998 | Xie et al. [16] in 2017 | Chosen-ciphertext attack |
| Zhao et al. [35] in 2015 | Norouzi et al. [36] in 2017 | Chosen-plaintext attack |
| Ye [37] in 2010 | Li et al. [18] in 2017 | Cipher-only attack |
| Zhou [38] in 2015 | Chen et al. [17] in 2016 | Differential cryptanalysis |
| Song et al. [15] in 2015 | Wen et al. [13] in 2019 | Chosen-plaintext/cipertext attacks |
| Shafique et al. [14] in 2018 | Wen et al. [12] in 2019 | Chosen-plaintext attack |
| Rule | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Permutation status | ||||||
| Images | Sizes | Encrytion Time | Attacking Diffusion | Attacking Permutation | Totol Attacking Time | |||
|---|---|---|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 1 | Step 2 | ||||
| Figure 5a | 2 × 2 × 3 | 0.0280 | 0.1559 | 0.1811 | 1.0297 | 0.0244 | 2.7151 | 4.1502 |
| Figure 13b | 100 × 100 × 3 | 0.1539 | 0.0920 | 19.6092 | 1.1407 | 0.2764 | 2.7102 | 24.0427 |
| Figure 13d | 300 × 200 × 3 | 0.3280 | 0.5092 | 101.7737 | 0.7872 | 0.9055 | 2.4353 | 106.8545 |
| Figure 12e | 256 × 256 × 3 | 0.6391 | 0.6913 | 120.4768 | 1.6147 | 1.9642 | 3.7725 | 129.4039 |
| Figure 13f | 512 × 512 × 3 | 3.5386 | 2.8134 | 988.3704 | 1.9930 | 4.2884 | 5.0459 | 1004.4617 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, H.; Zhang, C.; Huang, L.; Ke, J.; Xiong, D. Security Analysis of a Color Image Encryption Algorithm Using a Fractional-Order Chaos. Entropy 2021, 23, 258. https://doi.org/10.3390/e23020258
Wen H, Zhang C, Huang L, Ke J, Xiong D. Security Analysis of a Color Image Encryption Algorithm Using a Fractional-Order Chaos. Entropy. 2021; 23(2):258. https://doi.org/10.3390/e23020258
Chicago/Turabian StyleWen, Heping, Chongfu Zhang, Lan Huang, Juxin Ke, and Dongqing Xiong. 2021. "Security Analysis of a Color Image Encryption Algorithm Using a Fractional-Order Chaos" Entropy 23, no. 2: 258. https://doi.org/10.3390/e23020258
APA StyleWen, H., Zhang, C., Huang, L., Ke, J., & Xiong, D. (2021). Security Analysis of a Color Image Encryption Algorithm Using a Fractional-Order Chaos. Entropy, 23(2), 258. https://doi.org/10.3390/e23020258






