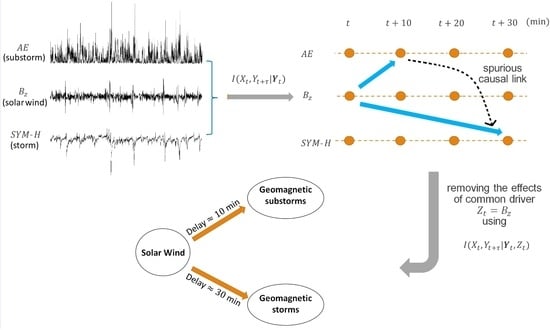
Causality and Information Transfer Between the Solar Wind and the Magnetosphere–Ionosphere System
Abstract
1. Introduction
2. Data Description
3. Overview of Methods
3.1. Measuring Dependence with Mutual Information
3.2. Inference of Causality and Time-Delayed Information Transfer
3.3. Linear-Gaussian CMI
3.4. Liang Information Flow
3.5. Interventional Causality
3.6. Statistical Evaluation with Surrogate Data
4. Results and Discussion
4.1. Causality and Time Delays
4.2. Linear Mass-Energy Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwenn, R. Space weather: The solar perspective. Living Rev. Sol. Phys. 2006, 3, 1–72. [Google Scholar] [CrossRef]
- Chang, T. Low-dimensional behavior and symmetry breaking of stochastic systems near criticality-can these effects be observed in space and in the laboratory? IEEE Trans. Plasma Sci. 1992, 20, 691–694. [Google Scholar] [CrossRef]
- Consolini, G. Self-organized criticality: A new paradigm for the magnetotail dynamics. Fractals 2002, 10, 275–283. [Google Scholar] [CrossRef]
- Valdivia, J.A.; Rogan, J.; Muñoz, V.; Toledo, B.A.; Stepanova, M. The magnetosphere as a complex system. Adv. Space Res. 2013, 51, 1934–1941. [Google Scholar] [CrossRef]
- Watkins, N.; Freeman, M.; Chapman, S.; Dendy, R. Testing the SOC hypothesis for the magnetosphere. J. Atmos. Sol. Terr. Phys. 2001, 63, 1435–1445. [Google Scholar] [CrossRef][Green Version]
- Balasis, G.; Daglis, I.; Kapiris, P.; Mandea, M.; Vassiliadis, D.; Eftaxias, K. From pre-storm activity to magnetic storms: A transition described in terms of fractal dynamics. Ann. Geophys. 2006, 24, 3557–3567. [Google Scholar] [CrossRef]
- Consolini, G.; De Michelis, P.; Tozzi, R. On the Earth’s magnetospheric dynamics: Nonequilibrium evolution and the fluctuation theorem. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Pulkkinen, T.; Palmroth, M.; Tanskanen, E.; Ganushkina, N.Y.; Shukhtina, M.; Dmitrieva, N. Solar wind—Magnetosphere coupling: A review of recent results. J. Atmos. Sol. Terr. Phys. 2007, 69, 256–264. [Google Scholar] [CrossRef]
- Akasofu, S.I. Polar Magnetic Substorm. In Polar and Magnetospheric Substorms; D. Reidell: Norwell, MA, USA, 1968. [Google Scholar]
- Gonzalez, W.; Joselyn, J.A.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.; Vasyliunas, V. What is a geomagnetic storm? J. Geophys. Res. Space Phys. 1994, 99, 5771–5792. [Google Scholar] [CrossRef]
- Kamide, Y.; Baumjohann, W.; Daglis, I.; Gonzalez, W.; Grande, M.; Joselyn, J.; McPherron, R.; Phillips, J.; Reeves, E.; Rostoker, G.; et al. Current understanding of magnetic storms: Storm-substorm relationships. J. Geophys. Res. Space Phys. 1998, 103, 17705–17728. [Google Scholar] [CrossRef]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785–801. [Google Scholar] [CrossRef]
- Wanliss, J.A.; Showalter, K.M. High-resolution global storm index: Dst versus SYM-H. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Sharma, A.S.; Baker, D.N.; Grande, M.; Kamide, Y.; Lakhina, G.S.; McPherron, R.M.; Reeves, G.D.; Rostoker, G.; Vondrak, R.; Zelenyiio, L. The Storm-Substorm Relationship: Current Understanding and Outlook. In Disturbances in Geospace: The Storm-Substorm Relationship; American Geophysical Union (AGU): Washington, DC, USA, 2003; pp. 1–14. [Google Scholar]
- Akasofu, S.I.; Cain, J.C.; Chapman, S. The magnetic field of a model radiation belt, numerically computed. J. Geophys. Res. 1961, 66, 4013–4026. [Google Scholar] [CrossRef]
- Alberti, T.; Consolini, G.; Lepreti, F.; Laurenza, M.; Vecchio, A.; Carbone, V. Timescale separation in the solar wind-magnetosphere coupling during St. Patrick’s Day storms in 2013 and 2015. J. Geophys. Res. Space Phys. 2017, 122, 4266–4283. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Materassi, M.; Tozzi, R. An information theory approach to the storm-substorm relationship. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Materassi, M.; Ciraolo, L.; Consolini, G.; Smith, N. Predictive Space Weather: An information theory approach. Adv. Space Res. 2011, 47, 877–885. [Google Scholar] [CrossRef]
- Johnson, J.R.; Wing, S. External versus internal triggering of substorms: An information-theoretical approach. Geophys. Res. Lett. 2014, 41, 5748–5754. [Google Scholar] [CrossRef]
- Wing, S.; Johnson, J.R.; Camporeale, E.; Reeves, G.D. Information theoretical approach to discovering solar wind drivers of the outer radiation belt. J. Geophys. Res. Space Phys. 2016, 121, 9378–9399. [Google Scholar] [CrossRef]
- Runge, J.; Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Donner, R.V. Common solar wind drivers behind magnetic storm–magnetospheric substorm dependency. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Stumpo, M.; Consolini, G.; Alberti, T.; Quattrociocchi, V. Measuring Information Coupling between the Solar Wind and the Magnetosphere–Ionosphere System. Entropy 2020, 22, 276. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef] [PubMed]
- Runge, J.; Heitzig, J.; Marwan, N.; Kurths, J. Quantifying causal coupling strength: A lag-specific measure for multivariate time series related to transfer entropy. Phys. Rev. E 2012, 86, 061121. [Google Scholar] [CrossRef]
- Perreault, P.; Akasofu, S. A study of geomagnetic storms. Geophys. J. Int. 1978, 54, 547–573. [Google Scholar] [CrossRef]
- Klimas, A.; Vassiliadis, D.; Baker, D.; Roberts, D. The organized nonlinear dynamics of the magnetosphere. J. Geophys. Res. Space Phys. 1996, 101, 13089–13113. [Google Scholar] [CrossRef]
- Iyemori, T. Storm-time magnetospheric currents inferred from mid-latitude geomagnetic field variations. J. Geomag. Geoelec. 1990, 42, 1249–1265. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Paluš, M. Detecting nonlinearity in multivariate time series. Phys. Lett. A 1996, 213, 138–147. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; J. Wiley: New York, NY, USA, 1991. [Google Scholar]
- Paluš, M.; Albrecht, V.; Dvořák, I. Information theoretic test for nonlinearity in time series. Phys. Lett. A 1993, 175, 203–209. [Google Scholar] [CrossRef]
- Paluš, M.; Komárek, V.; Hrnčíř, Z.; Štěrbová, K. Synchronization as adjustment of information rates: Detection from bivariate time series. Phys. Rev. E 2001, 63, 046211. [Google Scholar] [CrossRef] [PubMed]
- Hlaváčková-Schindler, K.; Paluš, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar] [CrossRef]
- Paluš, M.; Vejmelka, M. Directionality of coupling from bivariate time series: How to avoid false causalities and missed connections. Phys. Rev. E 2007, 75, 056211. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D.A., Young, L.S., Eds.; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef] [PubMed]
- Paluš, M. Multiscale atmospheric dynamics: Cross-frequency phase-amplitude coupling in the air temperature. Phys. Rev. Lett. 2014, 112, 078702. [Google Scholar] [CrossRef]
- Wibral, M.; Pampu, N.; Priesemann, V.; Siebenhühner, F.; Seiwert, H.; Lindner, M.; Lizier, J.T.; Vicente, R. Measuring information-transfer delays. PLoS ONE 2013, 8, e55809. [Google Scholar] [CrossRef]
- San Liang, X. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef]
- Aurell, E.; Del Ferraro, G. Causal analysis, correlation-response, and dynamic cavity. J. Phys. Conf. Ser. 2016, 699, 012002. [Google Scholar] [CrossRef]
- Baldovin, M.; Cecconi, F.; Vulpiani, A. Understanding causation via correlations and linear response theory. Phys. Rev. Res. 2020, 2, 043436. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation–dissipation: Response theory in statistical physics. Phys. Rep. 2008, 461, 111–195. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Kraskov, A.; Kreuz, T.; Grassberger, P. Performance of different synchronization measures in real data: A case study on electroencephalographic signals. Phys. Rev. E 2002, 65, 041903. [Google Scholar] [CrossRef]
- Paluš, M.; Hoyer, D. Detecting nonlinearity and phase synchronization with surrogate data. IEEE Eng. Med. Biol. Mag. 1998, 17, 40–45. [Google Scholar] [CrossRef]
- Maggiolo, R.; Hamrin, M.; De Keyser, J.; Pitkänen, T.; Cessateur, G.; Gunell, H.; Maes, L. The delayed time response of geomagnetic activity to the solar wind. J. Geophys. Res. Space Phys. 2017, 122, 11–109. [Google Scholar] [CrossRef]
- Daglis, I.A.; Thorne, R.M.; Baumjohann, W.; Orsini, S. The terrestrial ring current: Origin, formation, and decay. Rev. Geophys. 1999, 37, 407–438. [Google Scholar] [CrossRef]
- Fok, M.C.; Moore, T.E.; Delcourt, D.C. Modeling of inner plasma sheet and ring current during substorms. J. Geophys. Res. Space Phys. 1999, 104, 14557–14569. [Google Scholar] [CrossRef]
- Ganushkina, N.Y.; Pulkkinen, T.; Fritz, T. Role of substorm-associated impulsive electric fields in the ring current development during storms. Ann. Geophys. 2005, 23, 579–591. [Google Scholar] [CrossRef]
- Paluš, M.; Krakovská, A.; Jakubík, J.; Chvosteková, M. Causality, dynamical systems and the arrow of time. Chaos 2018, 28, 075307. [Google Scholar] [CrossRef]
- Chvosteková, M.; Jakubík, J.; Krakovská, A. Granger causality on forward and reversed time series. Entropy 2021, in press. [Google Scholar]
- Runge, J.; Petoukhov, V.; Donges, J.F.; Hlinka, J.; Jajcay, N.; Vejmelka, M.; Hartman, D.; Marwan, N.; Paluš, M.; Kurths, J. Identifying causal gateways and mediators in complex spatio-temporal systems. Nat. Commun. 2015, 6, 1–10. [Google Scholar] [CrossRef]
- Stramaglia, S.; Cortes, J.M.; Marinazzo, D. Synergy and redundancy in the Granger causal analysis of dynamical networks. New J. Phys. 2014, 16, 105003. [Google Scholar] [CrossRef]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Bertschinger, N.; Jost, J.; Wibral, M. Information decomposition of target effects from multi-source interactions: Perspectives on previous, current and future work. Entropy 2018, 20, 307. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using non-extensive Tsallis entropy. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Investigating dynamical complexity in the magnetosphere using various entropy measures. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Balasis, G.; Donner, R.V.; Potirakis, S.M.; Runge, J.; Papadimitriou, C.; Daglis, I.A.; Eftaxias, K.; Kurths, J. Statistical mechanics and information-theoretic perspectives on complexity in the earth system. Entropy 2013, 15, 4844–4888. [Google Scholar] [CrossRef]
- Balasis, G.; Papadimitriou, C.; Boutsi, A.Z.; Daglis, I.A.; Giannakis, O.; Anastasiadis, A.; De Michelis, P.; Consolini, G. Dynamical complexity in Swarm electron density time series using Block entropy. EPL Europhys. Lett. 2020, 131, 69001. [Google Scholar] [CrossRef]
- De Michelis, P.; Pignalberi, A.; Consolini, G.; Coco, I.; Tozzi, R.; Pezzopane, M.; Giannattasio, F.; Balasis, G. On the 2015 St. Patrick’s Storm Turbulent State of the Ionosphere: Hints From the Swarm Mission. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027934. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Balasis, G.; Boutsi, A.Z.; Daglis, I.A.; Giannakis, O.; Anastasiadis, A.; Michelis, P.; Consolini, G. Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures. Entropy 2020, 22, 574. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manshour, P.; Balasis, G.; Consolini, G.; Papadimitriou, C.; Paluš, M. Causality and Information Transfer Between the Solar Wind and the Magnetosphere–Ionosphere System. Entropy 2021, 23, 390. https://doi.org/10.3390/e23040390
Manshour P, Balasis G, Consolini G, Papadimitriou C, Paluš M. Causality and Information Transfer Between the Solar Wind and the Magnetosphere–Ionosphere System. Entropy. 2021; 23(4):390. https://doi.org/10.3390/e23040390
Chicago/Turabian StyleManshour, Pouya, Georgios Balasis, Giuseppe Consolini, Constantinos Papadimitriou, and Milan Paluš. 2021. "Causality and Information Transfer Between the Solar Wind and the Magnetosphere–Ionosphere System" Entropy 23, no. 4: 390. https://doi.org/10.3390/e23040390
APA StyleManshour, P., Balasis, G., Consolini, G., Papadimitriou, C., & Paluš, M. (2021). Causality and Information Transfer Between the Solar Wind and the Magnetosphere–Ionosphere System. Entropy, 23(4), 390. https://doi.org/10.3390/e23040390