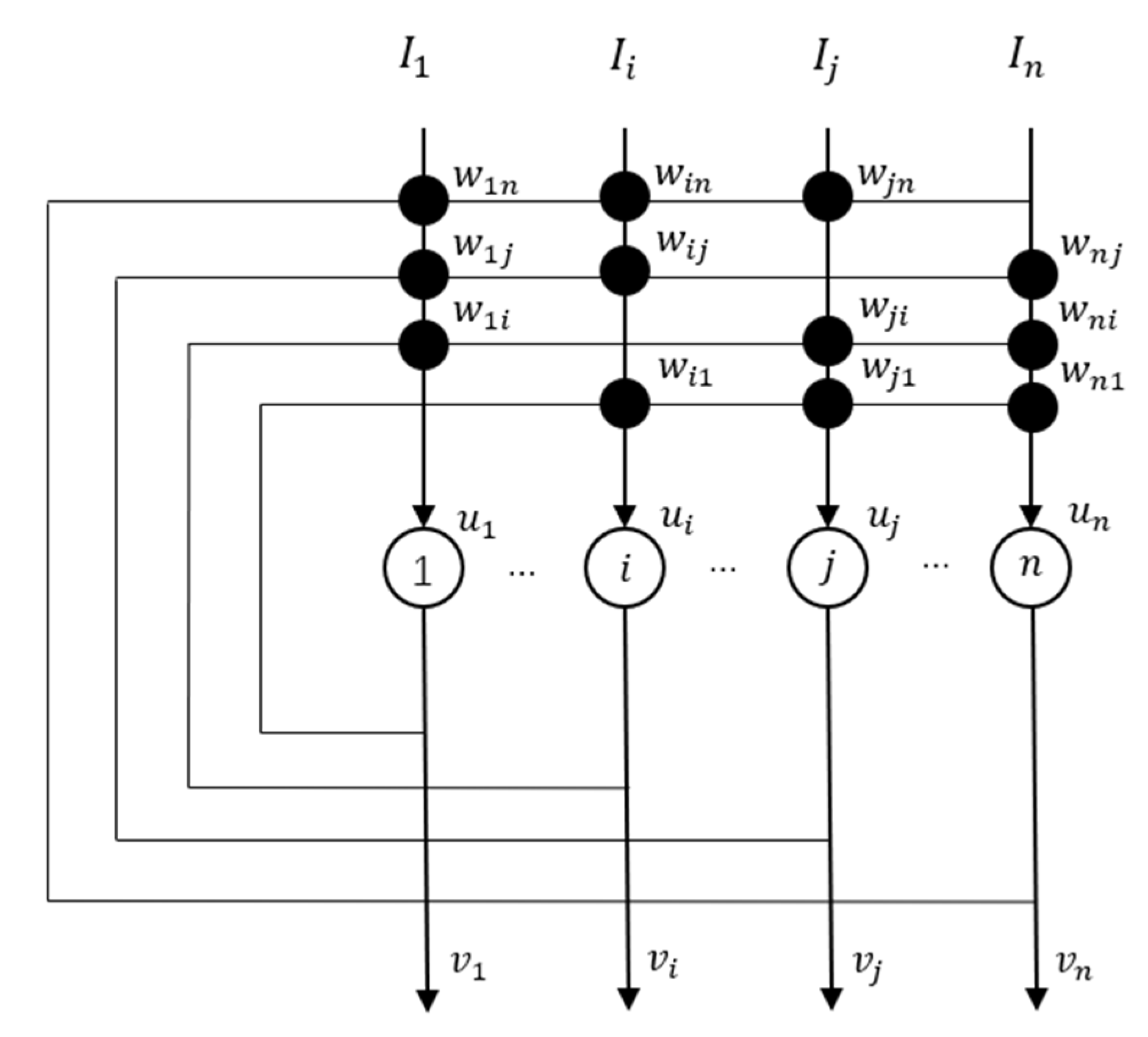
Figure 1.
The structure of conventional Hopfield network [
8].
Figure 1.
The structure of conventional Hopfield network [
8].
Figure 2.
The structure of positively self-feedbacked Hopfield network [
15].
Figure 2.
The structure of positively self-feedbacked Hopfield network [
15].
Figure 3.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 3.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
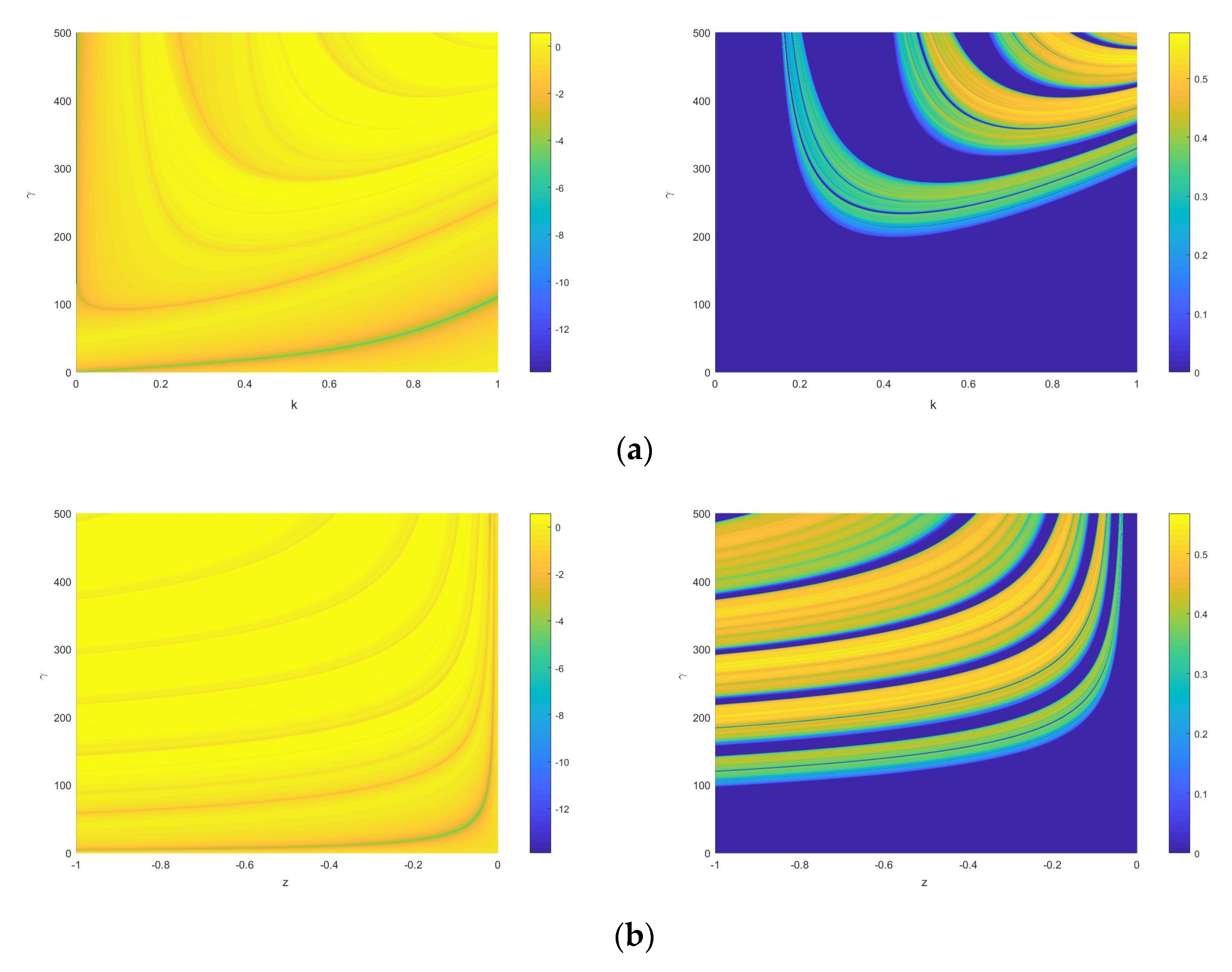
Figure 4.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 4.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 5.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 5.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 6.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 6.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 7.
Two-dimensional evolution diagram of Lyapunov exponent (the original), and two-dimensional evolution diagram of Lyapunov exponent (set to ) of (a) - for and ; (b) - for and ; (c) - for and ; (d) - for and ; (e) - for and ; (f) - for and .
Figure 7.
Two-dimensional evolution diagram of Lyapunov exponent (the original), and two-dimensional evolution diagram of Lyapunov exponent (set to ) of (a) - for and ; (b) - for and ; (c) - for and ; (d) - for and ; (e) - for and ; (f) - for and .
Figure 8.
The evolution diagram of Lyapunov exponent versus parameter for , , , and .
Figure 8.
The evolution diagram of Lyapunov exponent versus parameter for , , , and .
Figure 9.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 9.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 10.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 10.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 11.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 11.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 12.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 12.
Single-parameter bifurcation diagram of versus parameter and corresponding Lyapunov exponent diagram for , , and .
Figure 13.
Sensitivity to initial condition of (a) varied initial value, for , , , ; (b) varied , for , , , ; (c) varied , for , , , ; (d) varied , for , , , ; (e) varied , for , , , .
Figure 13.
Sensitivity to initial condition of (a) varied initial value, for , , , ; (b) varied , for , , , ; (c) varied , for , , , ; (d) varied , for , , , ; (e) varied , for , , , .
Figure 14.
Comparison of SE between different maps: (
a) ESNDS (z + 1) with
,
,
, ESNDS (k) with
,
,
, [
55] (
) with
, and [
55] (
) with
; (
b) ESNDS (z+1) with
,
,
, ESNDS (k) with
,
,
, [
48] (
), Sine map (
), and Logistic map (
).
Figure 14.
Comparison of SE between different maps: (
a) ESNDS (z + 1) with
,
,
, ESNDS (k) with
,
,
, [
55] (
) with
, and [
55] (
) with
; (
b) ESNDS (z+1) with
,
,
, ESNDS (k) with
,
,
, [
48] (
), Sine map (
), and Logistic map (
).
Figure 15.
Matrix permutating process of column.
Figure 15.
Matrix permutating process of column.
Figure 16.
Matrix permutating process of row.
Figure 16.
Matrix permutating process of row.
Figure 17.
Permutating process of matrix .
Figure 17.
Permutating process of matrix .
Figure 18.
Encryption result of some images. (a) the original images; (b) the encrypted images.
Figure 18.
Encryption result of some images. (a) the original images; (b) the encrypted images.
Figure 19.
Two-dimensional evolution diagram of Lyapunov exponent (set to ) of for , .
Figure 19.
Two-dimensional evolution diagram of Lyapunov exponent (set to ) of for , .
Figure 20.
Correlation analysis of image Lena. (a) horizontal, vertical and diagonal correlation of original image; (b) horizontal, vertical and diagonal correlation of encrypted image.
Figure 20.
Correlation analysis of image Lena. (a) horizontal, vertical and diagonal correlation of original image; (b) horizontal, vertical and diagonal correlation of encrypted image.
Figure 21.
The histogram of original images and encrypted images versus (a) Lena; (b) Cameraman; (c) Mandrill; (d) Peppers.
Figure 21.
The histogram of original images and encrypted images versus (a) Lena; (b) Cameraman; (c) Mandrill; (d) Peppers.
Figure 22.
Noise analysis: (a) 5% ‘salt & pepper’ noise of encrypted Lena; (b) 10% ‘salt & pepper’ noise of encrypted Lena; (c) 25% ‘salt & pepper’ noise of encrypted Lena; (d) 50% ‘salt & pepper’ noise of encrypted Lena; (e) decrypted Lena from (a); (f) decrypted Lena from (b); (g) decrypted Lena from (c); (h) decrypted Lena from (d).
Figure 22.
Noise analysis: (a) 5% ‘salt & pepper’ noise of encrypted Lena; (b) 10% ‘salt & pepper’ noise of encrypted Lena; (c) 25% ‘salt & pepper’ noise of encrypted Lena; (d) 50% ‘salt & pepper’ noise of encrypted Lena; (e) decrypted Lena from (a); (f) decrypted Lena from (b); (g) decrypted Lena from (c); (h) decrypted Lena from (d).
Figure 23.
Data loss analysis: (a) 25% data loss of encrypted Lena; (b) 25% data loss of encrypted Lena; (c) 50% data loss of encrypted Lena; (d) 50% data loss of encrypted Lena; (e) decrypted Lena from (a); (f) decrypted Lena from (b); (g) decrypted Lena from (c); (h) decrypted Lena from (d).
Figure 23.
Data loss analysis: (a) 25% data loss of encrypted Lena; (b) 25% data loss of encrypted Lena; (c) 50% data loss of encrypted Lena; (d) 50% data loss of encrypted Lena; (e) decrypted Lena from (a); (f) decrypted Lena from (b); (g) decrypted Lena from (c); (h) decrypted Lena from (d).
Table 1.
Implementation cost (second) of SNDS and self-feedbacked Hopfield networks.
Table 1.
Implementation cost (second) of SNDS and self-feedbacked Hopfield networks.
| Length of Sequence | | | | | |
|---|
| [21] | 0.006050 | 0.013739 | 0.079042 | 0.635034 | 6.286282 |
| [16] | 0.005240 | 0.012485 | 0.071335 | 0.581641 | 5.802823 |
| [19] | 0.008347 | 0.020941 | 0.120890 | 0.971717 | 9.612208 |
| SNDS | 0.001287 | 0.003032 | 0.017690 | 0.163250 | 1.723895 |
Table 2.
NIST SP800-22 test results of ESNDS.
Table 2.
NIST SP800-22 test results of ESNDS.
| Test Number | Subset | p-Value | Proportion | Test Result |
|---|
| 1 | Frequency | 0.675947 | 100/100 | Random |
| 2 | Block Frequency | 0.124338 | 100/100 | Random |
| 3 | Cumulative Sums | 0.771002 | 100/100 | Random |
| 4 | Runs | 0.965044 | 99/100 | Random |
| 5 | LongestRun | 0.734606 | 98/100 | Random |
| 6 | Rank | 0.609329 | 100/100 | Random |
| 7 | FFT | 0.229310 | 99/100 | Random |
| 8 | Non Over. Temp. | 0.328353 | 100/100 | Random |
| 9 | Over. Temp. | 0.617757 | 100/100 | Random |
| 10 | Universal | 0.384464 | 98/100 | Random |
| 11 | Appr. Entropy | 0.663306 | 99/100 | Random |
| 12 | Ran. Exc. | 0.130397 | 99/100 | Random |
| 13 | Ran. Exc. Var | 0.341983 | 100/100 | Random |
| 14 | Serial | 0.320912 | 98/100 | Random |
| 15 | Linear Complexity | 0.340430 | 100/100 | Random |
Table 3.
TestU01 test results of ESNDS.
Table 3.
TestU01 test results of ESNDS.
| Battery | Length of Sequences | Test Result |
|---|
| Rabbit | | Pass |
| | | Pass |
| Alphabit | | Pass |
| | | Pass |
| BlockAlphabit | | Pass |
| | | Pass |
Table 4.
Implementation cost (second) of ESNDS and different coupled chaotic maps.
Table 4.
Implementation cost (second) of ESNDS and different coupled chaotic maps.
| Length of Sequence | | | | | |
|---|
| [48] | 0.001985 | 0.03982 | 0.023012 | 0.216749 | 2.118830 |
| [55] | 0.001984 | 0.003283 | 0.011455 | 0.083962 | 0.875654 |
| ESNDS | 0.001650 | 0.003364 | 0.019894 | 0.167419 | 1.730450 |
Table 5.
Information entropy of different images.
Table 5.
Information entropy of different images.
| Image | Lena | Cameraman | Mandrill | Peppers |
|---|
| Original image | 7.4455 | 6.9719 | 7.3899 | 7.5327 |
| Encrypted image | 7.9993 | 7.9974 | 7.9993 | 7.9972 |
Table 6.
Correlation coefficient of various images.
Table 6.
Correlation coefficient of various images.
| | Original Image | Encrypted Image |
|---|
| Image | Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal |
|---|
| Lena | 0.9850 | 0.9719 | 0.9593 | 0.0043 | 0.0018 | 0.0003 |
| Cameraman | 0.9592 | 0.9340 | 0.9089 | 0.0002 | 0.0067 | 0.0012 |
| Mandrill | 0.8003 | 0.8763 | 0.7627 | 0.0003 | 0.0014 | 0.0013 |
| Peppers | 0.9651 | 0.9759 | 0.9457 | 0.0019 | 0.0008 | 0.0069 |
Table 7.
Correlation coefficient of various schemes.
Table 7.
Correlation coefficient of various schemes.
| | Encrypted Lena |
|---|
| Scheme | Horizontal | Vertical | Diagonal |
|---|
| [46] | 0.0024 | −0.0086 | 0.0402 |
| [49] | 0.0021 | 0.0051 | 0.0040 |
| [55] | 0.0046 | 0.0063 | 0.0023 |
| [56] | 0.0013 | 0.0018 | 0.0032 |
| [71] | −0.0084 | −0.0017 | −0.0019 |
| [72] | 0.0019 | 0.0038 | −0.0019 |
| [73] | 0.0030 | −0.0024 | −0.0034 |
| [74] | 0.0013 | −0.0141 | −0.0054 |
| [75] | 0.0035 | 0.0065 | 0.0036 |
| [76] | −0.0230 | 0.0019 | −0.0034 |
| Proposed | 0.0043 | 0.0018 | 0.0003 |
Table 8.
NPCR and UACI test result of different images ( and ).
Table 8.
NPCR and UACI test result of different images ( and ).
| Image | NPCR (%) | UACI (%) |
|---|
| Lena | 99.6037 | 33.5093 |
| Cameraman | 99.6201 | 33.4603 |
| Mandrill | 99.6029 | 33.4717 |
| Peppers | 99.6201 | 33.4738 |
Table 9.
Time complexity of different schemes.
Table 9.
Time complexity of different schemes.
| Scheme | Time Complexity |
|---|
| Proposed | |
| [51] | |
| [71] | |
| [75] | |
| [76] | |
Table 10.
Encryption time of proposed scheme.
Table 10.
Encryption time of proposed scheme.
| | Encryption Time (s) | |
|---|
| Image Size | | | | |
|---|
| Proposed scheme | 0.021936 | 0.086149 | 0.355649 | 1.406963 |