1. Introduction: Background and Motivations
The goal of the author is to methodologically contribute to an extension of the Sibson’s information radius [
1] and also concentrate on analysis of the specified families of distributions called exponential families [
2].
Let
denote a measurable space [
3] with sample space
and
-algebra
on the set
. The Jensen-Shannon divergence [
4] (JSD) between two probability measures
P and
Q (or probability distributions) on
is defined by:
where
denotes the Kullback–Leibler divergence [
5,
6] (KLD):
where
means that
P is absolutely continuous with respect to
Q [
3], and
is the Radon–Nikodym derivative of
P with respect to
Q. Equation (
2) can be rewritten using the chain rule as:
Consider a measure
for which both the Radon–Nikodym derivatives
and
exist (e.g.,
). Subsequently the Kullback–Leibler divergence can be rewritten as (see Equation (2.5) page 5 of [
5] and page 251 of the Cover & Thomas’ textbook [
6]):
Denote by
the set of all densities with full support
(Radon–Nikodym derivatives of probability measures with respect to
):
Subsequently, the Jensen-Shannon divergence [
4] between two densities
p and
q of
is defined by:
Often, one considers the Lebesgue measure [
3]
on
, where
is the Borel
-algebra, or the counting measure [
3]
on
where
is a countable set, for defining the measure space
.
The JSD belongs to the class of
f-divergences [
7,
8,
9] which are known as the invariant decomposable divergences of information geometry (see [
10], pp. 52–57). Although the KLD is asymmetric (i.e.,
), the JSD is symmetric (i.e.,
). The notation ‘:’ is used as a parameter separator to indicate that the parameters are not permutation invariant, and that the order of parameters is important.
In this work, a distance is a measure of dissimilarity between two objects and , which do not need to be symmetric or satisfy the triangle inequality of metric distances. A distance only satisfies the identity of indiscernibles: if and only if . When the objects and are probability densities with respect to , we call this distance a statistical distance, use the brackets to enclose the arguments of the statistical distance (i.e., ), and we have if and only if -almost everywhere.
The 2-point JSD of Equation (
4) can be extended to a weighted set of
n densities
(with positive
’s normalized to sum up to unity, i.e.,
) thus providing a diversity index, i.e., a
n-point JSD for
:
where
denotes the statistical mixture [
11] of the densities of
. We have
. We call
the Jensen-Shannon diversity index.
The KLD is also called the relative entropy since it can be expressed as the difference between the cross entropy
and the entropy
:
with the cross-entropy and entropy defined, respectively, by
Because
, we may say that the entropy is the self-cross-entropy.
When
is the Lebesgue measure, the Shannon entropy is also called the differential entropy [
6]. Although the discrete entropy
(i.e., entropy with respect to the counting measure) is always positive and bounded by
, the differential entropy may be negative (e.g., entropy of a Gaussian distribution with small variance).
The Jensen-Shannon divergence of Equation (
6) can be rewritten as:
The JSD representation of Equation (
12) is a Jensen divergence [
12] for the strictly convex negentropy
, since the entropy function
is strictly concave. Therefore, it is appropriate to call this divergence the Jensen-Shannon divergence.
Because
, it can be shown that the Jensen-Shannon diversity index is upper bounded by
, the discrete Shannon entropy. Thus, the Jensen-Shannon diversity index is bounded by
, and the 2-point JSD is bounded by
, although the KLD is unbounded and it may even be equal to
when the definite integral diverges (e.g., KLD between the standard Cauchy distribution and the standard Gaussian distribution). Another nice property of the JSD is that its square root yields a metric distance [
13,
14]. This property further holds for the quantum JSD [
15]. The JSD has gained interest in machine learning. See, for example, the Generative Adversarial Networks [
16] (GANs) in deep learning [
17], where it was proven that minimizing the GAN objective function by adversarial training is equivalent to minimizing a JSD.
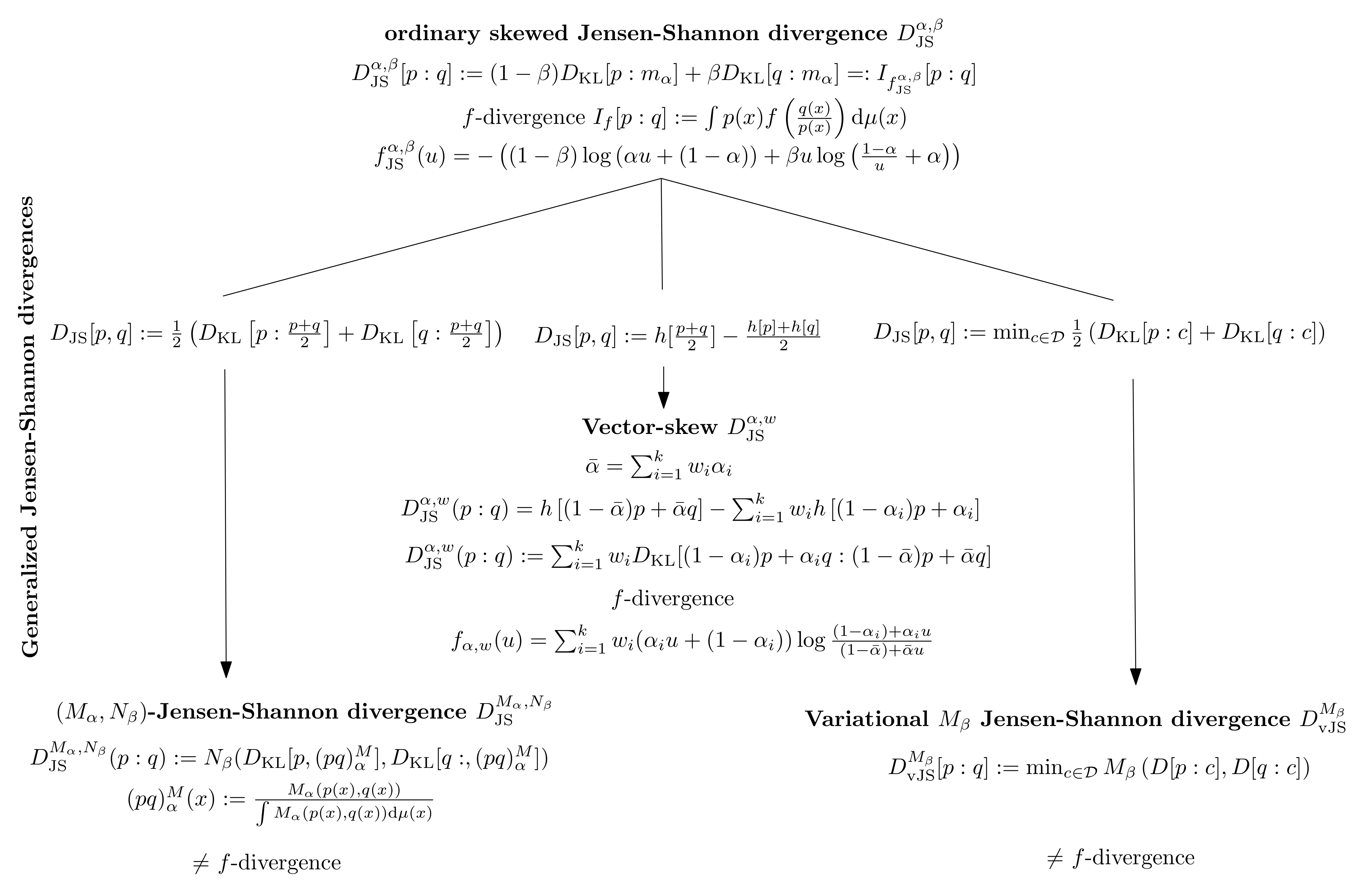
To delineate the different roles that are played by the factor
in the ordinary Jensen-Shannon divergence (i.e., in weighting the two KLDs and in weighting the two densities), let us introduce two scalars
, and define a generic
-skewed Jensen-Shannon divergence, as follows:
where
and
. This identity holds, because
is bounded by
, see [
18]. Thus, when
, we have
, since the self-cross entropy corresponds to the entropy:
.
A
f-divergence [
9,
19,
20] is defined for a convex generator
f, which is strictly convex at 1 (to satisfy the identity of the indiscernibles) and that satisfies
, by
where the right-hand-side follows from Jensen’s inequality [
20]. For example, the total variation distance
is a
f-divergence for the generator
:
. The generator
is convex on
, strictly convex at 1, and it satisfies
.
The
divergence is a
f-divergence
for the generator:
We check that the generator
is strictly convex, since, for any
and
, we have
when
.
The Jensen-Shannon principle of taking the average of the (Kullback–Leibler) divergences between the source parameters to the mid-parameter can be applied to other distances. For example, the Jensen–Bregman divergence is a Jensen-Shannon symmetrization of the Bregman divergence
[
12]:
where the Bregman divergence [
21]
is defined by
The Jensen–Bregman divergence
can also be written as an equivalent Jensen divergence
:
where
F is a strictly convex function ensuring
with equality if
.
Because of its use in various fields of information sciences [
22], various generalizations of the JSD have been proposed: These generalizations are either based on Equation (
5) [
23] or Equation (
12) [
18,
24,
25]. For example, the (arithmetic) mixture
in Equation (
6) was replaced by an abstract statistical mixture with respect to a generic mean
M in [
23] (e.g., the geometric mixture induced by the geometric mean), and the two KLDS defining the JSD in Equation (
5) was further averaged using another abstract mean
N, thus yielding the following generic
-Jensen-Shannon divergence [
23] (abbreviated as
-JSD):
where
denotes the statistical weighted
M-mixture:
Notice that, when
(the arithmetic mean), Equation (
23) of the
-JSD reduces to the ordinary JSD of Equation (
5). When the means
M and
N are symmetric, the
-JSD is symmetric.
In general, a weighted mean
for any
shall satisfy the in-betweeness property [
26] (i.e., a mean should be contained inside its extrema):
The three Pythagorean means defined for positive scalars and are classic examples of means:
The arithmetic mean ,
the geometric mean , and
the harmonic mean .
These Pythagorean means may be interpreted as special instances of another parametric family of means: The power means
defined for
(also called Hölder means). The power means can be extended to the full range
by using the property that
. The power means are homogeneous means:
for any
. We refer to the handbook of means [
27] to obtain definitions and principles of other means beyond these power means.
A weighted mean (also called barycenter) can be built from a non-weighted mean
(i.e.,
) by using the dyadic expansion of the real weight
, see [
28]. That is, we can define the weighted mean
for
with
and
k an integer. For example, consider a symmetric mean
. Subsequently, we get the following weighted means when
:
Let
be the unique dyadic expansion of the real number
, where the
’s are binary digits (i.e.,
). We define the weighted mean
of two positive reals
p and
q for a real weight
as
Choosing the abstract mean
M in accordance with the family
of the densities allows one to obtain closed-form formula for the
-JSDs that rely on definite integral calculations [
23]. For example, the JSD between two Gaussian densities does not admit a closed-form formula because of the log-sum integral, but the
-JSD admits a closed-form formula when using geometric statistical mixtures (i.e., when
). The calculus trick is to find a weighted mean
, such that, for two densities
and
, the weighted mean distribution
, where
is the normalizing coefficient and
. Thus, the integral calculation can be simply calculated as
since
, and, therefore,
. This trick has also been used in Bayesian hypothesis testing for upper bounding the probability of error between two densities of a parametric family of distributions by replacing the usual geometric mean (Section 11.7 of [
6], page 375) by a more general quasi-arithmetic mean [
29]. For example, the harmonic mean is well-suited to Cauchy distributions, and the power means to Student
t-distributions [
29].
As an application of these generalized JSDs, Deasy et al. [
30] used the skewed geometric JSD (namely, the
-JSD for
), which admits a closed-form formula between normal densities [
23], and showed how regularizing an optimization task with this G-JSD divergence improved reconstruction and generation of Variational AutoEncoders (VAEs).
More generally, instead of using the KLD, one can also use any arbitrary distance
D to define its JS-symmetrization, as follows:
These symmetrizations may further be skewed by using
and/or
for
and
, yielding the definition [
23]:
With these notations, the ordinary JSD is
, the
JS-symmetrization of the KLD with respect to the arithmetic means
and
.
The JS-symmetrization can be interpreted as the
-Jeffreys’ symmetrization of a generalization of Lin’s
-skewed
K-divergence [
4]
:
In this work, we consider symmetrizing an arbitrary distance
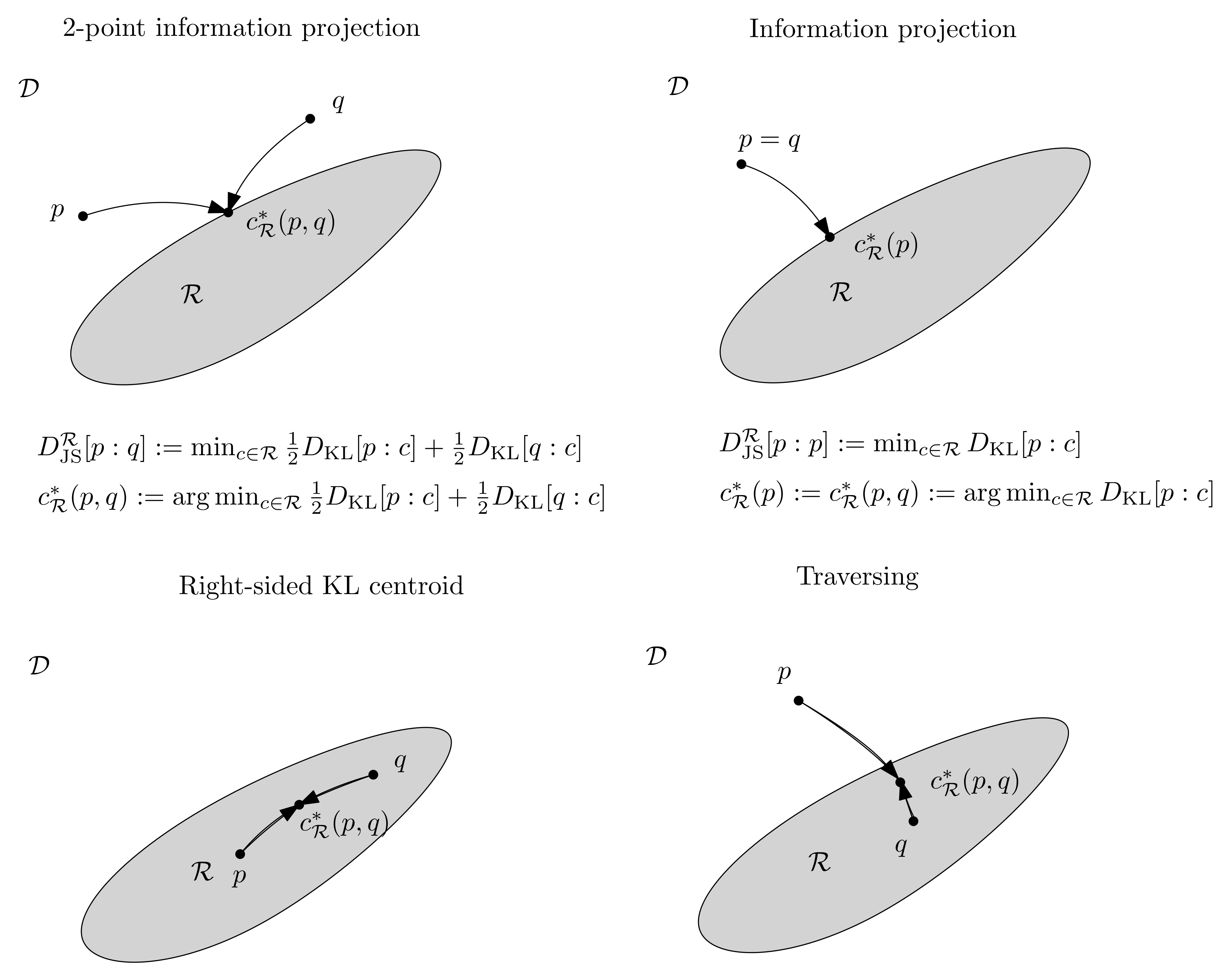
D (including the KLD), generalizing the Jensen-Shannon divergence by using a variational formula for the JSD. Namely, we observe that the Jensen-Shannon divergence can also be defined as the following minimization problem:
since the optimal density
c is proven unique using the calculus of variation [
1,
31,
32] and it corresponds to the mid density
, a statistical (arithmetic) mixture.
Proof. Let . We use the method of the Lagrange multipliers for the constrained optimization problem such that . Let us minimize . The density c realizing the minimum satisfies the Euler–Lagrange equation , where is the Lagrangian. That is, or, equivalently, . Parameter is then evaluated from the constraint : we get since . Therefore, we find that , the mid density of and . □
Considering Equation (
32) instead of Equation (
5) for defining the Jensen-Shannon divergence is interesting, because it allows one to consider a novel approach for generalizing the Jensen-Shannon divergence. This variational approach was first considered by Sibson [
1] to define the
-information radius of a set of weighted distributions while using Rényi
-entropies that are based on Rényi principled
-means [
33]. The
-information radius includes the Jensen-Shannon diversity index when
. Sibson’s work is our point of departure for generalizing the Jensen-Shannon divergence and proposing the Jensen-Shannon symmetrizations of arbitrary distances.
The paper is organized, as follows: in
Section 2, we recall the rationale and definitions of the Rényi
-entropy and the Rényi
-divergence [
33], and explain the information radius of Sibson [
1], which includes, as a special case, the ordinary Jensen-Shannon divergence and that can be interpreted as generalized skew Bhattacharyya distances. We report, in Theorem 2, a closed-form formula for calculating the information radius of order
between two densities of an exponential family when
is an integer. It is noteworthy to point out that Sibson’s work (1969) includes, as a particular case of the information radius, a definition of the JSD, prior to the well-known reference paper of Lin [
4] (1991). In
Section 3, we present the JS-symmetrization variational definition that is based on a generalization of the information radius with a generic mean (Equation (
88) and Definition 3). In
Section 4, we constrain the mixture density to belong to a prescribed class of (parametric) probability densities, like an exponential family [
2], and obtain a relative information radius generalizing information radius and related to the concept of information projections. Our Definition 5 generalizes the (relative) normal information radius of Sibson [
1], who considered the multivariate normal family (Proposition 4). We illustrate this notion of relative information radius by calculating the density of an exponential family minimizing the reverse Kullback–Leibler divergence between a mixture of densities of that exponential family (Proposition 6). Moreover, we get a semi-closed-form formula for the Kullback–Leibler divergence between the densities of two different exponential families (Proposition 5), generalizing the Fenchel–Young divergence [
34]. As an application of these relative variational JSDs, we touch upon the problems of clustering and quantization of probability densities in
Section 4.2. Finally, we conclude by summarizing our contributions and discussing related works in
Section 5.
2. Rényi Entropy and Divergence, and Sibson Information Radius
Rényi [
33] investigated a generalization of the four axioms of Fadeev [
35], yielding the unique Shannon entropy [
20]. In doing so, Rényi replaced the ordinary weighted arithmetic mean by a more general class of averaging schemes. Namely, Rényi considered the weighted quasi-arithmetic means [
36]. A weighted quasi-arithmetic mean can be induced by a strictly monotonous and continuous function
g, as follows:
where the
’s and the
’s are positive (the weights are normalized, so that
). Because
, we may assume without loss of generality that
g is a strictly increasing and continuous function. The quasi-arithmetic means were investigated independently by Kolmogorov [
36], Nagumo [
37], and de Finetti [
38].
For example, the power means
introduced earlier are quasi-arithmetic means for the generator
:
Rényi proved that, among the class of weighted quasi-arithmetic means, only the means induced by the family of functions
for
and
yield a proper generalization of Shannon entropy, nowadays called the Rényi
-entropy. The Rényi
-mean is
The Rényi
-means
are not power means: They are not homogeneous means [
31]. Let
. Subsequently, we have
and
. Indeed, we have
using the following first-order approximations:
and
.
To obtain an intuition of the Rényi entropy, we may consider generalized entropies derived from quasi-arithmetic means, as follows:
When
, we recover Shannon entropy. When
, we get
, called the collision entropy, since
, when
and
are independent and identically distributed random variables with
and
. When
, we get
The formula of Equation (
41) is the discrete Rényi
-entropy [
33], which can be defined more generally on a measure space
, as follows:
In the limit case
, the Rényi
-entropy converges to Shannon entropy:
. Rényi
-entropies are non-increasing with respect to increasing
:
for
. In the discrete case (i.e., counting measure
on a finite alphabet
), we can further define
for
(also called max-entropy or Hartley entropy). The Rényi
-entropy
is also called the min-entropy, since the sequence
is non-increasing with respect to increasing
.
Similarly, Rényi obtained the
-divergences for
and
(originally called information gain of order
):
generalizing the Kullback–Leibler divergence, since
. Rényi
-divergences are non-decreasing with respect to increasing
[
39]:
for
.
Sibson (Robin Sibson (1944–2017) is also renown for inventing the natural neighbour interpolation [
40]) [
1] considered both the Rényi
-divergence [
33]
and the Rényi
-weighted mean
to define the information radius
of order
of a weighted set
of densities
’s as the following minimization problem:
where
The Rényi
-weighted mean
can be rewritten as
where function
denotes the log-sum-exp (convex) function [
41,
42].
Notice that
, the Bhattacharyya
-coefficient [
12] (also called Chernoff
-coefficient [
43,
44]):
Thus, we have
The ordinary Bhattacharyya coefficient is obtained for
:
.
Sibson [
1] also considered the limit case
when defining the information radius:
Sibson reported the following theorem in his information radius study [
1]:
Theorem 1 (Theorem 2.2 and Corollary 2.3 of [
1])
. The optimal density is unique, and we have: Observe that does not depend on the (positive) weights.
The proof follows from the following decomposition of the information radius:
Because the proof is omitted in [
1], we report it here:
Proof. Let . We handle the three cases, depending on the values:
Case
: Let
. We have
. We obtain
Case
: we have
with
. Because
, we have
Case : we have , , and . We have Thus, .
□
It follows that
Thus we have
since
is minimized for
.
Notice that
is the upper envelope of the densities
’s normalized to be a density. Provided that the densities
’s intersect pairwise in at most
s locations (i.e.,
for
), we can efficiently compute this upper envelope using an output-sensitive algorithm [
45] of computational geometry.
When the point set is
with
, the information radius defines a (2-point) symmetric distance, as follows:
This family of symmetric divergences may be called the Sibson’s -divergences, and the Jensen-Shannon divergence is interpreted as a limit case when . Notice that, since we have and , we have . Notice that, for , the integral and logarithm operations are swapped as compared to for .
Theorem 2. When for an integer , the Sibson α-divergences between two densities and of an exponential family with cumulant function is available in closed form: Proof. Let
and
be two densities of an exponential family [
2] with cumulant function
and natural parameter space
. Without a loss of generality, we may consider a natural exponential family [
2] with densities written canonically as
for
. It can be shown that the cumulant function
is strictly convex and analytic on the open convex natural parameter space
[
2].
When
(i.e.,
), we have:
where
is the Bhattacharyya coefficient (with
). Using Theorem 3 of [
12], we have
so that we obtain the following closed-form formula:
Now, assume that
is an arbitrary integer, and let us apply the binomial expansion for
in the spirit of [
46,
47]:
Let
. Because
for
, we get by following the calculation steps in [
12]:
Notice that
, and
.
Thus, we get the following closed-form formula:
□
This closed-form formula applies, in particular, to the family
of (multivariate) normal distributions: In this case, the natural parameters
are expressed using both a vector parameter component
v and a matrix parameter component
M:
and the cumulant function is:
where
denotes the matrix determinant.
In general, the optimal density
yielding the information radius
can be interpreted as a generalized centroid (extending the notion of Fréchet means [
48]) with respect to
, where a
-centroid is defined by:
Definition 1 (
-centroid)
. Let be a normalized weighted parameter set, M a mean, and D a distance. Subsequently, the -centroid is defined as Here, we give a general definition of the
-centroid for an arbitrary distance (not necessarily a symmetric nor metric distance). The parameter set can either be probability measures having densities with respect to a given measure
or a set of vectors. In the first case, the distance
D is called a statistical distance. When the densities belong to a parametric family of densities
, the statistical distance
amounts to a parameter distance:
. For example, when all of the densities
’s belong to a same natural exponential family [
2]
with cumulant function
(i.e.,
) and sufficient statistic vector
, we have
, where
denotes the reverse Bregman divergence (by parameter order swapping) the Bregman divergence [
21]
defined by
Thus, we have
.
Let
be the parameter set corresponding to
. Define
Subsequently, we have the equivalent decomposition of Proposition 1:
with
. (this decomposition is used to prove Proposition 1 of [
21]). The quantity
was termed the Bregman information [
21,
49]. The Bregman information generalizes the variance that was obtained when the Bregman divergence is the squared Euclidean distance.
could also be called Bregman information radius according to Sibson. Because
, we can interpret the Bregman information as a Sibson’s information radius for densities of an exponential family with respect to the arithmetic mean
and the reverse Kullback–Leibler divergence:
. This observation yields us the JS-symmetrization of distances based on generalized information radii in
Section 3.
More generally, we may consider the densities belonging to a deformed
q-exponential family (see [
10], page 85–89 and the monograph [
50]). Deformed
q-exponential families generalize the exponential families, and include the
q-Gaussians [
10]. A common way to measure the statistical distance between two densities of a
q-exponential family is the
q-divergence [
10], which is related to Tsallis’ entropy [
51]. We may also define another statistical divergence between two densities of a
q-exponential family which amounts to Bregman divergence. For example, we refer to [
52] for details concerning the family of Cauchy distributions, which are
q-Gaussians for
.
Sibson proved that the information radii of any order are all upper bounded (Theorem 2.8 and Theorem 2.9 of [
1]) as follows:
We interpret Sibson’s upper bounds of Equations (
73)–(
75), as follows:
Proposition 2 (Information radius upper bound). The information radius of order α of a weighted set of distributions is upper bounded by the discrete Rényi entropy of order of the weight distribution: , where .
3. JS-Symmetrization of Distances Based on Generalized Information Radius
Let us give the following definitions generalizing the information radius (i.e., Jensen-Shannon symmetrization of the distance when ) and the ordinary Jensen-Shannon divergence:
Definition 2 (
-information radius)
. Let M be a weighted mean and D a distance. Subsequently, the generalized information radius for a weighted set of points (e.g., vectors or densities) is: Recall that we also defined the
-centroid in Definition 1 as follows:
When
, we recover the notion of Fréchet mean [
48]. Notice that, although the minimum
is unique, several generalized centroids
may potentially exist, depending on
. In particular, Definition 2 and Definition 1 apply when
D is a statistical distance, i.e., a distance between densities (Radon–Nikodym derivatives of corresponding probability measures with respect to a dominating measure
).
The generalized information radius can be interpreted as a diversity index or an n-point distance. When , we get the following (2-point) distances, which are considered as a generalization of the Jensen-Shannon divergence or Jensen-Shannon symmetrization:
Definition 3 (
M-vJS symmetrization of
D)
. Let M be a mean and D a statistical distance. Subsequently, the variational Jensen-Shannon symmetrization of D is defined by the formula of a generalized information radius: We use the acronym
to distinguish it with the JS-symmetrization reported in [
23]:
We recover Sibson’s information radius
induced by two densities
p and
q from Definition 3 as the
-vJS symmetrization of the Rényi divergence . We have
, which is the Bregman information [
21]. Notice that we may skew these generalized JSDs by taking weighted mean
instead of
M for
, yielding the general definition:
Definition 4 (Skew
-vJS symmetrization of
D)
. Let be a weighted mean and D a statistical distance. Subsequently, the variational skewed Jensen-Shannon symmetrization of D is defined by the formula of a generalized information radius: Example 1. For example, the skewed Jensen–Bregman divergence of Equation (20) can be interpreted as a Jensen-Shannon symmetrization of the Bregman divergence [12] since we have:Indeed, the Bregman barycenter is unique and it corresponds to , see [21]. The skewed Jensen–Bregman divergence can also be rewritten as an equivalent skewed Jensen divergence (see Equation (22)): Example 2. Consider a conformal Bregman divergence [53] that is defined bywhere is a conformal factor. Subsequently, we havewhere and . Notice that this definition is implicit and it can be made explicit when the centroid
is unique:
In particular, when
, the KLD, we obtain generalized skewed Jensen-Shannon divergences for
a weighted mean with
:
Example 3. Amari [31] obtained the -information radius and its corresponding unique centroid for , the α-divergence of information geometry [10] (page 67). Example 4. Brekelmans et al. [54] studied the geometric path between two distributions and of , where (with ) is the weighted geometric mean. They proved the variational formula: That is, is a - centroid, where is the reverse KLD. The corresponding -vJSD is studied is [23] and it is used in deep learning in [30]. It is interesting to study the link between -variational Jensen-Shannon symmetrization of D and the -JS symmetrization of [23]. In particular, the link between for averaging in the minimization and the mean for generating abstract mixtures. More generally, Brekelmans et al. [55] considered the α-divergences extended to positive measures (i.e., a separable divergence built as the different between a weighted arithmetic mean and a geometric mean [56]):and proved thatis a density of a likelihood ratio q-exponential family: for . That is, is the -generalized centroid, and the corresponding information radius is the variational JS symmetrization: Example 5. The q-divergence [57] between two densities of a q-exponential family amounts to a Bregman divergence [10,57]. Thus, for is a generalized information radius that amounts to a Bregman information. For the case in Sibson’s information radius, we find that the information radius is related to the total variation:
Proposition 3 (Lemma 2.4 [
1])
. :where denotes the total variation Proof. Because
, it follows that we have:
From Theorem 1, we have and, therefore, . □
Notice that, when
is a quasi-arithmetic mean, we may consider the divergence
, so that the centroid of the
-JS symmetrization is:
The generalized
-skewed Bhattacharyya divergence [
29] can also be considered with respect to a weighted mean
:
In particular, when
is a quasi-arithmetic weighted mean that is induced by a strictly continuous and monotone function
g, we have
Because
,
and
, we deduce that we have:
The information radius of Sibson for may be interpreted as generalized scaled -skewed Bhattacharyya divergences with respect to the power means , since we have .
5. Conclusions
To summarize, the ordinary Jensen-Shannon divergence has been defined in three equivalent ways in the literature:
The JSD Equation (
133) was studied by Sibson in 1969 within the wider scope of information radius [
1]: Sibson relied on the Rényi
-divergences (relative Rényi
-entropies [
77]) and recovered the ordinary Jensen-Shannon divergence as a particular case of the
-information radius when
and
points. The
-information radii are related to generalized Bhattacharyya distances with respect to power means and the total variation distance in the limit case of
.
Lin [
4] investigated the JSD Equation (
134) in 1991 with its connection to the JSD defined in Equation (
134)). In Lin [
4], the JSD is interpreted as the arithmetic symmetrization of the
K-divergence [
24]. Generalizations of the JSD based on Equation (
134) were proposed in [
23] using a generic mean instead of the arithmetic mean. One motivation was to obtain a closed-form formula for the geometric JSD between multivariate Gaussian distributions, which relies on the geometric mixture (see [
30] for a use case of that formula in deep learning). Indeed, the ordinary JSD between Gaussians is not available in closed-form (not analytic). However, the JSD between Cauchy distributions admit a closed-form formula [
78], despite the calculation of a definite integral of a log-sum term. Instead of using an abstract mean to define a mid-distribution of two densities, one may also consider the mid-point of a geodesic linking these two densities (the arithmetic means
is interpreted as a geodesic midpoint). Recently, Li [
79] investigated the transport Jensen-Shannon divergence as a symmetrization of the Kullback–Leibler divergence in the
-Wasserstein space. See Section 5.4 of [
79] and the closed-form formula of Equation (
18) obtained for the transport Jensen-Shannon divergence between two multivariate Gaussian distributions.
The generalization of the identity between the JSD of Equation (
134) and the JSD of Equation (
135) was studied while using a skewing vector in [
18]. Although the JSD is a
f-divergence [
8,
18], the Sibson-
M Jensen-Shannon symmetrization of a distance does not belong, in general, to the class of
f-divergences. The variational JSD definition of Equation (
133) is implicit, while the definitions of Equations (
134) and (
135) are explicit because the unique optimal centroid
has been plugged into the objective function that was minimized by Equation (
133).
In this paper, we proposed a generalization of the Jensen-Shannon divergence based on the variational definition of the ordinary Jensen-Shannon divergence based on the variational JSD definition of Equation (
133):
. We introduced the Jensen-Shannon symmetrization of an arbitrary divergence
D by considering a generalization of the information radius with respect to an abstract weighted mean
:
. Notice that, in the variational JSD, the mean
is used for averaging divergence values, while the mean
in the
JSD is used to define generic statistical mixtures. We also consider relative variational JS symmetrization when the centroid has to belong to a prescribed family of densities. For the case of exponential family, we showed how to compute the relative centroid in closed form, thus extending the pioneering work of Sibson, who considered the relative normal centroid used to calculate the relative normal information radius.
Figure 2 illustrates the three generalizations of the ordinary skewed Jensen-Shannon divergence. Notice that, in general, the
-JSDs and the variational JDSs are not
f-divergences (except in the ordinary case).
In a similar vein, Chen et al. [
80] considered the following minimax symmetrization of the scalar Bregman divergence [
81]:
where
denotes the scalar Bregman divergence induced by a strictly convex and smooth function
f:
They proved that
yields a metric when
, and extend the definition to the vector case and conjecture that the square-root metrization still holds in the multivariate case. In a sense, this definition geometrically highlights the notion of radius, since the minmax optimization amount to find a smallest enclosing ball enclosing [
82] the source distributions. The circumcenter, also called the Chebyshev center [
83], is then the mid-distribution instead of the centroid for the information radius. The term "information radius” is well-suited to measure the distance between two points for an arbitrary distance
D. Indeed, the JS-symmetrization of
D is defined by
. When
is the Euclidean distance, we have
, and
(i.e., the radius being half of the diameter
). Thus,
; hence, the term chosen by Sibson [
1] for
: information radius. Besides providing another viewpoint, variational definitions of divergences have proven to be useful in practice (e.g., for estimation). For example, a variational definition of the Rényi divergence generalizing the Donsker–Varadhan variational formula of the KLD is given in [
84], which is used to estimate the Rényi Divergences.