Refined Composite Multi-Scale Reverse Weighted Permutation Entropy and Its Applications in Ship-Radiated Noise
Abstract
1. Introduction
2. Refined Composite Multi-Scale Reverse Weighted Permutation Entropy
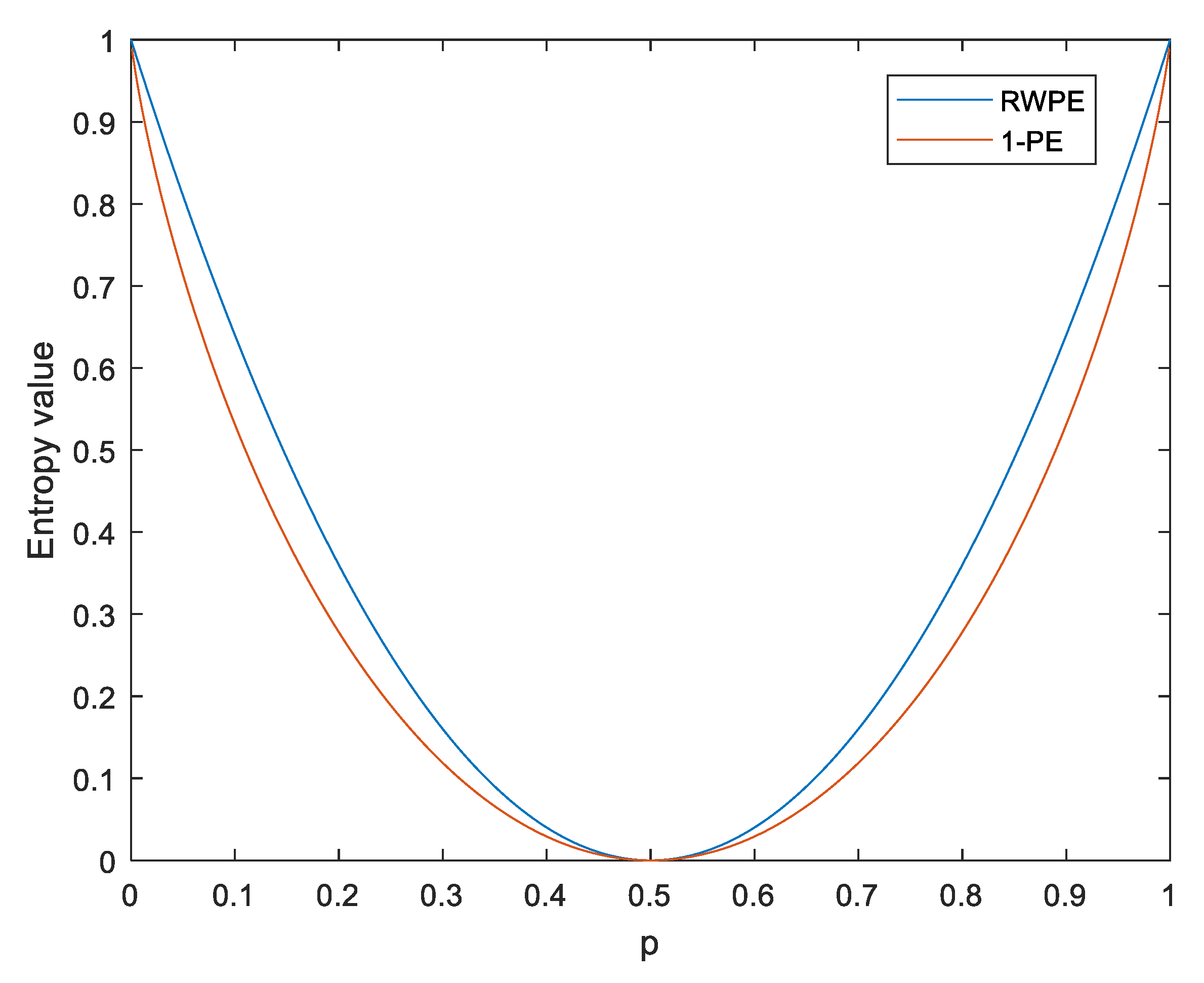
2.1. RWPE
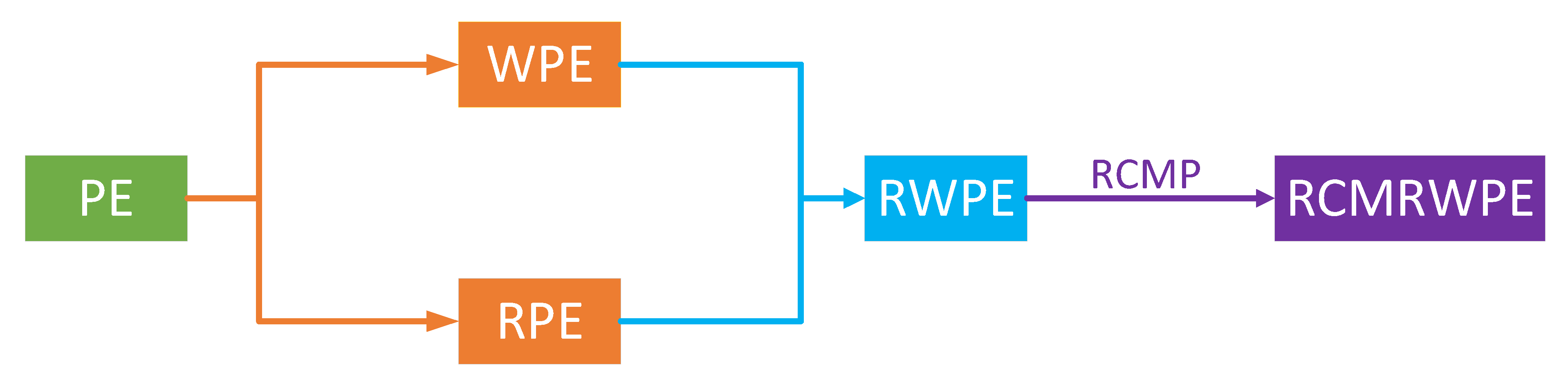
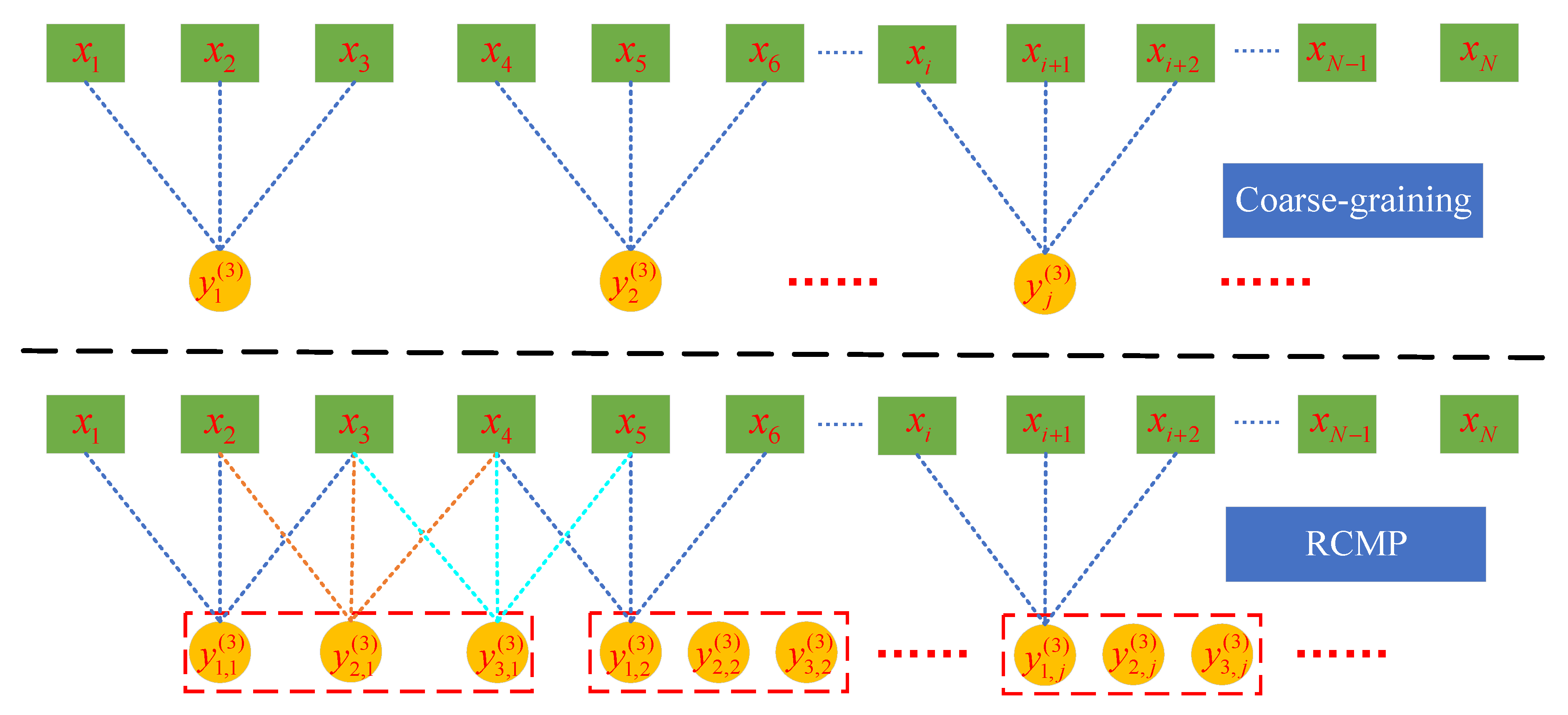
2.2. RCMRWPE
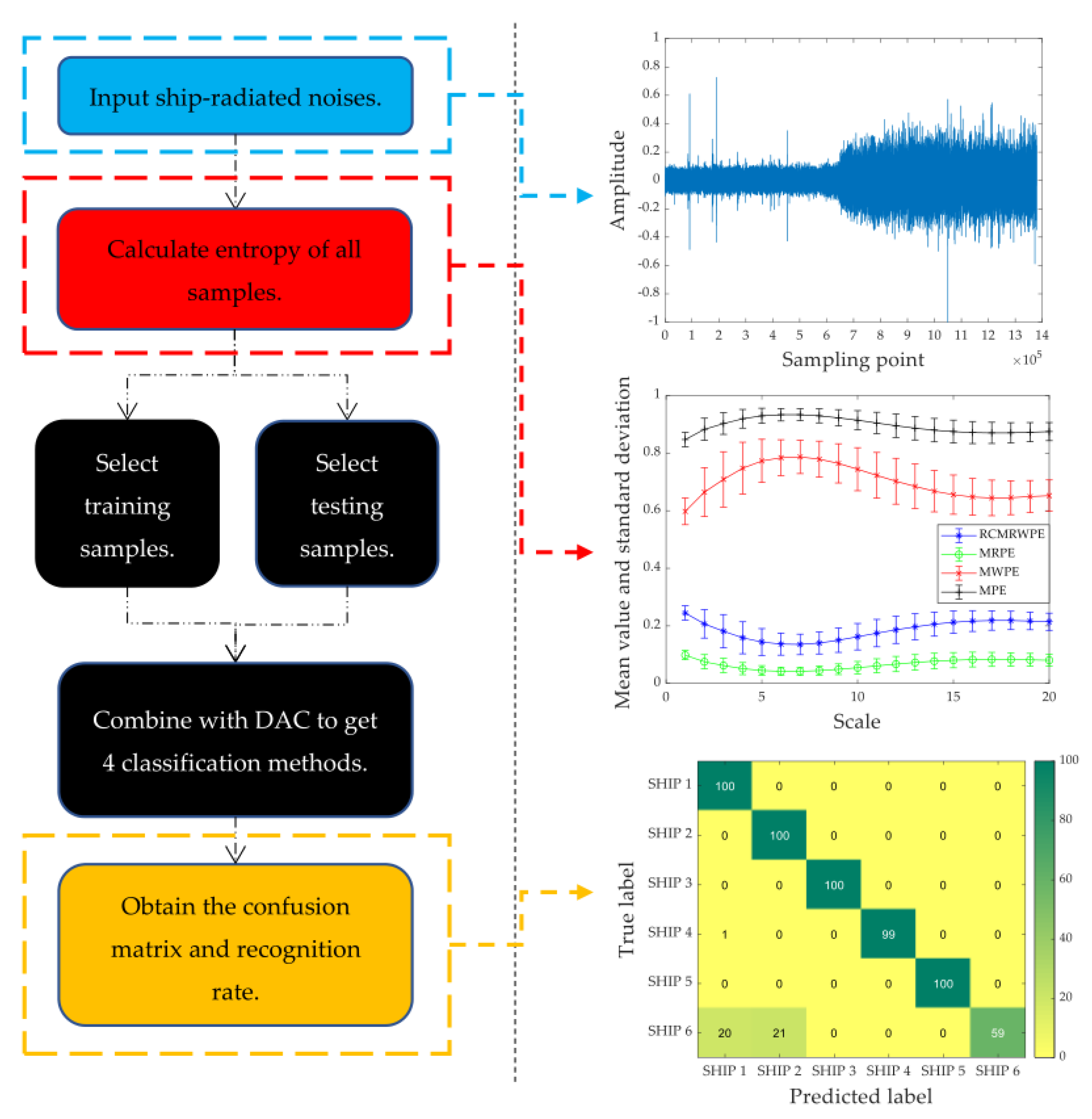
2.3. The Feature Extraction Scheme and Classification Method Based on RCMRWPE
3. A Ship-Radiated Noise Feature Extraction Scheme Based on RCMRWPE
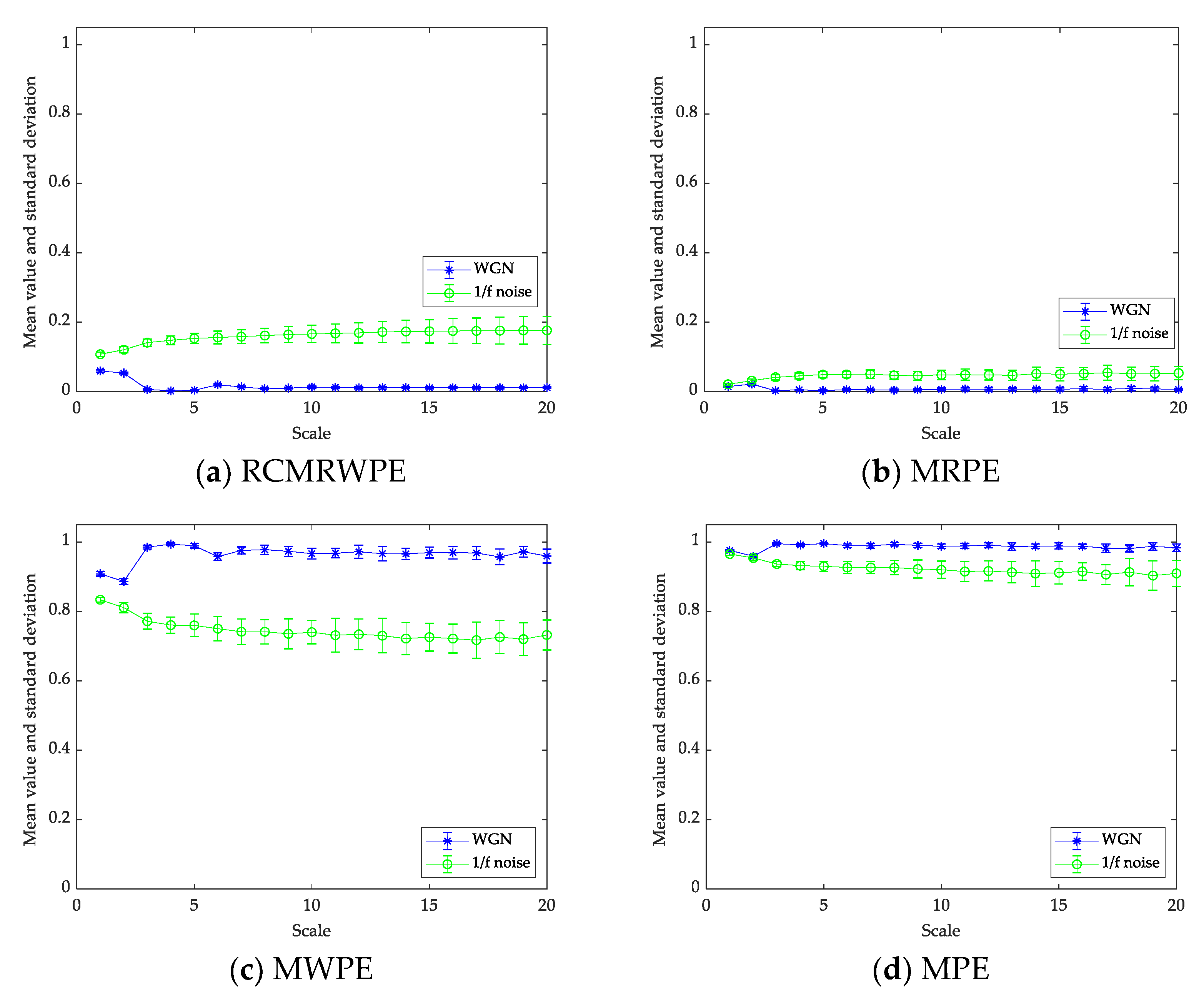
3.1. Synthetic Signals
3.2. Ship-Radiated Noise Datasets
3.2.1. Analysis of Feature Extraction
3.2.2. Analysis of Single Scale
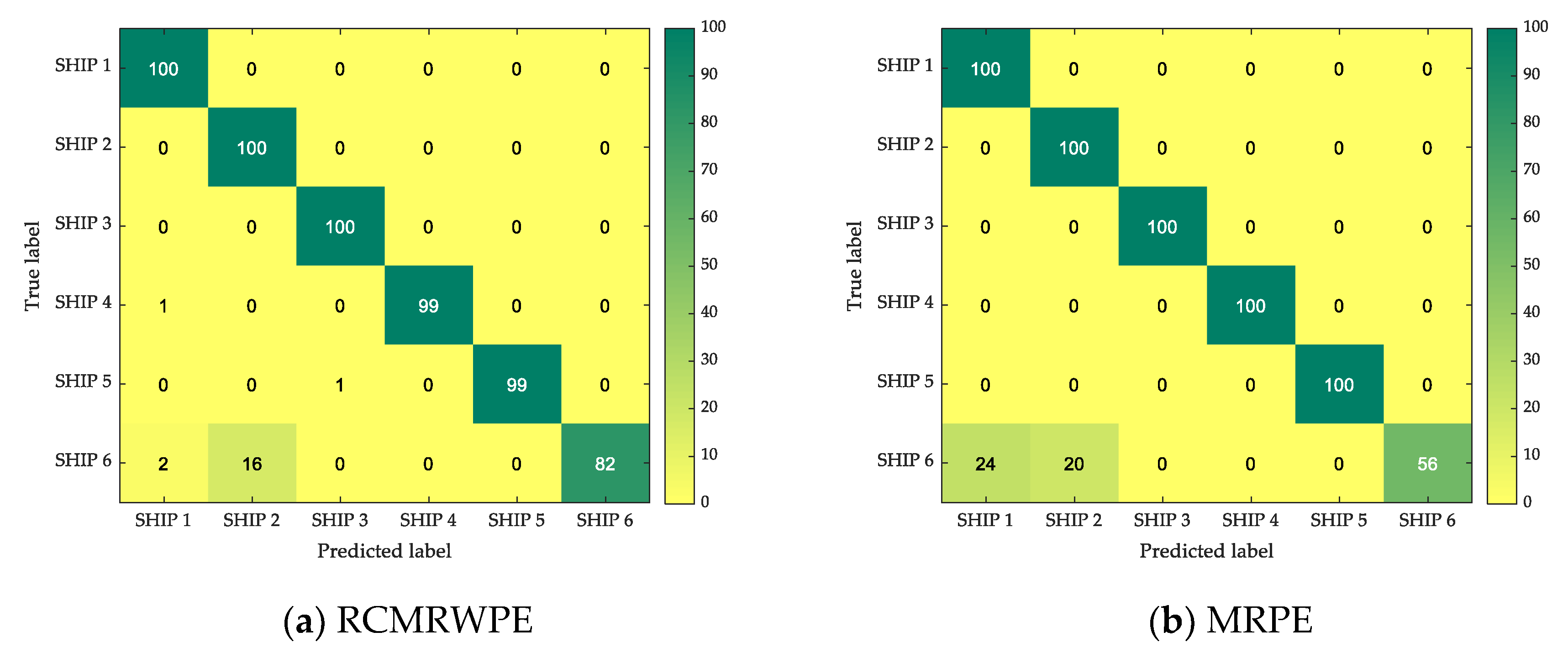
3.2.3. Analysis of Multi-Scale
3.2.4. Analysis of Parameter Selection
4. Conclusions
- (1)
- The feature extraction scheme based on RCMRWPE has smaller variance and better stability than the feature extraction scheme based on MWPE, and MPE.
- (2)
- In the comparative experiment of different classification methods, the RCMRWPE-based classification method shows much better performance than MPE, MWPE, and MRPE-based classification methods under most single scales.
- (3)
- In the multi-scale feature comparison experiment, when the number of selected features exceeds 15, each classification method has a good classification performance. Among them, the classification method based on RCMRWPE has the highest recognition rate, reaching 0.9667, which is 4% higher than the classification method based on MRPE.
- (4)
- The increase of embedding dimension will cause the loss of information in ship-radiated noise, but the RCMRWPE-based classification method still has a good classification performance, which further proves the distinguishing ability and stability of the proposed feature extraction scheme.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olsson, A.; Persson, A.; Bartfai, A.; Boman, I. Sensor technology more than a support. Scand. J. Occup. Ther. 2018, 25, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Guerrero-Ibáñez, J.; Zeadally, S.; Contreras-Castillo, J. Sensor Technologies for Intelligent Transportation Systems. Sensors 2018, 18, 1212. [Google Scholar] [CrossRef] [PubMed]
- Di Bella, A.; Remigi, F. Prediction of noise of moored ships. Proc. Meet. Acoust. 2013, 19, 010053. [Google Scholar]
- Badino, A.; Borelli, D.; Gaggero, T.; Rizzuto, E.; Schenone, C. Acoustical impact of the ship source. In Proceedings of the 21st International Congress on Sound and Vibration, Beijing, China, 13–17 July 2014; pp. 13–17. [Google Scholar]
- Santander, A.; Aspuru, I.; Fernandez, P. OPS Master Plan for Spanish Ports Project. Study of potential acoustic benefits of on-Shore power supply at berth. In Proceedings of the Euronoise 2018, Heraklion, Greece, 27–31 May 2018. [Google Scholar]
- Di Bella, A. Evaluation methods of external airborne noise emissions of moored cruise ships: An overview. In Proceedings of the 21st International Congress on Sound and Vibration, Beijing, China, 6–10 July 2014; pp. 13–17. [Google Scholar]
- Badino, A.; Borelli, D.; Gaggero, T. Noise Emitted from Ships: Impact Inside and Outside the Vessels. Procedia Soc. Behav. Sci. 2012, 48, 868–879. [Google Scholar] [CrossRef]
- Bernardini, M.; Fredianelli, L.; Fidecaro, F.; Gagliardi, P.; Nastasi, M.; Licitra, G. Noise Assessment of Small Vessels for Action Planning in Canal Cities. Environments 2019, 6, 31. [Google Scholar] [CrossRef]
- Fredianelli, L.; Nastasi, M.; Bernardini, M.; Fidecaro, F.; Licitra, G. Pass-by Characterization of Noise Emitted by Different Categories of Seagoing Ships in Ports. Sustainability 2020, 12, 1740. [Google Scholar] [CrossRef]
- Nastasi, M.; Fredianelli, L.; Bernardini, M.; Teti, L.; Fidecaro, F.; Licitra, G. Parameters Affecting Noise Emitted by Ships Moving in Port Areas. Sustainability 2020, 12, 8742. [Google Scholar] [CrossRef]
- Li, Y.; Gao, X.; Wang, L. Reverse Dispersion Entropy: A New Complexity Measure for Sensor Signal. Sensors 2019, 19, 5203. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application to electroencephalogram recordings. Biomed. Signal Process. Control 2016, 23, 28–41. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B.; Zhou, Y. Research on feature extraction of ship-radiated noise based on multi-scale reverse dispersion entropy. Appl. Acoust. 2021, 173, 107737. [Google Scholar] [CrossRef]
- Deng, B.; Cai, L.; Li, S.; Wang, R.; Yu, H.; Chen, Y. Multivariate multi-scale weighted permutation entropy analysis of EEG complexity for Alzheimer’s disease. Cogn. Neurodyn. 2017, 11, 217–231. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Geng, B.; Li, Y. Fluctuation-based reverse dispersion entropy and its applications to signal classification. Appl. Acoust. 2021, 175, 107857. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined Composite Multiscale Dispersion Entropy and its Application to Biomedical Signals. IEEE Trans. Biomed. Eng. 2017, 64, 2872–2879. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2001, 88, 174102. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.; Perez, D.; Rosso, O. Forbidden patterns, permutation entropy and stock market inefficiency. Physica A 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, F.; Gao, J.; Cheng, C.; Song, C. Characterizing Complexity Changes in Chinese Stock Markets by Permutation Entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.A.; Chen, Z.; Chen, X. Feature Extraction of Ship-Radiated Noise Based on Permutation Entropy of the Intrinsic Mode Function with the Highest Energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. A Novel Feature extraction scheme for Ship-Radiated Noise Based on Variational Mode Decomposition and Multi-Scale Permutation Entropy. Entropy 2017, 19, 342. [Google Scholar]
- Fadlallah, B.; Chen, B.; Keil, A.; Principe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Qian, S.; Chang, W.; Xiao, Y.; Cheng, Y. A Novel Bearing Multi-Fault Diagnosis Approach Based on Weighted Permutation Entropy and an Improved SVM Ensemble Classifier. Sensors 2018, 18, 1934. [Google Scholar] [CrossRef]
- Bian, Z.; Ouyang, G.; Li, Z.; Li, Q.; Wang, L.; Li, X. Weighted-Permutation Entropy Analysis of Resting State EEG from Diabetics with Amnestic Mild Cognitive Impairment. Entropy 2016, 18, 307. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Li, X.; Yang, X. A Novel Linear Spectrum Frequency Feature Extraction Technique for Warship Radio Noise Based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, Duffing Chaotic Oscillator, and Weighted-Permutation Entropy. Entropy 2019, 21, 507. [Google Scholar] [CrossRef]
- Bandt, C. A New Kind of Permutation Entropy Used to Classify Sleep Stages from Invisible EEG Microstructure. Entropy 2017, 19, 197. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Yu, J.; Yang, X. A Fusion Frequency Feature extraction scheme for Underwater Acoustic Signal Based on Variational Mode Decomposition, Duffing Chaotic Oscillator and a Kind of Permutation Entropy. Electronics 2019, 8, 61. [Google Scholar] [CrossRef]
- Li, Y. Reverse Weighted-Permutation Entropy: A Novel Complexity Metric Incorporating Distance and Amplitude Information. Proceedings 2020, 46, 1. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H. Use of generalized refined composite multiscale fractional dispersion entropy to diagnose the faults of rolling bearing. Nonlinear Dyn. 2020, 101, 1417–1440. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Feature extraction of ship-radiated noise based on VMD and center frequency. J. Vib. Shock 2018, 37, 213–218. [Google Scholar]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. A Hybrid Energy Feature Extraction Approach for Ship-Radiated Noise Based on CEEMDAN Combined with Energy Difference and Energy Entropy. Processes 2019, 7, 69. [Google Scholar] [CrossRef]


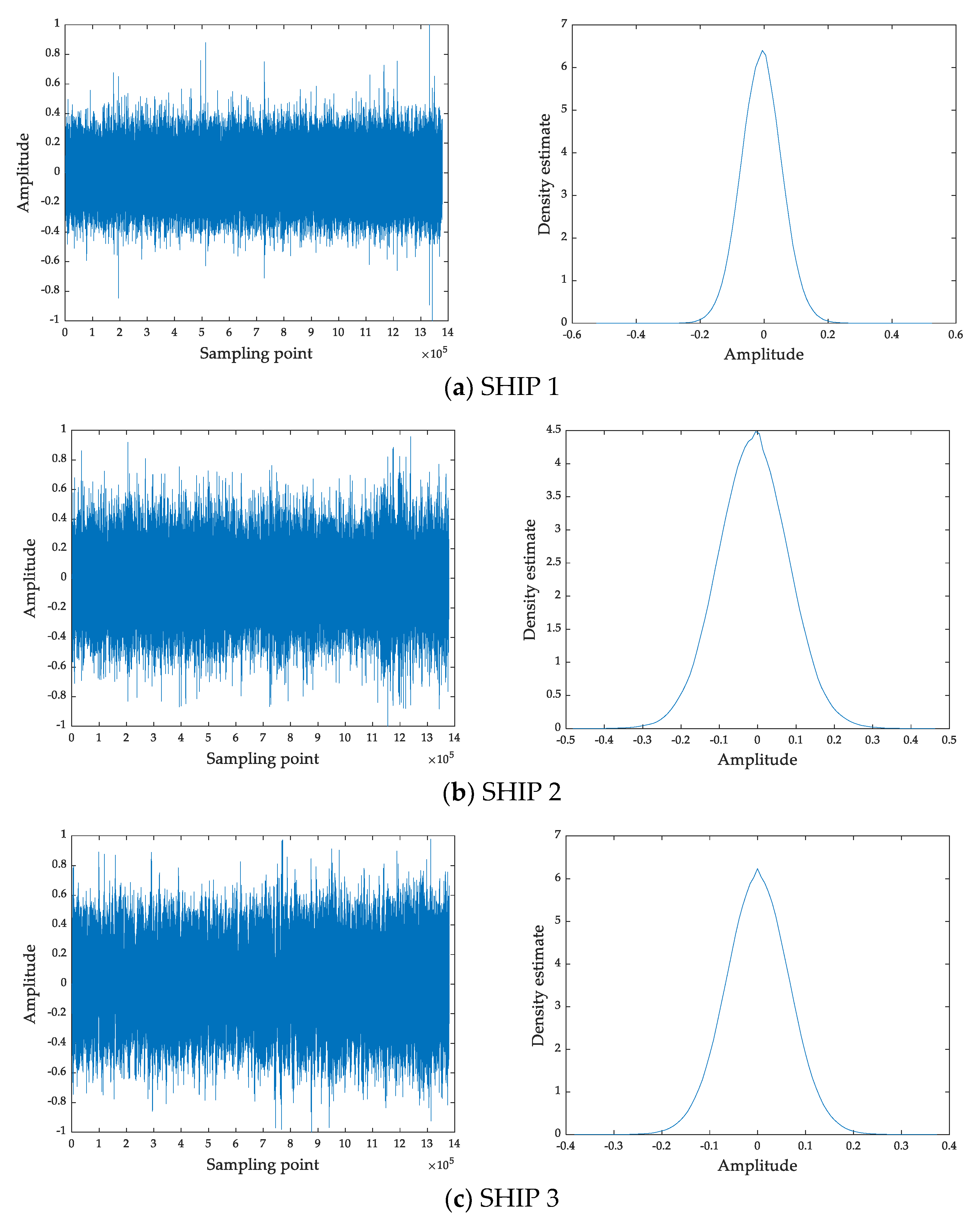
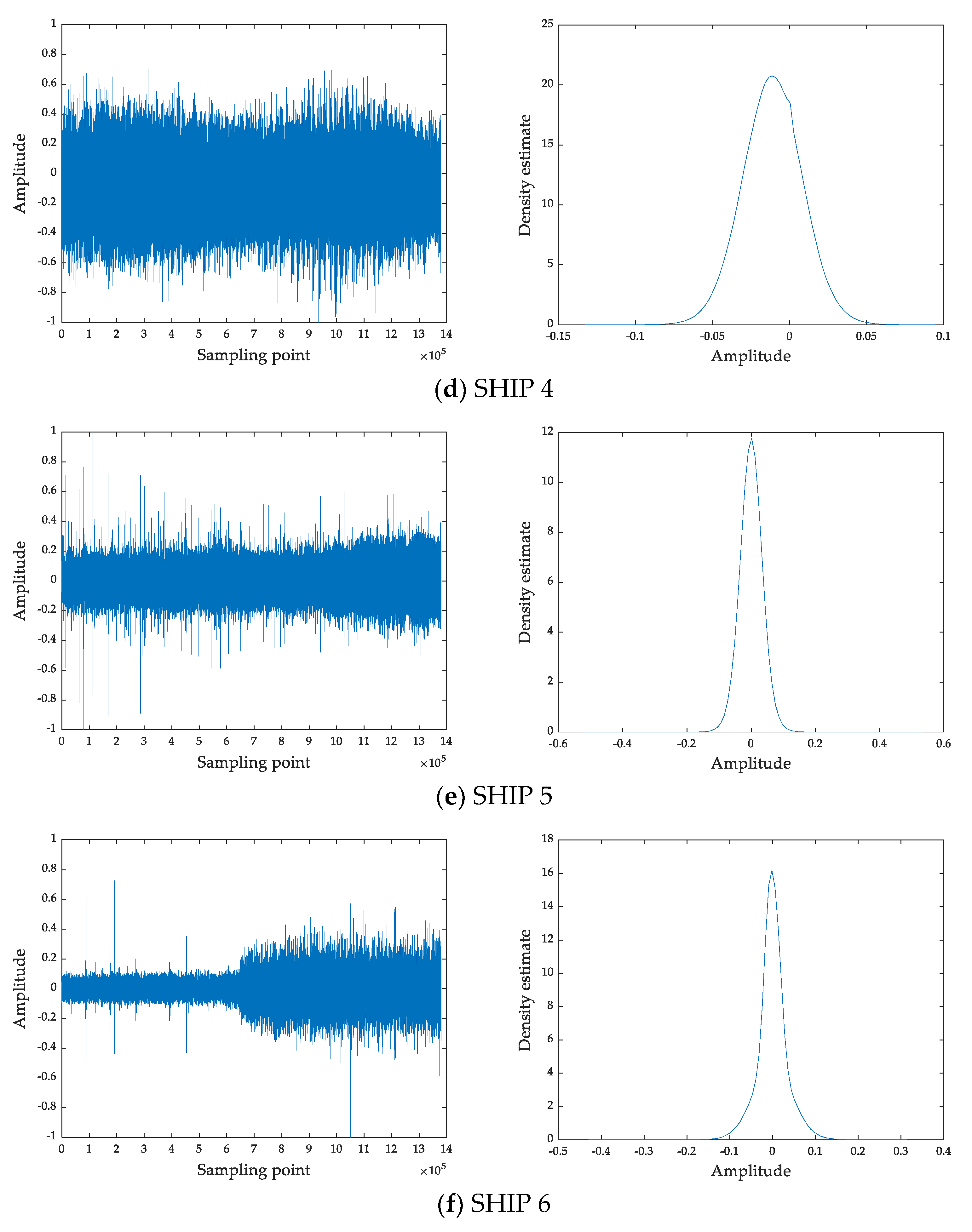



| Ship-Radiated Noise Class | Used Data |
|---|---|
| SHIP 1 | State Ferry |
| SHIP 2 | Cruise Ship |
| SHIP 3 | Freighter |
| SHIP 4 | Small Diesel Engine |
| SHIP 5 | Motorboat |
| SHIP 6 | Ocean Liner |
| Number of Features | Recognition Rate | |||
|---|---|---|---|---|
| RCMRWPE | MRPE | MWPE | MPE | |
| 1 | 0.7467 | 0.7267 | 0.7300 | 0.7250 |
| 2 | 0.7733 | 0.8333 | 0.7767 | 0.8317 |
| 3 | 0.8300 | 0.8783 | 0.8317 | 0.8783 |
| 4 | 0.8333 | 0.8833 | 0.8283 | 0.8883 |
| 5 | 0.8300 | 0.8850 | 0.8317 | 0.8850 |
| 6 | 0.8300 | 0.8817 | 0.8317 | 0.8817 |
| 7 | 0.8317 | 0.8783 | 0.8267 | 0.8783 |
| 8 | 0.8333 | 0.8800 | 0.8267 | 0.8800 |
| 9 | 0.8333 | 0.8767 | 0.8317 | 0.8750 |
| 10 | 0.8333 | 0.8783 | 0.8283 | 0.8750 |
| 11 | 0.8400 | 0.8683 | 0.8283 | 0.8683 |
| 12 | 0.8667 | 0.8833 | 0.8300 | 0.8833 |
| 13 | 0.9533 | 0.8950 | 0.8567 | 0.8950 |
| 14 | 0.9650 | 0.9100 | 0.8933 | 0.9100 |
| 15 | 0.9617 | 0.9167 | 0.9383 | 0.9150 |
| 16 | 0.9650 | 0.9217 | 0.9433 | 0.9250 |
| 17 | 0.9667 | 0.9250 | 0.9450 | 0.9300 |
| 18 | 0.9600 | 0.9250 | 0.9367 | 0.9300 |
| 19 | 0.9617 | 0.9250 | 0.9367 | 0.9300 |
| 20 | 0.9600 | 0.9267 | 0.9367 | 0.9317 |
| Number of Features | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|
| Recognition Rate ( = 4) | RCMRWPE | 0.9650 | 0.9650 | 0.9617 | 0.9633 | 0.9633 |
| MRPE | 0.9183 | 0.9200 | 0.9200 | 0.9217 | 0.9167 | |
| MWPE | 0.9350 | 0.9367 | 0.9367 | 0.9383 | 0.9383 | |
| MPE | 0.8483 | 0.8483 | 0.8450 | 0.8500 | 0.8550 | |
| Recognition Rate ( = 5) | RCMRWPE | 0.9217 | 0.9233 | 0.9200 | 0.9233 | 0.9250 |
| MRPE | 0.9017 | 0.9017 | 0.9017 | 0.9017 | 0.8967 | |
| MWPE | 0.9050 | 0.9067 | 0.9083 | 0.9100 | 0.9083 | |
| MPE | 0.8433 | 0.8417 | 0.8433 | 0.8400 | 0.8400 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Geng, B.; Jiao, S. Refined Composite Multi-Scale Reverse Weighted Permutation Entropy and Its Applications in Ship-Radiated Noise. Entropy 2021, 23, 476. https://doi.org/10.3390/e23040476
Li Y, Geng B, Jiao S. Refined Composite Multi-Scale Reverse Weighted Permutation Entropy and Its Applications in Ship-Radiated Noise. Entropy. 2021; 23(4):476. https://doi.org/10.3390/e23040476
Chicago/Turabian StyleLi, Yuxing, Bo Geng, and Shangbin Jiao. 2021. "Refined Composite Multi-Scale Reverse Weighted Permutation Entropy and Its Applications in Ship-Radiated Noise" Entropy 23, no. 4: 476. https://doi.org/10.3390/e23040476
APA StyleLi, Y., Geng, B., & Jiao, S. (2021). Refined Composite Multi-Scale Reverse Weighted Permutation Entropy and Its Applications in Ship-Radiated Noise. Entropy, 23(4), 476. https://doi.org/10.3390/e23040476







