Excitation Functions of Tsallis-Like Parameters in High-Energy Nucleus–Nucleus Collisions
Abstract
1. Introduction
2. Formalism and Method
3. Results and Discussion
3.1. Comparison with Data and Tendencies of Free Parameters
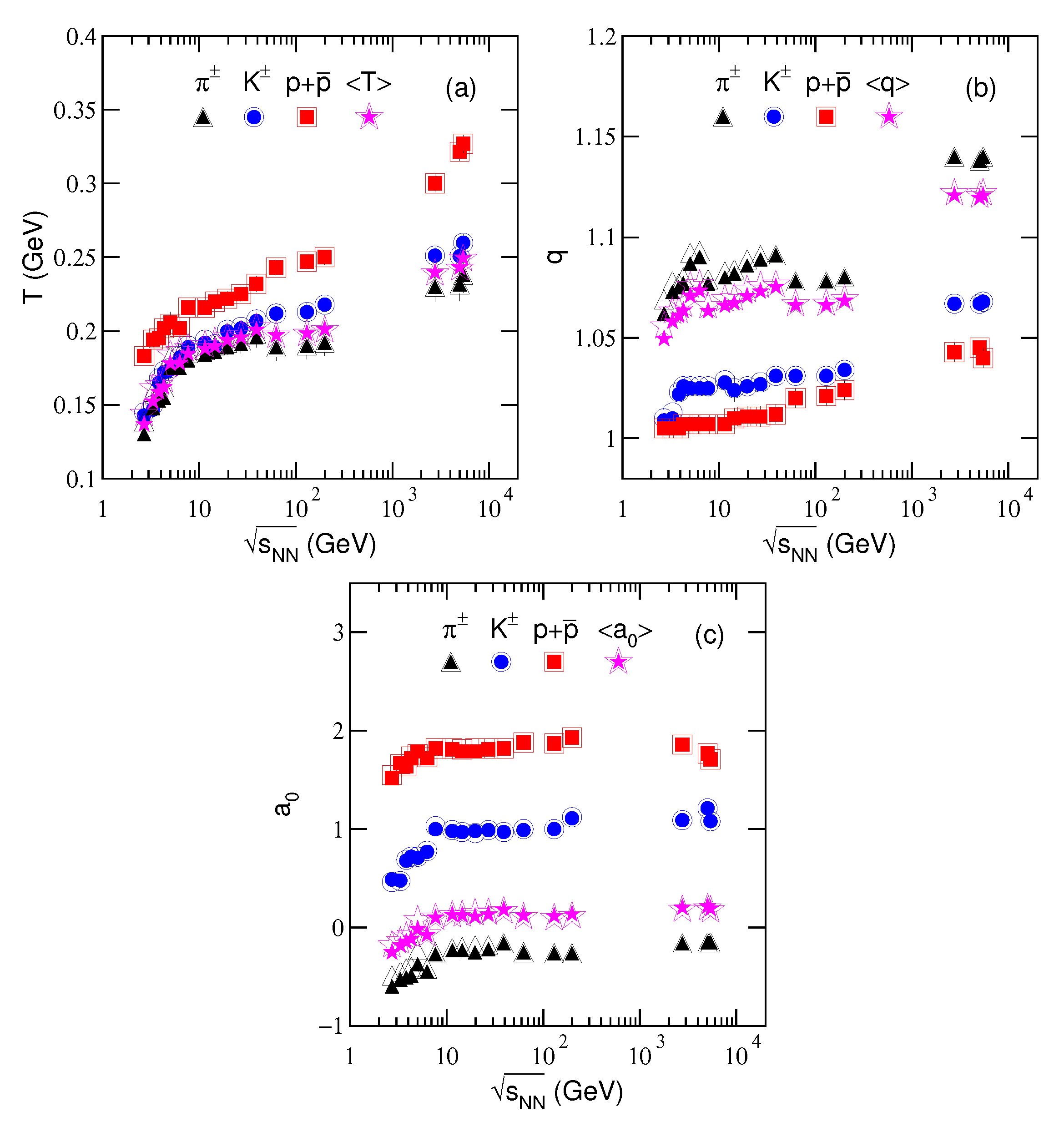
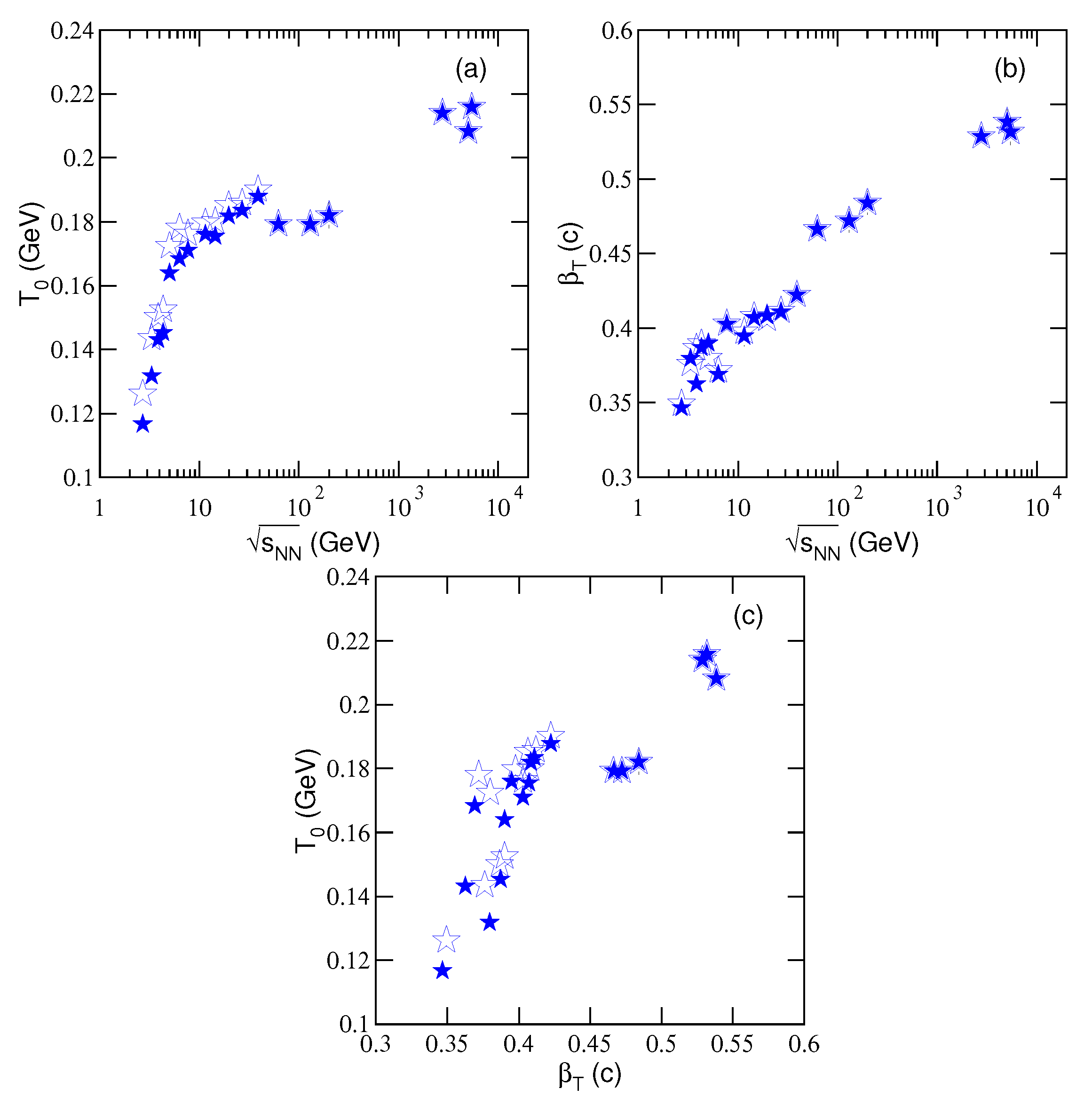
3.2. Derived Parameters and Their Tendencies
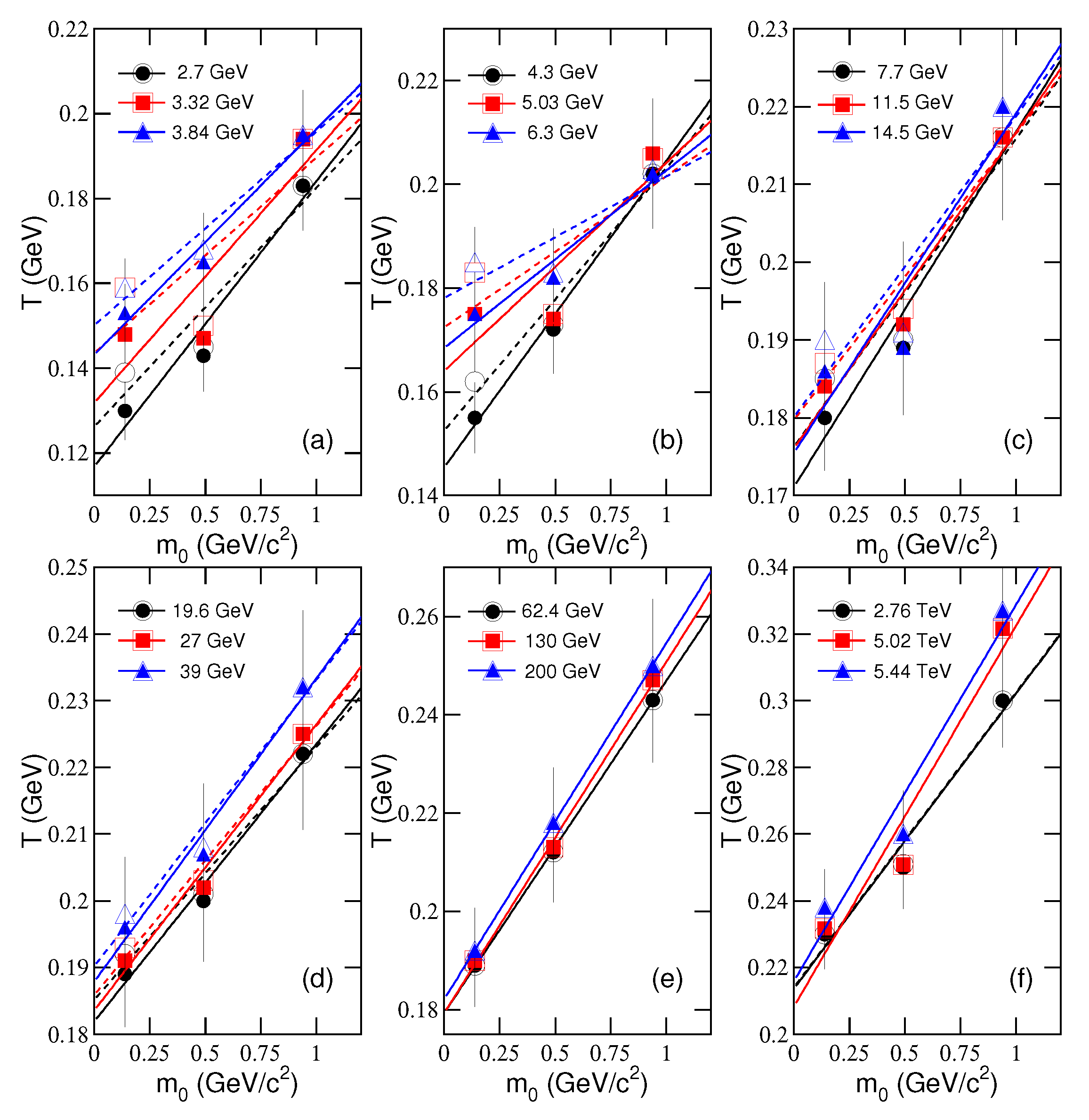
3.3. Further Discussion
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khuntia, A.; Tripathy, S.; Shahoo, R.; Cleymans, J. Multiplicity dependence of non-extensive parameters for strange and multi-strange particles in proton-proton collisions at TeV at the LHC. Eur. Phys. J. A 2017, 53, 103. [Google Scholar] [CrossRef]
- Ahmad, S.; Ahmad, A.; Chandra, A.; Zafar, M.; Irfan, M. Entropy analysis in relativistic heavy-ion collisions. Adv. High Energy Phys. 2013, 2013, 836071. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly relativistic nucleus-nucleus collisions: The central rapidity region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Dusling, K. From initial-state fluctuations to final-state observables. Nucl. Phys. A 2013, 904–905, 59c–66c. [Google Scholar] [CrossRef]
- Gyulassy, M.; Mclerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 2005, 750, 30–63. [Google Scholar] [CrossRef]
- Tawfik, A.N. Equilibrium statistical-thermal models in high-energy physics. Int. J. Mod. Phys. A 2014, 29, 1430021. [Google Scholar] [CrossRef]
- Gupta, S.; Luo, X.F.; Mohanty, B.; Ritter, H.G.; Xu, N. Scale for the phase diagram of quantum chromodynamics. Science 2011, 332, 1525–1528. [Google Scholar] [CrossRef]
- Xu, N. for the STAR Collaboration. An overview of STAR experimental results. Nucl. Phys. A 2014, 931, 1–12. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Luo, X.F.; Xu, N. Search for the QCD critical point with fluctuations of conserved quantities in relativistic heavy-ion collisions at RHIC: An overview. Nucl. Sci. Tech 2017, 28, 112. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Yassin, H.; Abo Elyazeed, E.R. Extensive/nonextensive statistics for pT distributions of various charged particles produced in p+p and A+A collisions in a wide range of energies. arXiv 2019, arXiv:1905.12756. [Google Scholar]
- Tawfik, A.N. Analogy of QCD hadronization and Hawking-Unruh radiation at NICA. Eur. Phys. J. A 2016, 52, 254. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Yassin, H.; Abo Elyazeed, E.R. Chemical freezeout parameters within generic nonextensive statistics. Indian J. Phys. 2018, 92, 1325–1335. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Biswas, D.; Ghosh, S.K.; Ray, R.; Singha, P. Novel scheme for parametrizing the chemical freeze-out surface in heavy ion collision experiments. Phys. Rev. D 2019, 100, 054037. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Biswas, D.; Ghosh, S.K.; Ray, R.; Singha, P. Systematics of chemical freeze-out parameters in heavy-ion collision experiments. Phys. Rev. D 2020, 101, 054002. [Google Scholar] [CrossRef]
- Biswas, D. Centrality dependence of chemical freeze-out parameters and strangeness equilibration in RHIC and LHC. arXiv 2020, arXiv:2003.10425. [Google Scholar]
- Schnedermann, E.; Sollfrank, J.; Heinz, U. Thermal phenomenology of hadrons from 200A GeV S+S collisions. Phys. Rev. C 1993, 48, 2462–2475. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Identified particle production, azimuthal anisotropy, and interferometry measurements in Au+Au collisions at = 9.2 GeV. Phys. Rev. C 2010, 81, 024911. [Google Scholar] [CrossRef]
- Tang, Z.B.; Xu, Y.C.; Ruan, L.J.; Van Buren, G.; Wang, F.Q.; Xu, Z.B. Spectra and radial flow in relativistic heavy ion collisions with Tsallis statistics in a blast-wave description. Phys. Rev. C 2009, 79, 051901(R). [Google Scholar] [CrossRef]
- Tang, Z.B.; Yi, L.; Ruan, L.J.; Shao, M.; Chen, H.F.; Li, C.; Mohanty, B.; Sorensen, P.; Tang, A.H.; Xu, Z.B. Statistical origin of constituent-quark scaling in the QGP hadronization. Chin. Phys. Lett. 2013, 30, 031201. [Google Scholar] [CrossRef][Green Version]
- Jiang, K.; Zhu, Y.Y.; Liu, W.T.; Chen, H.F.; Li, C.; Ruan, L.J.; Tang, Z.B.; Xu, Z.B. Onset of radial flow in p+p collisions. Chin. Phys. Lett. 2015, 91, 024910. [Google Scholar]
- Heiselberg, H.; Levy, A.M. Elliptic flow and Hanbury-Brown-Twiss correlations in noncentral nuclear collisions. Phys. Rev. C 1999, 59, 2716–2727. [Google Scholar] [CrossRef]
- Takeuchi, S.; Murase, K.; Hirano, T.; Huovinen, P.; Nara, Y. Effects of hadronic rescattering on multistrange hadrons in high-energy nuclear collisions. Phys. Rev. C 2015, 92, 044907. [Google Scholar] [CrossRef]
- Wei, H.-R.; Liu, F.-H.; Lacey, R.A. Kinetic freeze-out temperature and flow velocity extracted from transverse momentum spectra of final-state light flavor particles produced in collisions at RHIC and LHC. Eur. Phys. J. A 2016, 52, 102. [Google Scholar] [CrossRef]
- Wei, H.-R.; Liu, F.-H.; Lacey, R.A. Disentangling random thermal motion of particles and collective expansion of source from transverse momentum spectra in high energy collisions. J. Phys. G 2016, 43, 125102. [Google Scholar] [CrossRef]
- Lao, H.-L.; Wei, H.-R.; Liu, F.-H.; Lacey, R.A. An evidence of mass-dependent differential kinetic freeze-out scenario observed in Pb-Pb collisions at 2.76 TeV. Eur. Phys. J. A 2016, 52, 203. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, F.-H. Energy dependent kinetic freeze-out temperature and transverse flow velocity in high energy collisions. Eur. Phys. J. A 2018, 54, 169. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, F.-H.; Waqas, M.; Al-Yusufi, R.; Mujear, A. Excitation functions of related parameters from transverse momentum (mass) spectra in high energy collisions. Adv. High Energy Phys. 2020, 2020, 5356705. [Google Scholar] [CrossRef]
- Zheng, H.; Zhu, L.L. Comparing the Tsallis distribution with and without thermodynamical description in p+p collisions. Adv. High Energy Phys. 2016, 2016, 9632126. [Google Scholar] [CrossRef]
- Liu, F.-H.; Gao, Y.-Q.; Tian, T.; Li, B.-C. Unified description of transverse momentum spectrums contributed by soft and hard processes in high-energy nuclear collisions. Eur. Phys. J. A 2014, 50, 94. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.D.; Beavis, D.; Budick, B.; Chang, J.; Chasman, C.; Chen, Z.; Chu, Y.Y.; et al. Excitation function of K+ and π+ production in Au+Au reactions at 2–10A GeV. Phys. Lett. B 2000, 476, 1–8. [Google Scholar] [CrossRef]
- Klay, J.L.; Ajitanand, N.N.; Alexander, J.M.; Anderson, M.G.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.L.; et al. Longitudinal flow from (2–8)A GeV central Au+Au collisions. Phys. Rev. Lett. 2002, 88, 102301. [Google Scholar] [CrossRef] [PubMed]
- Klay, J.L.; Ajitanand, N.N.; Alexander, J.M.; Anderson, M.G.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.L.; et al. Charged pion production in 2A to 8A GeV central Au+Au Collisions. Phys. Rev. C 2003, 68, 054905. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.D.; Beavis, D.; Britt, H.C.; Chang, J.; Chasman, C.; Chen, Z.; Chi, C.Y.; et al. Kaon production in Au+Au collisions at 11.6 A GeV/c. Phys. Rev. C 1998, 58, 3523–3538. [Google Scholar] [CrossRef]
- Ahle, L.; Akiba, Y.; Ashktorab, K.; Baker, M.D.; Beavis, D.; Britt, H.C.; Chang, J.; Chasman, C.; Chen, Z.; Chi, C.Y.; et al. Particle production at high baryon density in central Au+Au reactions at 11.6A GeV/c. Phys. Rev. C 1998, 57, R466–R470. [Google Scholar] [CrossRef]
- Alt, C.; Anticic, T.; Baatar, B.; Barna, D.; Bartke, J.; Betev, L.; Białkowska, H.; Blume, C.; Boimska, B.; Botje, M.; et al. Pion and kaon production in central Pb+Pb collisions at 20A and 30A GeV: Evidence for the onset of deconfinement. Phys. Rev. C 2008, 77, 024903. [Google Scholar] [CrossRef]
- Afanasiev, S.V.; Anticic, T.; Barna, D.; Bartke, J.; Barton, R.A.; Behler, M.; Betev, L.; Białkowska, H.; Billmeier, A.; Blume, C.; et al. Energy dependence of pion and kaon production in central Pb+Pb collisions. Phys. Rev. C 2002, 66, 054902. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; Aparin, A.; et al. Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Bairathi, V. For the STAR Collaboration. Study of the bulk properties of the system formed in Au+Au collisions at = 14.5 GeV using the STAR detector at RHIC. Nucl. Phys. A 2016, 956, 292–295. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Systematic measurements of identified particle spectra in pp, d+Au, and Au+Au collisions at the STAR detector. Phys. Rev. C 2009, 79, 034909. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Centrality dependence of π, K, and p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- Vázquez, O. New results on collectivity with ALICE. Proceedings for a Parallel Session Talk at the Fifth Annual Large Hadron Collider Physics Conference, May 15–20, 2017. arXiv 2017, arXiv:1710.04715. [Google Scholar]
- Ragoni, S. Production of pions, kaons and protons in Xe-Xe collisions at = 5.44 TeV. PoS 2018, LHCP2018, 085. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Biró, T.S.; Purcsel, G.; Ürmössy, K. Non-extensive approach to quark matter. Eur. Phys. J. A 2009, 40, 325–340. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic thermodynamics: Transverse momentum distributions in high-energy physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Cleymans, J.; Paradza, M.W. Tsallis statistics in high energy physics: Chemical and thermal freeze-outs. Physics 2020, 2, 654–664. [Google Scholar] [CrossRef]
- Yang, P.-P.; Liu, F.-H.; Sahoo, R. A new description of transverse momentum spectra of identified particles produced in proton-proton collisions at high energies. Adv. High Energy Phys. 2020, 2020, 6742578. [Google Scholar] [CrossRef]
- Yang, P.-P.; Duan, M.-Y.; Liu, F.-H. Dependence of related parameters on centrality and mass in a new treatment for transverse momentum spectra in high energy collisions. Eur. Phys. J. A 2021, 57, 63. [Google Scholar] [CrossRef]
- Yang, P.-P.; Wang, Q.; Liu, F.-H. Mutual derivation between arbitrary distribution forms of momenta and momentum components. Int. J. Theor. Phys. 2019, 58, 2603–2618. [Google Scholar] [CrossRef]
- Zhou, G.-R. Probability Theory and Mathamatic and Physics Statsitics; Higher Education Press: Beijing, China, 1984. [Google Scholar]
- Braun-Munzinger, P.; Wambach, J. Colloquium: Phase diagram of strongly interacting matter. Rev. Mod. Phys. 2009, 81, 1031–1050. [Google Scholar] [CrossRef]
- Cleymans, J.; Oeschler, H.; Redlich, K.; Wheaton, S. Comparison of chemical freeze-out criteria in heavy-ion collisions. Phys. Rev. C 2006, 73, 034905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P. Ultrarelativistic nucleus-nucleus collisions and the quark-gluon plasma. In Proceedings of the 8th Hispalensis International Summer School on Exotic Nuclear Physics: The Hispalensis Lectures on Nuclear Physics, Seville, Spain, 9–21 June 2003; Volume 2, pp. 35–67. [Google Scholar]
- Rozynek, J.; Wilk, G. Nonextensive effects in the Nambu-Jona-Lasinio model of QCD. J. Phys. G 2009, 36, 125108. [Google Scholar] [CrossRef]
- Rozynek, J.; Wilk, G. Nonextensive Nambu-Jona-Lasinio model of QCD matter. Eur. Phys. J. A 2016, 52, 13. [Google Scholar] [CrossRef]
- Shen, K.M.; Zhang, H.; Hou, D.F.; Zhang, B.W.; Wang, E.K. Chiral phase transition in linear sigma model with nonextensive statistical mechanics. Adv. High Energy Phys. 2017, 2017, 4135329. [Google Scholar] [CrossRef]
- Zhao, Y.P. Th8ermodynamic properties and transport coefficients of QCD matter within the nonextensive Polyako-Nambu-Jona-Lasinio model. Phys. Rev. D 2020, 101, 096006. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions. Acta Phys. Pol. B 2009, 40, 1005–1012. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. The horn, the hadron mass spectrum and the QCD phase diagram: The statistical model of hadron production in central nucleus-nucleus collisions. Nucl. Phys. A 2010, 834, 237c–240c. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Hadron production in central nucleus-nucleus collisions at chemical freeze-out. Nucl. Phys. A 2006, 772, 167–199. [Google Scholar] [CrossRef]
- Zhang, H.-X.; Shan, P.-J. Statistical simulation method for determinating the errors of fit parameters. In Proceedings of the 8th National Conferences on Nuclear Physiscs (Volume II), Xi’an, China, 3–7 December 1991; (In Chinese). Available online: http://cpfd.cnki.com.cn/Article/CPFDTOTAL-HWLX199112002128.htm (accessed on 1 March 2021).
- Avdyushev, V.A. A new method for the statistical simulation of the virtual values of parameters in inverse orbital dynamics problems. Sol. Syst. Res. 2009, 43, 543–551. [Google Scholar] [CrossRef]
- Biró, T.S.; Ürmössy, K. Pions and kaons from stringy quark matter. J. Phys. G 2009, 36, 064044. [Google Scholar] [CrossRef]
- Csanád, M.; Vargyas, M. Observables from a solution of (1+3)-dimensional relativistic hydrodynamics. Eur. Phys. J. A 2010, 44, 473–478. [Google Scholar] [CrossRef]
- Ürmössy, K.; Biró, T.S. Cooper-Frye formula and non-extensive coalescence at RHIC energy. Phys. Lett. B 2010, 689, 14–17. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.-H.; Wang, R.-Q.; Siddique, I. Energy scan/dependence of kinetic freeze-out scenarios of multi-strange and other identified particles in central nucleus-nucleus collisions. Eur. Phys. J. A 2020, 56, 188. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, F.-H. Kinetic freeze-out properties from transverse momentum spectra of pions in high energy proton-proton collisions. Physics 2020, 2, 277–308. [Google Scholar] [CrossRef]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; Averbeck, R.; et al. Identified charged particle spectra and yields in Au+Au collisions at = 200 GeV. Phys. Rev. C 2004, 69, 034909. [Google Scholar] [CrossRef]
- Csörgo, T.; Lörstad, B. Bose-Einstein correlations for three-dimensionally expanding, cylindrically symmetric, finite systems. Phys. Rev. C 1996, 54, 1390–1403. [Google Scholar] [CrossRef]
- Csörgo, T.; Akkelin, S.V.; Hama, Y.; Lukács, B.; Sinyukov, Y.M. Observables and initial conditions for selfsimilar ellipsoidal flows. Phys. Rev. C 2003, 67, 034904. [Google Scholar] [CrossRef]
- Csanád, M.; Csörgo, T.; Lörstad, B. Buda-Lund hydro model for ellipsoidally symmetric fireballs and the elliptic flow at RHIC. Nucl. Phys. A 2004, 742, 80–94. [Google Scholar] [CrossRef]
- Lao, H.-L.; Liu, F.-H.; Li, B.-C.; Duan, M.-Y. Kinetic freeze-out temperatures in central and peripheral collisions: Which one is larger? Nucl. Sci. Tech. 2018, 29, 82. [Google Scholar] [CrossRef]
- Lao, H.-L.; Liu, F.-H.; Li, B.-C.; Duan, M.-Y.; Lacey, R.A. Examining the model dependence of the determination of kinetic freeze-out temperature and transverse flow velocity in small collision system. Nucl. Sci. Tech. 2018, 29, 164. [Google Scholar] [CrossRef]
- Cleymans, J. The physics case for the ≈ 10 GeV energy region. in Walter Greiner Memorial Volume, edited by P. O. Hess (World Scientiflc, Singapore) (2018). arXiv 2017, arXiv:1711.02882. [Google Scholar]
- Biró, T.S.; Zimányi, J. Quarkochemistry in relativistic heavy ion collisions. Phys. Lett. B 1982, 113, 6–10. [Google Scholar] [CrossRef]
- Biró, T.S.; Zimányi, J. Quark-gluon plasma formation in heavy ion collisions and quarkochemistry. Nucl. Phys. A 1983, 395, 525–538. [Google Scholar] [CrossRef]
- Biró, T.S.; Lévai, P.; Zimányi, J. ALCOR: A dynamic model for hadronization. Phys. Lett. B 1995, 347, 6–12. [Google Scholar] [CrossRef]
- Zimányi, J.; Biró, T.S.; Csörgö, T.; Lévai, P. Particle spectra from the ALCOR model. Heavy Ion Phys. 1996, 4, 15–32. [Google Scholar]
- Biró, T.S.; Lévai, P.; Zimányi, J. Quark coalescence in the mid-rapidity region at RHIC. J. Phys. G 2002, 28, 1561–1566. [Google Scholar]
- Werner, K. Core-corona separation in ultra-relativistic heavy ion collisions. Phys. Rev. Lett. 2007, 98, 152301. [Google Scholar] [CrossRef] [PubMed]
- Aichelin, J.; Werner, K. Core-corona model describes the centrality dependence of v2/ϵ. J. Phys. G 2010, 37, 94006. [Google Scholar] [CrossRef][Green Version]
- Schreiber, C.; Werner, K.; Aichelin, J. Identified particle spectra for Au+Au collisions at = 200 GeV from STAR, PHENIX and BRAHMS in comparison to core-corona model predictions. Proceedings to the Workshop on Dense Matter—DM 2010, Stellenbosch, South Africa, April 2010. arXiv 2010, arXiv:1012.2066. [Google Scholar]
- Petrovici, M.; Berceanu, I.; Pop, A.; Târzilaˇ, M.; Andrei, C. Core-corona interplay in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2017, 96, 014908. [Google Scholar] [CrossRef]
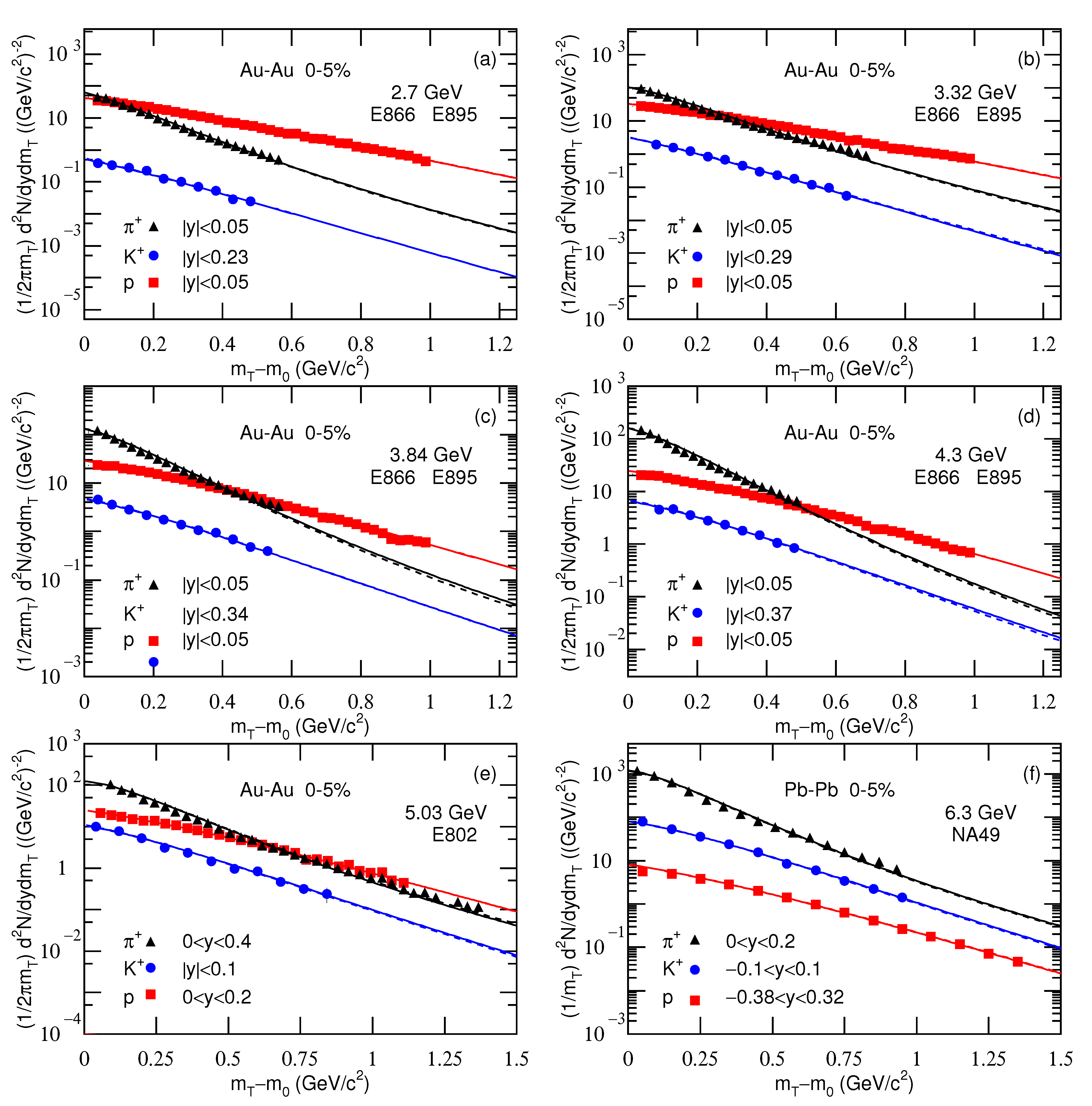
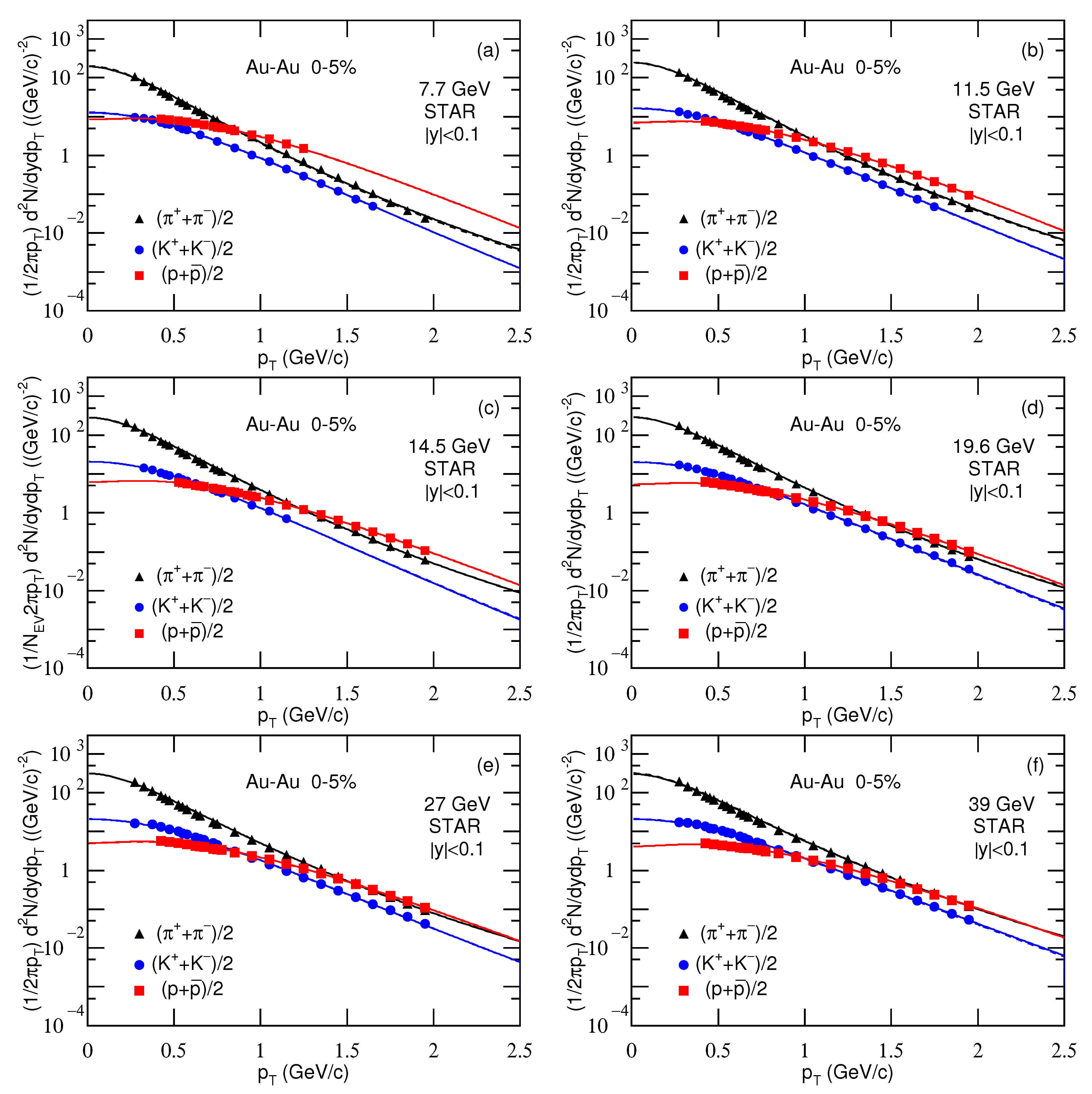

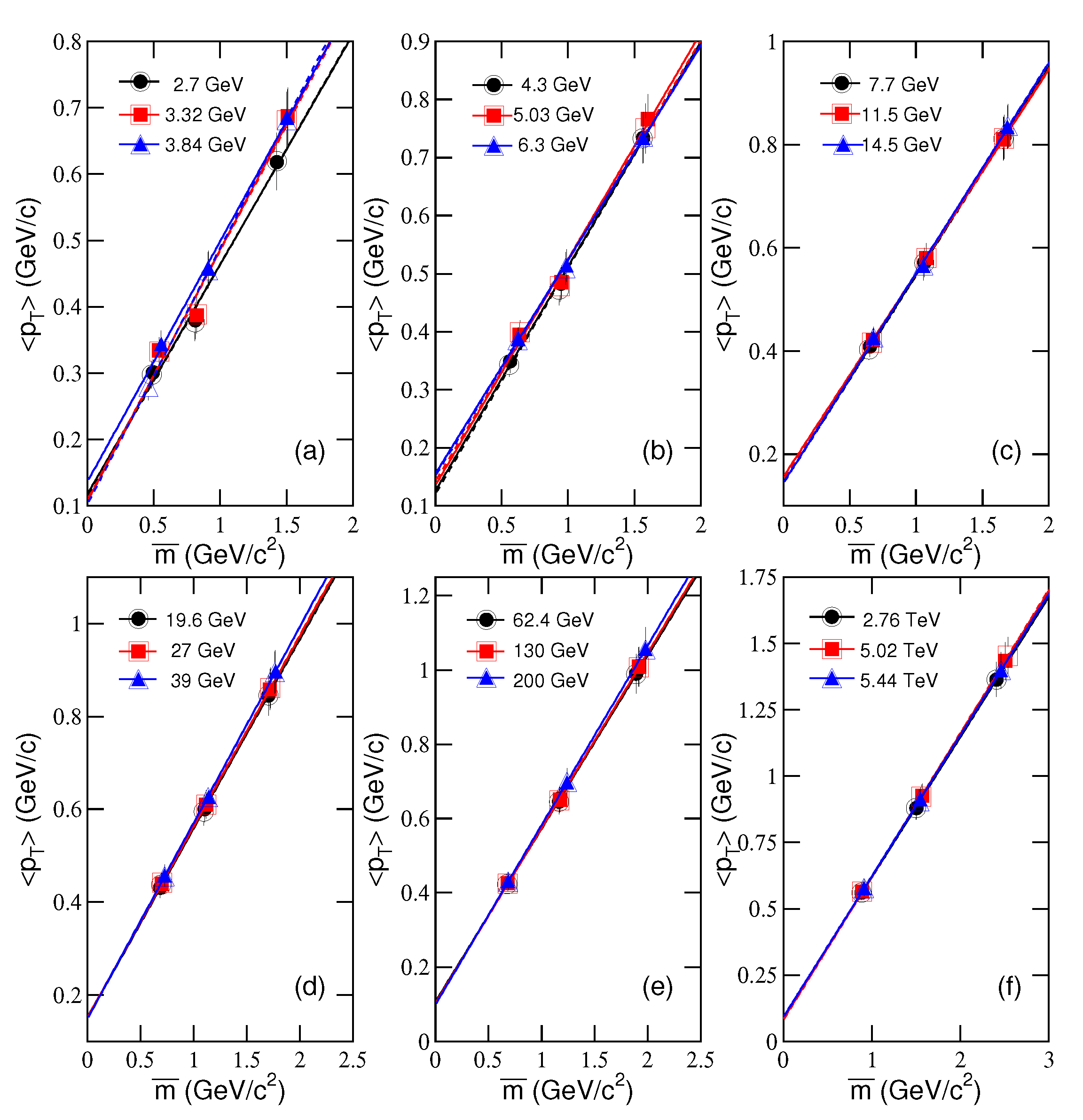
| Collab. | (GeV) | Particle | , (MeV) | q | /ndof | ||
|---|---|---|---|---|---|---|---|
| E866/E895 Au-Au | 2.7 | 11.87/19 | |||||
| 3.61/6 | |||||||
| p | 153.83/36 | ||||||
| 3.32 | 56.96/24 | ||||||
| 2.23/8 | |||||||
| p | 237.28/36 | ||||||
| 3.84 | 34.34/19 | ||||||
| 0.92/7 | |||||||
| p | 308.11/36 | ||||||
| 4.3 | 47.97/16 | ||||||
| 0.62/5 | |||||||
| p | 75.53/36 | ||||||
| E802 Au-Au | 5.03 | 129.94/30 | |||||
| 5.29/7 | |||||||
| p | 47.59/25 | ||||||
| NA49 Pb-Pb | 6.3 | 314.01/12 | |||||
| 41.92/6 | |||||||
| p | 6.99/10 | ||||||
| STAR Au-Au | 7.7 | 42.38/22 | |||||
| 3.02/16 | |||||||
| 0.95/11 | |||||||
| 11.5 | 44.84/22 | ||||||
| 1.07/19 | |||||||
| 1.38/19 | |||||||
| 14.5 | 4.09/24 | ||||||
| 0.84/14 | |||||||
| 0.28/21 | |||||||
| 19.6 | 32.66/21 | ||||||
| 19.01/22 | |||||||
| 2.20/18 | |||||||
| 27 | 27.71/21 | ||||||
| 10.49/20 | |||||||
| 4.56/18 | |||||||
| 39 | 35.77/22 | ||||||
| 9.02/22 | |||||||
| 1.64/18 | |||||||
| 62.4 | 103.95/6 | ||||||
| 1.50/6 | |||||||
| 5.98/11 | |||||||
| 130 | 122.72/6 | ||||||
| 2.23/8 | |||||||
| 20.75/8 | |||||||
| 200 | 85.21/7 | ||||||
| 0.42/6 | |||||||
| 27.56/12 | |||||||
| ALICE Pb-Pb | 2760 | 155.11/37 | |||||
| 4.63/32 | |||||||
| 22.39/38 | |||||||
| 5020 | 153.36/36 | ||||||
| 5.95/32 | |||||||
| 19.51/27 | |||||||
| ALICE Xe-Xe | 5440 | 21.89/36 | |||||
| 1.49/27 | |||||||
| 11.75/30 |
| Collab. | (GeV) | Particle | , (MeV) | q | /ndof | ||
|---|---|---|---|---|---|---|---|
| E866/E895 Au-Au | 2.7 | 12.31/19 | |||||
| 3.77/6 | |||||||
| p | 148.48/36 | ||||||
| 3.32 | 62.79/24 | ||||||
| 2.14/8 | |||||||
| p | 244.84/36 | ||||||
| 3.84 | 45.43/19 | ||||||
| 0.94/7 | |||||||
| p | 310.66/36 | ||||||
| 4.3 | 56.47/16 | ||||||
| 0.81/5 | |||||||
| p | 74.66/36 | ||||||
| E802 Au-Au | 5.03 | 164.90/30 | |||||
| 4.58/7 | |||||||
| p | 65.21/25 | ||||||
| NA49 Pb-Pb | 6.3 | 328.26/12 | |||||
| 30.95/6 | |||||||
| p | 6.79/10 | ||||||
| STAR Au-Au | 7.7 | 54.50/22 | |||||
| 1.90/16 | |||||||
| 1.33/11 | |||||||
| 11.5 | 41.38/22 | ||||||
| 1.03/19 | |||||||
| 1.36/19 | |||||||
| 14.5 | 3.74/24 | ||||||
| 0.81/14 | |||||||
| 0.30/21 | |||||||
| 19.6 | 39.67/21 | ||||||
| 17.06/22 | |||||||
| 2.27/18 | |||||||
| 27 | 27.36/21 | ||||||
| 10.01/20 | |||||||
| 4.67/18 | |||||||
| 39 | 59.05/22 | ||||||
| 9.05/22 | |||||||
| 1.65/18 | |||||||
| 62.4 | 97.82/6 | ||||||
| 1.50/6 | |||||||
| 16.62/11 | |||||||
| 130 | 143.34/6 | ||||||
| 2.25/8 | |||||||
| 19.97/8 | |||||||
| 200 | 111.25/7 | ||||||
| 0.42/6 | |||||||
| 28.32/12 | |||||||
| ALICE Pb-Pb | 2760 | 155.11/37 | |||||
| 4.64/32 | |||||||
| 22.50/38 | |||||||
| 5020 | 153.36/36 | ||||||
| 5.94/32 | |||||||
| 19.49/27 | |||||||
| ALICE Xe-Xe | 5440 | 21.89/36 | |||||
| 1.49/27 | |||||||
| 11.74/30 |
| Figure | Relation | System | (GeV) | Intercept | Slope | |
|---|---|---|---|---|---|---|
| Figure 5a | Au-Au | 2.7 | 1.08 | |||
| 3.32 | 4.50 | |||||
| 3.84 | 0.43 | |||||
| Figure 5b | Au-Au | 4.3 | 0.14 | |||
| 5.03 | 2.14 | |||||
| Pb-Pb | 6.3 | 0.24 | ||||
| Figure 5c | Au-Au | 7.7 | 0.48 | |||
| 11.5 | 0.36 | |||||
| 14.5 | 1.32 | |||||
| Figure 5d | Au-Au | 19.6 | 0.11 | |||
| 27 | 0.13 | |||||
| 39 | 0.18 | |||||
| Figure 5e | Au-Au | 62.4 | 0.01 | |||
| 130 | 0.03 | |||||
| Au-Au | 200 | 0.01 | ||||
| Figure 5f | Pb-Pb | 2760 | 0.45 | |||
| 5020 | 1.84 | |||||
| Xe-Xe | 5440 | 1.23 | ||||
| Figure 6a | Au-Au | 2.7 | 0.93 | |||
| 3.32 | 2.52 | |||||
| 3.84 | 0.22 | |||||
| Figure 6b | Au-Au | 4.3 | 0.17 | |||
| 5.03 | 0.94 | |||||
| Pb-Pb | 6.3 | 0.06 | ||||
| Figure 6c | Au-Au | 7.7 | 0.01 | |||
| 11.5 | 0.01 | |||||
| 14.5 | 0.16 | |||||
| Figure 6d | Au-Au | 19.6 | 0.01 | |||
| 27 | 0.01 | |||||
| 39 | 0.21 | |||||
| Figure 6e | Au-Au | 62.4 | 0.04 | |||
| 130 | 0.04 | |||||
| 200 | 0.01 | |||||
| Figure 6f | Pb-Pb | 2760 | 0.01 | |||
| 5020 | 0.01 | |||||
| Xe-Xe | 5440 | 0.01 |
| Figure | Relation | System | (GeV) | Intercept | Slope | |
|---|---|---|---|---|---|---|
| Figure 5a | Au-Au | 2.7 | 1.79 | |||
| 3.32 | 5.91 | |||||
| 3.84 | 0.48 | |||||
| Figure 5b | Au-Au | 4.3 | 0.45 | |||
| 5.03 | 3.10 | |||||
| Pb-Pb | 6.3 | 0.98 | ||||
| Figure 5c | Au-Au | 7.7 | 0.75 | |||
| 11.5 | 0.32 | |||||
| 14.5 | 1.37 | |||||
| Figure 5d | Au-Au | 19.6 | 0.15 | |||
| 27 | 0.14 | |||||
| 39 | 0.19 | |||||
| Figure 5e | Au-Au | 62.4 | 0.01 | |||
| 130 | 0.03 | |||||
| Au-Au | 200 | 0.01 | ||||
| Figure 5f | Pb-Pb | 2760 | 0.45 | |||
| 5020 | 1.84 | |||||
| Xe-Xe | 5440 | 1.23 | ||||
| Figure 6a | Au-Au | 2.7 | 0.99 | |||
| 3.32 | 2.31 | |||||
| 3.84 | 0.01 | |||||
| Figure 6b | Au-Au | 4.3 | 0.27 | |||
| 5.03 | 1.06 | |||||
| Pb-Pb | 6.3 | 0.10 | ||||
| Figure 6c | Au-Au | 7.7 | 0.01 | |||
| 11.5 | 0.01 | |||||
| 14.5 | 0.15 | |||||
| Figure 6d | Au-Au | 19.6 | 0.01 | |||
| 27 | 0.01 | |||||
| 39 | 0.79 | |||||
| Figure 6e | Au-Au | 62.4 | 0.03 | |||
| 130 | 0.04 | |||||
| 200 | 0.01 | |||||
| Figure 6f | Pb-Pb | 2760 | 0.01 | |||
| 5020 | 0.01 | |||||
| Xe-Xe | 5440 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.-L.; Liu, F.-H.; Olimov, K.K. Excitation Functions of Tsallis-Like Parameters in High-Energy Nucleus–Nucleus Collisions. Entropy 2021, 23, 478. https://doi.org/10.3390/e23040478
Li L-L, Liu F-H, Olimov KK. Excitation Functions of Tsallis-Like Parameters in High-Energy Nucleus–Nucleus Collisions. Entropy. 2021; 23(4):478. https://doi.org/10.3390/e23040478
Chicago/Turabian StyleLi, Li-Li, Fu-Hu Liu, and Khusniddin K. Olimov. 2021. "Excitation Functions of Tsallis-Like Parameters in High-Energy Nucleus–Nucleus Collisions" Entropy 23, no. 4: 478. https://doi.org/10.3390/e23040478
APA StyleLi, L.-L., Liu, F.-H., & Olimov, K. K. (2021). Excitation Functions of Tsallis-Like Parameters in High-Energy Nucleus–Nucleus Collisions. Entropy, 23(4), 478. https://doi.org/10.3390/e23040478








